A Divisia User Cost Interpretation of the Yield Spread Recession Prediction
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. The User Cost Spread and the Yield Spread
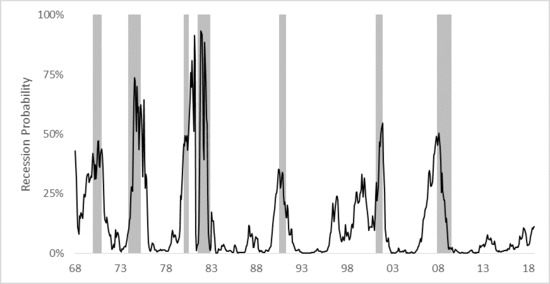
3.2. Empirical Results Using the User Cost Spread
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Code
References
- Andres, Javier, J. David Lopez-Salido, and Edward Nelson. 2004. Tobin’s Imperfect Asset Substitution in optimizing General Equilibrium. Journal of Money, Credit, and Banking 36: 665–90. [Google Scholar] [CrossRef]
- Barnett, William A. 1978. The User Cost of Money. Economics Letters 1: 145–49. [Google Scholar] [CrossRef]
- Barnett, William A. 1980. Economic Monetary Aggregates. Journal of Econometrics 14: 11–48. [Google Scholar] [CrossRef]
- Barnett, William A., and Apostolis Serletis. 2005. The Theory of Monetary Aggregation. North Holland: Elsevier, ISBN 0-444-50119-3. [Google Scholar]
- Barnett, William A., Jia Liu, Ryan S. Mattson, and Jeff van den Noort. 2012. The New CFS Divisia Monetary Aggregates: Design, Construction, and Data Sources. Open Economies Review 24: 125–45. [Google Scholar] [CrossRef]
- Belongia, Michael T., and Peter N. Ireland. 2012. Interest Rates and Money in the Measurement of Monetary Policy. Journal of Business and Economic Statistics 33: 255–69. [Google Scholar] [CrossRef]
- Canzoneri, Matthew B., Robert Cumby, Behzad Diba, and DavidLópez-Salido. 2011. The Role of Liquid Government Bonds in the Great Transformation of American Monetary Policy. Journal of Economic Dynamics and Control 35: 282–94. [Google Scholar] [CrossRef]
- Diewert, Walter E. 1974. Intertemporal Consumer Theory and the Demand for Durables. Journal of Econometrics 14: 11–48. [Google Scholar] [CrossRef]
- Estrella, Arturo, and Frederic S. Mishkin. 1996. The Yield Curve as a Predictor of US Recessions. Federal Resrve Bank of New York. Current Issues in Economics and Finance 2. [Google Scholar] [CrossRef]
- Estrella, Arturo, and Mary R. Trubin. 2006. The Yield Curve as a Leading Indicator: Some Practical Issues. Federal Reserve Bank of New York. Current Issues in Economics and Finance 12: 5. [Google Scholar]
- Harvey, Campbell R. 1988. The Real Term Structure and Consumption Growth. Journal of Financial Economics 22: 305–33. [Google Scholar] [CrossRef]
- Marzo, Massimiliano, and Paolo Zagaglia. 2018. Macroeconomic Stability in a Model with Bond Transaction Services. International Journal of Financial Studies 6: 27. [Google Scholar] [CrossRef]
- Mattson, Ryan S., and Victor J. Valcarcel. 2016. Compression in Monetary User Costs in the Aftermath of the Financial Crisis: Implications for the Divisia M4 Monetary Aggregate. Applied Economics Letters 23: 1294–300. [Google Scholar] [CrossRef]
- Offenbacher, Edward A., and Mayaan Kellerman. 2013. Divisia Monetary Aggregates for Israel: Background Note and Metadata. Jerusalem: Bank of Israel Research Department, Monetary/Finance Division. [Google Scholar]
- Tobin, James. 1969. A General Equilibrium Approach to Monetary Theory. Journal of Money Credit and Banking 1: 15–29. [Google Scholar] [CrossRef]
- Zagaglia, Paolo. 2013. Forecasting Long Term Interest Rates with a General Equilibrium Model of the Euro Area: What Role for Liquidity Services of Bonds? Asia Pacific Financial Markets 20: 383–430. [Google Scholar] [CrossRef]
| 1 | The CFS provides up to Divisia M4, which includes short term 3-month Treasury Bills with overnight repurchase agreements, commercial paper, and large denomination time deposits. |

| User Cost Spread Recession Probabilities | Dependent Variable: | |
|---|---|---|
| Probability of Recession | ||
| (1) | (2) | |
| Treasury Spread | ||
| User Cost Spread | ||
| Constant | ||
| McFadden Pseudo R | 0.3111 | 0.3163 |
| In Sample MAE | 0.1684 | 0.1678 |
| In Sample RMSE | 0.2908 | 0.2899 |
| Out of Sample MAE | 0.0430 | 0.0364 |
| Out of Sample RMSE | 0.0562 | 0.0494 |
| Observations | 609 | 609 |
| Log Likelihood | −167.046 | −165.776 |
| Akaike Inf. Crit. | 338.093 | 335.553 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mattson, R.S. A Divisia User Cost Interpretation of the Yield Spread Recession Prediction. J. Risk Financial Manag. 2019, 12, 7. https://doi.org/10.3390/jrfm12010007
Mattson RS. A Divisia User Cost Interpretation of the Yield Spread Recession Prediction. Journal of Risk and Financial Management. 2019; 12(1):7. https://doi.org/10.3390/jrfm12010007
Chicago/Turabian StyleMattson, Ryan S. 2019. "A Divisia User Cost Interpretation of the Yield Spread Recession Prediction" Journal of Risk and Financial Management 12, no. 1: 7. https://doi.org/10.3390/jrfm12010007
APA StyleMattson, R. S. (2019). A Divisia User Cost Interpretation of the Yield Spread Recession Prediction. Journal of Risk and Financial Management, 12(1), 7. https://doi.org/10.3390/jrfm12010007