Research and Application of Hybrid Forecasting Model Based on an Optimal Feature Selection System—A Case Study on Electrical Load Forecasting

Abstract

The process of modernizing smart grid prominently increases the complexity and uncertainty in scheduling and operation of power systems, and, in order to develop a more reliable, flexible, efficient and resilient grid, electrical load forecasting is not only an important key but is still a difficult and challenging task as well. In this paper, a short-term electrical load forecasting model, with a unit for feature learning named Pyramid System and recurrent neural networks, has been developed and it can effectively promote the stability and security of the power grid. Nine types of methods for feature learning are compared in this work to select the best one for learning target, and two criteria have been employed to evaluate the accuracy of the prediction intervals. Furthermore, an electrical load forecasting method based on recurrent neural networks has been formed to achieve the relational diagram of historical data, and, to be specific, the proposed techniques are applied to electrical load forecasting using the data collected from New South Wales, Australia. The simulation results show that the proposed hybrid models can not only satisfactorily approximate the actual value but they are also able to be effective tools in the planning of smart grids.

1. Introduction

Electrical Load (EL) forecasting is a fundamental and vital task for economically efficient operation and controlling of power systems [1,2,3,4,5]. It has often been employed for energy management, unit commitment and load dispatch [6,7,8,9,10,11,12,13,14]. The high accuracy of load forecasting guarantees the safe and stable operation of power systems [15,16,17]. Therefore, it is necessary to improve the reliability and the forecasting accuracy of smart grids [18,19,20]. Reliable EL forecasting is able to decrease energy consumption and reduce environmental pollution [21,22,23,24].

However, EL forecasting is difficult because the time series of EL are complex and non-linear with daily, weekly and annual cycles. It includes random components owing to fluctuation in the electricity usage of individual users, large industrial with irregular hours of operations, holidays and even sudden weather condition [25,26,27,28,29,30,31,32,33,34,35,36,37]. Furthermore, EL forecasting incorporating Very Short Term Load Forecasting (VSTLF), Short-Term Load Forecasting (STLF) and Long-Term Load Forecasting (LTLF) is very important to power system security and economy, especially in the electricity market [38,39]. VSTLF and STLF are both employed to set up necessary basis for dispatching the power grid. The VSTLF mainly focuses on the load forecasting within 1 h, and one of the most important purposes for VSTLF is to optimize the daily power generation plan; in addition, the VSTLF could be employed for cold stand-by and spinning reserve. In the meantime, both VSTLF and STLF could be used to adjust the plan for overhaul on power grid. Some papers have obtained good results for VSTLF [40,41,42,43,44], but it is still a difficult task to dispatch and manage the power gird. Furthermore, compared to VSTLF, the application of STLF is more extensive with even greater difficulty [45]. Therefore, improving the accuracy of STLF is one of the most important means to improve the management of power systems for forecasting the EL accurately can save valuable time to manage smart grid in advance before a significant variation [30,37].

It is obvious from the literature reviews that studies at EL forecasting still play a vital part in the electrical power system, which will have a great effect on its planning and operation. Therefore, it is very desirable to develop an EL forecasting model of higher accuracy. In order to achieve accurate and stable STLF, a large number of approaches have been employed, among which Statistical Methods (SM), Machine Learning Approaches (MLA) and Hybrid Approaches (HA) are the mainstream [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61].

The Statistical Methods (SM), such as Autoregressive Integrated Moving Average (ARIMA) and Auto Regressive Moving Average (ARMA), have good real-time performance when compared with other models [62,63,64]. In ARIMA, there is an additional parameter called differencing degree, which means the number of non-seasonal differences to fine tune the models to be more accurate on the basis of ARMA [65,66]. Feinberg and Eugene A [10] have employed fractional-ARIMA model to forecast the load at multiple time points over a time span between 1 and 24 h. Through comparing the proposed models with other methods, the experimental results showed that the hybrid model could improve the forecasting accuracy to a large degree. Steinherz and Pappas [67] evaluated the development of electricity markets through combining ARMA with GARCH (Generalized AutoRegressive Conditional Heteroskedasticity). These models were preferred for estimating load on electricity markets. Pappas et al. [68] presented a new method for electricity demand load forecasting with the multi-model partitioning theory and compared its effectiveness with three other well established time series analysis techniques, including Schwarz’s Bayesian Information Criterion (BIC), Akaike’s Information Criterion (AIC) and Corrected Akaike Information Criterion (AICC). The experimental results indicated that the proposed model had been effective in load forecasting. However, such methods cannot properly represent the complex nonlinear relationship between the load and a variety of stochastic factors such as hourly, daily, weekly and monthly time periodicity and social events that could cause unpredictable variations in power demand.

In view of the outstanding ability for nonlinear systems, ANNs have been extensively applied to STLF [69,70,71,72,73,74,75,76,77], and the different Artificial Neural Network (ANN) models, with and without load profiling, have been verified in previous studies. The neural network model had a multilayer perception architecture 5-5-1 with hyperbolic tangent function in the hidden layer and linear function in the output layer. The experiments showed that the coefficient of determination was above 0.9, which indicated the high effect of the model. Chaturvedi et al. [73] utilized a Generalized Neural Network (GNN) for the EL forecasting to overcome the drawbacks of ANN. GNN combined with fuzzy system and adaptive genetic algorithm was presented to be the most effective forecasting model. Lou and Dong [74] modeled fuzzy and random uncertainties of electric load forecasting based on the random fuzzy variables. Then a novel technique—Random Fuzzy Neural Network (RFNN) was obtained and the model was promising in micro grids and small power systems.

To improve the forecasting accuracy and stability, ANNs are often combined with other techniques, such as wavelet transforms, to build a hybrid model according to the characteristics of the functional system, as described in several articles [78,79,80,81,82,83]. Ghelardoni et al. [71] used Secondary Decomposition Algorithm (SDA) and the Support Vector Machine (SVM) to predict the load. In addition, the Fast Ensemble Empirical Mode Decomposition (FEEMD) and Wavelet Packet Decomposition (WPD) are applied to de-noise the original time series data, and then the final results demonstrated that the proposed methods are effective in load forecasting. Hong [84] presented an electric load forecasting model that combined the seasonal recurrent support vector regression model with chaotic artificial bee colony algorithm in order to reduce the forecasting errors. The final experimental results demonstrated that the model was a promising alternative for the forecasting of EL. Nie et al. [85] combined Support Vector Machine (SVM) and ARIMA to forecast the short-term EL. After testing the effectiveness of the model by a large sample, the results showed that the hybrid model was valid in the time series forecasting. Bahrami et al. [86] developed a new hybrid model based on the combination of Wavelet Transform (WT) and Grey Model (GM) to realize the short-term forecasting and the Particle Swarm Optimization (PSO) had been applied to optimize the model. The simulation results confirmed that the hybrid model had favorable performance for short-term EL forecasting compared with other models.

From the review above, it could be found that the hybrid forecasting models are more popular in time series forecasting, because they are more effective compared with the single models and can save the computational time. Besides, the feature learning of original data is useful in reducing the forecasting errors.

The primary purpose of this paper is to propose a hybrid neural network model (P-ENN-ARSR) to predict the EL based on pyramid system. Initially, the Pyramid Data Recognize System (PDRS) is designed as a Delay Calculation Operator (DCO) in P-ENN, which network is able to store the characteristics of a period of data. Then, the P-ENN with an Auto-Recurrence Spline Rolling model (ARSR) is utilized to short-term load forecasting (STLF). The results of the power consumption forecasting model have been tested by using the data of New South Wales, Australia. Furthermore, for evaluating the forecasting accuracy of load forecasting, we have developed a Forecasting Validity Degree (FVD) which could appraise the electrical load forecasting with effectiveness and reliability. In addition, in order to prove the effectiveness of the proposed hybrid model, three experiments are performed to examine the validity of EL prediction. The major contributions of this paper are as follows:

(1)

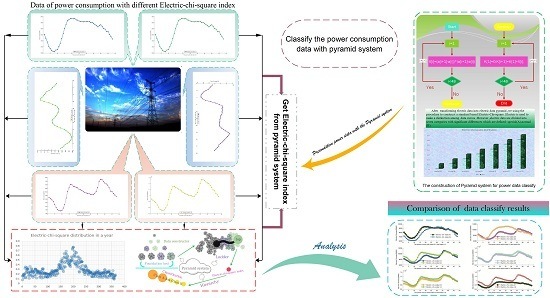
A new feature learning method called Pyramid Data Classification System, designed to recognize and store the features of original data, is built for recurrent neural networks to improve the forecasting accuracy.

(2)

A novel hybrid model incorporating ENN and ARSR, which is both an effective and simple tool, has been proposed to deal with the data with different features for performing the EL forecasting.

(3)

A new evaluation method has been formed, which is called improved forecasting validity degree (IFVD). It is developed according to its basic form of forecasting validity degree. This evaluation metrics is more sensitive to the trend change of the data and can identify the performance of the model more accurately.

The rest of this paper is organized as follows: Section 2 explains the methodology that is used in the research, and evaluation metrics of the model is presented in Section 3. Section 4 shows the three experimental results to prove the effectiveness of the hybrid model presented in this paper. Finally, Section 5 contains the conclusion.

2. Methodology

The hybrid model developed in this paper is based on the preprocessing of the original time series, Elman neural network model (ENN) and Auto-Recurrence Spline Rolling model (ARSR); therefore, this section introduces the two methods, respectively.

2.1. The Pyramid Data Classification System

The Pyramid data classification system used to preprocess the original data is developed based on an index of Electric-chi-square. When the original data have been input into the Pyramid system, both the short-term data and the long-term data could be considered as variations with time. The selection of a group of the data is placed in the bottom of a Pyramid. The top data are calculated by the underlying data, and the top floor of the data after conversion is called the Electric-chi-square index. Each term of the data will obtain its own index. According to the different indexes, the data series are divided into different categories.

Table 1. The structure of Pyramid data classification system.

Data
The value of the data is in each pyramid. The value is a double figure. A double value containing the total of the real load data on the previous record. A seasonal data series is put into the bottom of the pyramid.
Operations
Constructor
Initial values:	The value of the data to be measured.
Process:	Initialize the data value. Specify the figure of the data in each foundation bed of the pyramid.
Foundation bed
Input:	None
Preconditions:	None
Process:	Import the data and compute the variance of the adjacent data.
Output:	None
Postconditions:	None
Ladder
Input:	None
Preconditions:	None
Process:	Compute the figure sum of the variance in the foundation bed.
	Specify the average of the sum.
	Do multiply operation on the sum and the average.
Output:	Return the final result of each pyramid.
Postconditions:	None
Hierarchy
Input:	None
Preconditions:	None
Process:	Quote the list of the top values of the pyramid to compute the Electric-Chi-Square index.
	FVD the data based on the Electric-Chi-Square index.
Output:	None
Postconditions:	None

illustrates the structure of Pyramid data classification system and the pseudo code is listed below.

Remark 1.

The pyramid system is a developed type of feature learning method based on the data. Considering the features of the power consumption data, if the interval of the data sample is reduced to 10 min, then the effect of classification could be more obvious.

Algorithm: Pyramid System.

Input: $x^{\left(0\right)}=\left(x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(0\right)}\left(l\right)\right)$—a sequence of the sample data.

Output: ${\tilde{x}}^{\left(0\right)}=\left({\tilde{x}}^{\left(0\right)}\left(l+1\right),{\tilde{x}}^{\left(0\right)}\left(l+2\right),\cdots ,{\tilde{x}}^{\left(0\right)}\left(l+n\right)\right)$—a sequence of the forecasting data.

Parameters:

l—The number of sample data to build the Pyramid system in each rolling loop.

m—The number of forecasting data in each loop, namely n data to be forecasted in total.

$n$—An integer number which is called rolling number and $k=m$.

1: $R^s=\left(x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(0\right)}\left(l\right)\right)$/* it was able to set up before the program began*/

2: Build Pyramid/*a Pyramid system with the data set for feature learning */

3: While $\left(k<m\right)$ Do/* only on the first occasion has it ever been announced */

4: Calculate ${\tilde{R}}^m$/* A developed index of feature learning method based on the data */

${\tilde{R}}^m=\left(x^{\left(0\right)}\left(1+\left(k-1\right)m+1\right),x^{\left(0\right)}\left(1+\left(k-1\right)m+2\right),\cdots ,x^{\left(0\right)}\left(1+km\right)\right)$

${\tilde{x}}^{\left(0\right)}\left(l\right)=\left(x^{\left(0\right)}\left(l\right)-x^{\left(0\right)}\left(l-1\right)\right)\left(x^{\left(0\right)}\left(l\right)-x^{\left(0\right)}\left(l-1\right)\right)$

5: Fetch $R^s=\left(\frac{{\tilde{x}}_1^{\left(0\right)}+{\tilde{x}}_2^{\left(0\right)}}{2},\frac{{\tilde{x}}_1^{\left(0\right)}+{\tilde{x}}_2^{\left(0\right)}+{\tilde{x}}_3^{\left(0\right)}}{3},\cdots ,\frac{{\displaystyle \sum _{i=1}^{i-1}{\tilde{x}}_i^{\left(0\right)}}}{i-1}\right)$;

6: Rebuild $k=k+1$ /* reset the Pyramid system using the data set $R^s$ */

7: End Return ${\tilde{x}}^{\left(0\right)}=\left({\tilde{x}}^{\left(0\right)}\left(l+1\right),{\tilde{x}}^{\left(0\right)}\left(l+2\right),\cdots ,{\tilde{x}}^{\left(0\right)}\left(l+n\right)\right)$;

2.2. Elman Neural Network Model (ENN)

The ENNM is a type of network that is similar to a three-layer feed-forward neural network, and the network has a context layer that feeds back the hidden layer outputs in the previous steps and thereby the networks have somewhat memories. Furthermore, the neurons contained in each layer are used to propagate information from one layer to another.

2.2.1. Network Training Algorithm

This paper employs back propagation (BP) to train the network and the weight is a key parameter for BP to adjust the difference between actual output and expected output of the network.

Definition 1.

When the output of the network has an unacceptable difference from the expected output, the weights of the hidden layer and the output layer should be updated by the appropriate updating method as shown in Equation (1) [55].

$$△\mathit{w}\mathbf{\left(}\mathit{n}\mathbf{\right)}=\mathit{\eta }\mathbf{\left(}1-\mathit{\alpha }\mathbf{\right)}\frac{\mathbf{\partial }\mathit{E}}{\mathbf{\partial }\mathit{w}}+\mathit{\alpha }△\mathit{w}\mathbf{\left(}\mathit{n}-1\mathbf{\right)}$$

(1)

where $△\mathit{w}\mathbf{\left(}\mathit{n}\mathbf{\right)}$ denotes the weight of loop $\mathit{n}$, and $\mathit{\eta }$ denotes the learning rate of the network. The momentum factor is $\mathit{\alpha }$, and $\mathbf{\partial }\mathit{e}/\mathbf{\partial }\mathit{w}$ denotes the gradient direction of the weights.

2.2.2. Number of Network Neurons

To select proper number of hidden layer is a much complicated problem that there is no unified or ideal method. Its number is directly related to the final forecasting accuracy of the hybrid more. If the number is too small, it is difficult for the network to learn by using enough information; however, on the contrary, with too large number, the fault tolerance becomes lower and both the learning and training time will increase accordingly. Therefore, it is of great significance to apply suitable number of hidden layer to the forecasting.

The number of hidden layer is estimated in the range from five to twenty according to some empirical methods [87,88,89,90,91,92,93,94,95,96,97,98,99]. To select the best one in this range, an experiment is done based on the 1st–360th series of the original wind speed series. The dynamic change in hidden status neuron activation in the context layer is adjusted as Equation (2).

$${\mathit{S}}_{\mathit{i}}\mathbf{\left(}\mathit{t}\mathbf{\right)}=\mathit{g}\mathbf{\left(}{\displaystyle \mathbf{\sum }_{\mathit{k}=1}^{\mathit{k}}{\mathit{V}}_{\mathit{i}\mathit{k}}{\mathit{S}}_{\mathit{k}}\mathbf{\left(}\mathit{t}-1\mathbf{\right)}+{\displaystyle \mathbf{\sum }_{\mathit{j}=1}^{\mathit{J}}{\mathit{W}}_{\mathit{i}\mathit{j}}{\mathit{I}}_{\mathit{j}}\mathbf{\left(}\mathit{t}-1\mathbf{\right)}}}\mathbf{\right)}$$

(2)

where ${\mathit{S}}_{\mathit{k}}\mathbf{\left(}\mathit{t}-1\mathbf{\right)}$ and ${\mathit{I}}_{\mathit{j}}\mathbf{\left(}\mathit{t}-1\mathbf{\right)}$ denote the output of the context state and input neurons, respectively. ${\mathit{V}}_{\mathit{i}\mathit{k}}$ and ${\mathit{W}}_{\mathit{i}\mathit{j}}$ denote their corresponding weights, and $\mathit{g}\mathbf{\left(}\mathit{x}\mathbf{\right)}$ is a sigmoid transfer function.

Remark 2.

Table 2. Parameters and performance results of the developed neural networks for all the simulations.

Number of Hidden Layer	Results of One-Step Ahead Forecasting			Number of Hidden Layer	Results of One-Step Ahead Forecasting
	MAPE (%)	MAE (m/s)	MSE (104 m/s2)		MAPE (%)	MAE (m/s)	MSE (104 m/s2)
4	6.95	619.34	7.1127	10	7.01	629.35	7.0283
5	6.92	615.89	7.1183	11	6.77	606.52	6.2559
6	6.61	591.30	6.1117	12	6.80	609.64	6.4435
7	6.96	621.77	6.9602	13	6.70	600.17	6.1422
8	6.93	621.15	6.5277	14	6.63	592.31	6.0193
9	6.75	604.03	6.2331	15	6.74	605.14	6.3197

shows the performance results with different numbers of hidden layer, and it is clearly seen that the number is 6, the result is the best with the lowest MAPE of 6.61%, MAE of 591.30 and MSE of 6.1117. Therefore, the parameters of ENNM in this paper are set below:

♦ 

Number of input neurons: 4.

♦ 

Best number of hidden layer neurons: 6.

♦ 

Number of output neurons: 1.

♦ 

Value of the learning rate: 0.01.

♦ 

Number of iterations: 1000.

2.3. Auto-Recurrence Spline Rolling Model

This paper presents ARSR model to perform the forecasting through extracting information and establishing trend extrapolation model. This method can get over the drawbacks of grey model (GM) and obtain better forecasting accuracy [56]. The detailed meaning of single variable linear differential model and spline interpolation in this paper is explained below.

Definition 2.

The form of the single variable linear differential model is as follows:

$$\frac{{\mathit{d}}^{\mathit{m}}\mathit{y}}{\mathit{d}{\mathit{x}}^{\mathit{m}}}+{\mathit{a}}_1\frac{{\mathit{d}}^{\mathit{m}-1}\mathit{y}}{\mathit{d}{\mathit{x}}^{\mathit{m}-1}}+\cdots {\mathit{a}}_{\mathit{m}-1}\frac{{\mathit{d}}^1\mathit{y}}{\mathit{d}{\mathit{x}}^1}+{\mathit{a}}_{\mathit{m}}\mathit{y}+{\mathit{a}}_{\mathit{m}+1}=0\mathbf{\left(}\mathit{i}=1,2,\mathrm{...},\mathit{m}+1\mathbf{\right)}$$

(3)

The spline interpolation problem formulation could be described as follows (only given an odd spline function):

$$\mathbf{\left\{}\begin{array}{ll}\mathit{s}\mathbf{\left(}{\mathit{x}}_{\mathit{i}}\mathbf{\right)}={\mathit{y}}_{\mathit{i}}& \hfill \mathbf{\left(}\mathit{i}=1,2,\mathrm{...},\mathit{N}-1\mathbf{\right)}\\ {\mathit{s}}^{\mathbf{\left(}\mathit{a}\mathbf{\right)}}\mathbf{\left(}{\mathit{x}}_{\mathit{i}}\mathbf{\right)}={\mathit{y}}_{\mathit{i}}^{\mathbf{\left(}\mathit{a}\mathbf{\right)}}& \hfill \mathbf{\left(}\mathit{i}=0,\mathit{N};\mathit{a}=0,1,\mathrm{...},\mathit{n}-1\mathbf{\right)}\end{array}\mathbf{\right\}}$$

(4)

where $\mathbf{\left\{}{\mathit{x}}_{\mathit{i}}|\mathit{i}=0,1,\cdots ,\mathit{N}\mathbf{\right\}}$ are the nodes of interpolation, $\mathbf{\left\{}{\mathit{y}}_{\mathit{i}}|\mathit{i}=0,1,\cdots ,\mathit{N}\mathbf{\right\}}$ are the values of the nodes and $\mathbf{\left\{}{\mathit{y}}_{\mathit{i}}^{\mathbf{\left(}\mathit{a}\mathbf{\right)}}|\mathit{i}=0,1,\cdots ,\mathit{n}-1\mathbf{\right\}}$ are the interpolations of the nodes that the index is determined as (a).

Definition 3.

In Equation (8), s(x) is the k-order spline formula with the following form:

$$\mathit{s}\mathbf{\left(}\mathit{x}\mathbf{\right)}={\displaystyle \mathbf{\sum }_{\mathit{j}=0}^{\mathit{N}+\mathit{k}-1}{\mathit{C}}_{\mathit{j}-\mathit{m}+1}}{\mathit{\phi }}_{\mathit{j}-\mathit{m}+1,\mathit{k}}$$

(5)

where ${\mathit{\phi }}_{\mathit{j}-\mathit{m}+1,\mathit{k}}\mathbf{\left(}\mathit{x}\mathbf{\right)}={\mathit{N}}_{\mathit{k},\mathit{j}-\mathit{k}}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{\left(}\mathit{j}=0,1,\mathrm{...},\mathit{N}+\mathit{k}-1\mathbf{\right)}$.

Definition 4.

The B spline function has the following form

$$\mathbf{\left\{}{\mathit{N}}_{\mathit{k},\mathit{j}}\mathbf{\left(}\mathit{x}\mathbf{\right)},\mathit{j}=-\mathit{k},-\mathit{k}+1,\mathrm{...},\mathit{N}-1\mathbf{\right\}}$$

(6)

where ${\mathit{N}}_{\mathit{k},\mathit{j}}\mathbf{\left(}\mathit{x}\mathbf{\right)}=\mathbf{\left(}{\mathit{x}}_{\mathit{j}+\mathit{k}+1}-{\mathit{x}}_{\mathit{j}}\mathbf{\right)}{\mathit{G}}_{\mathit{k}}\mathbf{\left(}{\mathit{x}}_{\mathit{j}}-\mathit{x},\cdots ,{\mathit{x}}_{\mathit{j}+\mathit{k}+1}-\mathit{x}\mathbf{\right)}$ and ${\mathit{G}}_{\mathit{k}}\mathbf{\left(}\mathit{x}\mathbf{\right)}=\mathbf{\{}\begin{array}{ll}{\mathit{x}}_{\mathit{k}}& \mathbf{\left(}\mathit{x}\ge 0\mathbf{\right)}\\ 0& \mathbf{\left(}\mathbf{x}<0\mathbf{\right)}\end{array}$.

When the nodes spread equidistantly, suppose that ${\mathit{x}}_{\mathit{j}}={\mathit{x}}_0+\mathit{j}\mathit{h}$; in this case,

$${\mathit{N}}_{\mathit{k},\mathit{j}}\mathbf{\left(}\mathit{x}\mathbf{\right)}={\mathbf{\Omega }}_{\mathit{k}}\mathbf{\left(}\frac{\mathit{x}-{\mathit{x}}_0}{\mathit{h}}-\mathit{j}-\frac{\mathit{k}+1}{2}\mathbf{\right)}$$

(7)

Definition 5.

${\mathbf{\Omega }}_{\mathit{k}}\mathbf{\left(}\mathit{x}\mathbf{\right)}$ is defined as follows:

$${\mathbf{\Omega }}_{\mathit{k}}\mathbf{\left(}\mathit{k}\mathbf{\right)}={\displaystyle \mathbf{\sum }_{\mathit{j}=0}^{\mathit{k}+1}\frac{{\mathbf{\left(}-1\mathbf{\right)}}^{\mathit{j}}\mathbf{\left(}\begin{array}{l}\mathit{k}+1\\ \mathit{j}\end{array}\mathbf{\right)}{\mathbf{\left(}\mathit{x}+\frac{\mathit{k}+1}{2}-\mathit{j}\mathbf{\right)}}^{\mathit{k}}}{\mathit{k}\mathbf{!}}\mathbf{\left(}\mathit{k}=0,1,2,3,\cdots \mathbf{\right)}}$$

(8)

If the original discrete data are sufficiently smooth with a continuous process, the spline interpolation function defined by Equations (7) and (8) could describe the real process of the past well. However, as s(x) could not forecast the future, the s(x) should be put with the massive past information into the differential forecasting model. Then, s(x) could be put into Equation (6), and the differential equation could be obtained as follows:

$$\frac{{\mathit{d}}^{\mathit{m}}\mathit{s}\mathbf{\left(}\mathit{x}\mathbf{\right)}}{\mathit{d}{\mathit{x}}^{\mathit{m}}}+{\mathit{a}}_1\frac{{\mathit{d}}^{\mathit{m}-1}\mathit{s}\mathbf{\left(}\mathit{x}\mathbf{\right)}}{\mathit{d}{\mathit{x}}^{\mathit{m}-1}}+\cdots +{\mathit{a}}_{\mathit{m}-1}\mathit{S}\mathbf{\left(}\mathit{x}\mathbf{\right)}+{\mathit{a}}_{\mathit{m}+1}=0$$

(9)

The detailed process of identifying the parameters ${\mathit{a}}_1,{\mathit{a}}_2,\cdots ,{\mathit{a}}_{\mathit{m}+1}$ is specified in Ref. [56].

Remark 3.

There are two types of data sets in the spline model: the actual data and the forecasted data that are calculated according to the actual data of the initial calculation process. In ARSR model, the new measured value of the actual is used to replace the independent variable used in the spline model, which means that the procedure above would be updated by the actual data as a recurrence.

This method with small calculated amount and fast speed effectively avoids the influence of former error on the latter error; therefore, it can improve the forecasting accuracy.

2.4. The Hybrid Model

The flowchart of this paper is described in Figure 1. As the Figure 1 illustrates, this paper uses the absolute percentage error as the judgment index for presenting the forecasting performance of different power consumption forecasting models. To examine the forecasting accuracy of distribution of skewness and kurtosis, this article introduces the validity index to further compare the forecasting performance of different power consumption forecasting models. Validity is based on the Invalid degree element with K order forecasting relative error, and this paper will present the general discrete form of forecasting validity equivalence. Moreover, the detailed processes are given as follows:

• Step 1: Set the initial selected individual model set:

  $${\mathit{M}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}=\mathbf{\left\{}{\mathit{m}}_1^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},{\mathit{m}}_2^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},{\mathit{m}}_3^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}\mathbf{\right\}}$$

  (10)
  Set the initial selected data set:

  $${\mathit{S}}_{\mathit{i}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}=\mathbf{\left\{}{\mathit{s}}_1^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},{\mathit{s}}_2^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},{\mathit{s}}_3^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},\cdots ,{\mathit{s}}_{\mathit{n}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}\mathbf{\right\}}$$

  (11)
  Establish different forecasting models and the details have been shown in above sections.

  $${\mathit{S}}_{\mathit{t}}={\mathit{\varphi }}_1{\mathit{S}}_{\mathit{t}-1}+\cdots +{\mathit{\varphi }}_{\mathit{p}}{\mathit{S}}_{\mathit{t}-\mathit{p}}+{\mathit{\epsilon }}_{\mathit{t}}-{\mathit{\sigma }}_1{\mathit{\epsilon }}_{\mathit{t}-1}-\cdots -{\mathit{\sigma }}_{\mathit{q}}{\mathit{\epsilon }}_{\mathit{t}-\mathit{q}},\mathit{t}\in \mathit{Z}$$

  (12)

  $${\mathit{m}}_2^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}\mathbf{\left(}{\mathit{S}}_{\mathit{j}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}\mathbf{\right)}=\mathit{A}\mathit{R}\mathit{S}\mathit{R}\mathit{M}\mathbf{\left(}{\mathit{S}}_{\mathit{j}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},{\mathit{S}}_{\mathit{j}+1}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},\mathit{S}\mathit{M}\mathbf{\left(}{\mathit{S}}_{\mathit{j}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}},{\mathit{S}}_{\mathit{j}+1}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}\mathbf{\right)}\mathbf{\right)}$$

  (13)

  $${\mathit{m}}_2^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}\mathbf{\left(}{\mathit{S}}^{\mathit{j}}\mathbf{\right)}=\mathit{F}\mathbf{\left(}{\displaystyle \mathbf{\sum }_{\mathit{j}=1}^{\mathit{n}}{\mathit{W}}_{\mathit{i}\mathit{j}}{\mathit{I}}_{\mathit{j}}\mathbf{\left(}\mathit{t}-1\mathbf{\right)}}\mathbf{\right)}\mathbf{*}\mathit{I}\mathit{F}\mathbf{\left(}\mathit{g}\mathbf{\left(}{\displaystyle \mathbf{\sum }_{\mathit{k}=1}^{\tilde{\mathit{n}}}{\mathit{V}}_{\mathit{i}\mathit{k}}{\mathit{S}}_{\mathit{k}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}\mathbf{\left(}\mathit{t}-1\mathbf{\right)}}+{\displaystyle \mathbf{\sum }_{\mathit{k}=1}^{\tilde{\mathit{n}}}{\mathit{W}}_{\mathit{i}\mathit{j}}{\mathit{I}}_{\mathit{j}}\mathbf{\left(}\mathit{t}-1\mathbf{\right)}}\mathbf{\right)}\mathbf{\right)}$$

  (14)

  where IF is a two-value function with 0–1, which means that if and only if the value of IF is 1 could model 2 obtain the correct value.
• Step 2: Apply the pyramid data classification system to analyze the predictability of the original time series, which forms the prerequisite conditions for accurate forecasting. The Pyramid system can also extract the optimal information from the original data that is used as the input variables of the optimized forecasting models.

  $$\mathit{S}={\displaystyle {\mathbf{\int }}_{\mathit{a}}^{\mathit{b}}\mathbf{\left(}\mathit{i}+1\mathbf{\right)}\mathbf{\left(}\frac{{\displaystyle {\mathbf{\int }}_{\mathit{a}}^{\mathit{t}}\Vert {\mathit{S}}_{\mathit{j}}-{\mathit{S}}_{\mathit{j}+1}\Vert }\mathit{d}\mathit{j}}{{\displaystyle {\mathbf{\int }}_{\mathit{b}}^{\mathit{t}}\mathit{i}\mathbf{\left(}\mathit{i}-1\mathbf{\right)}\mathit{d}\mathit{i}}}\mathbf{\right)}\mathit{d}\mathit{i}}$$

  (15)

  $${\mathit{S}}_{\mathit{j}}^{\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}}={\displaystyle \mathbf{\sum }_{\mathit{i}=1}^{\mathit{n}-1}\frac{\mathbf{\left(}{\displaystyle \mathbf{\sum }_{\mathit{i}=1}^{\mathit{n}-1}\mathbf{\left(}{\mathit{S}}_{\mathit{j}}-{\mathit{S}}_{\mathit{j}+1}\mathbf{\right)}\mathbf{*}}\mathbf{\left(}{\mathit{S}}_{\mathit{j}}-{\mathit{S}}_{\mathit{j}+1}\mathbf{\right)}\mathbf{\right)}\mathbf{\left(}\mathit{i}+1\mathbf{\right)}}{{\displaystyle \mathbf{\sum }_{\mathit{i}=1}^{\mathit{n}-1}\mathit{i}\mathbf{\left(}\mathit{i}-1\mathbf{\right)}}}}$$

  (16)
• Step 3: Transfer the data that has been classified into ENN, ARSR and ENN-ARSR to conduct the forecast.

  $${\mathit{Y}}_{\mathit{j}}^{\mathit{k}}=\mathbf{\left\{}{\mathit{y}}_1,{\mathit{y}}_2,{\mathit{y}}_3,\cdots ,{\mathit{y}}_{\mathit{n}}\mathbf{\right\}}$$

  (17)

  $${\mathit{y}}_{\mathit{j}}=\mathit{A}\mathit{R}\mathit{S}\mathit{R}\mathit{M}\mathbf{\left(}{\mathit{m}}_1^{\mathit{i}}\mathbf{\left(}{\mathit{S}}_{\mathit{j}}^i\mathbf{\right)},{\mathit{m}}_2^{\mathit{i}}\mathbf{\left(}{\mathit{S}}_{\mathit{j}}^i\mathbf{\right)}\mathbf{\right)}$$

  (18)

  where k means the serial number of test data, and i means the value of the Electric-chi-square index.
• Step 4: Update the forecasts with the actual data.
• Step 5: Evaluate the forecasting models using FVD and GCD analysis.

  $$\overrightarrow{\mathit{H}}\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1,{\mathit{m}}_{\mathit{i}}^2\mathbf{\right)}=\mathit{S}\mathit{i}\mathit{g}\mathit{m}\mathit{o}\mathit{i}\mathit{d}\mathbf{\left(}\mathit{n}\mathbf{*}{\mathit{m}}_{\mathit{i}}^1\mathbf{\left(}1-\sqrt{{\mathit{m}}_{\mathit{i}}^1-{\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1\mathbf{\right)}}^2}\mathbf{\right)}-\mathit{F}\mathit{i}\mathit{x}\mathbf{\left(}\mathit{n}\mathbf{*}{\mathit{m}}_{\mathit{i}}^1\mathbf{\left(}1-\sqrt{{\mathit{m}}_{\mathit{i}}^1-{\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1\mathbf{\right)}}^2}\mathbf{\right)}\mathbf{\right)}\mathbf{\right)}$$

  (19)

  $$\mathit{\zeta }\mathbf{\left(}\mathit{L}\mathbf{\right)}=\mathit{M}\mathit{a}\mathit{x}\mathbf{\left(}\mathit{M}\mathit{a}\mathit{x}\mathbf{\left(}\frac{1}{\mathit{N}}{\displaystyle \sum _{\mathit{t}=1}^{\mathit{N}}\frac{\min \mathbf{\left(}\min \mathbf{\left(}\mathit{a}\mathit{b}\mathit{s}\mathbf{\left(}{\mathit{e}}_{\mathit{i}\mathit{t}}\mathbf{\right)}\mathbf{\right)}\mathbf{\right)}+\mathit{\rho }\max \mathbf{\left(}\max \mathbf{\left(}\mathit{a}\mathit{b}\mathit{s}\mathbf{\left(}{\mathit{e}}_{\mathit{i}\mathit{t}}\mathbf{\right)}\mathbf{\right)}\mathbf{\right)}}{{\displaystyle \mathbf{\sum }_{\mathit{i}=1}^{\mathit{m}}\mathit{a}\mathit{b}\mathit{s}\mathbf{\left(}{\mathit{e}}_{\mathit{i}\mathit{t}}\mathbf{\right)}}+\mathit{\rho }\max \mathbf{\left(}\max \mathbf{\left(}\mathit{a}\mathit{b}\mathit{s}\mathbf{\left(}{\mathit{e}}_{\mathit{i}\mathit{t}}\mathbf{\right)}\mathbf{\right)}\mathbf{\right)}}}\mathbf{\right)}\mathbf{\right)}$$

  (20)
• Step 6: Finally, based on the Electric-chi-square index of the Pyramid data classification system, the forecasting results propose the corresponding rules of the Electric-chi-square index and different forecasting methods.
• Step 7: Establish the forecasting system for application with the conclusion proposed in Section 6.

3. Model Evaluation

In this experiment, three generally adopted indexes are adopted to evaluate the experimental results, including MAPE, MAE and MSE, and their equations are listed as

Table 3. The Definition of Metrics.

Metric	Definition	Equation
MAE	The average absolute forecast error of n times forecast results	$\mathbf{MAE}=\frac{1}{N}{\displaystyle \sum _{n=1}^N\left|y_n-{\stackrel{\wedge }{y}}_n\right|}$ (21)
MSE	The average of the prediction error squares	$\mathbf{MSE}=\frac{1}{N}{{\displaystyle \sum _{n=1}^N\left(y_n-{\stackrel{\wedge }{y}}_n\right)}}^2$ (22)
MAPE	The average of absolute error	$\mathbf{MAPE}=\frac{1}{N}{\displaystyle \sum _{n=1}^N\left|\frac{y_n-{\stackrel{\wedge }{y}}_n}{y_n}\right|}\times 100\%$ (23)

:

In addition to the three evaluation metrics referred above, including MAPE, MAE and MSE, another metric is also used to assess the performance of the model, i.e., forecasting validity degree (FVD). The FVD has been developed to have a full evaluation of the model performance. It defines the normal forecasting validity, which is based on the Invalid degree element of the k-order forecasting fractional error [57]. Due to the dispersion of the time series, this section shows the equally general discrete form of validity, and the related definitions are listed below.

Definition 6.

When $\mathit{H}\mathbf{\left(}{\mathit{x}}_{\mathit{i}}\mathbf{\right)}={\mathit{x}}_{\mathit{i}}$ is a one-element continuous function, $\mathit{H}\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1\mathbf{\right)}={\mathit{m}}_{\mathit{i}}^1$ is the 1-order forecasting validity of the ith forecasting method; while $\mathit{H}\mathbf{\left(}{\mathit{x}}_{\mathit{i}}\mathbf{\right)}={\mathit{x}}_{\mathit{i}}\mathbf{\left(}1-\sqrt{\mathit{y}-{\mathit{x}}_{\mathit{i}}^2}\mathbf{\right)}$ is a two-element continuous function, $\mathit{H}\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1,{\mathit{m}}_{\mathit{i}}^2\mathbf{\right)}={\mathit{m}}_{\mathit{i}}^1\mathbf{\left(}1-\sqrt{{\mathit{m}}_{\mathit{i}}^2-{\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1\mathbf{\right)}}^2}\mathbf{\right)}$ is the FVD-2-order forecasting validity of the ith forecasting method.

Remark 4.

The 1-order forecasting validity index is the mathematical expectation of the forecasting accuracy series. When the difference between 1 and the standard deviation of the forecasting accuracy series multiplies its mathematical expectation, the FVD-2-order forecasting validity index is obtained. The smaller the 2-order forecasting validity index appears, the more effective the forecasting method is.

The FVD-2-order forecasting validity index could evaluate the effectiveness of some models that cannot be achieved only by MAPE. Based on that, this paper develops a novel concept of the forecasting validity index defined in Definition 7.

Definition 7.

$\mathit{H}\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1,{\mathit{m}}_{\mathit{i}}^2\mathbf{\right)}={\mathit{m}}_{\mathit{i}}^1\mathbf{\left(}1-\sqrt{{\mathit{m}}_{\mathit{i}}^2-{\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1\mathbf{\right)}}^2}\mathbf{\right)}$ is the FVD-2-order forecasting validity of the ith forecasting method. The FVD-3-order forecasting validity of the ith forecasting method is shown by Formula (20):

$$\overrightarrow{\mathit{H}}\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1,{\mathit{m}}_{\mathit{i}}^2\mathbf{\right)}=\frac{1}{1-\exp \mathbf{\left(}-\frac{{\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^1\mathbf{\right)}}^3+2{\mathbf{\left(}{\mathit{m}}_{\mathit{i}}^2\mathbf{\right)}}^{\frac{1}{2}}}{2\sqrt{{\mathit{m}}_{\mathit{i}}^2}}\mathbf{\right)}}$$

(21)

Remark 5.

One type of forecasting validity index is a more obvious index than the other if its index value is larger than the other and its monotonicity is more obvious than the other.

4. Experiment

This section includes three experiments that are aimed at comparing the hybrid model proposed with other single models and proving its effectiveness. The data sets and results of data preprocessing are also included in this section.

4.1. Data Sets

The hybrid model, P-ENN-ARSR, is tested by using the EL data provided by the National Electricity Market Management Company (NEMMCO) of New South Wales (NSW), Australia. The EL data were collected on a half hourly basis (48 data points per day) for the year of 2011. This paper selects the season S = 4 and period T = 48 and Figure 2 shows the general trend of data.

To evaluate the forecasting results of different models, the observation values of the EL in the first four days were used to assess the Elman Neural Network model parameters, and the remaining data were used for the validation of the model. The actual data are used in ARSR model. The data selection scheme is demonstrated in Figure 3.

4.2. Data Preprocessing

A suitable data preprocessing method could improve the forecasting results even when compared with the same model. It not only can significantly reduce the error caused by extreme data of experimental results but also can be suitable for the characteristics of the experimental model. At the same time, the data preprocessing method would not have an influence on the nature of the data themselves.

In the process of data classification, each term of data would obtain an exclusive Electric-chi-square index, and a period of EL data with two data points would obtain an Electric-chi-square index. From

Table 4. Forecasting error results (MAPE).

Class	Electric-Chi-Square	Forecasting Model
		ENN	ARSR
Normal	0.1	2.75%	1.99%
	0.2	3.56%	2.60%
	0.3	3.02%	2.44%
	0.4	3.02%	2.44%
	0.5	3.53%	3.08%
Special	0.6	3.00%	3.41%
	0.7	3.28%	3.56%
	0.8	3.21%	4.44%
	0.9	4.43%	4.75%
	1.0	3.62%	4.54%

, it can be determined that when the Electric-chi-square index of a data set is less than 0.6, ARSR performs better than ENN. When the Electric-chi-square index is greater than 0.6, the results forecasted by ENN will be better than those of ARSR. The details of the Pyramid data classification system are shown in Figure 4.

Remark 6.

There are some data of different classes based on the Electric-chi-square index with totally different errors in forecasting, though they are difficult to distinguish based upon the statistical dispersion. The data set is mainly divided into different classes by the pyramid system according to the Electric-chi-square index. In the cases above, it is obvious that the different types of data defined by the pyramid system have close mean and STDEV values. Data series can be divided into different categories more positively and accurately if the Pyramid system has been applied to classified data.

4.3. Experimental Setup

In order to testify the effectiveness of the proposed hybrid model, named as P-ENN-ARSR, this paper carries out two experiments, including Experiment I, Experiment II and Experiment III.

Experiment I initially compares the hybrid model with the single model of ENN and ARSR, respectively. The comparison between P-ENN-ARSR and ENN-ARSR can prove the classified effects of Pyramid data classification system. The data applied in Experiment I are the short-term EL data with 30-min intervals. The data sets are divided into four: spring, summer, autumn and winter. Experiment II is designed to prove the better performance of P-ENN-ARSR through comparing with other famous forecasting models, including auto regressive moving average (ARMA), autoregressive integrated moving average (ARIMA), back propagation neural network (BPNN), support vector machine (SVM) and adaptive network-based fuzzy inference system (ANFIS). The number of data applied in the experiment is large enough to support the construction of all the models referred above. Experiment III is aimed at testify the validity of FVD-3-order FVD proposed in this paper through comparing it with the FVD-2-order FVD. Three models, including ENN, ARSR and P-ENN-ARSR, are applied to make the comparison.

4.4. Experiment I

Experiment I is aimed at prove the effectiveness of each part in the hybrid model.

Table 5. The forecasting results of hybrid model in spring and summer.

Actual Time	Electric-Chi-Square	Methods				Actual Time	Electric-Chi-Square	Methods
		ARSR	ENN	ENN-ARSR	P-ENN-ARSR			ARSR	ENN	ENN-ARSR	P-ENN-ARSR
Spring						Summer
2:00:00	0.47	3.46%	2.29%	1.02%	2.29%	2:00:00	0.16	2.77%	5.88%	3.84%	2.77%
4:00:00	0.64	0.63%	0.55%	2.27%	0.55%	4:00:00	0.24	1.19%	6.17%	4.56%	1.19%
6:00:00	0.4	3.98%	4.98%	4.05%	3.98%	6:00:00	0.34	5.48%	4.56%	3.64%	4.56%
8:00:00	0.6	6.71%	9.60%	1.28%	6.71%	8:00:00	1.14	6.22%	3.44%	2.84%	3.44%
10:00:00	0.69	2.64%	3.23%	4.92%	2.64%	10:00:00	0.89	2.64%	7.65%	4.30%	2.64%
12:00:00	0.58	0.26%	6.57%	1.62%	0.26%	12:00:00	0.74	0.31%	6.41%	4.32%	0.31%
14:00:00	0.5	1.04%	10.95%	6.12%	1.04%	14:00:00	0.63	0.56%	6.72%	4.53%	0.56%
16:00:00	0.43	2.95%	8.60%	1.79%	2.95%	16:00:00	0.54	1.05%	6.67%	4.24%	1.05%
18:00:00	0.64	5.17%	5.04%	5.10%	5.04%	18:00:00	0.74	4.63%	5.64%	6.30%	4.63%
20:00:00	0.58	1.15%	2.10%	1.26%	1.15%	20:00:00	0.67	0.35%	4.42%	1.39%	0.35%
22:00:00	0.54	2.35%	0.17%	1.92%	0.17%	22:00:00	0.66	4.18%	7.10%	4.73%	4.18%
00:00:00	0.51	3.80%	1.05%	0.61%	1.05%	00:00:00	0.63	1.52%	7.83%	1.57%	1.52%
MAE		4953.503	4739.778	1911.145	3204.385	MAE		2971.062	1138.262	2970.035	885.6493
MSE		899.5068	1117.057	1362.925	6786.523	MSE		549.7415	8507.127	5605.595	9296.089
MAPE		2.85%	4.59%	2.66%	2.32%	MAPE		2.58%	6.04%	3.85%	2.27%
FVD		0.8297	0.8625	0.8935	0.9722	FVD		0.7991	0.7545	0.8617	0.9635
IFVD		0.8569	0.7385	0.8820	0.9711	IFVD		0.8348	0.7440	0.8604	0.8168

and

Table 6. The forecasting results of hybrid model in autumn and winter.

Actual Time	Electric-Chi-Square	Methods				Actual Time	Electric-Chi-Square	Methods
		ARSR	ENN	ENN-ARSR	P-ENN-ARSR			ARSR	ENN	ENN-ARSR	P-ENN-ARSR
Autumn						Winter
2:00:00	0.23	2.53%	3.26%	0.80%	2.53%	2:00:00	0.2	2.89%	13.44%	4.09%	2.89%
4:00:00	0.54	0.17%	3.41%	4.05%	0.17%	4:00:00	0.5	0.40%	14.76%	3.88%	0.40%
6:00:00	0.55	7.67%	2.10%	3.00%	2.10%	6:00:00	0.54	7.43%	31.37%	3.60%	7.43%
8:00:00	1.85	4.93%	5.40%	3.06%	4.93%	8:00:00	1.7	4.04%	3.69%	5.80%	4.04%
10:00:00	1.48	2.89%	0.45%	4.41%	0.45%	10:00:00	1.35	3.76%	3.09%	1.77%	1.76%
12:00:00	1.26	1.30%	4.10%	5.14%	1.30%	12:00:00	1.14	0.92%	2.73%	2.12%	0.92%
14:00:00	1.08	0.24%	6.77%	2.33%	0.24%	14:00:00	0.97	0.04%	4.92%	0.79%	0.04%
16:00:00	0.94	3.84%	3.79%	4.41%	3.79%	16:00:00	0.84	2.39%	2.12%	6.27%	2.39%
18:00:00	1.18	6.74%	2.59%	2.77%	2.59%	18:00:00	1.17	7.02%	3.16%	4.30%	7.02%
20:00:00	1.07	1.10%	0.29%	5.61%	0.29%	20:00:00	1.06	1.51%	2.77%	3.20%	1.51%
22:00:00	1.05	5.37%	2.26%	5.55%	2.26%	22:00:00	1.05	6.07%	5.04%	4.26%	6.07%
00:00:00	1.02	1.47%	3.78%	1.71%	1.47%	00:00:00	1.02	2.76%	3.77%	3.63%	2.76%
MAE		4180.003	3496.746	4892.383	5274.083	MAE		5939.701	3166.08	2877.14	4808.086
MSE		9889.116	5223.754	8654.386	6125.665	MSE		2278.429	4980.943	9008.525	5746.612
MAPE		3.19%	3.18%	3.57%	1.84%	MAPE		3.27%	7.57%	3.64%	3.10%
FVD		0.7991	0.7545	0.8617	0.9635	FVD		0.8836	0.8062	0.8147	0.9129
IFVD		0.8348	0.7440	0.8604	0.8168	IFVD		0.8190	0.8961	0.8836	0.8883

show the comparison and construct of ARSR, ENN, ENN-ARSR and P-ENN-ARSR in different seasons. From the two tables, it could be seen that;

(1)

For spring and summer, the hybrid model P-ENN-ARSR has the best forecasting results at 9 and 10 points, respectively and ENN-ARSR achieves the highest forecasting accuracy at 3 and 2 points, respectively. Although P-ENN-ARSR does not have the best MAE or MSE, the hybrid model outperform other models in the aspect of MAPE, FVD and IFVD.

(2)

For autumn, in addition to the time of 6:00 am and 8:00 am, P-ENN-ARSR has the best forecasting performance when compared with other models. Similarly, for the time series in winter seven points are forecasted accurately using the hybrid model P-ENN-ARSR. In comparison of MAE, MSE, MAPE, FVD and IFVD, P-ENN-ARSR has the lowest forecasting errors.

Remark 7.

The reason for the results above is that in the hybrid model P-ENN-ARSR, the pyramid data classification plays an effective part in promoting the forecasting capacity of the ARSR and ENN models. The pyramid data classification system decreases the jumping character of the original EL data, and the system selects the initial weights and thresholds for building ARSR-ENN; therefore, the optimized ARSR-ENN can achieve forecasting with higher precision.

4.5. Experiment II

Experiment II is designed to compare the proposed hybrid model in this paper with other well-known forecasting models, including ARIMA, SVM, BPNN and ANFIS, to testify to its effectiveness. From

Table 7. Results of P-ENN-ARSR for EL forecasting at 5-h intervals.

Electric-Chi-Square	P-ENN-ARSR
	MAE	MSE	MAPE	FVD	IFVD
0.1	1.58 × 104	4.39 × 106	0.02	0.75	0.76
0.2	3.51 × 104	2.20 × 107	0.05	1.00	0.95
0.3	2.37 × 104	1.04 × 107	0.03	0.80	0.93
0.4	3.53 × 104	2.32 × 107	0.04	0.78	0.96
0.5	2.73 × 104	1.33 × 107	0.03	0.77	0.96
0.6	2.03 × 104	7.20 × 106	0.02	0.98	0.77
0.7	2.64 × 104	1.30 × 107	0.03	0.89	0.85
0.8	4.16 × 104	3.16 × 107	0.05	0.93	0.86
0.9	1.73 × 104	5.94 × 106	0.02	0.79	0.96
1	3.07 × 104	1.66 × 107	0.04	0.89	0.78

and

Table 8. Results of different models for EL forecasting at 5-h intervals.

Electric-Chi-Square	ARIMA					SVM
	MAE	MSE	MAPE	FVD	IFVD	MAE	MSE	MAPE	FVD	IFVD
0.1	8.26 × 103	1.06 × 107	0.04	0.93	0.86	7.12 × 103	6.95 × 106	0.03	0.99	0.90
0.2	7.80 × 103	1.05 × 107	0.02	0.79	0.86	7.02 × 103	8.44 × 106	0.02	0.76	0.94
0.3	7.52 × 103	8.03 × 106	0.01	0.99	0.91	1.23 × 104	2.46 × 107	0.08	0.75	0.89
0.4	1.36 × 104	3.53 × 107	0.13	0.76	0.87	1.17 × 104	2.31 × 107	0.08	0.87	0.97
0.5	8.51 × 103	1.30 × 107	0.02	0.81	0.84	1.14 × 104	2.07 × 107	0.08	0.87	0.97
0.6	1.30 × 104	3.68 × 107	0.12	0.87	0.82	1.23 × 104	2.70 × 107	0.11	0.91	0.75
0.7	1.47 × 104	3.74 × 107	0.11	0.85	0.90	9.29 × 103	1.45 × 107	0.05	0.76	0.75
0.8	1.37 × 104	2.91 × 107	0.10	0.94	0.90	9.48 × 103	1.44 × 107	0.03	0.90	0.85
0.9	1.40 × 104	3.59 × 107	0.05	0.88	0.74	1.11 × 104	1.96 × 107	0.05	0.97	0.98
1	1.09 × 104	2.04 × 107	0.05	0.75	0.99	1.03 × 104	1.67 × 107	0.04	0.79	0.94
Electric-Chi-Square	BPNN					ANFIS
	MAE	MSE	MAPE	FVD	IFVD	MAE	MSE	MAPE	FVD	IFVD
1	1.09 × 104	2.04 × 107	0.05	0.75	0.99	1.03 × 104	1.67 × 107	0.04	0.79	0.94
0.1	7.86 × 103	1.05 × 107	0.03	0.92	0.80	1.04 × 104	1.72 × 107	0.08	0.92	0.76
0.2	9.52 × 103	1.28 × 107	0.05	0.80	0.87	9.72 × 103	1.65 × 107	0.06	0.88	0.89
0.3	8.72 × 103	1.18 × 107	0.03	0.95	0.89	8.69 × 103	1.17 × 107	0.04	0.94	0.95
0.4	1.15 × 104	1.71 × 107	0.07	0.82	0.88	1.16 × 104	2.02 × 107	0.07	0.78	0.76
0.5	9.70 × 103	1.43 × 107	0.04	0.95	0.92	5.77 × 103	5.44 × 106	0.01	0.95	0.74
0.6	1.08 × 104	1.72 × 107	0.05	0.90	0.87	1.27 × 104	2.68 × 107	0.10	0.94	0.88
0.7	1.09 × 104	2.19 × 107	0.03	0.84	0.87	1.04 × 104	1.68 × 107	0.04	0.96	0.97
0.8	1.44 × 104	3.42 × 107	0.06	0.79	0.78	7.84 × 103	9.68 × 106	0.01	0.94	0.93
0.9	1.17 × 104	2.25 × 107	0.07	0.98	0.79	9.91 × 103	1.44 × 107	0.04	0.89	0.89
1	1.43 × 104	3.29 × 107	0.10	0.76	0.83	1.02 × 104	1.76 × 107	0.04	0.92	0.84

and Figure 5, the results can be summarized as:

(1)

The electric-Chi-Square ranges from 0.1 to 1, and it is clear that P-ENN-ARSR achieves the best MAPE at 5 points when compared with other models. Then, if evaluated by IFVD, the hybrid model proposed achieves the best values at 4 points separately. However, only when the electric-Chi-square is 0.2, P-ENN-ARSR has the highest FVD with the value of 0.9988.

(2)

ARIMA belongs to statistical models that are based on a large amount of historical information. SVM is the machine-based forecasting method that is suitable in the STLF. BPNN and ANFIS are both ANNs with strong ability of self-learning and self-adaption. These single models can outperform other ones at certain points; however, the overall forecasting performance of P-ENN-ARSR is the most excellent.

(3)

When electric-Chi-square is 0.4, 0.7, 0.8 and 0.9, FVD and IFVD have the similar evaluations results at the model of SVM and ANFIS. In comparison, IFVD has better ability to identify the right trend of the model.

Remark 8.

The hybrid mode combines ANN with statistical models, which takes the advantage of both the single ENN and ARSR. By conducting the experiment, we can conclude that the model is applicable in conducting the forecasting for EL time series. Moreover, the data applied in Experiment II are EL data with 5-h intervals and the forecasting accuracy is still low and in an acceptable scale; therefore, it is proved that the hybrid model P-ENN-ARSR is effective for STLF.

4.6. Experiment III

Experiment III compares the results of FVD-2-order and FVD-3-order forecasting validity index and from

Table 9. FVD-2-order and FVD-3-order index analysis.

Electric-Chi-Square	FVD-2-Order Index			Electric-Chi-Square	FVD-3-Order Index
	ENN	ARSR	P-ENN-ARSR		ENN	ARSR	P-ENN-ARSR
0.1	0.9051	0.8837	0.9175	0.1	1.63	1.61	1.58
0.2	0.8441	0.8406	0.8587	0.2	1.69	1.66	1.62
0.3	0.8360	0.8353	0.8482	0.3	1.68	1.65	1.62
0.4	0.7885	0.8328	0.8662	0.4	2.00	1.67	1.66
0.5	0.8231	0.8277	0.8345	0.5	1.70	1.68	1.65
0.6	0.7503	0.8158	0.8096	0.6	2.13	1.70	1.72
0.7	0.8162	0.8131	0.8222	0.7	1.70	1.70	1.67
0.8	0.8231	0.8121	0.8270	0.8	1.66	1.71	1.64
0.9	0.7601	0.8146	0.8123	0.9	1.70	2.09	1.71
1	0.7392	0.7932	0.8107	1	1.75	2.13	1.71

it can be concluded that:

(1)

For FVD-2-order forecasting validity index, ARSR has better forecasting performance than ENN when the index belongs to (0, 0.6). The single ENN performs better than the single ARSR within the index range of (0.7, 1). Among all the proposed models, the hybrid P-ENN-ARSR model has the best performance in the FVD-2-order forecasting validity.

(2)

For FVD-3-order forecasting validity index, when comparing the single ARSR and the single ENN, the former model has better forecasting performance than the latter while the indexes belong to (0, 0.5). ARSR achieves better performance than ENN when the index belongs to (0.6, 1). Among all the proposed models, the hybrid P-ENN-ARSR model has the best performance in the FVD-3-order forecasting validity.

(3)

When comparing the FVD-3-order forecasting validity indexes with the FVD-2-order forecasting validity indexes, it could be known that the former has much larger differences than the latter. For example, the FVD-2-order forecasting validity index with 0.4 of ENN, ARSR and P-ENN-ARSR is 0.7885, 0.8328 and 0.8662, respectively. The FVD-3-order forecasting validity index with 0.4 of ENN, ARSR and P-ENN-ARSR is 2.0, 1.67 and 1.66, respectively.

Remark 9.

While the Electric-chi-index belongs to 0.1–0.5, ARSR has more effective forecasting results than ENN. ENN performs better than ARSR when the Electric-chi-index is in the range of 0.6–1. While the Electric-chi-index belongs to 0.1–1, P-ENN-ARSR has more effective forecasting results than both ENN and ARSR. As we mentioned in Section 3, the FVD-3-order has better performance in evaluating forecasts than FVD-2-order.

5. Discussion

In this section, the factors of the forecasting models and PDRS have been discussed for promoting the forecasting performance. Meanwhile, the performance and the effect of train-test ratio not only have been tested but have been generated as well. Furthermore, two of the most important evaluation metrics, convergence speed and degree of certainty, have been presented and discussed in this section.

5.1. Forecasting Models

A great many of techniques for power system load forecasting have been proposed in the last decades [71,72,73,74,75,76,77,78,79,80,81]. Traditional forecasting approaches, such as ARMA and ARIMA, cannot give sufficiently accurate results. Conversely, complex algorithmic methods with heavy computational burden are able to converge slowly and may diverge in certain cases. As the literature reviews mentioned, a number of algorithms have been suggested for the load forecasting problem. Previous approaches can be generally classified into two types of categories in accordance with methods they employ. The first type of models have treated the load pattern as a time series signal and predicts the future load by using various time series analysis techniques. The second type of models have recognized that the load pattern is heavily dependent on features of electrical system, and finds a functional relation between the employed features and electrical load. The future load is then predicted by inserting the predicted information of electrical system into the predetermined functional relationship. In this paper a hybrid model which combines both time series and regression approaches has been presented, and the model not only has the advantage of fast computing speed, but is easy to implement as well.

5.1.1. Arguments of ARIMA

Based on the results of our experiments, ARIMA, which is better than two linear models, AR and ARMA. The reason for the unfavorable result produced by ARMA is that the ARMA could not fit the non-linear data series and it has a definite rhythmic pattern of fluctuations; however, all time series in data sets are not very regular so the irregular information has been removed entirely by the moving-average method. However, there is an additional parameter called differencing degree in ARIMA, which indicates the number of non-seasonal differences to fine tune the models to be more accurate on the basis of ARMA. Though the parameters could be facilitated by evaluating the partial autocorrelation functions for an estimate of p, it is still a difficult task to draw appropriate values of the arguments p and q in the AR, ARIMA and ARIMA. These models can be developed by least squares regression to generate the values of the parameters, which the parameters with the minor error have been chosen.

In our experiment, for Electrical Load, ARIMA (2, 4, 1) has obtained the best performances. In addition, we also tried other groups of p, q and d. The fitting performance improved gradually until d = 4, but when d is set to 4, the forecasting performance of the sample data of EL is not sufficient for fitting more parameters required in ARIMA. On the other hand, the forecasting performance is getting worse when q is larger than 1. Furthermore, the forecasting performances of ARIMA models are not only very dependent on their orders, but supported on the number of input sample data as well. We also observed that the models have good prediction accuracy at the first two points, but often poorly perform at the rest. It indicates that the proposed models are usually more suitable for STLF.

5.1.2. Analysis on Structures of Elman Networks

Our algorithm uses features of electrical load for modeling, and the ENN is able to perform non-linear modeling and adaptation. The proposed ENN are used for nonlinear forecasting have gained enormous popularity and success in EL forecasting because there is now a growing evidence that EL time series contain nonlinearities. As we expected, Elman outperforms most of other models shown in Table 6. However, there are many parameters required to be elaborately configured. However, there were no established rules for choosing the appropriate values of these parameters on EL forecasting. We had to resort to trial to obtain their appropriate values that lead to the best forecasting performance. Although there were many studies on how to tune the parameters of ENN, clearly, selection over the whole space of the parameters is beyond the scope of this article.

The different configurations of the three key parameters have been examined, including of train-test ratio, feedback delays, and hidden layers for EL. In addition, the ENN is a kind of neural networks with sharing the recurrent information in sample space. Thus, it is difficult to find a rule for updating parameters of ENN, and it is also challenging to find an appropriate strategy for updating parameters to bring the model to the best performance in the practical EL forecasting where the test data are unknown. During our experiment on ENN, we have tested the networks 100 times for each configuration with the same parameter setting and the forecasting values with the best performance by NN (the best is shown in Table 6) have been selected to compare with other models in Experiment II. Besides, general problems with the networks include the inaccuracy of prediction and numerical instability. One of the reasons this method often gives volatile results is that there is mechanism of randomness and probability inside the NN training methods. Another common criticism of ENNs is that they require an enormous amount of data for training in real-world operation. The training data of ENN are different with BP for the additional time-step in recurrent neural networks. The dimension of input data of ENNs is at least three, if the data have much more information, the dimensions of input will increase.

5.2. Trade-Off Based on PDRS

Note that it is an accepted fact that any of the modern Machine Learning algorithms will outperform traditional EL forecasts. A great many feed forward neural networks are used to forecast EL time series, but the feedforward neural network relies on the data features. It used local recognize to connect the different vectors into a lager vector and the last vector must be fix length. If we want to get better forecasting performance, the networks need to use a better feature learning methods. The natural method is used the larger vector as input data, but, when the dimension of input data increase, the weight matrix of ENN would be increasing rapidly. For example, if the dimension of input data and neurons both are 39, the dimension of weight matrix of the first layer will be 1521. Among which many weights are redundant, but they have to be computed in every iteration.

In this paper, we have employed the Pyramid Data Recognize System (PDRS) to reduce the amount of calculation in weight matrix in ENN and we discuss the factors related to the PDRS that would influence the trade-off of fitting and forecasting. We also test the performance of the effect of cross-validity sets in the training process and the different types of P-ENN are shown as

Table 10. The different types of P-ENN.

Experiment No.	Inference Type	Iterations in P-ENN	Nodes in Context Layer
1	P-ENN-I	5	6
2	P-ENN-I	5	12
3	P-ENN-I	5	18
4	P-ENN-II	10	6
5	P-ENN-II	10	12
6	P-ENN-II	10	18
7	P-ENN-III	15	6
8	P-ENN-III	15	12
9	P-ENN-III	15	18

.

5.2.1. Analysis of Fitting Performance

Thus far, in this paper, we have mainly focused on feature learning of PDRS. PDRS is not only relatively simple to recognize, but also has advantages over other approaches in terms of memory. However, PDRS has significant limitations in terms of fitting performance. This is because the linearity assumption is almost always a poor approximation. Table 10 presents three types of P-ENN which of different nodes in context layer, and the fitting accuracy are presented in

Table 11. The fitting performance evaluated by FVD of 3-order.

No.	PDRS-ENN-I	PDRS-ENN-II	PDRS-ENN-III	ANFIS	SVM	BPNN
1	1.60	1.60	1.61	1.91	1.88	1.73
2	1.61	1.59	1.61	1.92	1.90	1.75
3	1.60	1.58	1.59	1.90	1.90	1.72
4	1.62	1.59	1.63	1.90	1.86	1.72
5	1.61	1.60	1.60	1.93	1.88	1.73
6	1.62	1.59	1.62	1.92	1.87	1.73
7	1.58	1.58	1.61	1.92	1.90	1.71
8	1.60	1.60	1.59	1.90	1.86	1.74
9	1.61	1.61	1.61	1.89	1.87	1.75
Mean	1.61	1.60	1.61	1.91	1.88	1.73

. The cross-validity method is employed in this experiment.

The results represented by Table 11 show that the PDRS-ENNs have the better performance in fitting than other models and the PDRS-ENN-I has the best performance in fitting in all of models. The results also indicate that the memory unit of PDRS has good performance in feature learning. In PDRS, after the data had been got in the unit, the PDRS would generate the features of fitter data, and then the features would be connected by networks, the signals would be transform by the neurons. If the same features are transformed into the PDRS again, the neurons will be activated by the connections. Thus, the internal neurons of PDRS represent the features of data, or we can see that the internal neurons store the features of the data.

5.2.2. Analysis of Forecasting Performance

However, from

Table 12. The forecasting performance evaluated by FVD of 3-order.

No.	PDRS-ENN-I	PDRS-ENN-II	PDRS-ENN-III	ANFIS	SVM	BPNN
1	1.77	1.81	1.90	2.03	2.04	2.03
2	1.79	1.83	1.88	2.05	2.05	2.01
3	1.76	1.81	1.92	2.05	2.02	2.05
4	1.79	1.81	1.92	2.01	2.04	2.05
5	1.78	1.83	1.91	2.01	2.06	2.05
6	1.78	1.82	1.91	2.02	2.05	2.01
7	1.78	1.79	1.89	2.01	2.02	2.05
8	1.78	1.80	1.92	2.01	2.04	2.02
9	1.78	1.82	1.89	2.04	2.05	2.01
Mean	1.78	1.81	1.90	2.03	2.04	2.03

, we can see that the forecasting performance of PDRS-ENN-I is much better than others, the result further illustrates that the PDRS-ENN-I not only has excellent fitting capability but has good forecasting results as well. In addition, the cross-validity method is employed in this experiment.

This section presents the results of testing by using the PDRS-based forecasting algorithm. Table 12 describes the forecasting performance of PDRS-ENN-1, PDRS-ENN-II, PDRS-ENN-1II, ANFIS, SVM and BPNN in numerical experiments. The PDRS is constructed using the rules that are described in Section 2, which stimulates the prior influence of the EL in the numerical method. We have totally conducted nine experiments, which are based on cross-validity method. From Table 12, it can be known that PDRS-ENN-1 and PDRS-ENN-II can converge with a reliable value of 1.80. In comparison, the FVD value of the PDRS-ENN-III is 1.90. In addition, the forecasting performances of ANFIS, SVM and BPNN are worse than that of PDRS-ENN-I, PDRS-ENN-II and PDRS-ENN-III. Based on Table 11 and Table 12, it can be known:

(1)

The forecasting performances of the proposed models are worse than the fitting performance of the same models. The PDRS-ENN-1, PDRS-ENN-II and PDRS-ENN-1II are better than ANFIS, SVM and BPNN, and the FVD values of PDRS models have changed by 0.17, 0.21 and 0.29, respectively. The FVD values of BPNN have changed by 0.30, which shows the worst stability among the proposed models.

(2)

Though the FVD value of ANFIS have changed by 0.16, showing the best stability among the proposed models, its 3-order-FVD value is only 2.04, which illustrates that the good stability does not generate good forecasting performance in WP, and the PDRS-ENN-I shows the best performance of trade-off between fitting and forecasting among the proposed models in WP.

(3)

All of the proposed forecasting models are data-driven methods, which makes full use of the historical data through feature learning. All of these forecasting models assume that history will repeat itself. The models of ANFIS, SVM and BPNN forecast future values supposing that the independent variables could explain the variations in dependent variables; in addition, these models assume that the relationship between dependent and independent variables will remain valid in the future; however, compared with ANFIS, SVM and BPNN, ENN has a more “context layer” part. Besides, PDRS helps ENN extract the features of WP data, and help ENN avoid the local optimum in training and testing. Therefore, the PDRS models have better performance both in fitting and forecasting.

From Section 5.2.2, we can see that, for WP, the PDRS-ENN is not only suitable for WP fitting but get good results in forecasting as well. In addition, the cross-validation methods are employed in experiments for the reliability and practicability. On the other hand, as a separate and operable method, the first stage of the model, i.e., the PDRS stage, can serve as a candidate correction module after evaluation for other time series forecasting models.

6. Conclusions

A practical machine learning prediction method not only forecasts one single point accurately but is able to accurately forecast the trend that contains several consecutive data points as well. Many algorithms have been developed for STLF and LTLF but these prediction methods are seldom used to deal with complex features of time series. Motivated by recent progress in feature learning-based prediction, we have proposed PDRS-ENN model, which is able to do reasonable prediction in the EL time series. We evaluated and compared PDRS-ENN with both other commonly used forecasting models and traditional models optimized by PDRS, with the load data in NWS, Australia; each sample of them moves steadily upward in secular trend, but is full of noise and hard to simulate. Experimental results showed that the PDRS-ENN generally outperforms traditional models.

We evaluated other variant PDRS-ENNs and found that the PDRS-ENN-I outperforms others in terms of evaluation metrics and degree of certainty. An extension of this work includes keeping the balance of the conflict among different evaluation metrics by handing the forecasting problems with multi-objectives in fitness function. Furthermore, our future research will focus on studying the principles of balancing exploitation and trade-off between fitting and forecasting.