Synchronization of Low-Frequency Oscillation in Power Systems
Abstract
:1. Introduction
2. Sync of Basic Circuits
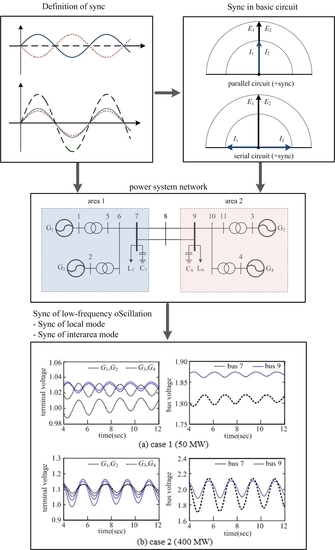
2.1. Definition of Sync
2.2. Sync in Basic Circuits
3. Sync of Low-Frequency Oscillation
3.1. Sync of Local Mode
3.2. Sync of Interarea Mode
3.3. Sync in Wide Area System Operation
4. Numerical Examples
4.1. Two-Area System
4.2. KEPCO System
4.3. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Kundur, P. Power System Stability and Control; McGraw-Hill, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Klein, M.; Rogers, G.; Kundur, P. A fundamental study of inter-area oscillations in power systems. IEEE Trans. Power Syst. 1991, 6, 914–921. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Rogers, G. Power System Oscillations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley & Sons, Ltd.: West Sussex, UK, 2008. [Google Scholar]
- Wang, L.; Semlyen, A. Application of sparse eigenvalue techniques to the small signal analysis of large power systems. IEEE Trans. Power Syst. 1990, 4, 635–642. [Google Scholar] [CrossRef]
- Small Signal Analysis Tool (SSAT). Available online: http://www.dsatools.com/ssat/ (accessed on 25 May 2014).
- Electric Power Research Institute. Small Signal Stability Analysis Program Package ver.3.0; Final Report, TR-101850; EPRI: Palo Alto, CA, USA, 1993. [Google Scholar]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Sync: The Emerging Science of Spontaneous Order; Hyperion Books: New York, NY, USA, 2003. [Google Scholar]
- Earl, M.G.; Strogatz, S.H. Synchronization in oscillator networks with delayed coupling: A stability criterion. Phys. Rev. 2003, 67, 036204. [Google Scholar] [CrossRef] [PubMed]
- Dorfler, F.; Chertkov, M.; Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. USA 2013, 110, 2005–2010. [Google Scholar] [CrossRef] [PubMed]
- Dorfler, F.; Bullo, F. Synchronization and transient stability in power networks and nonuniform Kuramoto oscillators. SIAM J. Control Optim. 2012, 50, 1616–1642. [Google Scholar] [CrossRef]
- Shim, K.S.; Nam, H.K.; Lim, Y.C. Use of Prony analysis to extract sync information of low-frequency oscillation from measured data. Eur. Trans. Electr. Power 2011, 21, 1746–1762. [Google Scholar] [CrossRef]
- Shim, K.S.; Kim, S.T.; Nam, H.K.; Choi, J.H. Initial results of low-frequency oscillation analysis based on PMU in KEPCO system. Trans. Korean Inst. Electr. Eng. 2014, 63, 1–9. [Google Scholar] [CrossRef]
- Cai, G.; Yang, D.; Liu, C. Adaptive wide-Area damping control scheme for smart grids with consideration of signal time delay. Energies 2013, 6, 4841–4858. [Google Scholar] [CrossRef]











| Circuit | Voltage | Load Current | Voltage Phase Difference | |
|---|---|---|---|---|
| Parallel | −sync | –sync | small | 180° |
| +sync | +sync | large | 0° | |
| Serial | –sync | +sync | large | 0° |
| +sync | –sync | small | 180° | |
| Modeno | Mode | Freq (Hz) | Damping (%) | Dominant State | |
|---|---|---|---|---|---|
| Real | Imag | ||||
| 1 | −0.2236 | 3.9364 | 0.6265 | 5.67 | 29252 : GR 4G 22.0 : |
| 2 | −0.5509 | 6.9511 | 1.1063 | 7.90 | 23436 : IC 2ST 16.0 : |
| 3 | −0.5278 | 6.2897 | 1.0010 | 8.36 | 23433 : IC 1ST 16.0 : |
| 4 | −0.5029 | 5.9437 | 0.9460 | 8.43 | 23433 : IC 1ST 16.0 : |
| 5 | −0.5575 | 5.8178 | 0.9259 | 9.54 | 27155 : YG 5G 22.0 : |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shim, K.-S.; Ahn, S.-J.; Choi, J.-H. Synchronization of Low-Frequency Oscillation in Power Systems. Energies 2017, 10, 558. https://doi.org/10.3390/en10040558
Shim K-S, Ahn S-J, Choi J-H. Synchronization of Low-Frequency Oscillation in Power Systems. Energies. 2017; 10(4):558. https://doi.org/10.3390/en10040558
Chicago/Turabian StyleShim, Kwan-Shik, Seon-Ju Ahn, and Joon-Ho Choi. 2017. "Synchronization of Low-Frequency Oscillation in Power Systems" Energies 10, no. 4: 558. https://doi.org/10.3390/en10040558
APA StyleShim, K. -S., Ahn, S. -J., & Choi, J. -H. (2017). Synchronization of Low-Frequency Oscillation in Power Systems. Energies, 10(4), 558. https://doi.org/10.3390/en10040558