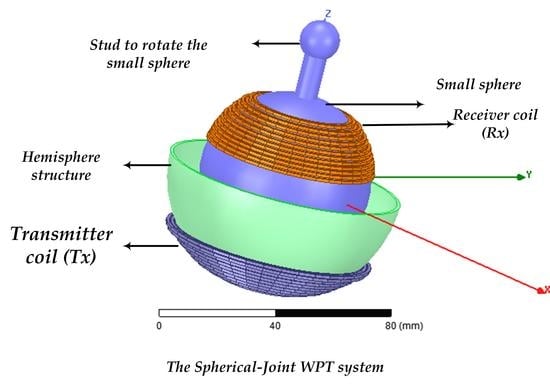
Free Angular-Positioning Wireless Power Transfer Using a Spherical Joint
Abstract
:1. Introduction
2. Optimized Design Method of the Joint WPT System
2.1. Design Method and Algorithm Design
- Enter the radius of the transmitter coil rs = 38.5 mm, the radius of the receiver coil rb = 28.5 mm, and pitch between turns P = 0.5 mm.
- Enter β,. // (radian).
- Size constraints: 0 ≤ zim ≤ rs; the turns can cover the whole space of the hemisphere of the transmitter structure, which means: 0 ≤ ≤ (π/2). On the other hand, 10 ≤ zjn ≤ 2 rb; the turns can occupy the whole space of the sphere, which means: 0 ≤ β ≤ (π). Moreover, zim and zjn are the z-position of the transmitter and receiver turns, respectively.
- Initialize zim, β, and as 0. Initialize zjn = 10 mm (start the z-position for Rx), N1 = 0, N2 = 0, m = 0, and n = 0.
- Count: = + (1/36) π, β = β + (1/36) π, N1 = N1 + 1, N2 = N2 + 1, zim = zim + P, and zjn = zjn + P. In addition, m = m + 1, n = n + 1. // Increment angles to determine the z-position and radius for each turn of the transmitter and receiver windings ((1/36) π is the assumed step). Increment N1, N2 to find the number of turns for both coils. Move the turns in the z-direction with the pitch between coils equal to 0.5 mm. The number of turns can be calculated by N1 = zim/P and N2 = zjm/P.
- Calculate rim = rs sin (), rjn = rb sin (β), zim = rs (1 − cos ()), zjn = rb (1 − cos (β)). //mm (based on angles). rim and rjn are the radii of the transmitter and receiver turns, respectively.
- Calculate L1, L2: the self-inductances of the transmitter coil and receiver coil, respectively. Calculate and maximize the mutual inductance M, calculate the coefficient coupling k, and determine the required capacitors C1, C2. // In order to maximize the mutual inductance, the inductances will be adjusted based on the number of turns and the space between turns (pitch). The transferring distance between Tx and Rx will determine the coupling coefficient, which should be less than a certain value ks.
- With the available value of the frequency and calculated resistances (R1 for Tx and R2 for Rx), calculate the quality factor, transferred power, and efficiency.
- Sweep the frequency and mutual inductance to maximize the efficiency and transferred power.
- Is k < ks, if yes go to 11, or else go to step 13. // The coupling coefficient should stay within a certain range to avoid cases with very low values or cases with very high coupling between Tx and Rx.
- If < π/2 go to step 12, else go to step 13.
- If β < π, go to step 2, else proceed to step 13.
- End.
2.2. Circuit Analysis
3. Simulation Results
4. Magnetic Field Density of the WPT System and Mitigation Methods
4.1. Magnetic Field Density
4.2. Mitigation Methods
4.2.1. Active Shielding
4.2.2. Metallic Shielding
5. Fabrication of the WPT System and Experimental Results
5.1. Measurements and Discussions
5.2. Measurements without Converters
5.3. Comparative Study with Other Research Works
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, C.; Sun, Y.; Wang, Z.; Tang, C. Multi-load mode analysis for electric vehicle wireless supply system. Energies 2018, 11, 1925. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, F.; Hofmann, H.; Liu, W.; Mi, C. A four-plate compact capacitive coupler design and LCL-compensated topology for capacitive power transfer in electric vehicle charging application. IEEE Trans. Power Electron. 2016, 31, 8541–8551. [Google Scholar]
- Yang, Y.; El Baghdadi, M.; Lan, Y.; Benomar, Y.; Van Mierlo, J.; Hegazy, O. Design methodology, modeling, and comparative study of wireless power transfer systems for electric vehicles. Energies 2018, 11, 1716. [Google Scholar] [CrossRef]
- Inoue, K.; Kusaka, K.; Itoh, J.I. Reduction in radiation noise level for inductive power transfer systems using spread spectrum techniques. IEEE Trans. Power Electron. 2018, 33, 3076–3085. [Google Scholar] [CrossRef]
- Tang, S.C.; Lun, T.L.T.; Guo, Z.; Kwok, K.W.; McDannold, N.J. Intermediate range wireless power transfer with segmented coil transmitters for implantable heart pumps. IEEE Trans. Power Electron. 2017, 32, 3844–3857. [Google Scholar] [CrossRef]
- Kang, S.H.; Choi, J.H.; Jung, C.W. Magnetic resonance wireless power transfer using three-coil system with single planar receiver for laptop applications. IEEE Trans. Consum. Electron. 2015, 61, 160–166. [Google Scholar]
- Kan, T.; Mai, R.; Mercier, P.P.; Mi, C.C. Design and analysis of a three-phase wireless charging system for lightweight autonomous underwater vehicles. IEEE Trans. Power Electron. 2017. [Google Scholar] [CrossRef]
- Sugino, M.; Kondo, H.; Takeda, S. Linear motion type transfer robot using the wireless power transfer system. In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24–28 October 2016; pp. 508–509. [Google Scholar]
- Vamvakas, P.; Tsiropoulou, E.E.; Vomvas, M.; Papavassiliou, S. Adaptive power management in wireless powered communication networks: A user-centric approach. In Proceedings of the IEEE 38th Sarnoff Symposium, Newark, NJ, USA, 18–20 September 2017; pp. 1–6. [Google Scholar]
- Bi, S.; Zeng, Y.; Zhang, R. Wireless powered communication networks: An overview. IEEE Wirel. Commun. 2016, 23, 10–18. [Google Scholar] [CrossRef]
- Wu, Q.; Tao, M.; Kwan Ng, D.W.; Chen, W.; Schober, R. Energy-efficient resource allocation for wireless powered communication networks. IEEE Trans. Wirel. Commun. 2016, 15, 2312–2327. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Mitsis, G.; Papavassiliou, S. Interest-aware energy collection & resource management in machine to machine communications. Ad Hoc Netw. 2018, 68, 48–57. [Google Scholar]
- Choi, K.W.; Aziz, A.A.; Setiawan, D.; Tran, N.M.; Ginting, L.; Kim, D.I. Distributed wireless power transfer system for internet of things devices. IEEE Internet Things J. 2018, 5, 2657–2671. [Google Scholar] [CrossRef]
- Khang, S.T.; Lee, D.J.; Hwang, I.J.; Yeo, T.D.; Yu, J.W. Microwave power transfer with optimal number of rectenna arrays for midrange applications. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 155–159. [Google Scholar] [CrossRef]
- De Santi, C.; Meneghini, M.; Caria, A.; Dogmus, E.; Zegaoui, M.; Medjdoub, F.; Kalinic, B.; Cesca, T.; Zanoni, E. GaN-based laser wireless power transfer system. Materials 2018, 11, 153. [Google Scholar] [CrossRef]
- Li, Q.; Deng, Z.; Zhang, K.; Wang, B. Precise attitude control of multirotary-joint solar-power satellite. J. Guid. Control Dyn. 2018, 41, 1435–1442. [Google Scholar] [CrossRef]
- Kim, J.; Kim, D.H.; Choi, J.; Kim, K.H.; Park, Y.J. Free-positioning wireless charging system for small electronic devices using a bowl-shaped transmitting coil. IEEE Trans. Microw. Theory Tech. 2015, 63, 791–800. [Google Scholar] [CrossRef]
- Mei, H.; Thackston, K.A.; Bercich, R.A.; Jefferys, J.G.R.; Irazoqui, P.P. Cavity resonator wireless power transfer system for freely moving animal experiments. IEEE Trans. Biomed. Eng. 2017, 64, 775–785. [Google Scholar] [CrossRef] [PubMed]
- Kuo, R.C.; Riehl, P.; Satyamoorthy, A.; Plumb, W.; Tustin, P.; Lin, J. A 3D resonant wireless charger for a wearable device and a mobile phone. In Proceedings of the 2015 IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 13–15 May 2015. [Google Scholar] [CrossRef]
- Chabalko, M.J.; Sample, A.P. Three-dimensional charging via multimode resonant cavity enabled wireless power transfer. IEEE Trans. Power Electron. 2015, 30, 6163–6173. [Google Scholar] [CrossRef]
- Jeong, I.S.; Jung, B.I.; You, D.S.; Choi, H.S. Analysis of S-parameters in magnetic resonance WPT using superconducting coils. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar] [CrossRef]
- Lin, D.; Zhang, C.; Hui, S.Y.R. Mathematic analysis of omnidirectional wireless power transfer—Part-II three-dimensional systems. IEEE Trans. Power Electron. 2017, 32, 613–624. [Google Scholar] [CrossRef]
- Ye, Z.; Sun, Y.; Liu, X.; Wang, P.; Tang, C.; Tian, H. Power transfer efficiency analysis for omnidirectional wireless power transfer system using three-phase-shifted drive. Energies 2018, 11, 2159. [Google Scholar] [CrossRef]
- Fu, X.; Liu, F.; Chen, X. Optimization of coils for a three-phase magnetically coupled resonant wireless power transfer system oriented by the zero-voltage-switching range. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3708–3713. [Google Scholar]
- Kim, M.; Kim, H.; Kim, D.; Jeong, Y.; Park, H.H.; Ahn, S. A three-phase wireless-power-transfer system for online electric vehicles with reduction of leakage magnetic fields. IEEE Trans. Microw. Theory Tech. 2015, 63, 3806–3813. [Google Scholar] [CrossRef]
- Luo, Z.; Wei, X. Analysis of square and circular planar spiral coils in wireless power transfer system for electric vehicles. IEEE Trans. Ind. Electron. 2018, 65, 331–341. [Google Scholar] [CrossRef]
- Park, C.; Lee, S.; Cho, G.H.; Rim, C.T. Innovative 5-m-off-distance inductive power transfer systems with optimally shaped dipole coils. IEEE Trans. Power Electron. 2015, 30, 817–827. [Google Scholar] [CrossRef]
- Hekal, S.; Abdel-Rahman, A.B.; Jia, H.; Allam, A.; Barakat, A.; Pokharel, R.K. A novel technique for compact size wireless power transfer applications using defected ground structures. IEEE Trans. Microw. Theory Tech. 2017, 65, 591–599. [Google Scholar] [CrossRef]
- Sis, S.A.; Orta, E. A cross-shape coil structure for use in wireless power applications. Energies 2018, 11, 1094. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Z.; Li, J.; Guo, Y.; Xu, B. A Planar L-Shape Transmitter for a Wireless Power Transfer System. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 960–963. [Google Scholar] [CrossRef]
- Abou Houran, M.; Yang, X.; Chen, W. Magnetically coupled resonance WPT: review of compensation topologies, resonator structures with misalignment, and EMI diagnostics. Electronics 2018, 7, 296. [Google Scholar] [CrossRef]
- Liu, D.; Hu, H.; Georgakopoulos, S.V. Misalignment sensitivity of strongly coupled wireless power transfer systems. IEEE Trans. Power Electron. 2016, 32, 5509–5519. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Y.; Jiang, D.; Ruan, X.; Chen, X. Modeling and optimization of magnetically coupled resonant wireless power transfer system with varying spatial scales. IEEE Trans. Power Electron. 2017, 32, 3240–3250. [Google Scholar] [CrossRef]
- Samanta, S.; Rathore, A.K. A New Current-Fed CLC Transmitter and LC receiver topology for inductive wireless power transfer application: analysis, design, and experimental results. IEEE Trans. Transp. Electrif. 2015, 1, 357–368. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, D.; Hui, S.R. Ball-joint wireless power transfer systems. IEEE Trans. Power Electron. 2018, 33, 65–72. [Google Scholar] [CrossRef]
- Tanabe, F.; Yoshimoto, S.; Noda, Y.; Araki, T.; Uemura, T.; Takeuchi, Y.; Imai, M.; Sekitani, T. Flexible sensor sheet for real-time pressure monitoring in artificial knee joint during total knee arthroplasty. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017. [Google Scholar]
- Qiu, Y.; Li, K.M.; Neoh, E.C.; Zhang, H.; Khaw, X.Y.; Fan, X.; Miao, C. Fun-Knee™: A novel smart knee sleeve for Total-Knee-Replacement rehabilitation with gamification. In Proceedings of the IEEE 5th International Conference on Serious Games and Applications for Health (SeGAH), Perth, Australia, 2–4 April 2017. [Google Scholar] [CrossRef]
- Abou Houran, M.; Yang, X.; Chen, W.; Samizadeh, M. Wireless power transfer: critical review of related standards. In Proceedings of the 2018 International Power Electronics Conference (ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1062–1066. [Google Scholar]
- Narayanamoorthi, R.; Juliet, A.V. IoT enabled home cage with three dimensional resonant wireless power and data transfer scheme for freely moving animal. IEEE Sens. J. 2018, 18, 8154–8161. [Google Scholar] [CrossRef]




































| Case | a1 | b1 | c1 | d1 | e | a2 | b2 | c2 | d2 |
|---|---|---|---|---|---|---|---|---|---|
| A | Aa1 | Ab1 | Ac1 | Ad1 | Ae | Aa2 | Ab2 | Ac2 | Ad2 |
| B | Ba1 | Bb1 | Bc1 | Bd1 | Be | Ba2 | Bb2 | Bc2 | Bd2 |
| C | Ca1 | Cb1 | Cc1 | Cd1 | Ce | Ca2 | Cb2 | Cc2 | Cd2 |
| D | Da1 | Db1 | Dc1 | Dd1 | De | Da2 | Db2 | Dc2 | Dd2 |
| E | Ea1 | Eb1 | Ec1 | Ed1 | Ee | Ea2 | Eb2 | Ec2 | Ed2 |
| WPT | f0 | Number of Turns N1/N2 | Inductances L1/L2 µH | Mutual Inductance M µH, at α = 0° | Coupling Coefficient k at α = 0° | C1/C2 nF |
|---|---|---|---|---|---|---|
| Equator windings (single layer) | 500 kHz | 20/17 | 28.971/14.25 | 12.27 | 0.604 | 7.1/3.49 |
| Hemisphere windings (single layer) | 21/16 | 21.14/7.8156 | 7.478 | 0.58177 | 4.793/12.96 | |
| Double-layer windings | 34/22 | 60.71/34.25 | 9.31 | 0.204 | 1.66/3 | |
| Modified Hemisphere windings (multi-layer) | 34/24 | 50.08/29.57 | 17.842 | 0.463 | 2/3.4 | |
| Optimal model | 34/24 | 50.699/29.88 | 3.6117 | 0.089 | 2/3.4 |
| Suppression Methods | N1/N2 and Thickness | Inductances L1/L2 µH | M µH (α = 0°) | k at α = 0° | C1/C2 nF (at 500 kHz) | Efficiency at 50 Ω | Advantages/Disadvantages |
|---|---|---|---|---|---|---|---|
| Optimal model without shield | 34/24 | 50.699/29.88 | 3.6117 | 0.089 | 2/3.4 | 95.26% | Unsafe EMFs in the coil’s vicinities. |
| Active shielding (shielding coils are part of Tx and Rx) | 37/26 (34/24 with shield turns 3/2) | 41.515/25.6 | 2.545 | 0.078 | 2.44/3.95 | 91.15% | Generates magnetic fields, which oppose the one generated by WPT, but causes low PTE. |
| Active shielding (shielding coils are separated from Tx and Rx) | Tx/Rx: 34/24 Shielding coils: three turns with Tx and two with Rx | 50.697/29.87 Shielding coils: 1.428/0.568 | 3.536 | 0.090 | 2/3.4 | 92.18% | Lower leakage MF, but requires many turns and extra layers, which is limited by size and weight. |
| Metallic shielding (only Tx) | Shield: 1 mm | 50.82/29.93 | 3.600 | 0.0923 | 2/3.4 | 93.99% | Suppress EMF around Tx and high leakage MF around Rx. |
| Shield: 2 mm | 50.82/29.93 | 3.610 | 0.0921 | 2/3.4 | 93.97% | ||
| Metallic shielding (Tx and Rx) | Shield: 0.3 mm | 50.81/29.92 | 3.612 | 0.0926 | 2/3.4 | 94.07% | Ensures the safety of the WPT system. |
| WPT System | f0 | Number of Turns N1/N2 | Measured Inductances L1/L2 µH | Measured Resistances R1, R2 Ω | C1/C2 nF |
|---|---|---|---|---|---|
| Double-layer windings | 496 kHz | 32/24 | 60.4/33.12 | 0.22/0.13 | 1.67/3 |
| Optimal model | 27/26 | 52.45/31.7 | 0.18/0.11 | 1.93/3.19 |
| Double-Layer Model: Vin = 10 (RMS) RL = 30 Ω | Optimal Model: Vin = 10 (RMS) RL = 30 Ω | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| α | Input Power Pin W | Output Power Pout W | Measured Efficiency | Simulated Efficiency | α | Input Power Pin W | Output Power Pout W | Measured Efficiency | Simulated Efficiency |
| 0° | 2.73 | 2.31 | 84.60% | 94.3% | 0° | 4.91 | 4.23 | 86.15% | 94.92% |
| 10° | 2.44 | 2.07 | 84.59% | 93.9% | 15° | 5.76 | 4.97 | 86.30% | 94.49% |
| 20° | 2.41 | 2.05 | 84.90% | 95.55% | 30° | 5.10 | 4.42 | 86.55% | 95.14% |
| 30° | 2.27 | 1.94 | 85.42% | 96.06% | 45° | 3.707 | 3.22 | 86.86% | 96.02% |
| 40° | 2.32 | 2.02 | 86.79% | 97.72% | 60° | 3.06 | 2.67 | 87.11% | 96.76% |
| 50° | 2.18 | 1.89 | 86.55% | 95.7% | 75° | 2.90 | 2.53 | 87.27% | 96.85% |
| 60° | 2.03 | 1.70 | 84.61% | 93.89% | 85° | 5.36 | 4.65 | 86.73% | 96.04% |
| 70° | 2.02 | 1.69 | 83.24% | 91.03% | Of note: The measured efficiency is DC-DC, and simulated efficiency is coil-to-coil. | ||||
| 80° | 2.00 | 1.47 | 73.25% | 81.93% | |||||
| 85° | 1.61 | 0.98 | 60.87% | 74.15% | |||||
| Reference/Topology | Size of the 3D Structure (all in cm) | Number of Turns | L1/L2 (µH) | Frequency | Output Power | Efficiency DC-DC |
|---|---|---|---|---|---|---|
| This work/SS | Hemisphere radius: 3.85, small sphere radius: 2.85 | 34/22 | 52.45/31.7 | 496 kHz | 5 W | 86% at 30-Ω load and α = 0°. |
| [17] Series-parallel SP | Tx diameter is 5.8 with thickness of 0.91. Rx volume: 0.105 × 0.65 × 0.246 | 14/16 | - | 6.78 MHz | - | 28% |
| [19] | Tx: 16-gauge wire around plastic coil form, and Rx: spiral coil 0.29 × 0.31. | 16-gauge wire for Tx and 9 turns for Rx. | 1.3/3.55 | 6.78 MHz | Watch: 1 W + Mobile: 5 W | 48% |
| [35] SS | the ball radius: 4 and socket radius: 5 | 41/14 | 70/18.3 | 585 kHz | 4 W | 85.73% at 51 Ω load. |
| [39] | 3D Spiral Tx coil | 3/1 | 2.53/0.025 | Up to 1 MHz | - | 90% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abou Houran, M.; Yang, X.; Chen, W. Free Angular-Positioning Wireless Power Transfer Using a Spherical Joint. Energies 2018, 11, 3488. https://doi.org/10.3390/en11123488
Abou Houran M, Yang X, Chen W. Free Angular-Positioning Wireless Power Transfer Using a Spherical Joint. Energies. 2018; 11(12):3488. https://doi.org/10.3390/en11123488
Chicago/Turabian StyleAbou Houran, Mohamad, Xu Yang, and Wenjie Chen. 2018. "Free Angular-Positioning Wireless Power Transfer Using a Spherical Joint" Energies 11, no. 12: 3488. https://doi.org/10.3390/en11123488
APA StyleAbou Houran, M., Yang, X., & Chen, W. (2018). Free Angular-Positioning Wireless Power Transfer Using a Spherical Joint. Energies, 11(12), 3488. https://doi.org/10.3390/en11123488