An Energy-Efficient Cross-Layer Routing Protocol for Cognitive Radio Networks Using Apprenticeship Deep Reinforcement Learning
Abstract
:1. Introduction
- As far as we know, this is the first work that applies DQfD to the large-scale CRN with a single-agent learning framework. We consider the scenario in which an expert source node already exists, and new data flows are generated from another source node. Simultaneously, a small number of relay nodes change their location, and the network topology has little change compared with the previous network scenario. In this case, DQfD is adopted to learn strategies from the expert source node, which speeds up the learning process and achieves better network performance than that of the expert source node.
- To resolve the inefficiency in power adaptation when utilizing responsibility rating, a novel concept called dynamic adjustment rating is introduced, which regulates transmit power adaptively by comparing single-hop latency with double thresholds. This enables the transmit power to transfer multiple levels at each time step, until rational transmit power is achieved, which accelerates power assignment and improves the system performance.
- To save the system memory and further improve the performance, PM-DQfD is proposed. This makes it possible to periodically erase the inessential self-generated data and outdated expert demonstrations to release replay memory. In addition, it reduces data redundancy and optimizes memory structure, which produces better performance. Simulation results show that the proposed method decreases routing delay and enhances energy efficiency, as well as network stability.
2. System Model
3. Construction of Learning Framework
3.1. Dynamic Adjustment Rating
3.2. Construction of Learning Framework
3.2.1. Environment State
3.2.2. Agent’s Action
3.2.3. Reward Function
4. PM-DQfD-Based Energy-Efficient Joint Design Scheme
4.1. Background of Natural DQfD
4.2. Prioritized Memories Deep Q-Learning from Demonstrations
| Algorithm 1 Prioritized Memories Deep Q-learning from Demonstrations |
| 1: Initialize: |
| 2: Input replay memory , demonstration data set , replay period , |
| demonstration ratio , number of pre-training steps and memory size . |
| 3: Initialize the Q-function and the target Q-function. |
| 4: Pre-training: |
| 5: For steps Do |
| 6: Sample transitions randomly from . |
| 7: Compute the overall loss function. |
| 8: Perform gradient descent to update . |
| 9: End For |
| 10: Self-learning: |
| 11: For episode Do |
| 12: Initialize state . |
| 13: For steps Do |
| 14: Choose action based on policy . |
| 15: Execute action and observe reward , state . |
| 16: Store transition in . |
| 17: Sample transitions randomly from with a fraction |
| of the samples from . |
| 18: Compute the overall loss function. |
| 19: Perform gradient descent to update . |
| 20: Calculate MET according to (18). |
| 21: If |
| 22: For Do |
| 23: If |
| 24: Erase the transition from . |
| 25: End For |
| 26: Every steps reset . |
| 27: End For |
| 28: If |
| 29: Erase transitions with the lowest from . |
| 30: End For |
4.3. PM-DQfD-Based Energy-Efficient Cross-Layer Routing Scheme
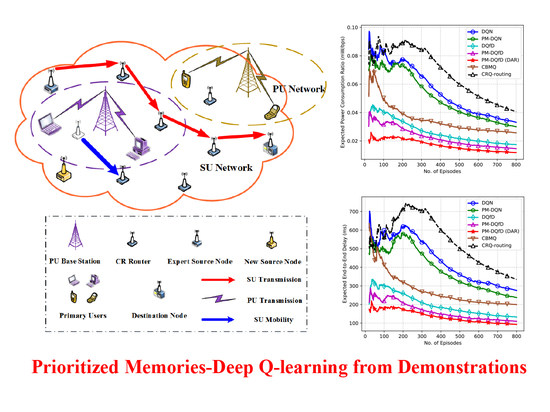
5. Experiment and Evaluation
5.1. Simulation Setup
5.2. Simulation Results
5.3. Time Complexity Analysis
5.4. Discussion of Application Scenario
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ping, S.; Aijaz, A.; Holland, O.; Aghvami, A.H. SACRP: A spectrum aggregation-based cooperative routing protocol for cognitive radio ad-hoc networks. IEEE Trans. Commun. 2015, 63, 2015–2030. [Google Scholar] [CrossRef]
- Hoan, T.N.K.; Koo, I. Multi-slot spectrum sensing schedule and transmitted energy allocation in harvested energy powered cognitive radio networks under secrecy constraints. IEEE Sens. J. 2017, 17, 2231–2240. [Google Scholar] [CrossRef]
- Darsena, D.; Gelli, G.; Verde, F. An opportunistic spectrum access scheme for multicarrier cognitive sensor networks. IEEE Sens. J. 2017, 17, 2596–2606. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, F.; Kumar, S.; Zhu, Y.; Talari, A.; Rahnavard, N.; Matyjas, J.D. A learning-based qoe-driven spectrum handoff scheme for multimedia transmissions over cognitive radio networks. IEEE J. Sel. Areas Commun. 2014, 32, 2134–2148. [Google Scholar] [CrossRef]
- Khan, U.A.; Lee, S.S. Multi-Layer Problems and Solutions in VANETs: A Review. Electronics 2019, 8, 204. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, G.; Liu, W.; Yuan, W.; Cheng, W. Local coordination based routing and spectrum assignment in multi-hop cognitive radio networks. Mob. Netw. Appl. 2008, 13, 67–81. [Google Scholar] [CrossRef]
- Cheng, G.; Liu, W.; Li, Y.; Cheng, W. Joint on-demand routing and spectrum assignment in cognitive radio networks. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 6499–6503. [Google Scholar]
- Wang, J.; Yue, H.; Hai, L.; Fang, Y. Spectrum-aware anypath routing in multi-hop cognitive radio networks. IEEE Trans. Mob. Comput. 2017, 16, 1176–1187. [Google Scholar] [CrossRef]
- Li, D.; Lin, Z.; Stoffers, M.; Gross, J. Spectrum Aware Virtual Coordinates Assignment and Routing in Multihop Cognitive Radio Network. In Proceedings of the 14th IFIP International Conference on Networking, Toulouse, France, 20–22 May 2015. [Google Scholar]
- Zhang, L.; Cai, Z.; Li, P.; Wang, X. Exploiting spectrum availability and quality in routing for multi-hop cognitive radio networks. In Proceedings of the International Conference on Wireless Algorithms, Systems, and Applications, Bozeman, MT, USA, 8–10 August 2016; Springer: Cham, Germany, 2016; pp. 283–294. [Google Scholar]
- Mansoor, N.; Islam, A.M.; Zareei, M.; Baharun, S.; Komaki, S. A novel on-demand routing protocol for cluster-based Cognitive Radio ad-hoc Network. In Proceedings of the TENCON 2016-2016 IEEE Region 10 Conference, Singapore, 22–25 November 2016. [Google Scholar]
- Amini, R.M.; Dziong, Z. An economic framework for routing and channel allocation in cognitive wireless mesh networks. IEEE Trans. Netw. Serv. Manag. 2014, 11, 188–203. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529. [Google Scholar] [CrossRef]
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 1057–1063. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv arXiv:1509.02971, 2015.
- Koushik, A.M.; Hu, F.; Kumar, S. Intelligent spectrum management based on transfer actor-critic learning for rateless transmissions in cognitive radio networks. IEEE Trans. Mob. Comput. 2017, 17, 1204–1215. [Google Scholar]
- Sendra, S.; Rego, A.; Lloret, J.; Jimenez, J.M.; Romero, O. Including artificial intelligence in a routing protocol using software defined networks. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 670–674. [Google Scholar]
- Yu, C.; Lan, J.; Guo, Z.; Hu, Y. DROM: Optimizing the routing in software-defined networks with deep reinforcement learning. IEEE Access 2018, 6, 64533–64539. [Google Scholar] [CrossRef]
- Mustapha, I.; Ali, B.; Rasid, M.; Sali, A.; Mohamad, H. An energy-efficient spectrum-aware reinforcement learning-based clustering algorithm for cognitive radio sensor networks. Sensors 2015, 15, 19783–19818. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Zhang, F.; Xue, L. A Kind of Joint Routing and Resource Allocation Scheme Based on Prioritized Memories-Deep Q Network for Cognitive Radio Ad Hoc Networks. Sensors 2018, 18, 2119. [Google Scholar] [CrossRef] [PubMed]
- Karmokar, A.; Naeem, M.; Anpalagan, A.; Jaseemuddin, M. Energy-efficient power allocation using probabilistic interference model for OFDM-based green cognitive radio networks. Energies 2014, 7, 2535–2557. [Google Scholar] [CrossRef]
- Singh, K.; Moh, S. An energy-efficient and robust multipath routing protocol for cognitive radio ad hoc networks. Sensors 2017, 17, 2027. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Chen, C.; Ma, P.; Xue, L. A Cross-Layer Routing Protocol Based on Quasi-Cooperative Multi-Agent Learning for Multi-Hop Cognitive Radio Networks. Sensors 2019, 19, 151. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Wang, W.; Kwasinski, A.; Niyato, D.; Han, Z. A survey on applications of model-free strategy learning in cognitive wireless networks. IEEE Commun. Surv. Tutor. 2016, 18, 1717–1757. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, F.; Kumar, S.; Matyjas, J.D.; Sun, Q.; Zhu, Y. Apprenticeship learning based spectrum decision in multi-channel wireless mesh networks with multi-beam antennas. IEEE Trans. Mob. Comput. 2017, 16, 314–325. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, F.; Zhu, Y.; Kumar, S. Optimal spectrum handoff control for CRN based on hybrid priority queuing and multi-teacher apprentice learning. IEEE Trans. Veh. Technol. 2017, 66, 2630–2642. [Google Scholar] [CrossRef]
- Hester, T.; Vecerik, M.; Pietquin, O.; Lanctot, M.; Schaul, T.; Piot, B.; Dulac-Arnold, G. Deep Q-learning from demonstrations. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 3223–3231. [Google Scholar]
- Hester, T.; Vecerik, M.; Pietquin, O.; Lanctot, M.; Schaul, T.; Piot, B.; Sendonaris, A.; Dulac-Arnold, G.; Osband, I.; Agapiou, J.; et al. Learning from demonstrations for real world reinforcement learning. arXiv 2017, arXiv:1704.03732. [Google Scholar]
- Andre, D.; Friedman, N.; Parr, R. Generalized prioritized sweeping. In Advances in Neural Information Processing Systems; University of California: Berkeley, CA, USA, 1998; pp. 1001–1007. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. Computer Science. arXiv arXiv:1312.5602v1, 2013.
- Pourpeighambar, B.; Dehghan, M.; Sabaei, M. Non-cooperative reinforcement learning based routing in cognitive radio networks. Comput. Commun. 2017, 106, 11–23. [Google Scholar] [CrossRef]
- Al-Rawi, H.A.; Yau, K.L.A.; Mohamad, H.; Ramli, N.; Hashim, W. A reinforcement learning-based routing scheme for cognitive radio ad hoc networks. In Proceedings of the 2014 7th IFIP Wireless and Mobile Networking Conference (WMNC), Vilamoura, Portugal, 20–22 May 2014; pp. 1–8. [Google Scholar]
- Chen, X.; Zhao, Z.; Zhang, H. Stochastic Power Adaptation with Multiagent Reinforcement Learning for Cognitive Wireless Mesh Networks. IEEE Trans. Mob. Comput. 2013, 12, 2155–2166. [Google Scholar] [CrossRef]












| Parameter | Default Value |
|---|---|
| Link Gain | [34] |
| Available Spectrum | |
| Bandwidth, | |
| AWGN power, | |
| PU-to-SU interference, | |
| Packet Size, | |
| Mean OFF Period of PU, | |
| SINR threshold, | |
| Higher Latency Threshold, | |
| Lower Latency Threshold, | |
| Weighting of the power consumption ratio, | |
| Weighting of the single-hop delay, | |
| Demonstration ratio, | |
| Discount factor, | |
| Learning rate, | |
| Weighting of the supervised loss, | |
| Weighting of L2 regularization loss, | |
| Pre-training step, | |
| Replay period, | |
| Size of Mini-Batch, | |
| Upper Limit of Erasing, | |
| Lower Limit of Erasing, | |
| Erasing Parameter, | |
| Final Size of Demo Buffer, | |
| Erasing parameter of Demo Buffer, | |
| Replay buffer size, | |
| Demonstration buffer size, |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Xu, Y.; Xue, L.; Wang, L.; Zhang, F. An Energy-Efficient Cross-Layer Routing Protocol for Cognitive Radio Networks Using Apprenticeship Deep Reinforcement Learning. Energies 2019, 12, 2829. https://doi.org/10.3390/en12142829
Du Y, Xu Y, Xue L, Wang L, Zhang F. An Energy-Efficient Cross-Layer Routing Protocol for Cognitive Radio Networks Using Apprenticeship Deep Reinforcement Learning. Energies. 2019; 12(14):2829. https://doi.org/10.3390/en12142829
Chicago/Turabian StyleDu, Yihang, Ying Xu, Lei Xue, Lijia Wang, and Fan Zhang. 2019. "An Energy-Efficient Cross-Layer Routing Protocol for Cognitive Radio Networks Using Apprenticeship Deep Reinforcement Learning" Energies 12, no. 14: 2829. https://doi.org/10.3390/en12142829
APA StyleDu, Y., Xu, Y., Xue, L., Wang, L., & Zhang, F. (2019). An Energy-Efficient Cross-Layer Routing Protocol for Cognitive Radio Networks Using Apprenticeship Deep Reinforcement Learning. Energies, 12(14), 2829. https://doi.org/10.3390/en12142829