A Control Scheme without Sensors at the PV Source for Cost and Size Reduction in Two-Stage Grid Connected Inverters
Abstract
:1. Introduction
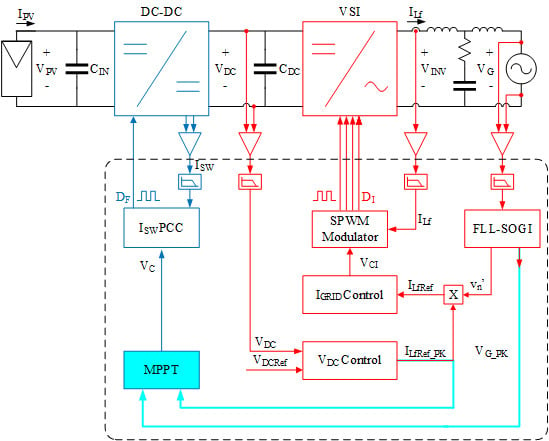
2. Two-Stage Grid-Connected PV Inverter
2.1. Grid-tied VSI
2.2. Step Up DC-DC Converter
3. Control
3.1. Control Scheme of the VSI Stage
3.1.1. Synchronization with the Grid
3.1.2. Control of the Current Injected into the Grid
3.1.3. Control of the DC-link Voltage (VDC)
3.2. Control Scheme of the DC-DC Stage
3.2.1. Peak Current Control of DC-DC Stage
3.2.2. PV Panel Voltage (VPV) Control Loop in the Conventional MPPT
4. MPPT Implementation without VPV and IPV Sensors
4.1. Estimation of the Power Injected into the Grid in the Sensorless MPPT
4.2. Implementation of the Perturb and Observe (P&O) Algorithm
5. Results
5.1. Control of the VSI
5.1.1. Transients of the DC-link Voltage
5.1.2. Influence of the SOGI Notch in the Distortion of the Current Injected to the Grid
5.1.3. Loop Gain Measurement
5.2. MPPT
5.2.1. Start-up Time to Reach the MPP
5.2.2. MPPT Performance Close to the MPP
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Implementation | Conventional | Sensorless and Reduced DC-link | |
|---|---|---|---|
| PCB | 100 € | 100 € | 100 € |
| Common components | 400 € | 400 € | 400 € |
| DC-link | Electrolytic 500 μF 12 € | Electrolytic 50 μF 5 € | Film 50 μF 7 € |
| VPV and IPV sensors | 25 € | 0 € | 0 € |
| Total | 537 € | 505 € (94%) | 507 € (94.4%) |
References
- International Electrotechnical Commission. Electromagnetic Compatibility (EMC)—Part 3-2: Limits—Limits for Harmonic Current Emissions (Equipment Input Current ≤16 A Per Phase); International Electrotechnical Commission (IEC): Geneva, Switzerland, 2018. [Google Scholar]
- International Electrotechnical Commission. Electromagnetic Compatibility (EMC)—Part 3-4: Limits—Limitation of Emission of Harmonic Currents in Low-Voltage Power Supply Systems for Equipment with Rated Current Greater than 16 A; International Electrotechnical Commission (IEC): Geneva, Switzerland, 1998. [Google Scholar]
- International Electrotechnical Commission. Electromagnetic compatibility (EMC)—Part 3-12: Limits—Limits for Harmonic Currents Produced by Equipment Connected to Public Low-Voltage Systems with Input Current >16 A and ≤75 A Per Phase; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2011. [Google Scholar]
- Langella, R.; Testa, A.; Alii, E. IEEE Std 519-2014—IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE Trans. Ind. Appl. 1989, 25, 6–7. [Google Scholar]
- Espi, J.M.; Castello, J. A Novel Fast MPPT Strategy for High Efficiency PV Battery Chargers. Energies 2019, 12, 1152. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Modified P&O Maximum Power Point Tracking Method With Reduced Steady-State Oscillation and Improved Tracking Efficiency. IEEE Trans. Sustain. Energy 2016, 7, 1506–1515. [Google Scholar]
- Sher, H.A.; Rizvi, A.A.; Addoweesh, K.E.; Al-Haddad, K. A Single-Stage Stand-Alone Photovoltaic Energy System With High Tracking Efficiency. IEEE Trans. Sustain. Energy 2017, 8, 755–762. [Google Scholar] [CrossRef]
- Liivik, E.; Chub, A.; Kosenko, R.; Vinnikov, D. Low-cost photovoltaic microinverter with ultra-wide MPPT voltage range. In Proceedings of the 2017 6th International Conference on Clean Electrical Power (ICCEP), Santa Margherita Ligure, Italy, 27–29 June 2017; pp. 46–52. [Google Scholar] [CrossRef]
- Sher, H.A.; Addoweesh, K.E.; Haddad, K.A. An Efficient and Cost-Effective Hybrid MPPT Method for a Photovoltaic Flyback Micro-Inverter. IEEE Trans. Sustain. Energy 2017, 9, 1137–1144. [Google Scholar] [CrossRef]
- Samrat, P.S.; Edwin, F.F.; Xiao, W. Review of current sensorless maximum power point tracking technologies for photovoltaic power systems. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013; pp. 20–23. [Google Scholar] [CrossRef]
- Kitano, T.; Matsui, M.; Xu, D.-H. Power sensor-less MPPT control scheme utilizing power balance at DC link-system design to ensure stability and response. In Proceedings of the IECON 01—27th Annual Conference of the IEEE Industrial Electronics Society, Denver, CO, USA, 29 November–2 December 2001; Volume 2, pp. 1309–1314. [Google Scholar]
- Choi, B.-Y.; Jang, J.-W.; Kim, Y.-H.; Ji, Y.-H.; Jung, Y.-C.; Won, C.-Y. Current sensorless MPPT using photovoltaic AC module-type flyback inverter. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics (ISIE), Taipei, Taiwan, 28–31 May 2013; pp. 28–31. [Google Scholar] [CrossRef]
- Metry, M.; Shadmand, M.B.; Balog, R.S.; Abu-Rub, H. MPPT of Photovoltaic Systems Using Sensorless Current-Based Model Predictive Control. IEEE Trans. Ind. Appl. 2017, 53, 1157–1167. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. A Technique for Improving P&O MPPT Performances of Double-Stage Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Electron. 2009, 56, 4473–4482. [Google Scholar] [CrossRef]
- Garcerá, G.; González-Medina, R.; Figueres, E.; Sandia, J. Dynamic modeling of DC–DC converters with peak current control in double-stage photovoltaic grid-connected inverters. Int.J. Circuit Theory Appl. 2012, 40, 793–813. [Google Scholar] [CrossRef]
- Zhu, G.; Ruan, X.; Zhang, L.; Wang, X. On the Reduction of Second Harmonic Current and Improvement of Dynamic Response for Two-Stage Single-Phase Inverter. IEEE Trans. Power Electron. 2015, 30, 1028–1041. [Google Scholar] [CrossRef]
- Karanayil, B.; Agelidis, V.G.; Pou, J. Performance Evaluation of Three-Phase Grid-Connected Photovoltaic Inverters Using Electrolytic or Polypropylene Film Capacitors. IEEE Trans. Sustain. Energy 2014, 5, 1297–1306. [Google Scholar] [CrossRef]
- Schonberger, J. A single phase multi-string PV inverter with minimal bus capacitance. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar] [CrossRef]
- Messo, T.; Jokipii, J.; Suntio, T. Minimum DC-link capacitance requirement of a two-stage photovoltaic inverter. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 999–1006. [Google Scholar] [CrossRef]
- Heo, J.; Matsuo, K.; Hen, P.; Kondo, K. Dynamics of a minimum DC link voltage driving method to reduce system loss for hybrid electric vehicles. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–7. [Google Scholar]
- Karanayil, B.; Agelidis, V.G.; Pou, J. Evaluation of DC-link decoupling using electrolytic or polypropylene film capacitors in three-phase grid-connected photovoltaic inverters. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 6980–6986. [Google Scholar] [CrossRef]
- Bazargan, D.; Bahrani, B.; Filizadeh, S. Reduced Capacitance Battery Storage DC-link Voltage Regulation and Dynamic Improvement Using a Feedforward Control Strategy. IEEE Trans. Energy Convers. 2018, 33, 1659–1668. [Google Scholar] [CrossRef]
- Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. A New Single-Phase PLL Structure Based on Second Order Generalized Integrator. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Advanced Grid Synchronization System for Power Converters under Unbalanced and Distorted Operating Conditions. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 5173–5178. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Candela, I.; Teodorescu, R.; Blaabjerg, F. Grid synchronization of power converters using multiple second order generalized integrators. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 755–760. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Etxeberria, I.; Hermoso, J.R.; Teodorescu, R. Multiple second order generalized integrators for harmonic synchronization of power converters. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, 2009 ECCE, San Jose, CA, USA, 20–24 September 2009; pp. 2239–2246. [Google Scholar] [CrossRef]
- Rodríguez, P.; Luna, A.; Candela, I.; Mujal, R.; Teodorescu, R.; Blaabjerg, F. Multiresonant Frequency-Locked Loop for Grid Synchronization of Power Converters Under Distorted Grid Conditions. IEEE Trans. Ind. Electron. 2011, 58, 127–138. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. IEEE Trans. Ind. Electron. 2009, 56, 4492–4501. [Google Scholar] [CrossRef]
- TMS320F28335 Delfino™ 32-bit MCU with 150 MIPS, FPU, 512 KB Flash, EMIF, 12b ADC. Available online: http://www.ti.com/product/TMS320F28335 (accessed on 1 May 2019).
- Castilla, M.; Miret, J.; Matas, J.; Garcia de Vicuna, L.; Guerrero, J.M. Control Design Guidelines for Single-Phase Grid-Connected Photovoltaic Inverters With Damped Resonant Harmonic Compensators. IEEE Trans. Ind. Electron. 2009, 56, 4492–4501. [Google Scholar] [CrossRef]
- Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Control of single-stage single-phase PV inverter. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005; pp. 20–26. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Borup, U.; Liserre, M. A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 22–26 February 2004; Volume 1, pp. 580–586. [Google Scholar] [CrossRef]
- Reza, M.S.; Ciobotaru, M.; Agelidis, V.G. Grid voltage offset and harmonics rejection using second order generalized integrator and kalman filter technique. In Proceedings of the 2012 7th International Power Electronics and Motion Control Conference (IPEMC), Harbin, China, 2–5 June 2012; pp. 104–111. [Google Scholar] [CrossRef]
- Timbus, A.V.; Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Adaptive resonant controller for grid-connected converters in distributed power generation systems. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Chapter 9: Grid Converter Control for WTS. In Grid Converters for Photovoltaic and Wind Power Systems; Wiley-IEEE Press: Chichester, England, 2010; pp. 205–235. ISBN 978-0-470-05751-3. [Google Scholar]
- Hohm, D.P.; Ropp, M.E. Comparative study of maximum power point tracking algorithms. Prog. Photovolt. Res. Appl. 2003, 11, 47–62. [Google Scholar] [CrossRef]
- International Standard IEC 61000-4-7. Electromagnetic Compatibility (EMC)—Part 4-7:Testing and Measurement Techniques—General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2002. [Google Scholar]
- Middlebrook, R.D. Measurement of Loop Gain in Feedback Systems. Int. J. Electron. 1975, 38, 485–512. [Google Scholar] [CrossRef]
- Gonzalez-Espin, F.; Figueres, E.; Garcera, G.; Gonzalez-Medina, R.; Pascual, M. Measurement of the Loop Gain Frequency Response of Digitally Controlled Power Converters. IEEE Trans. Ind. Electron. 2010, 57, 2785–2796. [Google Scholar] [CrossRef]
- Gonzalez-Espin, F.; Figueres, E.; Garcera, G.; Gonzalez, R.; Carranza, O.; Gonzalez, L.G. A digital technique to measure the loop gain of power converters. In Proceedings of the 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]



















| Item | Value |
|---|---|
| Topology | Single phase, full-bridge |
| RMS Grid Voltage: VG | 230 VAC |
| Grid frequency: FG | 50 Hz |
| Rated Output Power: PG | 230 W |
| Max Current: IG | 1 A |
| Modulation | Unipolar SPWM |
| Inverter switching Frequency: FSW_I | 20 kHz |
| Sampling Frequency: FS | 40 kHz |
| Filter Inductance: Lf | 38 mH |
| Filter Capacitance: Cf | 330 nF |
| Damping Resistor: Rf | 50 Ω |
| Grid Inductance estimation: Lg | 1.5 mH (strong grid) 3 mH (standard grid) 6 mH (weak grid) |
| DC-link Voltage: VDC | 380 V |
| DC-link Voltage Ripple: VDC_R | 10% of VDC (38 Vpk-pk) |
| DC-link Capacitance: CDC | 50 µF |
| Item | Value |
|---|---|
| Topology | Flyback |
| DC Input Voltage: VPV | 24 V to 35 V at the MPPT |
| DC Output Voltage: VDC | 380 V |
| Rated Input Power: PPV | 230 W |
| Max Input Current: IPV | 8 A |
| Flyback converter switching Frequency: FSW_F | 24 kHz |
| Input Capacitance: CIN | 4 mF |
| Transformer Turns Ratio: N = N1/N2 | 1/16 |
| Transformer Magnetizing Inductance: LM | 10 µH |
| Conduction Mode | Discontinuous (DCM) |
| Constant | Value |
|---|---|
| KPLf | 0.65 |
| KRLf1 | 100 |
| KBWRLf1 | 0.02 |
| KRLf3 | 100 |
| KBWRLf3 | 0.02/3 |
| KRLf5 | 100 |
| KBWRLf5 | 0.02/5 |
| KRLf7 | 25 |
| KBWRLf7 | 0.02/7 |
| MPPT Implementation | Conventional | Sensorless |
|---|---|---|
| Average power (W) | 225.30 | 224.80 |
| Peak power (W) | 225.49 | 225.11 |
| Tracking efficiency (%) | 99.92 | 99.86 |
| Stage | Irradiation Profile | Duration |
|---|---|---|
| 1 | Constant at 1000 W/m2 | 10 s |
| 2 | Linear decrease from 1000 W/m2 to 600 W/m2 | 10 s |
| 3 | Constant at 600 W/m2 | 10 s |
| 4 | Linear increase from 600 W/m2 to 1000 W/m2 | 10 s |
| 5 | Constant at 1000 W/m2 | 10 s |
| Total | - | 50 s |
| Stage | Conventional MPPT | Sensorless MPPT | % |
|---|---|---|---|
| 1 | 225.30 W | 224.80 W | 0.998 |
| 2 | 181.27 W | 173.51 W | 0.957 |
| 3 | 134.90 W | 134.41 W | 0.996 |
| 4 | 180.82 W | 180.36 W | 0.997 |
| 5 | 225.30 W | 224.80 W | 0.998 |
| Average | 189.52 W | 187.58 W | 0.989 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Medina, R.; Liberos, M.; Marzal, S.; Figueres, E.; Garcerá, G. A Control Scheme without Sensors at the PV Source for Cost and Size Reduction in Two-Stage Grid Connected Inverters. Energies 2019, 12, 2955. https://doi.org/10.3390/en12152955
González-Medina R, Liberos M, Marzal S, Figueres E, Garcerá G. A Control Scheme without Sensors at the PV Source for Cost and Size Reduction in Two-Stage Grid Connected Inverters. Energies. 2019; 12(15):2955. https://doi.org/10.3390/en12152955
Chicago/Turabian StyleGonzález-Medina, Raúl, Marian Liberos, Silvia Marzal, Emilio Figueres, and Gabriel Garcerá. 2019. "A Control Scheme without Sensors at the PV Source for Cost and Size Reduction in Two-Stage Grid Connected Inverters" Energies 12, no. 15: 2955. https://doi.org/10.3390/en12152955
APA StyleGonzález-Medina, R., Liberos, M., Marzal, S., Figueres, E., & Garcerá, G. (2019). A Control Scheme without Sensors at the PV Source for Cost and Size Reduction in Two-Stage Grid Connected Inverters. Energies, 12(15), 2955. https://doi.org/10.3390/en12152955