Reaction Kinetics and Coreflooding Study of High-Temperature Carbonate Reservoir Stimulation Using GLDA in Seawater

Abstract

Well stimulation using hydrochloric acid (HCl) is a common practice in carbonate reservoirs to overcome formation damage in the near wellbore area. Using HCl for matrix acidizing has many limitations at high-temperature (HT) conditions, such as tubulars corrosion and face dissolution due to the fast reaction rate. Chelating agents, such as L-glutamic acid-N,N-diacetic acid (GLDA), are alternatives to HCl to overcome these problems. We studied the effect of diluting GLDA in seawater on the reaction kinetics with carbonate rocks under HT conditions at low pH (3.8). Results of the reaction of carbonate at 1000 psi and 150, 200, and 250 °F with GLDA prepared in both fresh and seawater, GLDA/DI and GLDA/SW, respectively, are presented. The reaction kinetics experiments were carried out in HT rotating disk apparatus (RDA) at rotational speeds ranging from 500 to 2000 revolutions per minute (RPM) at a fixed temperature. Indiana limestone and Austin chalk were used to studying the effect of rock facies on the reaction of GLDA with rock samples. In both GLDA/DI and GLDA/SW, the reaction regime of 20 wt% GLDA (3.8 pH) with Indiana limestone was mass transfer limited. The reaction rate and diffusion coefficient were highly dependent on the temperature. For Austin chalk, at 200 °F and 1000 psi the diffusion coefficient of GLDA/SW is an order of magnitude of its value with Indiana limestone using the same fluid. Diffusion coefficients were used to estimate the optimum injection rate for stimulating HT carbonate formation and compared with coreflooding results. The data presented in this paper will support the numerical simulation of the acid flow in carbonate reservoirs.

1. Introduction

Organic and inorganic acids are often injected into carbonate reservoirs to improve oil and gas production. These acids are usually selected based on the type of reservoir rock. In the case of stimulating carbonate formations, acids can dissolve the carbonate rock matrix and create different dissolution features or structures depending on the acid type, injection rate, and formation conditions [1,2,3,4,5,6]. Face-dissolution usually results from very low injection rates which give more time for dissolution of the rock face a pattern [7]. When the retention time of acid in the rock is small, narrow dissolution channels are formed and propagate through the rock and form more branches with continuous acid injection [8,9]. An optimum channel formed during acid injection at the minimum volume of acid injected and yield the highest permeability increase is known as a wormhole [4,10,11]. Other dissolution patterns may present, such as conical wormholes, at an injection rate between face dissolution and the optimum wormhole, and ramified wormholes at an injection rate between the optimum wormhole and uniform dissolution patterns.

The acid type affects the structure of wormholes generated during carbonate acidizing [7,12]. Slow reacting acids, such as chelating agents and other organic acids form wider, less branched wormholes, while highly reactive acids, such as HCl, form highly branched wormholes [13]. The relative magnitudes of acid transport and reaction rates define the controlling step of the dissolution reaction whether kinetically controlled or mass-transfer controlled [14]. As a result, the wormhole structure depends on the acid diffusivity and reactivity, in addition to the acid-injection rate [15]. To characterize acid transport to rock surface during matrix acidizing, the acid diffusion coefficient is an important parameter to be determined under reservoir conditions [16].

2. Chelating Agents

Chelating agents can sequester metal ions through coordination bonds and prevent any further interaction with other ions present in the solution. The chelating agent type and the metal ion properties highly affect the stability of the formed organic [17].

The low corrosiveness nature of chelating agents enables using it in different aspects of the oil and gas industry including scale removal from electrical submersible pumps in oil production wells [18], Scale inhibition [19,20], Filter cake removal after drilling operations [21]. In addition, aminocarboxylic acids were used to improve oil recovery from subsurface hydrocarbon reservoirs [22,23]. Different chelating agents were also used as standalone stimulation fluids at a wide range of pH values at high-pressure high-temperature (HPHT) conditions [24,25].

GLDA is an aminopolycarboxylic acid (Figure 1), which can form stable complexes with different alkali earth metals (Ca, Fe, Mg, etc.) with a low corrosiveness to the equipment up to 300 °F [26]. It is produced from a bio-based naturally-occurring amino acid known as monosodium L-glutamic acid. GLDA is favorable because of its improved biodegradability properties, such as being readily biodegradable with high solubility in fresh water over a wide pH range [27]. Studies were done before proved the effectiveness of using GLDA for well stimulation in both sandstone and carbonate reservoirs [26,28,29]. Limitation of using EDTA in seawater base is chemical precipitation at low pH values while GLDA can be prepared in sweater at high concentrations (up to 20 wt%) without any precipitation problems [30]. For these reasons, GLDA was selected as the stimulation fluid in this study because of its high stability at higher concentration commonly used for matrix acidizing and lower pH when prepared in seawater.

GLDA undergoes stepwise deprotonation to reach a fully ionized state. The calcite dissolution rate by the GLDA chelating agent depends on the GLDA pH. The form of the ionic species of GLDA is dictated by a dissociation reactions series. For GLDA (a chelating agent with four carboxylic acid groups), the acid dissociation constants (pKa) values at an ionic strength of 0.1 M and 25 °C are shown in

Table 1. The acid dissociation constants (pKa) for 0.1 M GLDA at 25 °C [31].

Dissociation	pKa
${\mathrm{H}}_4\mathrm{Y}\rightleftharpoons {\mathrm{H}}_3{\mathrm{Y}}^{-1}+{\mathrm{H}}^{+}$	pKa1 = 9.4
${\mathrm{H}}_3{\mathrm{Y}}^{-1}\rightleftharpoons {\mathrm{H}}_2{\mathrm{Y}}^{-2}+{\mathrm{H}}^{+}$	pKa2 = 5.0
${\mathrm{H}}_2{\mathrm{Y}}^{-2}\rightleftharpoons {\mathrm{HY}}^{-3}+{\mathrm{H}}^{+}$	pKa3 = 3.5
${\mathrm{HY}}^{-3}\rightleftharpoons {\mathrm{Y}}^{-4}+{\mathrm{H}}^{+}$	pKa4 = 2.6

in which H_mY^m–n is the chelating agent molecule, m is the number of acidic protons, and n is number of carboxylic acid groups, i.e., 4. Reaction of high GLDA pH solutions (Y⁻⁴) are primarily driven by the chelation process, which generally has a much lower reaction rate than the acid dissolution process and gives 1:1 ratio between the chelate and calcium ions. In the intermediate pH range, both processes will contribute to the overall dissolution rate. As pH increases from 1.7 to 13, the GLDA successively deprotonated from H₄Y to Y⁻⁴ thereby losing the ability to donate H⁺ ions as pH increased. The reaction rate of GLDA at high pH values is dominated by chelation and is expected to be significantly slower than that at low pH values.

GLDA showed promising results when used to stimulate HPHT carbonate and sandstone reservoirs in many laboratory studies [26,27,32] as well as field treatments [33,34]. GLDA is being used as an alternative to HCl in order to overcome the challenges of HPHT environments such as well tubulars corrosion, face dissolution due to uncontrolled high reaction rate, and formation damage due to sludge formation. In addition, GLDA also acts as an iron control agent and it is less corrosive to the well tubulars. HCl needs numerous additives, which will increase the cost of the matrix acidizing. HCl based matrix acidizing formulations are usually loaded with additives, such as corrosion inhibitors, water-wetting surfactants, iron control agent, anti-sludge agents, iron control agents, etc. GLDA acid treatment does not require any additives since GLDA itself acts as iron control agent, has low interfacial tension (IFT), acts as surfactant, and does not cause asphaltene precipitation [35]. Using GLDA will eliminate the need for the numerous additives used in the case of HCl treatment.

Performing the reaction kinetics experiments of stimulation fluids using RDA will enable the optimization of tedious and expensive coreflooding experiments and will facilitate the stimulation design for any damage radius. To locate the optimum injection rate for each damage penetration, several corefloods are needed. For example, the optimum injection rate and hence the optimum Damköhler number can be determined using the diffusion coefficient of the mass transfer limited reactions. The diffusion coefficient is obtained from a series of reaction kinetics experiments using the RDA.

To the authors’ knowledge, this is the first time to report the reaction kinetics of GLDA chelating agent prepared in seawater with calcite rock samples using RDA at HPHT. The reaction regimes and the diffusion coefficients of GLDA are determined. In addition, we investigate the effect of porosity type (rock facie) on the rock fluid interaction by comparing the reaction of two different carbonate rocks having similar mineralogy but different porosity type with the same fluid system.

3. Rotating Disk Theory

During a matrix acidizing treatment, an acidic fluid is injected into the reservoir rock, the reaction regime is greatly affected by both reactant and products transport to and from the rock surface [14]. The three steps making the overall reaction are (Figure 2):

-

Reactant transport to the rock surface.

-

Reaction at the rock surface.

-

Products transport from the rock surface.

The slowest step is known as “the rate-limiting step” since it will control the overall reaction kinetics. For example, if the surface reaction rate is slower than the mass transfer process, then the reaction is surface reaction limited [36]. On the other hand, if the reactants and products diffusion to/from the surface is slower than the surface reaction rate, the process is mass transfer limited.

In the case of Newtonian fluids, the mass transfer rate ($R_{MT})$ of a reactant to the solid surface in a laminar flow regime induced by a rotating disk geometry is given by the following Equation [37,38]:

$$J_{mt}=k_m\left(C_b-C_s\right)$$

(1)

$$k_m=\frac{0.60248\left({S_c}^{-\frac{2}{3}}\right)\sqrt{\nu \omega }}{1+0.2980\left({S_c}^{-\frac{1}{3}}\right)+0.1451\left({S_c}^{-\frac{2}{3}}\right)}$$

(2)

where J_mt is the mass transfer flux, C_b is the transferred species bulk concentration, C_s is the transferred species surface concentration, k_m is the mass transfer coefficient, $\omega$ is disk angular velocity (equal to 2πN, N is the number of cycles/s or rad/s), $\rho$ is the density of the bulk fluid (gm/cm³), µ is the viscosity of the bulk fluid (gm/s.cm), ν is the kinematic viscosity (cm²/s), S_c is Schmidt number (ν/D_e), dimensionless, and D_e is the diffusion coefficient (cm²/s).

For reactions limited by mass transfer, C_s can be neglected (C_s ≈ 0). Then Equation (1) can be written as:

$$J_{mt}=\frac{0.60248{\left(\frac{\mu }{\rho D_e}\right)}^{-\frac{2}{3}}{\mathrm{C}}_b\sqrt{\frac{\mu }{\rho }}}{1+0.2980{\left(\frac{\mu }{\rho D_e}\right)}^{-\frac{1}{3}}+0.1451{\left(\frac{\mu }{\rho D_e}\right)}^{-\frac{2}{3}}}{\omega }^{\frac{1}{2}}$$

(3)

For laminar flow regime around a rotating disk, Reynold’s number is in the order of 10⁴–10⁵ and is defined as [37]:

$$N_{Re}=\frac{\omega R^2}{\nu }$$

(4)

where R is the radius of the rotating disk (cm). For the RDA reactor’s geometry, the laminar flow occurs when Reynold number is below 3 × 10⁵ compared to 2000 in pipe flow [39,40]. In this work Equation (3) was used to interpret the results as N_Re is less than 10⁴ (highest N_Re is 804 at 2000 RPM). In addition, the fluids used (20 wt% GLDA/DI and 20 wt% GLDA/SW) are Newtonian fluids [31]. The surface reaction rate can be described as a function of concentration by the following Equation [41]:

$$-r_{HCl}=k{C}_{As}^n=J_{mt}$$

(5)

where $r_{HCl}$ is the dissolution rate per unit area (moles/cm²∙s), k is the Specific reaction rate (moles/cm²∙s)(mole/cm³)^–n, C_As is the concentrations of the dissolving substance (A) at the reaction surface (moles/cm³), and n is reaction order which is dimensionless. GLDA in the acidic form will react mainly by hydrogen attack in addition to chelation. This equation describes the reaction of adsorbed H⁺ with the solid surface. The dissolution rate is the slope of the straight line between calcium concentration and time fitted to each experimental divided by the initial surface area of the core sample face [42]:

$$R=\frac{1}{\left(1-\varphi \right)A_{core}}\frac{d{C}_A}{dt}$$

(6)

where R is the dissolution rate of calcite in acid per unit area (mole/cm²·s), C_A is the concentration of the substance A (calcium, in our case), t is the time (s), A_core is the rock sample surface area exposed to acid (cm²), and ϕ is the rock sample porosity (fraction). For all the used samples, the rock surface area to be exposed to the reaction was polished using sandpaper to reduce the error of surface area estimation. If the reaction is limited by the mass transfer of the reactants or the products, increasing $\omega$ increases the mass transfer and, in turn, the dissolution rate will increase. If the mass transfer rate is higher than the rate of acid consumption on the rock surface, the overall dissolution is independent of $\omega$ and the regime is surface reaction limited [43].

4. Materials and Methodology

4.1. Rock Samples and Fluids

Acidizing treatments usually target low permeability zones due to formation damage in the near wellbore. Usually formation damage occurs after starting production and obtaining core samples from a completed well is very difficult if not impossible. In addition, long samples are needed for coreflooding to be able to accurately detect the pressure drop across the sample and define the wormhole breakthrough. Having this in mind, we screened many Indiana limestone samples and selected the samples with low permeability for both the reaction kinetics and coreflooding experiments so that the experimental results can be interpreted and integrated from both rotating disk and coreflooding. Austin chalk samples were selected as they have almost 100% CaCO₃ mineralogy similar to Indiana limestone while having different facies compared to Indiana limestone. In all experiments 20 wt% GLDA was used for the reasons mentioned in Section 2 in this paper.

4.2. Methodology

To study the reaction kinetics of both 20 wt% GLDA/DI and 20 wt% GLDA/SW, a HPHT rotating disk apparatus (Figure 3) was used. The RDA system was designed inhouse at king Fahd university of Petroleumand Minerals and assembled by Hi-Tech Engineering, Morbi, Gujarat, India. The system was designed to allow collecting consecutive samples at a certain time step from the bulk solution during stirring a rock sample at a fixed angular velocity inside the stimulation fluid under HPHT. Additionally, the design allows the contact between the rock sample and the fluid only at the face of the rock by using a harsh environment shrinkage tube which attaches the rock to the rotating disk and also covers all the sides of the sample except the front face of the rock sample. The RDA and the experimental details were comprehensively described in our previous paper [44]. During each experiment, the flux (J_mt) is determined from the analysis of the measured calcium ions concentration in the collected samples. The experiment is then repeated at different angular velocities with all other parameters constant (i.e., temperature and acid concentration).

The approach for defining the limiting step for the reaction of 20 wt% GLDA chelating agent at 3.8 pH solution with carbonate rock is shown in Figure 4. The calcium concentration in ppm is plotted versus time for each angular velocity. The limiting step of the reaction is determined by plotting the dissolution rate (slope of calcium concentration curve versus time) versus the square root of the disk angular velocity for each rock/fluid system at a fixed temperature. A constant slope indicates a mass transfer limited reaction with slow diffusion of reactants and products compared to a zero slope in case of surface reaction limited dissolution where the diffusion of reactants and products is much faster than the dissolution reaction at the rock surface.

5. Experimental Work

5.1. Rock Samples Preparation

Both Indiana limestone and Austin chalk core samples of 0.8-inch-long, 1.5-inch diameter were used. For each sample, the faces were polished to assure a smooth surface for reaction using end face grinding, polishing, and sonic cleaning. The porosity of each sample was calculated using dry and saturated weights.

5.2. RDA Experiments

Two sets of experiments were designed to study the dissolution rate of carbonate rock using GLDA using RDA. In one set, the stock GLDA concentration of 40 wt% was diluted using deionized water was to 20 wt% at (3.8 pH). While on the other set of experiments synthetic gulf water with the composition listed in

Table 2. Synthetic gulf water composition [44].

Ions	Concentration (mg/L)
Sodium	18,300
Calcium	650
Magnesium	2110
Sulfate	4290
Chloride	32,200
Carbonate	0
Bicarbonate	120
Total dissolved salts (TDS)	57,670

was used to dilute GLDA to 20 wt%.

For each set, four experiments were carried out constant pressure (1000 psi), temperature, and different disk rotational speeds (500, 1000, 1500, and 2000 RPM). A 500 mL of the chelating agent at final concentration (20 wt%) was used in each experiment. The density and viscosity of 20 wt% of GLDA/DI and GLDA/SW as a function of temperature are shown in Figure 5. These properties are required when Equation (3) is to be applied. The experimental sets where repeated at different temperatures in the same way (

Table 3. Experiments using GLDA with Indiana limestone and Austin chalk calcite roks.

Experiment No.	Fluid/Rock	Temperature (°F)	Disk Porosity (%)	Disk Angular Velocity (RPM)
1	20 wt% GLDA/DI/Indiana Limestone	150	6.82	500
2			6.82	1000
3			7.07	1500
4			7.15	2000
5		200	10.02	500
6			9.62	1000
7			10.14	1500
8			9.20	2000
9		250	9.08	500
10			9.99	1000
11			6.75	1500
12			9.46	2000
13	20 wt% GLDA/SW with Indiana Limestone	150	12.41	500
14			9.42	1000
15			9.75	1500
16			9.43	2000
17		200	9.30	500
18			9.55	1000
19			9.66	1500
20			6.916	2000
21		250	9.24	500
22			9.53	1000
23			9.53	1500
24			12.41	2000
25	20 wt% GLDA/SW with Austin Chalk	200	26.07	500
26			22.45	1000
27			27.96	1500
28			26.79	2000

). Experiments 1–24 were done for the comparison of DI to seawater on Indiana limestone at 150–250 °F. Experiments 17–20 and experiments 25–28 were carried out for comparison of Indiana limestone to Austin chalk using GLDA/SW system at 200 °F. During each experiment, ten liquid samples of 3 mL volume were collected at a time interval of two minutes. An inductively-coupled plasma optical emission spectroscopy (ICP-OES) Optima 8000 model by PerkinElmer, Waltham, Massachusetts, United States was used to measure the calcium concentration in each sample.

6. Results and Discussion

6.1. Indiana Limestone

The analysis of the first four experiments (Figure 6a) shows that the reaction regime for the 20% GLDA/DI and Indiana limestone rock samples is surface reaction limited at 150 °F. Increasing the temperature from 150 °F to 200 °F increased the surface reaction and turned the reaction to be mass transfer limited regime (Figure 6b). The same temperature effect is also obvious at 200 °F (Figure 6c). Figure 6d summarizes the results of 20% GLDA/DI reaction with Indiana limestone core samples at 150, 200, and 250 °F.

Applying Equation (3), diffusion coefficients of 4.59 × 10⁻⁶ and 1.07 × 10⁻⁵ cm²/s are obtained at 200 and 250 °F respectively. On the other hand, the reaction of 3.8 pH, 20 wt% GLDA/SW with Indiana limestone core samples is mass transfer limited regime at all temperatures (150, 200, and 250 °F) as shown in Figure 7a–d. This is attributed to the high mass transfer resistance due to high salinity. Applying Equation (7), diffusion coefficients of 8.31 × 10⁻⁷, 3.3712 × 10⁻⁶, and 4.71029 × 10⁻⁶ cm²/s are obtained at 150, 200, and 250 °F, respectively. The diffusion coefficient in case of GLDA/SW is smaller compared to GLDA/DI because the chemical species diffusion is buffered by the salts presents in GLDA/SW system. The relation between the effective diffusion coefficient and temperature (Equation (7)) is obtained by fitting a linear equation to the black dashed straight line in Figure 8.

$$D_e=3.88\times {10}^{-8}T-4.79\times {10}^{-6}$$

(7)

Equation (7) is based on three data points for seawater covering the temperature range from 150–250 °F. The Temperature increase in the case of GLDA/DI from 200 to 250 °F highly significantly increased D_e. The reduction in acid diffusion can be attributed to the high calcium concentration chelated in the solution. This acts as a restriction and slowed down the diffusion of GLDA making the mass transfer is the limiting step. By comparing the rate of reaction of the two fluids with Indiana limestone at different RPM, the overall reaction of GLDA with the rock surface is inhibited with the presence of salt ions from seawater in the GLDA/SW solution. In addition, multivalent cations affect the diffusion coefficient. It has been proved that both Mg²⁺ and Ca²⁺ affect the H⁺ diffusion and will retard the reaction rate, which will enforce deep acid penetration as follows [15]:

$$D_{\left(H^{+}\right)}=EXP\left\{\begin{array}{c}\left(\frac{2918.54}{T}\right)-0.589\sqrt{\frac{\left[C{a}^{2+}\right]}{\left[H^{+}\right]}}\\ -0.789\sqrt{\frac{\left[M{g}^{2+}\right]}{\left[H^{+}\right]}}+0.452\left[H^{+}\right]-4.995\end{array}\right\}$$

(8)

Mg²⁺ and Ca²⁺ will retard the reaction in two ways; the first one is according to the previous equation and the second one is that both Mg²⁺ and Ca²⁺ will increase the GLDA viscosity and this will reduce the acid diffusion.

The scanning electron microscopy (SEM) images for the Indiana limestone samples from experiments at same RPM showed that GLDA/DI mainly reacted only with fine grains in the rock surface while GLDA/SW reacted with both fine and coarse grains and made the reaction more uniform at the rock surface (Figure 9). Decreasing the acid diffusion hinders the acid spending process and allows fresh acid to deeply penetrate the rock matrix more uniformly. Based on this, GLDA/SW system can stimulate cores in less injected acid volume at lower injection rate compared to GLDA/DI system. A coreflooding study is required to validate this conclusion.

6.2. Austin Chalk

Four experiments were carried out using Austin chalk samples at 200 °F in the same way described at similar conditions to Indiana limestone sample using GLDA/SW fluid system. The results are shown in Figure 10. From the behavior of the reaction rate versus the square root of the disk angular velocity, it is clear that the reaction regime is mass transfer limited with a reaction diffusion coefficient of 3.96 × 10⁻⁵ cm²/s. The measured diffusion coefficient is higher for Austin chalk case. It’s almost an order of magnitude higher than the diffusion coefficient in the case of reaction with Indiana limestone at the same conditions. With the fact that both Indiana limestone and Austin chalk are chemically composed of almost 100% calcium carbonate, the difference in reaction rates (Figure 11) can be attributed to the pore system geometry and to the bond between the rock grains. The unconfined compressive strength of Indiana limestone is about 5000 psi compared to about 3000 psi in case of Austin chalk. The chelating agent leached more calcite from the Austin chalk samples than the Indiana limestone samples. This effect cannot be captured if only marble was used.

Contrast resulted from different atomic number elements and their distribution is displayed by scanning electron microscopy (SEM). The effect of the acid system on the surface morphology of Austin chalk and Indiana limestone carbonate rocks used in this study is shown in Figure 12.

Indiana limestone, as a bioclastic coarse grained, cemented, and mechanically compacted calcite rock, is less reactive than the microgranular fine grained Austin chalk. Thus, it is clear that each calcite rock has to be studied for the reaction kinetics for the selected stimulation fluid. Marble results will not be applicable for other calcite rocks with the same porosity and permeability. It was observed that not only Damkholer and Peclet numbers control the reactions, but also the rock facies (porosity type and strength) play a major role. All the diffusion rates are listed in

Table 4. Diffusion rates from the RDA experiments using GLDA with Indiana limestone and Austin chalk calcite roks.

Fluid/Rock	Temperature (°F)	Diffusion Rates (cm2/s)
20 wt% GLDA/DI/Indiana limestone	150	-
	200	4.59 × 10−6
	250	1.07 × 10−5
20 wt% GLDA/SW/Indiana limestone	150	8.31 × 10−7
	200	3.37 × 10−6
	250	4.71 × 10−6
20 wt% GLDA/SW/Austin chalk	200	3.96 × 10−5

as a summary for the rotating disc experiments.

6.3. Coreflooding Experiments

To estimate the optimum injection rate using GLDA/SW system, several linear corefloods were performed using 3.81 cm (1.5-inch) diameter and 15.24 cm (6-inch) long Indiana limestone samples.

Table 5. Routine properties of the core samples used for coreflooding at 250 °F and 1000 psi back pressure at different injection rates (Q).

Experiment	L (cm)	D (cm)	$\mathit{\varphi }$ (%)	PV (cm3)	K (mD)	Q (cm3/min)
1	14.94	3.81	9.17	15.61	0.30	0.25
2	15.09	3.81	8.30	14.30	0.51	0.5
3	15.02	3.81	10.54	18.06	1.86	1.0
4	15.03	3.81	9.55	16.37	0.75	2.0
5	15.17	3.81	9.51	16.46	0.81	3.0

(L) sample length, (D) sample diameter, ($\varphi$) porosity, (PV) pore volume, K permeability, (Q) flow rate.

shows the experimental parameters and flooding conditions while Figure 13 shows the schematic of the coreflooding set-up used to carry out linear corefloods at reservoir conditions. The coreflooding system used is a multi purpose EOR flooding systems assembled by Vinci, Nanterre, France.

For all the experiments, 3 wt% KCl (potassium chloride) was used to measure liquid permeability at room temperature, then the temperature was increased to 250 °F for six hours to allow temperature equilibration inside the core sample. The desired injection rate was then set (0.25, 0.5, 1.0, 2.0, or 3.0 cm³/min). Once a steady state flow is achieved by having a constant pressure drop between the inlet and the outlet of the core holder, the injected fluid is switched to GLDA/SW. For each coreflood, the injected acid volume is reported in pore volumes at the wormhole breakthrough (PV_BT) corresponding to zero value of the pressure drop indicating the creation of an infinite conductive channel (wormhole) through the rock sample (Figure 14 and Figure 15). From the CT-scans of the rock samples, a dominant wormhole can be seen at injection rates of 0.5 and 1.0 cm³/min. A wider wormhole can be seen at 2.0 cm³/min compared to lower injection rates with more acid volume required to breakthrough. On the other hand, at 3 and 4 cm³/min several wormholes were initiated at the face of the rock but only a single wormhole propagates with acid injection through the entire rock sample. Unlike HCl, one cannot define a sharp optimum concentration for GLDA. Instead, an optimum injection rate range can be defined between 0.5 and 1 cm³/min. Comparing the pore volumes of 20 wt% GLDA/SW required to breakthrough obtained in this study with the coreflooding using 20wt% GLDA/DI [28], it is clear that the seawater had a retarding effect on GLDA which requires more PV to breakthrough in presence of seawater. The retardation effect is very effective at low injection rate where the retention time of the acid inside the rock is high. Thus, there are two competing mechanisms: the first one is the retardation effect by salts and the second one is the injection rate. At higher injection rate, the acid restricted diffusion (due to salts) will lower the GLDA dissolution capacity and in turn, more acid volume is consumed to create the wormhole. While At low injection rates, GLDA will have enough contact time with the rock in addition to retardation effect and this will result in smooth, tiny wormholes.

The pore volumes of 20 wt% GLDA/DI consumed to achieve breakthrough at 0.25 cm³/min is almost twice the consumed volume of 20 wt% GLDA/SW at the same rate (Figure 16).

An X-ray computed tomography (CT) scanner was used to characterize the wormholes at an energy of 135 kW/200 mA and 1.0 mm resolution (Figure 17). For 20 wt% GLDA/SW, the optimum injection rate is between 0.5 and 1.0 cm³/min with thin, less ramified wormholes at minimum pore volumes (PVs) required to breakthrough.

For accurate determination of GLDA optimum injection rate, a normalized pressure drop ratio (PDR) defined by Equation (9) is used. At the optimum injection rate, the minimum injected pore volume is used during the wormhole propagation to achieve the maximum value of pressure drop reduction from the maximum pressure drop encountered during the acid injection. PDR at time t_i is defined as:

$$PD{R}_i=\frac{\Delta p_{max}-\Delta p_i}{\Delta p_{max}}$$

(9)

where ∆p_max is the maximum pressure drop for each injection rate, $\Delta p_i$ is the pressure drop achieved at time t_i. For example, as shown in Figure 18, at an injection rate of 0.5 cm³/min about 2.0 PVs achieved 60% reduction of ∆p_max where 3.0 PVs were required to achieve the same pressure drop reduction at 1.0 cm³/min injection rate, 5.0 PVs at 2.0 cm³/min and 6.0 PVs at 3.0 cm³/min. Based on this, 0.5 cm³/min can be selected as the optimum injection rate because of the earlier achieved PDR at minimum injected PVs compared to other injection rates.

Using the optimum injection rate model to determine the linear optimum injection rate as a function of core length and diffusion coefficient as follows [45]:

$$Q_{opt\_L}=102h_f{L}_{core}{D}_e$$

(10)

where h_f is the heterogeneity factor, which is defined as the ratio of wormhole length to core length, L_core is the core length, cm, and D_e is the diffusion coefficient, cm²/s. For a 6-inches core sample, and 4.71 × 10⁻⁶ cm²/s diffusion coefficient, an optimum injection rate of 0.43 cm³/min is calculated compared to 0.5 cm³/min as obtained from the coreflooding analysis. Based on this, the results of the rotating disk can be extrapolated to different temperature conditions and the optimum injection rate as a function of temperature and core length can be drawn (Figure 19). Figure 19 represents a graphical representation for Equation (10) for 1.5-inches dimeter Indiana limestone and 20 wt% GLDA/SW (pH 3.8) as a function of temperature. For example, if 20 wt% GLDA/SW is to be used to generate the optimum wormhole at 300 °F through a 1.5-inch diameter and 12-inch long rock sample, an injection rate of 1.3 is to be used for that purpose.

7. Conclusions

In this study, the use of seawater as a base for GLDA chelating agent was proved to be efficient for carbonate stimulation. The reaction of the GLDA/seawater was investigated and the following can be concluded from this study:

-

Rock facies (porosity type) as well as rock strength highly affected the reaction kinetics of GLDA with calcite. This means that the kinetics for each reservoir rock should be investigated with the stimulation fluid. The two tested rocks in this study (Indiana limestone and Austin chalk) are almost 100% calcite but they behaved differently at the same conditions of reaction experiments.

-

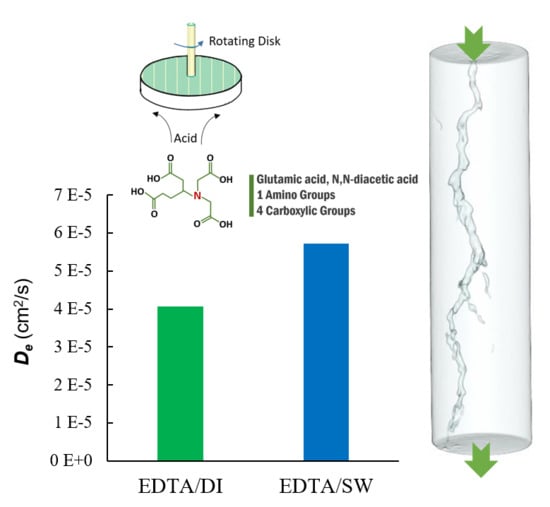
Using seawater to prepare GLDA did not affect the reaction regime at 200 and 250 °F. The reaction regime is limited by mass transfer for both seawater and deionized water based GLDA.

-

The salt content in seawater retarded the reaction when seawater was used as a base for GLDA. The effect was minor at 200 °F and it was prominent at 250 °F. At 250 °F, the GLDA/seawater diffusion coefficient is 50% that in the case of GLDA/deionized water. This is considered as a positive point in the case of GLDA/seawater because it will achieve deep acid penetration due to the retardation effect of the salt in the seawater.

-

A new approach based on dimensionless pore volume to breakthrough, dimensionless time to breakthrough, and the pressure drop ratio was introduced to determine the optimum injection rate in the case of GLDA/seawater stimulation fluid. Unlike HCl and other stimulation fluid, GLDA does not have a sharp optimum injection rate. GLDA has a range for optimum injection rate and the best one can be determined based on the new approach introduced in this study.

-

This study reveals that the rotating disk reaction experiments can be used instead of coreflooding experiments to predict the optimum injection rate in the case of stimulation fluids of mass transfer limited reaction regime.

-

To include the effect of damage length or core length during the coreflooding experiments, more coreflooding experiments are required while a single diffusion coefficient can be used to define the optimum injection rate as a function of core length, which makes the rotating disk approach more convenient in most of the cases. For example, the optimum injection rate predicted from coreflooding was 0.5 cm³/min and that from the rotating disk experiments was 0.43 cm³/min.