Modeling of a PCM TES Tank Used as an Alternative Heat Sink for a Water Chiller. Analysis of Performance and Energy Savings
Abstract
:1. Introduction
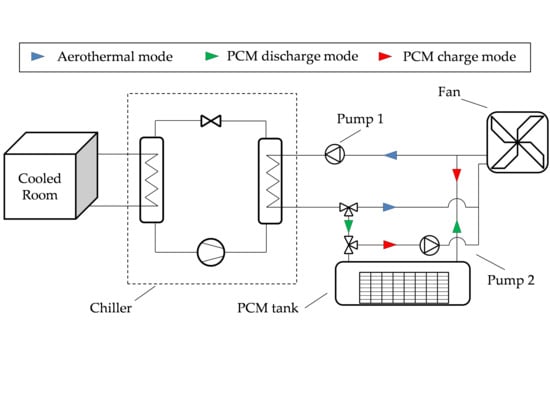
2. Chiller-PCM System Description
3. Model Description and Validation
4. Consumption Analysis
4.1. Operating Modes and Associated Consumptions
4.2. Consumption Analysis of The Different Operating Modes
4.2.1. Consumption Analysis of The Aerothermal Mode
4.2.2. Consumption Analysis of The PCM Discharge Mode
4.2.3. Consumption Analysis of The PCM Charge Mode
4.2.4. Consumption Analysis of The PCM Mode
4.3. Consumption Comparison Between Aerothermal and PCM Modes
4.3.1. Analysis of Energy Savings for Different Values of Tm
4.3.2. Analysis of Energy Savings for Different Values of A
4.3.3. Performance Analysis for Different Use and Temperature Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Daily temperature amplitude (°C) |
| CR | Consumption ratio (-) |
| Cp | Specific heat (kJ·kg−1·K−1) |
| dh | Hydraulic diameter (m) |
| f | Liquid fraction (-) |
| h | Film coefficient (W·m−2·K−1) |
| k | Thermal conductivity (W·m−1·K−1) |
| L | Latent heat (kJ·kg−1) |
| m | Mass (kg) |
| Nu | Nusselt number (-) |
| P | Power (W) |
| Pr | Prandtl number (-) |
| Q | Heat (J) |
| Heat transfer rate (W) | |
| R | Thermal resistance (K·W−1) |
| Ra | Rayleigh number (-) |
| Re | Reynolds number (-) |
| S | Surface (m2) |
| T | Temperature (°C) |
| Tm | Daily mean temperature (°C) |
| Tmelt | Melting temperature (°C) |
| Volumetric flow rate (m3·s−1) | |
| W | Work (J) |
| Greek symbols | |
| δ | Dirac delta function |
| ρ | Density (kg·m−3) |
| Subscripts | |
| aero | Aerothermal mode |
| cnd | Condenser |
| ch | Charge mode |
| comp | Compressor |
| cont | Container |
| dch | Discharge mode |
| ev | Evaporator |
| hz | Homogenization zone |
| in | Inlet |
| liq | Liquid |
| out | Outlet |
| p | Pump |
| sc | PCM section |
| sol | Solid |
| w | Water |
| Abbreviatures | |
| COP | Coefficient of Performance |
| HVAC | Heating, Ventilation and Air-Conditioning |
| PCM | Phase Change Material |
| PID | Proportional Integral Derivative |
| TES | Thermal Energy Storage |
| VCS | Vapor Compression System |
References
- UNFCCC. Kyoto Protocol to the United Nations Framework Convention on Climate Change. In Proceedings of the Third Session of the Conference of the Parties (COP3), Kyoto, Japan, 11 December 1997. [Google Scholar]
- UNFCCC. Adoption of the Paris Agreement; UNFCCC: Bonn, Germany, 2015. [Google Scholar]
- Couloumb, D.; Dupont, J.L.; Pichard, A. 29th Informatory Note on Refrigeration Technologies. The Role of Refrigeration in the Global Economy; International Institute of Refrigeration: Paris, France, 2015. [Google Scholar]
- Couloumb, D.; Dupont, J.L.; Morlet, V. 35th Informatory Note on Refrigeration Technologies. The Impact of the Refrigeration Sector on Climate Change; International Institute of Refrigeration: Paris, France, 2017. [Google Scholar]
- International Energy Agency. Key World Energy Statistics; International Energy Agency: Paris, France, 2017; Available online: https://www.iea.org/publications/freepublications/publication/KeyWorld2017.pdf.
- Seong, Y.B.; Lim, J.H. Energy saving potentials of phase change materials applied to lightweight building envelopes. Energies 2013, 6, 5219–5230. [Google Scholar] [CrossRef]
- Baek, S.; Kim, S. Analysis of thermal performance and energy saving potential by PCM radiant floor heating system based on wet construction method and hot water. Energies 2019, 12, 828. [Google Scholar] [CrossRef]
- Roman, K.K.; O’Brien, T.; Alvey, J.B.; Woo, O.J. Simulating the effects of cool roof and PCM (phase change materials) based roof to mitigate UHI (urban heat island) in prominent US cities. Energy 2016, 96, 103–117. [Google Scholar] [CrossRef]
- Anisur, M.R.; Mahfuz, M.H.; Kibria, M.A.; Saidur, R.; Metselaar, I.H.S.C.; Mahlia, T.M.I. Curbing global warming with phase change materials for energy storage. Renew. Sustain. Energy Rev. 2013, 18, 23–30. [Google Scholar] [CrossRef]
- Canbazoglu, S.; Sahinaslan, A.; Ekmekyapar, A.; Aksoya, Y.; Akarsu, F. Enhancement of solar thermal energy storage performance using sodium thiosulfate pentahydrate of a conventional solar water-heating system. Energy Build. 2005, 37, 235–242. [Google Scholar] [CrossRef]
- Charvát, P.; Klimeš, L.; Zálešák, M. Utilization of an air-PCM heat exchanger in passive cooling of buildings: A simulation study on the energy saving potential in different European climates. Energies 2019, 12, 1133. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Q.; Zhai, Z.J.; Ma, X. Potential of ventilation systems with thermal energy storage using PCMs applied to air conditioned buildings. Renew. Energy 2019, 39–53. [Google Scholar] [CrossRef]
- García, J.P.; Miguez, C.; Monedero, C.; Rico, I. Síntesis del Estudio Parques de Bombas de Calor de España; IDEA: Madrid, Spain, 2014. [Google Scholar]
- Sun, Y.; Wang, S.; Xiao, F.; Gao, D. Peak load shifting control using different cold thermal energy storage facilities in commercial buildings: A review. Energy Convers. Manag. 2013, 71, 101–114. [Google Scholar] [CrossRef]
- Ruddell, B.L.; Salamanca, F.; Mahalov, A. Reducing a semiarid city’s peak electrical demand using distributed cold thermal energy storage. Appl. Energy 2014, 134, 35–44. [Google Scholar] [CrossRef]
- Bruno, F.; Tay, N.H.S.; Belusko, M. Minimising energy usage for domestic cooling with off-peak PCM storage. Energy Build. 2014, 76, 347–353. [Google Scholar] [CrossRef]
- Roth, K.W.; Zogg, R.; Brodrick, J. Emerging technologies: Cool thermal energy storage. ASHRAE J. 2006, 48, 94–96. [Google Scholar]
- Zhao, D.; Tan, G. Experimental evaluation of a prototype thermoelectric system integrated with PCM (phase change material) for space cooling. Energy 2014, 68, 658–666. [Google Scholar] [CrossRef]
- Zhao, D.; Tan, G. Numerical analysis of a shell-and-tube latent heat storage unit with fins for air-conditioning application. Appl. Energy 2015, 138, 381–392. [Google Scholar] [CrossRef]
- PCMProducts Ltd. Available online: http://www.pcmproducts.net/Encapsulated_PCMs.htm (accessed on 9 September 2019).
- Barreneche, C.; Solé, A.; Miró, L.; Martorell, I.; Fernández, A.I.; Cabeza, L.F. Study on differential scanning calorimetry analysis with two operation modes and organic and inorganic phase change material (PCM). Thermochim. Acta 2013, 553, 23–26. [Google Scholar] [CrossRef]
- Dittus, F.; Boelter, L. Heat Transfer in Automobile Radiators of the Tubular Type; University of California Publications in Engineering; University of California Press: Berkeley, CA, USA, 1930; Volume 2, pp. 443–461. [Google Scholar]
- Chiu, J.N.W. Latent Heat Thermal Energy Storage for Indoor Comfort Control. Ph.D. Thesis, KTH School of Industrial Engineering and Management, Stockholm, Sweden, 2013. [Google Scholar]
- Kuznik, F.; Virgone, J.; Johannes, K. Development and validation of a new TRNSYS type for the simulation of external building walls containing PCM. Energy Build. 2010, 42, 1004–1009. [Google Scholar] [CrossRef] [Green Version]
- Mat, S.; Al-Abidi, A.A.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Enhance heat transfer for PCM melting in triplex tube with internal-external fins. Energy Convers. Manag. 2013, 74, 223–236. [Google Scholar] [CrossRef]
- Righetti, G.; Lazzarin, R.; Noro, M.; Mancin, S. Phase Change Materials embedded in porous matrices for hybrid thermal energy storages: experimental results and modelling. Int. J. Refrig. 2019. [Google Scholar] [CrossRef]
- Lazzarin, R.; Noro, M.; Righetti, G.; Mancin, S. Application of hybrid PCM thermal energy storages with and without al foams in solar heating/cooling and ground source absorption heat pump plant: An energy and economic analysis. Appl. Sci. 2019, 9, 1007. [Google Scholar] [CrossRef]















| Parameter | Value |
|---|---|
| Melting temperature (°C) | 27 |
| Density (kg·m−3) | 1530 |
| Specific latent heat (kJ·kg−1) | 150 |
| Specific heat (kJ·kg−1·K−1) | 2.20 |
| Thermal conductivity (W·m−1·K−1) | 0.54 |
| Parameter | Range | R2 Coefficient |
|---|---|---|
| (kW) | [7.37–9.28] | 0.9558 |
| (kW) | [5.70–7.71] | 0.9738 |
| P (kW) | [2.33–3.00] | 0.9912 |
| COP | [1.91–3.31] | 0.9958 |
| Tm (°C). | Day Temperature (Tm+8) (°C) | Night Temperature (Tm−8) (°C) |
|---|---|---|
| 23 | 31 | 15 |
| 25 | 33 | 17 |
| 27 | 35 | 19 |
| 29 | 37 | 21 |
| A (°C) | Day Temperature (25+A) (°C) | Night Temperature (25−A) (°C) |
|---|---|---|
| 6 | 31 | 19 |
| 7 | 32 | 18 |
| 8 | 33 | 17 |
| 9 | 34 | 16 |
| 10 | 35 | 15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Real-Fernández, A.; Navarro-Esbrí, J.; Mota-Babiloni, A.; Barragán-Cervera, Á.; Domenech, L.; Sánchez, F.; Maiorino, A.; Aprea, C. Modeling of a PCM TES Tank Used as an Alternative Heat Sink for a Water Chiller. Analysis of Performance and Energy Savings. Energies 2019, 12, 3652. https://doi.org/10.3390/en12193652
Real-Fernández A, Navarro-Esbrí J, Mota-Babiloni A, Barragán-Cervera Á, Domenech L, Sánchez F, Maiorino A, Aprea C. Modeling of a PCM TES Tank Used as an Alternative Heat Sink for a Water Chiller. Analysis of Performance and Energy Savings. Energies. 2019; 12(19):3652. https://doi.org/10.3390/en12193652
Chicago/Turabian StyleReal-Fernández, Antonio, Joaquín Navarro-Esbrí, Adrián Mota-Babiloni, Ángel Barragán-Cervera, Luis Domenech, Fernando Sánchez, Angelo Maiorino, and Ciro Aprea. 2019. "Modeling of a PCM TES Tank Used as an Alternative Heat Sink for a Water Chiller. Analysis of Performance and Energy Savings" Energies 12, no. 19: 3652. https://doi.org/10.3390/en12193652
APA StyleReal-Fernández, A., Navarro-Esbrí, J., Mota-Babiloni, A., Barragán-Cervera, Á., Domenech, L., Sánchez, F., Maiorino, A., & Aprea, C. (2019). Modeling of a PCM TES Tank Used as an Alternative Heat Sink for a Water Chiller. Analysis of Performance and Energy Savings. Energies, 12(19), 3652. https://doi.org/10.3390/en12193652