Characterization of a Practical-Based Ohmic Series Resistance Model under Life-Cycle Changes for a Lithium-Ion Battery
Abstract
:1. Introduction
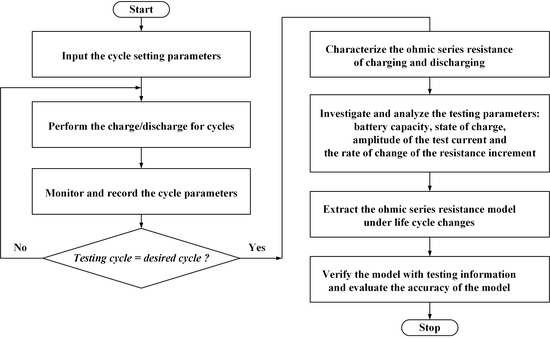
2. Equivalent Circuit Modeling of LIBs and OSR Extraction
3. Characterization of OSR with the Developed Test System
4. Modeling of OSR
4.1. OSR Characteristic of the Cell
4.2. OSR Model under Life-Cycle Consideration
5. Model Verification and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Madani, S.S.; Schaltz, E.; Kaer, S.K. A Review of Different Electric Equivalent Circuit Models and Parameter Identification Methods of Lithium-Ion Batteries. ECS Trans. 2018, 87, 23–37. [Google Scholar] [CrossRef]
- Idaho National Laboratory. Battery Test Manual for Plug-In Hybrid Electric Vehicles; INL/EXT-07-12536 Rev.1; U.S. DOE.: Idaho Falls, ID, USA, 2010; pp. 1–56.
- Huanga, J.; Zhanga, J.; Li, Z.; Song, S.; Wu, N. Exploring Differences between Charge and Discharge of LiMn2O4/Li Half-cell with Dynamic Electrochemical Impedance Spectroscopy. Electrochim. Acta 2014, 131, 228–235. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Baronti, F.; Chow, M.Y. Online Adaptive Parameter Identification and State-of-Charge Coestimation for Lithium-Polymer Battery Cells. IEEE Trans. Ind. Electron. 2014, 61, 2053–2061. [Google Scholar] [CrossRef]
- Rahmoun, A.; Biechl, H. Modelling of Li-ion batteries using equivalent circuit diagrams. Electr. Review ISSN 2012, 88, 152–156. [Google Scholar]
- Zhang, J.; Ci, S.; Sharif, H.; Alahmad, M. Modeling Discharge Behavior of Multicell Battery. IEEE Trans. Energy Conv. 2010, 25, 1133–1141. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Stroe, A.; Swierczynski, M.; Stroe, D.; Teodorescu, R. Performance Model for High-power Lithium Titanate Oxide Batteries based on Extended Characterization Tests. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 6191–6198. [Google Scholar]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint estimation of the electric vehicle power battery state of charge based on the least squares method and the kalman filter algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Kim, D.K.; Muralidharan, P.; Lee, H.W.; Ruffo, R.; Yang, Y.; Chan, C.K.; Peng, H.; Huggins, R.A.; Cui, Y. Spinel LiMn2O4 nanorods as Lithium ion battery cathodes. Nano Lett. 2008, 8, 3948–3952. [Google Scholar] [CrossRef] [PubMed]
- Patil, A.; Patil, V.; Shin, D.W.; Choi, J.W.; Paik, D.S.; Yoon, S.J. Review issue and challenges facing rechargeable thin film Lithium batteries. Mater. Res. 2008, 43, 1913–1942. [Google Scholar]
- Rivera-Barrera, J.P.; Munoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC estimation for lithium-ion batteries: Review and future challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Yuan, H.F.; Dung, L.R. Offline State-of-Health Estimation for High-Power Lithium-Ion Batteries Using Three-Point Impedance Extraction Method. IEEE Trans. Veh. Technol. 2017, 66, 2019–2032. [Google Scholar] [CrossRef]
- Stroe, D.; Swierczynski, M.; Stroe, A.; Kaer, S.K. Generalized characterization methodology for performance modelling of lithium-ion batteries. Batteries 2016, 2, 37. [Google Scholar] [CrossRef]
- Dai, H.; Jiang, B.; Wei, X. Impedance characterization and modeling of lithium-ion batteries considering the internal temperature gradient. Energies 2018, 11, 220. [Google Scholar] [CrossRef]
- Somakettarin, N.; Funaki, T. Study on factors for accurate open circuit voltage characterizations in Mn-type Li-ion batteries. Batteries 2017, 3, 8. [Google Scholar] [CrossRef]
- Somakettarin, N.; Funaki, T. Parameter extraction and characteristics study for manganese-type lithium-ion battery. Int. J. Renew. Energy Res. 2015, 5, 464–475. [Google Scholar]
- Weppner, W.; Huggins, R.A. Determination of the kinetic parameters of mixed-conducting electrodes and application to the system Li3Sb. J. Electrochem. Soc. 1977, 124, 1569–1578. [Google Scholar] [CrossRef]
- Schweiger, H.; Obeidi, O.; Komesker, O.; Raschke, A.; Schiemann, M.; Zehner, C.; Gehnen, M.; Keller, M.; Birk, P. Comparison of several methods for determining the internal resistance of lithium ion cells. Sensors 2010, 10, 5604–5625. [Google Scholar] [CrossRef] [PubMed]
- Somakettarin, N.; Sugihara, H.; Funaki, T. Open-circuit-voltage characterization system design for studies of phase-transition mechanism and deterioration in Mn-type Li-ion batteries. IEICE Electron. Express 2017, 14, 20170690. [Google Scholar] [CrossRef]
- Dubarry, M.; Liaw, B.Y. Identify capacity fading mechanism in a commercial LiFePO4 cell. J. Power Sources 2009, 194, 541–549. [Google Scholar] [CrossRef]









| Description | Specification |
|---|---|
| Cell type | Lithium manganese oxide (LMO) |
| Nominal voltage and capacity | 3.8 V, 3500 mAh |
| Minimum voltage and maximum voltage | 2.90 V–4.25 V |
| Recommended discharge cut voltage (DCV) | 3.00 V |
| Recommended charge threshold voltage (CTV) | 4.20 V |
| Maximum continuous charging current (C-rate) | 1 C (3500 mA) |
| Maximum continuous discharging current (C-rate) | 5.7 C (20,000 mA) |
| Peak discharge current (C-rate) | 7 C (25,000 mA) |
| SOC (%) | Charge | Discharge | ||||
|---|---|---|---|---|---|---|
| OSR0 (mΩ) | kcy (μΩ·cycle−1) | SSR (mΩ2) | OSR0 (mΩ) | kcy (μΩ·cycle−1) | SSR (mΩ2) | |
| 2 | 23.14 | 2.349 | 0.209 | 23.00 | 2.429 | 0.196 |
| 5 | 21.71 | 2.185 | 0.184 | 21.90 | 2.123 | 0.031 |
| 10 | 20.64 | 1.744 | 0.452 | 20.76 | 1.779 | 0.119 |
| 30 | 20.41 | 1.669 | 0.339 | 20.49 | 1.371 | 0.129 |
| 50 | 20.38 | 1.663 | 0.179 | 20.48 | 1.387 | 0.151 |
| 70 | 20.34 | 1.671 | 0.124 | 20.32 | 1.458 | 0.010 |
| 90 | 20.85 | 1.393 | 0.053 | 20.41 | 1.431 | 0.035 |
| 99 | 20.99 | 1.488 | 0.114 | 20.93 | 1.461 | 0.040 |
| Operation Test | k1 (cycle·mΩ−1% −1) | k2 (cycle·mΩ−1) | SSR (mΩ2·cycle) |
|---|---|---|---|
| Charge | 6.3045 × 10−2 | 3.8016 × 10−1 | 7.1380 × 10−2 |
| Discharge | 8.4867 × 10−2 | 3.5265 × 10−1 | 7.0575 × 10−2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somakettarin, N.; Pichetjamroen, A. Characterization of a Practical-Based Ohmic Series Resistance Model under Life-Cycle Changes for a Lithium-Ion Battery. Energies 2019, 12, 3888. https://doi.org/10.3390/en12203888
Somakettarin N, Pichetjamroen A. Characterization of a Practical-Based Ohmic Series Resistance Model under Life-Cycle Changes for a Lithium-Ion Battery. Energies. 2019; 12(20):3888. https://doi.org/10.3390/en12203888
Chicago/Turabian StyleSomakettarin, Natthawuth, and Achara Pichetjamroen. 2019. "Characterization of a Practical-Based Ohmic Series Resistance Model under Life-Cycle Changes for a Lithium-Ion Battery" Energies 12, no. 20: 3888. https://doi.org/10.3390/en12203888
APA StyleSomakettarin, N., & Pichetjamroen, A. (2019). Characterization of a Practical-Based Ohmic Series Resistance Model under Life-Cycle Changes for a Lithium-Ion Battery. Energies, 12(20), 3888. https://doi.org/10.3390/en12203888