Modeling and Controlling of Temperature and Humidity in Building Heating, Ventilating, and Air Conditioning System Using Model Predictive Control
Abstract
:1. Introduction
1.1. Related Works
1.2. Motivation
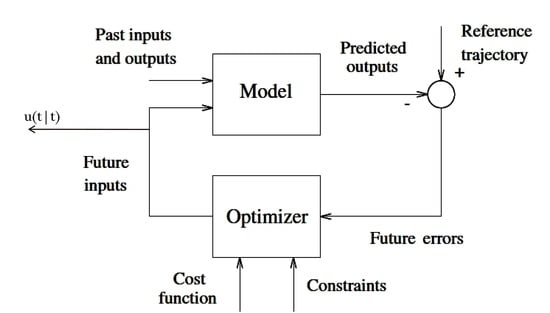
2. Predictive Control Method
- At time : Solve an optimal control problem over a future horizon of steps;
- Apply only the first optimal move , throw the rest of the sequence away;
- At time : Get new measurements and repeat the optimization.
- Objective: Make the output track a reference signal ;
- Idea: Parameterize the problem using input increments as follows:
- Extended system: is as follows:
3. Problem Statement and Formulation
3.1. Predictive Approach to Controlling Temperature and Humidity
3.2. Modeling the Temperature and Humidity of the Room
- Heat generated by the people in the room, lighting equipment, and other devices;
- Heat transferred through the internal walls (the temperature of the internal walls is affected by the heat transfer between the wall and the air inside the room and the solar thermal gain);
- Heat exchanged between the air inside and outside the room through external walls and glass windows;
- Heat produced by air conditioners and natural ventilation;
- Heat stored in the air inside the room.
- Moisture produced by people in the room;
- Moisture produced by a humidifier or air conditioner;
- Humidity stored in the air inside the room.
3.2.1. The Basic Concept of Heat Transfer and Thermodynamics
3.2.2. Mathematical Description of the Thermal and Moisture Dynamics of the Building
3.2.3. Study of Physical Equations for Temperature and Humidity Governing the Room
4. Algorithm Design
4.1. The Predictive Horizon, Horizons of Control and Constraints
- State space prediction model:
- Constraints to enforce:
- Constrained optimal control problem (quadratic performance index):
- Constraints is considered for optimization as follow:
4.2. Cost Function
Weighting Matrix
4.3. Proportional Integral Controller
5. Results of Computational Experiments
5.1. Proportional Integrator Controller
5.2. Predictive Model Control
6. Conclusions
- The presentation of the modeling strategy was done in a completely transparent and precise manner, and it was possible to extract it for all other buildings. Due to the presence of room humidity as another effective parameter to ensure residents’ comfort, a dynamic model was presented to analyze the performance. Following that, the MPC structure was proposed to control the temperature and humidity inside the room with minimal trace error and control effort in the form of a multi-objective optimization problem;
- Simulation results were compared and proved that the performance of the MPC was improved. The MPC controller had a better transient response to control the temperature and relative humidity of the intake air and further increased in the presence of disturbances inside and outside the environment;
- During the setting of the low-flow-rate set point, the PI controller produced a slow response that required extra time to reach the setting point. For a high-flow rate set point, the PI response was high, resulting in an excessive gain from the adjustment point. In contrast, the MPC in both cases produced stable responses and reduced the time for the meeting to be faster and more efficient;
- The control effort employed by PI was bigger than the control effort generated by the MPC. By assessing the control signal generated by the PI and the probe control, it was observed that under low-load cooling loads, a large PI produced an oscillatory control signal that needed to be reset. In front of the MPC, a very soft control signal produced both low and high cooling conditions;
- The PI adjusted the region temperature individually in multiple building areas without exchanging information with neighboring controllers. However, the MPC considered the impacts of adjacent neighborhoods’ interaction by providing predictions of these interaction impacts and relation to control decisions with adjacent controller. The MPC adjusted the level of comfort to the desired air-conditioning level that was appropriate for those in the areas with multiple occupations, while the PI maintained the desired thermal comfort with regard to the number of occupancies that increased in each area with failure. In order to control the temperature and humidity of the room, the MPC controller provided a much better performance over the PI;
- While the MPC used optimization rules at any time of the sampling, it will also be possible to increase the sampling time by up to 10 min, which will increase the lifespan of the operators and the processor. On the other hand, tracking accuracy was also higher in the MPC and was softly achieved with less control effort. The integrator correlator will require a great deal of control to achieve roughly similar tracking results;
- In future research, the amount of carbon dioxide produced in the room should be considered as another important factor in providing comfort condition for residents. Furthermore, future work should estimate the presence of people inside the room as a disturbance in the cost function and attempt to dispose these factors using multi-person tracking via UWB Radars.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Controller Parameters | |
| Desired process output | |
| Control signal | |
| Process actual output | |
| X | States |
| R | Reference signal |
| Sampling time | |
| Weighting matrix of inputs | |
| Weighting matrix of states | |
| Prediction horizon | |
| Control horizon | |
| Cost function | |
| System Parameters | |
| Wall thermal resistivity | |
| Window thermal resistivity | |
| Ceiling thermal resistivity | |
| Door thermal resistivity | |
| Wall thermal conductivity | |
| Window thermal conductivity | |
| Ceiling thermal conductivity | |
| Door thermal conductivity | |
| Room heat capacity | |
| Air specific heat capacity | |
| Southern wall heat capacity | |
| Northern wall heat capacity | |
| Western wall heat capacity | |
| Eastern wall heat capacity | |
| Ceiling heat capacity | |
| Outside air temperature | |
| Southern wall temperature | |
| Northern wall temperature | |
| Western wall temperature | |
| Eastern wall temperature | |
| Roof wall temperature | |
| Room temperature | |
| Average daily sunlight on the south wall | |
| Average daily sunlight on the northern wall | |
| Average daily sunlight on the western wall | |
| Average daily sunlight on the eastern wall | |
| Average daily sunlight on the roof | |
| Door area | |
| Window area | |
| Northern wall area | |
| Southern wall area | |
| Western wall area | |
| Eastern wall area | |
| Roof wall area | |
| Mass flow rate | |
| Room Volume | |
| Room air density | |
| Exhaust air density | |
| Source air density | |
| Room humidity ratio | |
| Exhaust humidity ratio | |
| Source humidity ratio | |
| Air changes per hour | |
| Thermal disturbances | |
| Moisture disturbances | |
| Abbreviation | |
| MPC | Model Predictive Control |
| BMS | Building Management System |
| PI | Proportional integral controller |
| HVAC | Heating, ventilation, and air-conditioning |
| CAV | Constant air volume |
| RC | Resistance Capacitance |
| UWB | Ultra-Wideband |
References
- UN Global Status Report. Towards a Zero-Emission, Efficient, and Resilient Buildings and Construction Sector; UN Global Status Report: Katowice, Poland, 2017; pp. 1–21. [Google Scholar]
- Annual Energy Outlook. Annual Energy Outlook; Energy Information Administration (EIA): Washington, DC, USA, 2012; pp. 1–252. [Google Scholar]
- Mull, T.E. HVAC Principles and Applications Manual; McGraw-Hill: New York, NY, USA, 1998; pp. 1–528. [Google Scholar]
- Jaradat, M. Fuzzy logic controller deployed for indoor air quality control in naturally ventilated environments. J. Electr. Eng. 2009, 12–17. [Google Scholar]
- Chen, W.; Chan, M.; Weng, W.; Yan, H.; Denga, S. An experimental study on the operational characteristics of a direct expansion based enhanced dehumidification air-conditioning system. Appl. Energy 2009, 225, 922–933. [Google Scholar] [CrossRef]
- Chen, W.; Chan, M.; Denga, S.; Yan, H.; Weng, W. A direct expansion based enhanced dehumidification air-conditioning system for improved year-round indoor humidity control in hot and humid climates. Build. Environ. 2018, 139, 95–109. [Google Scholar]
- Gao, J.; Xu, X.; Li, X.; Zhang, J.; Zhang, Y.; Wei, G. Model-based space temperature cascade control for constant air volume air-conditioning system. Build. Environ. 2018, 145, 308–318. [Google Scholar] [CrossRef]
- Chen, Y.; Norford, L.K.; Samuelson, H.W.; Malkawi, A. Optimal Control of HVAC and Window Systems for Natural Ventilation Through Reinforcement Learning. Energy Build. 2018, 169, 1–23. [Google Scholar] [CrossRef]
- Shiyu, Y.; Pun, W.M.; Feng, N.B.; Tian, Z.; Babu, S.; Zhe, Z.; Wanyu, C.; Dubey, S. A State-Space Thermal Model Incorporating Humidity and Thermal Comfort for Model Predictive Control in Buildings. Energy Build. 2018, 170, 1–39. [Google Scholar]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Sangaiah, A. Spatial and Semantic Convolutional Features for Robust Visual Object Tracking. Multimed. Tools Appl. 2018, in press. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Y.; Feng, W.; Wang, J. Spatially attentive visual tracking using multi-model adaptive response fusion. IEEE Access 2019, 7, 83873–83887. [Google Scholar] [CrossRef]
- Xia, Z.Q.; Fang, Z.W.; Zou, F.F.; Wang, J.; Sangaiah, A.K. Research on defensive strategy of real-time price attack based on multiperson zero-determinant. Secur. Commun. Netw. 2019, 2019, 6956072. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Dai, L.Z.; Bian, H.B.; Ma, Y.F.; Zhang, J.R. Concrete cracking prediction under combined prestress and strand corrosion. Struct. Infrastruct. Eng. 2019, 15, 285–295. [Google Scholar] [CrossRef]
- Chen, Z.; Quan, W.; Wen, M.; Fang, J.; Yu, J.; Zhang, C.; Luo, L. Deep Learning Research and Development Platform: Characterizing and Scheduling with QoS Guarantees on GPU Clusters. IEEE Trans. Parallel Distrib. Syst. 2019, in press. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Lu, C.; Wang, J.; Sangaiah, A. Lightweight deep network for traffic sign classification. Ann. Telecommun. 2019. [Google Scholar] [CrossRef]
- He, S.; Li, Z.; Tang, Y.; Liao, Z.; Wang, J.; Kim, H.-J. Parameters compressing in deep learning, computers. Mater. Contin. 2019, 13, 45–53. [Google Scholar]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Li, K. Dual Model Learning Combined with Multiple Feature Selection for Accurate Visual Tracking. IEEE Access 2019, 7, 43956–43969. [Google Scholar] [CrossRef]
- Hannan, M.A.; Faisal, M.; Ker, P.J.; Mun, L.H.; Parvin, K.; Mahlia, T.M.I.; Blaabjerg, F. A Review of Internet of Energy Based Building Energy Management Systems: Issues and Recommendations. IEEE Access 2018, 6, 1–18. [Google Scholar]
- Tushar, W.; Wijerathne, N.; Li, W.; Yuen, C.; Poor, H.V.; Saha, T.K.; Wood, K.L. Internet of Things for Green Building Management. IEEE Signal Process. Mag. 2018, 35, 100–110. [Google Scholar] [CrossRef]
- Okaeme, C.C.; Mishra, S.; Wen, J.T. Triggering and Control Co-design in Self-Triggered Model Predictive Control of Constrained Systems: With Guaranteed Performance. IEEE Trans. Control Syst. Technol. 2018, 63, 1–12. [Google Scholar]
- Okaeme, C.C.; Mishra, S.; Wen, J.T. Passivity-Based thermohygrometric Control in Buildings. IEEE Trans. Control. Syst. Technol. 2018, 26, 1–12. [Google Scholar] [CrossRef]
- Cao, N.; Ting, J.; Sen, S.; Raychowdhury, A. Smart sensing for HVAC control: Collaborative intelligence in optical and IR cameras. IEEE Trans. Ind. Electron. 2018, 65, 1–9. [Google Scholar] [CrossRef]
- Dhar, N.K.; Verma, N.K.; Behera, L. Adaptive Critic based Event-Triggered Control for HVAC System. IEEE Trans. Ind. Inform. 2018, 14, 1–10. [Google Scholar] [CrossRef]
- Ruddy, J.; Meere, R.; Loughlin, C.O.; Donnell, T.O. Design of VSC Connected Low-Frequency AC Offshore Transmission with Long HVAC Cables. IEEE Trans. Power Deliv. 2017, 33, 1–10. [Google Scholar] [CrossRef]
- Wei, F.; Li, Y.; Sui, Q.; Lin, X.; Chen, L.; Chen, Z.; Li, Z. A Novel Thermal Energy Storage System in Smart Building Based on Phase Change Material. IEEE Trans. Smart Grid 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Yu, L.; Xie, D.; Huang, C.; Jiang, T.; Zou, Y. Energy Optimization of HVAC Systems in Commercial Buildings Considering Indoor Air Quality Management. IEEE Trans. Smart Grid 2018, 99, 1–11. [Google Scholar] [CrossRef]
- Homod, R.Z. Analysis and Optimization of HVAC Control Systems Based on Energy and Performance Considerations for Smart Buildings. Renew. Energy 2018, 126, 1–43. [Google Scholar] [CrossRef]
- Alez-Prieto, I.G.; Duran, M.J.; Garcia, N.R.; Barrero, F.; Mart´ın, C. Open-Switch Fault Detection in Five-Phase Induction Motor Drives Using Model Predictive Control. IEEE Trans. Control. Syst. Technol. 2018, 65, 3045–3055. [Google Scholar]
- Lucia, S.; Navarro, D.; Lucia, O.; Zometa, P.; Findeisen, R. Optimized FPGA Implementation of Model Predictive Control for Embedded Systems Using High-Level Synthesis Tool. IEEE Trans. Ind. Inform. 2018, 14, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Norambuena, M.; Rodriguez, J.; Zhang, Z.; Wang, F.; Garcia, C.; Kennel, R. A Very Simple Strategy for High-Quality Performance of AC Machines Using Model Predictive Control. IEEE Trans. Power Electron. 2018, 34, 1–7. [Google Scholar] [CrossRef]
- Rostami, S.M.H.; Ghazaani, M. State-dependent Riccati equation tracking control for a two-link robot. J. Comput. Nanosci. 2018, 15, 1490–1494. [Google Scholar] [CrossRef]
- Rostami, S.M.H.; Sangaiah, A.K.; Wang, J.; Kim, H.J. Real-time obstacle avoidance of mobile robots using state-dependent Riccati equation approach. EURASIP J. Image Video Process. 2018, 79, 1–13. [Google Scholar] [CrossRef]
- Rostami, S.M.H.; Ghazaani, M. Design of a Fuzzy controller for Magnetic Levitation and compared with Proportional Integral Derivative controller. J. Comput. Theor. Nanosci. 2018, 15, 3118–3125. [Google Scholar] [CrossRef]
- Ghazaani, M.; Rostami, S.M.H. An Intelligent Power Control Design for a Wind Turbine in Different Wind Zones Using FAST Simulator. J. Comput. Theor. Nanosci. 2019, 16, 25–38. [Google Scholar] [CrossRef]
- Rostami, S.M.H.; Sangaiah, A.K.; Wang, J.; Liu, X. Obstacle Avoidance of Mobile Robots Using Modified Artificial Potential Field Algorithm. EURASIP J. Wirel. Commun. Netw. 2019, 70, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Gao, Y.; Yin, X.; Li, F.; Kim, H.J. An enhanced PEGASIS algorithm with mobile sink support for wireless sensor networks. Wirel. Commun. Mob. Comput. 2018, 2018, 9472075. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Wu, W.B.; Lim, S. An asynchronous clustering and mobile data gathering schema based on timer mechanism in wireless sensor networks. Comput. Mater. Contin. 2019, 58, 711–725. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Xie, K.; Xie, K.; Xu, C.; Jin, W. Interference-aware multi-source transmission in multi-radio and multi-channel wireless network. IEEE Syst. J. 2019, 13, 2507–2518. [Google Scholar] [CrossRef]
- He, S.; Xie, K.; Chen, W.; Zhang, D.; Wen, J. Energy-aware routing for SWIPT in multi-hop energy-constrained wireless network. IEEE Access 2018, 6, 17996–18008. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Sangaiah, A.K.; Kim, H.J. An intelligent data gathering schema with data fusion supported for mobile sink in WSNs. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef] [Green Version]
- Salehpour, J.; Radmanesh, H.; Rostami, S.M.H.; Wang, J.; Kim, H.J. Effect of load priority modeling on the size of fuel cell as an emergency power unit in a more-electric aircraft. Appl. Sci. 2019, 9, 3241. [Google Scholar] [CrossRef] [Green Version]
- Ramezani, E.; Rostami, S.M.H. Fast Terminal Sliding-Mode Control with an Integral Filter Applied to a Longitudinal Axis of Flying Vehicles. J. Comput. Theor. Nanosci. 2019, 16, 3141–3153. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Sangaiahand, A.K.; Kim, H.J. Energy Efficient Routing Algorithm with Mobile Sink Support for Wireless Sensor Networks. Sensors 2019, 19, 1494. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Kelman, A.; Daly, A.; Borrelli, F. Predictive control for energy efficient buildings with thermal storage: Modeling, stimulation, and experiments. IEEE Control Syst. Mag. 2012, 32, 44–64. [Google Scholar]
- Shide, S.; Amin, H. Critical review and research roadmap of office building energy management based on occupancy monitoring. Energy Build. 2019, 182, 214–241. [Google Scholar]
- Gianni, B.; Marco, C.; Daniele, P.; Antonio, V.; Giovanni, G.Z. An integrated Model Predictive Control approach for optimal HVAC and energy storage operation in large-scale buildings. Appl. Energy 2019, 240, 327–340. [Google Scholar]
- Gorjian, S.; Hashjin, T.T.; Ghobadian, B. Estimation of mean monthly and hourly global solar radiation on surfaces tracking the sun: Case study: Tehran. In Proceedings of the IEEE 2012 Iranian Conference on Renewable Energy and Distributed Generation, Tehran, Iran, 6–8 March 2012. [Google Scholar]
- Edalati, S.; Ameri, M.; Iranmanesh, M. Estimating and modeling monthly mean daily global solar radiation on horizontal surfaces using artificial neural networks in south east of Iran. J. Renew. Energy Environ. 2014, 2, 41–48. [Google Scholar]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef] [Green Version]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 85th ed.; CRC Press: Washington, DC, USA, 2004; pp. 1–130. [Google Scholar]
- ASHRAE-Handbook-Fundamentals, American Society of Heating, Refrigerating and Air-Conditioning Engineers. 2018, pp. 1–122. Available online: https://www.ccacoalition.org/en/partners/american-society-heating-refrigerating-and-air-conditioning-engineers-ashrae (accessed on 22 November 2019).
- Rostami, S.M.H.; Alimohammadi, V. Fuzzy Decentralized Controller Design with Internet of Things for Urban Trains. Adv. Sci. Eng. Med. 2020, 12, 421–432. [Google Scholar]
- Riahifard, A.; Rostami, S.M.H.; Wang, J.; Kim, H.J. Adaptive Leader-Follower Formation Control of Under-actuated Surface Vessels with Model Uncertainties and Input Constraints. Appl. Sci. 2019, 9, 3901. [Google Scholar] [CrossRef] [Green Version]



















| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 5.77 σ | 111.3 kwh/m2 | ||
| 2.31 σ | 101.1 kwh/m2 | ||
| 3.26 σ | 155.2 kwh/m2 | ||
| 3.18 σ | 158.2 kwh/m2 | ||
| 72 kJ/K | 303.1 kwh/m2 | ||
| 1.005 kJ/K | 10 °C | ||
| 5644 kJ/K | 70 kg/kg | ||
| 6773 kJ/K | 1.2 kg/m3 | ||
| 6450 kJ/K | 2.4 m2 | ||
| 6450 kJ/K | 4.5 m2 | ||
| 10750 kJ/K | 12.6 m2 | ||
| 0.453 kg/h | 10.5 m2 | ||
| 60 m3 | 12 m2 | ||
| 2 h−1 | 12 m2 | ||
| 20 m2 |
| Controller | Sampling Time | Calculation Time | |||
|---|---|---|---|---|---|
| PI | 1 s | 5.3122 s | 31.8931 | 0.7883 | 399.8990 |
| 45 s | 6.5039 s | 25.2538 | 0.7774 | 461.8423 | |
| MPC | 45 s | 197.4863 s | 11.7213 | 0.6342 | 341.1243 |
| 10 min | 25.6737 s | 574.771 | 16.8167 | 423.2184 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahramnia, P.; Hosseini Rostami, S.M.; Wang, J.; Kim, G.-j. Modeling and Controlling of Temperature and Humidity in Building Heating, Ventilating, and Air Conditioning System Using Model Predictive Control. Energies 2019, 12, 4805. https://doi.org/10.3390/en12244805
Bahramnia P, Hosseini Rostami SM, Wang J, Kim G-j. Modeling and Controlling of Temperature and Humidity in Building Heating, Ventilating, and Air Conditioning System Using Model Predictive Control. Energies. 2019; 12(24):4805. https://doi.org/10.3390/en12244805
Chicago/Turabian StyleBahramnia, Pouria, Seyyed Mohammad Hosseini Rostami, Jin Wang, and Gwang-jun Kim. 2019. "Modeling and Controlling of Temperature and Humidity in Building Heating, Ventilating, and Air Conditioning System Using Model Predictive Control" Energies 12, no. 24: 4805. https://doi.org/10.3390/en12244805
APA StyleBahramnia, P., Hosseini Rostami, S. M., Wang, J., & Kim, G. -j. (2019). Modeling and Controlling of Temperature and Humidity in Building Heating, Ventilating, and Air Conditioning System Using Model Predictive Control. Energies, 12(24), 4805. https://doi.org/10.3390/en12244805