Design of Robust Total Site Heat Recovery Loops via Monte Carlo Simulation

Abstract

For increased total site heat integration, the optimal sizing and robust operation of a heat recovery loop (HRL) are prerequisites for economic efficiency. However, sizing based on one representative time series, not considering the variability of process streams due to their discontinuous operation, often leads to oversizing. The sensitive evaluation of the performance of an HRL by Monte Carlo (MC) simulation requires sufficient historical data and performance models. Stochastic time series are generated by distribution functions of measured data. With these inputs, one can then model and reliably assess the benefits of installing a new HRL. A key element of the HRL is a stratified heat storage tank. Validation tests of a stratified tank (ST) showed sufficient accuracy with acceptable simulation time for the variable layer height (VLH) multi-node (MN) modelling approach. The results of the MC simulation of the HRL system show only minor yield losses in terms of heat recovery rate (HRR) for smaller tanks. In this way, costs due to oversizing equipment can be reduced by better understanding the energy-capital trade-off.

1. Introduction

In Europe, the food and beverage industry is the fifth largest energy consumer [1], consuming the highest share of low-temperature heat demand of the total process heat demand [2]. Using renewable energies and increasing energy efficiency are ways to reduce greenhouse gas (GHG) emissions [3]. First, the potential to reduce process energy demand can be identified using process integration methods [4]. If the possibilities of increasing the energy efficiency at the process level through direct heat recovery are exhausted, further energy saving is possible by means of total site heat integration [5], with a specific focus on low-temperature processes [6] and heat recovery loops (HRL) [7].

In many industries, such as the dairy and beverage industry, the individual processes are operated non-continuously for product changes and cleaning reasons. This poses additional challenges to heat recovery, often requiring the use of energy storage. Two approaches to characterizing batch processes and its flows are the time average model (TAM) and the time slice model (TSM). The TAM indicates heat recovery potential, which can be achieved by indirect heat transfer and storage based on an HRL. Olsen et al. [8] present a systematic thermal energy storage integration method based on the TAM approach. Their indirect source and sink profile (ISSP) method enables the concrete identification of suitable sink and source profiles and the dimensioning of intermediate circuits and heat storage [9]. Due to the integration of multiple sink and source streams, the utilization of the storage capacity increases the overall availability and performance of sources and sinks. For sensible heat storage, there are closed stratified tanks (ST) and fixed temperature variable mass (FTVM) open storage tanks. FTVM tanks require a larger storage volume than ST tanks, but they are easier to operate and suitable for very large circulating volumes and small temperature differences. ST tanks need only half the volume and can operate at temperatures above 100 °C when placed under pressure. Due to the temperature dependency of fluid density, higher temperature fluid (lower density) forms a hot zone at the top of the tank, while lower temperature fluid forms one at the bottom. These zones are separated by a narrow transition area (between h_Tu and h_Tl)—the thermocline. For varying source and sink streams, the volume of fluid in each temperature zone increases or decreases, moving the thermocline vertically within the storage tank (see Figure 1). A completely loaded or unloaded storage tank, in addition to other mixing effects, results in a loss of stratification, loss of heat recovery, and even temporary shutdown of the HRL [10].

Dynamic simulation is necessary for evaluating and proving the performance of an HRL system in any scenario. This is due to arbitrary production and logistic timing, the changing operation time of process states, thermal inertias, as well as dynamic interaction. Past models have focused on either the heat recovery side of the HRL [11] or the ST unit. These models assumed that there was a perfect interface between the cold and hot area of the ST [12], which is a simplification of practical installations. Walmsley et al. [13] studied an experimental scale model of an industrial ST, including the interaction between flows and thermocline movement and growth, but did not incorporate this element into their HRL models. The growth and movement of the thermocline accelerate the loss of stratification, reducing the effective heat recovery capacity of the tank over time and leading to reduced energy savings. Baeten et al. [14] presented a model that incorporates the buoyancy and mixing in one-dimensional stratified storage tanks in building energy simulations to estimate the uncertainty of parameters as a function of the storage capacity caused by the storage tank model. Campos Celador et al. [15] showed that the storage tank model used in such simulations can have major effects on calculated annual savings and design decisions. Powell and Edgar [16] introduced an adaptive-grid model with a high-resolution grid in the region of thermal stratification. This ensures higher accuracy and simulation performance than other one-dimensional models, and has speed advantages over computational fluid dynamics (CFD) models in repetitive simulations (e.g., for optimization, validation, control, prediction). Schlosser et al. [17] demonstrated a multi-node (MN) approach can represent a good compromise between accuracy and simulation time for the high-fidelity simulation of HRL systems. Numerical diffusion errors were reduced by approximately 35% using a variable layer height (VLH) model. The stratification of the physical thermocline growth could be re-established while still operating the ST by siphoning the mixed thermocline area from the tank [13]. Furthermore, a control system consisting of a single flow and system control for maintaining stratification was applied. The system control operated depending on the thermocline position, enabling restratification after being completely charged or discharged and a single flow control adjusted the individual streams to the target temperatures $T_{hot}$ or $T_{cold}$. This previous simulation study [17] included a typical week of production for tank sizing and evaluation, taking no account of stochastic changes (e.g., order quantity) or deterministic influences, such as recipe sequences. As an extension, the present work simulates several weeks of production, based on synthetic time series with probabilistic influence (e.g. changing recipes and order amounts) by Monte Carlo (MC) simulation to generate a sensitivity evaluation of the HRL system. Atkins et al. [10] highlighted the optimal sizing of an ST as a prerequisite for economic efficiency and operability. Moreover, Meschede et al. [18] applied MC methods to highlight the risk caused by using a single reference time series for designing energy systems. The MC method helps to define the mean of the heat recovery rate (HRR) for different tank sizes more precisely, and to better assess the risk of fluctuating heating and cooling load due to stochastic influences [19]. A prerequisite for this, however, is an accurate and high-performance VLH model.

The aim of the paper is to improve the design and operation of industrial HRLs by constructing a comprehensive model of storage and heat exchanger operations, simulated with a MC approach. Therefore, the first step of this study is to validate the performance and accuracy of the VLH model. Secondly, the effect of the variability of streams on the sizing approach in terms of heat integration potential and operability is evaluated by MC simulation, with real process data from the dairy industry. The MC method considers the sensitivity of stochastic influences (order quantity, sequence of recipes) and deterministic relations (production process: idling, operation, cleaning in place (CIP)) on the volatility of sink and source profiles. The results are probability distributions of the HRR for different storage dimensions of the present case study.

The article essentially contains two objectives: (1) the validation of the accuracy and performance of the VLH multi-node (MN) model and (2) a risk assessment of the robustness of the ST design and control by MC simulation, based on the validated model. The validation of the VLH model, developed by Schlosser et al. [17], is carried out on the basis of the validation experiments introduced by Walmsley [20] in comparison with a real laboratory tank and a CFD model (Section 2.1 and Section 3.1). The simulation of a VLH model-based HRL, designed according to the ISSP method (Section 2.3), is realized by stochastically generated time series as input following the MC approach (Section 3.3). The generation based on cumulative distribution functions (CDF) was developed in the context of this work (Section 2.2) and applied (Section 3.2) for measurement data of a case study [12]. The results of Section 3 are summarized in Section 4.

2. Materials and Methods

The following sections describe the methods for validating the VLH model and the evaluation approach for the HRL dimensioning. The first section presents the different validation experiments proving the accuracy and performance of the VLH model. Subsequently, the generation of stochastic time series based on random influences and deterministic correlations is described. Finally, the evaluation approach of a robust storage sizing based on dynamic simulation is presented.

2.1. Verification and Validation of the Variable Layer Height Model

Verification and validation tests confirm if a model reproduces a certain (physical) behavior qualitatively and quantitatively correct, or with tolerable deviations. In this context, verification means checking whether the model correctly implements the derived equations. Verification can be understood as a qualitative examination of the transformation and the functionality of the model. Validation quantitatively checks the representation of the original system by the model. The quantitatively correct representation of the reference system is determined by subjectively defined tolerances, so that a model can be described as sufficiently accurate within a certain error deviation [21].

The model is examined in two dimensions–performance and accuracy. To calculate a large number of probable time series for a production week in an appropriate time frame, sufficient simulation speed is required. In terms of verification, the functionality is given by using universal physical descriptions. The validation is based on data from a CFD model, which is validated by a lab-scale, insulated ST (6.44 L) made of Perspex [20]. In this way, sufficient accuracy of the VLH model can be demonstrated by various experiments. After the numerical diffusion errors are minimized [17], the position of the thermocline, characterizing the heat recovery capacity, is used as a measure of the error deviation. As a validation quality, the following unitless key metrics are developed. The percentage of ideal cases (PIC) represents the share of the ideal ST case $A_0$ compared to the areas of cold $A_1$ and hot $A_2$ losses of stratification, as illustrated in Figure 2. PIC quantifies the level of stratification. The PIC number is defined as:

$$PIC=1-\frac{A_1+A_2}{\left(\frac{A_0}{2}\right)}$$

(1)

This results in the following operating ranges [20]:

• The tank is perfectly stratified:        $PIC=1$
• The tank is fully mixed, all hot or cold fluid:  $PIC=0$
• The tank is normal operating:         $0\le PIC\le 1$

The position and height of the thermocline $h_{tm}$ gives information about the available heat recovery capacity. The dimensionless height $h_{tm,i}$ of the thermocline is determined by the division of the actual height $h_{tm}$ and the total tank height H. Associated with the thermocline thickness $H_t$ the degradation of the stratification is quantified.

$$H_t=h_{tu}\left(T_{tu}\right)-h_{tl}\left(T_{tl}\right)$$

(2)

This work is now based on the validation parameters of the PIC, characterizing the degree of thermocline degradation. The deviation of the PIC from the experimental values in different experiments is quantitatively assessed. The height of thermocline $h_{tm,i}$ is qualitatively discussed by means of a targeted loading and unloading profile. The following validation measures are conducted. The settings and boundary conditions of each experiment are presented in

Table 1. Settings and boundary conditions of validation.

Number	Validation Experiment	Physical Modelling	${\dot{\mathit{V}}}_{\mathit{i}}$	${\mathit{T}}_{0,\mathit{h}\mathit{o}\mathit{t}}$	${\mathit{T}}_{0,\mathit{c}\mathit{o}\mathit{l}\mathit{d}}$	${\mathit{T}}_{\mathit{a}\mathit{m}\mathit{b}}$	${\mathit{h}}_{0\mathit{t}\mathit{m}}$	${\mathit{H}}_{0\mathit{t}\mathit{m}}$	Simulation Time
			L/min	$°\mathbf{C}$	$°\mathbf{C}$	$°\mathbf{C}$	-	m	min
1a	Static Mode	Adiabatic	-	40	20		0.5	0	200
1b		Non-adiabatic	-	40	20	15	0.5	0	200
2a	Charging	Constant charging with 40 °C	0.15	20	20	15	1.0	0	26.7
2b			0.4						10.0
2c			1.0						4.0
2d			2.0						2.0
3	Movement	Sequentially charging	0.4	40	20	15	0.5	0	25

.

(1)

The Static Mode investigates heat transfer mechanisms during a certain simulation time in a ST, with ideal stratification at the beginning, without inlet or outlet flows, and with (a) and without (b) heat losses. The loss of stratification by the numerical and physical diffusion effects is described by PIC.

(2)

Establishment of the thermocline by Charging studies the effect of the inlet flow rate of a charging process on the level of thermal stratification. In particular, the thermocline thickness and the location are observed. The tank is completely filled with cold water and warm water is supplied with different flow rates.

(2)

Operating Mode Movement studies the effect a changing charging and discharging flow rates on the thermal thermocline position based on $h_{tm}$. Moreover, the degradation of stratification was measured by $\mathrm{PIC}$. The storage tank is alternately loaded and unloaded with 2 L cold, 4 L warm, and again 4 L cold water at a flow rate of 0.4 L/min.

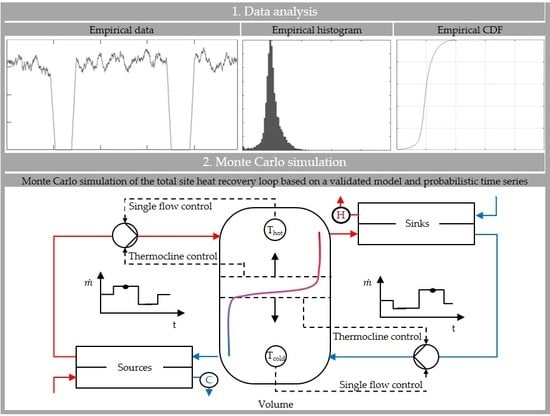
2.2. Generation of Stochastic Time Series for Monte Carlo Simulation

Understanding the variability of the available sources and sinks is prerequisite for an optimized volume of the required thermal storage and to achieve a balanced system. As already outlined, several different factors have an influence on the height and temporal course of the heat source and heat sink processes. Within the framework of a simulation study, reliable and comparable energy savings considering the dynamic system’s behavior, can be calculated. A sensitivity analysis considers the influence of fluctuating factors on the target variables robustness of the HRL dimensioning and HRR. If probabilities are assigned to the stochastic influencing factors, time series that occur with a certain probability can be generated from the deterministic correlations. The generated time series serve as input data for the dynamic simulation. Thus, the simulation validates the resulting heat recovery potential, depending on the tank size, regarding probability. The methodology for generating time series used in this paper follows the steps shown in Figure 3.

The first step is to collect data. These data are usually measured energy flows and production quantities. Data from a case study in New Zealand are used for this purpose [12]. The analysis of all essential influencing parameters of a production week requires a recording of the measured data with a suitable high temporal resolution. Seasonal effects (e.g., the weather, or availability of milk) is neglected for the heat recovery problem. If no measurement data is available (e.g., for greenfield planning), the necessary parameters could be assumed as normally distributed around average values from literature data or expert opinion.

In the second step, the time series are analyzed for possible deterministic correlations. Since the flow rate of the streams varies due to process fluctuations and discontinuous operation of the plants, which are caused by regular cleaning, maintenance work, plant failure, product change, and changing milk supply. Supply temperatures are generally quite constant, due to robust process control, and do not represent a major cause of variability in this case. Thus, the sequence of idling, production, and CIP is mandatory.

Moreover, the probabilistic components of the weekly values are described by CDF based on cumulative frequency plots. Based on the result of the statistical analysis, multiple weekly time series are generated in step three.

Due to the interaction of product changes and cleaning constraints on the energy demand, the streams have different demand profiles. Generally, two operating states can be distinguished, especially in the food industry: ”on-production”, associated with an energy demand, and “off-production” (CIP or breakdown), without any energy demand. Duration, frequency, and amplitude (i.e., production rate) of these operating conditions can be determined by statistical analysis of process time series. Constant and fluctuating energy demands can be detected. Based on that, the following three characteristic time series can be derived.

Using dairy case study data [11], the method for generating time series is demonstrated. The measurement data of two processing months are statistically evaluated to derive the weekly demand time series. Based on the load profiles in Figure 4, the frequency distributions of the heat flow rate and of the durations t for the operating states “on-production” and “off-production” are represented in the form of histograms (Figure 5a). The determinations of the frequency and cumulative probability distributions are shown in Figure 5, using the time series type (b) for stream Whey A, as an example. The computations are carried out with MATLAB® (9.3.0.713579 (R2017b), The MathWorks Inc., Natick, MA, USA).

The generation of the time series begins with the decision of whether production is “on” or “off”. The probability for this decision is calculated by the mean value from the mean duration of the “on” and “off” periods. The CDF based on the cumulative frequency plots of the heat flow rate (Figure 5b) over the production period is used to set probable heat flow rate for every time step during the operating state "on-production", by which the demand is scattered with the corresponding variance. The distributed durations of the operating states t_on for "on-production" and t_off for "off-production" can also be determined from the CDF functions (Figure 5b).

In this context, MC simulations allow the consideration of numerous probabilistic inputs to determine the distribution of probabilistic results. In line with previous studies [22,23,24] on the robustness of energy systems, probabilistic times series based on probability density functions (PDF) and CDF are used. In this way, representative data can be generated for multiple purposes, e.g., validation and sensitivity analysis.

2.3. Evaluation of the Robust Heat Recovery Loop-Dimensioning via Dynamic Monte Carlo Simulation

The stochastic time series of the heat sources and sink processes are used as input data for the thermal simulation of the HRL from Figure 1. In the sensitive simulation study, the tank size is designed for the average stream data according to the ISSP method. Furthermore, the target temperatures T_hot and T_cold of the intermediate circuits will be varied. Finally, the HRRs for different scenarios are presented depending on their probability of occurrence. The HRL (Figure 1) simulation model based on MATLAB/Simulink^® consists of heat exchangers, a stratified storage tank, and a control system. The heat exchangers are modelled according to the ε-NTU [25]. The VLH model based on the MN approach is chosen as the modelling approach for the ST [17]. The system control is divided into two parts, as shown below.

The position and width of the thermocline describe the hot and cold zone capacity and therefore serve as control criteria in the system control. The system control (Figure 6a) specifies various operating states (i.e., normal operation, loading, unloading) depending on thermocline location in the ST. If the middle of the thermocline reaches the lower or upper end of the storage tank, this is considered to be completely loaded or unloaded. The source and sink circuits are then deactivated to regenerate the stratification. For hysteresis reasons, the sources and sinks remain deactivated until the corresponding zone again occupies 10% of the storage volume. The single mass flow control (Figure 6b) adjusts the streams to the target temperatures T_hot or T_cold by mass flow control. Moreover, the growth of thermocline is contained to a certain extent $H_{t,max}$ by siphoning while the HRL and ST are still in full operation.

For evaluating the quality of the HRL system, an energetic target value for the maximum heat recovery (MHR) potential is determined according to the TAM method. The design of the HRL is carried out according to the ISSP method. Based on average stream data of a repetitive stream-wise repeat operation period (SROP) of one week, the hot and cold streams are defined. The stream data consist of average load, supply, and target temperatures. Considering a minimum temperature difference $\mathsf{\Delta }{T}_{\min }$, the hot and cold composite curves (CC) are formed. The overlapping area indicates the heat recovery potential (Figure 7a).

Depending on the form and position of the CCs, the temperatures of the intermediate circuits, as well as T_hot and T_cold, can be read directly, in addition to the number of intermediate circuits (Figure 7b). With known temperature difference (T_hot − T_cold) between the hot and the cold side of the tank and the maximum product of the difference between heat sources ${\dot{Q}}_{Sources}$ and heat sinks ${\dot{Q}}_{Sinks}$ for a certain time t, the water-based storage volume can be calculated.

$$V=\frac{\max ((\sum {\dot{Q}}_{Sources}-\sum {\dot{Q}}_{Sinks})\cdot t)}{1.16\frac{kWh}{m^3\cdot K}\cdot \left(T_{hot}-T_{cold}\right)}$$

(3)

The resulting tank size is highly dependent on the time of the occurrence of sinks and sources. Therefore, the design on the basis of one measuring profile can lead to a decrease of the HRR, or worse, to a standstill. A reliable estimation of energy savings and assessment of the tank size is only possible with a sensitivity analysis. The simulation of multiple weekly time series with random thermocline positions at the start of production evaluates the reliability and robustness of the chosen tank size. The model is also simulated applying different tank sizes. Finally, the probability distribution of the heat recovery potential for different tank sizes is evaluated based on the MC analysis.

3. Results

In the following sections, the results of the validation, the HRL sizing, and the sensitive simulation study applied to the dairy case study are presented.

3.1. Validation of the Variable Layer Height Model

The experiments described in Section 2.1 are performed for the laboratory tank, the CFD, and the VLH multi-node (MN) model. For each experiment and each model, temperature curves are compared for characteristic points over the dimensionless storage height. The degree of destratification is represented by the PIC value.

(1)

(a) Static Mode: Numerical diffusion effects are reduced to an acceptable degree, as shown in the previous study [13]. For the lab tests, the heat losses cannot be eliminated completely by the thermal insulation. For all experiments (Figure 8a–c), the thermocline grows with the simulation duration due to numerical diffusion effects. The deviation from the ideal stratification (black line) measured by the PIC values thus also increases, as shown in Figure 8d. Using the VLH model, the influence of numerical diffusion is even lower than when using the CFD model.

(b) Incoming or outgoing mass flows are still deactivated. Heat losses, on the other hand, are taken into account, which leads to the following destratification for different simulation times in Figure 9a–c. The destratification of the three models takes place to a similar extent in Figure 9d. Since no vertical heat conduction effects are taken into account for the MN approach, the stratification can only degrade evenly over the height (Figure 9b).

(2)

Establishment of the Thermocline by Charging: From a flow rate of over 1 L/min, turbulence causes destratification (Figure 10a,c). Therefore, the Courant condition has to be met, which states that a fluid particle should not move further than a node per time step. The destratification of the three models takes place to a similar extent until 1.0 L/min (Figure 10d). The degradation of the stratification of the CFD model and the lab-scale tank grows above this. On the other hand, the VLH model does not take turbulent flow forms into account, as seen in Figure 10b. For this reason, it can only be operated without restrictions up to a maximum inflow velocity of 0.002 m/s.

(3)

Operating Mode Movement: The thermocline initially moves upwards from its initial state by being filled with cold water (2 L). All models reach the expected position for the ideal behavior (black dotted lines in Figure 11a–c). After filling with warm water (4 L) the thermocline moves to the expected lower position. The storage tank is now filled to 81% with warm water. Subsequently, the predetermined heights are reached again when the tank is filled with cold water (4 L). The degradation of stratification generated by the flow rate can best be mapped by the VLH MN model (Figure 11d).

Moreover, the scalability from lab-scale sizes to industrial-scale has to be shown. Therefore, the lab-scale tank and the VLH model have the same aspect ratio (height/width) as common industrial applications. Moreover, the stratification is influenced by the flow characteristics, especially the residence time in the tank. The maximum flow velocity for the laboratory tank was 0.002 m/s, which can also be found in industrial applications. The modelled ST should be in between this range. For this reason, sufficient scalability is given.

3.2. Stochastic Time Series of Dairy Plant

For the case study, representative process data of the milk processing industry have been assembled into an exemplary complete system. This results in load profiles of the sources and sinks for a mean SROP, as seen in

Table 2. Stream table of dairy case study, producing milk powder and cream [11].

Process	Type	${\mathit{T}}_{\mathit{s}\mathit{u}\mathit{p}\mathit{p}\mathit{l}\mathit{y}}$	${\mathit{T}}_{\mathit{t}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t}}$	${\dot{\mathit{W}}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{n}\mathit{g}}$	${\dot{\mathit{H}}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{n}\mathit{g}}$	${\dot{\mathit{W}}}_{\mathit{a}\mathit{v}\mathit{e}\mathit{r}\mathit{a}\mathit{g}\mathit{e}}$	${\dot{\mathit{H}}}_{\mathit{a}\mathit{v}\mathit{e}\mathit{r}\mathit{a}\mathit{g}\mathit{e}}$
		$°\mathbf{C}$	$°\mathbf{C}$	$\mathbf{k}\mathbf{W}/\mathbf{K}$	$\mathbf{k}\mathbf{W}$	$\mathbf{k}\mathbf{W}/\mathbf{K}$	$\mathbf{k}\mathbf{W}$
Utility	Hot 1	50	30	10	195	8	160
Casein	Hot 2	50	20	49	1477	32	956
Dryer A	Hot 3	55	10	143	6415	139	6266
Dryer B	Hot 4	55	10	75	3368	73	3290
Dryer C	Hot 5	55	10	45	2020	44	1973
Milk Treatment	Cold 1	10	55	90	4057	90	4057
Whey	Cold 2	12	50	20	763	16	601
Site Hot Water	Cold 3	15	65	160	7987	160	7987

.

Using the approach for generating time series, explained in Section 2.2, various load profiles can be generated for a SROP, as presented in Figure 12 for the example of Whey A.

Profiles can be generated in the same way for all streams from Table 2. Figure 13 shows four examples of the accumulation of total sources and sink streams. This results in multiple total sink and source streams, which represent randomly arranged operating states and loads, as seen in Figure 13. These can overlap in any imaginable way.

3.3. Evaluation of the Robust Heat Recovery Loop-Dimensioning via Monte Carlo Simulation

Figure 14 shows the exemplary dimensioning of the HRL (temperature and tank size) by ISSP for the mean values. A tank volume of 1000 m³ is calculated. Since the concurrency of the sources and sinks is highly variable, the sizes 50, 100, 300, 500, and 2000 m³ are investigated by the sensitivity analysis. For all simulations, a height/diameter aspect ratio of 3/1 is chosen.

The simulation tool uses the storage temperatures, size, and loop temperatures targeted from the ISSP design. Next, the HRL is simulated for different sink and source profiles dictated by the control system. The simulation of multiple time series for each tank size with random thermocline positions at production start takes place. The distribution of the resulting HRRs for the different storage sizes and simulation runs are shown in Figure 15. The HRR is calculated by the ratio of recovered heat to the target value. For the case study with a minimum temperature difference of 5 K, a heat recovery target of 1250 MWh corresponds to the overlapping area of the hot and cold CC in Figure 14a.

Regarding the number of runs that must be carried out to achieve a distinctive probability distribution, some approaches use a convergence criterion to determine the number of simulations. In this paper, 200 simulations are run to generate probable time series, since this number shows reasonable distributions within an appropriate computing time. Storage tanks with > 1000 m³ (Figure 15f) do not achieve any further heat recovery. A high HRR can be achieved with much smaller tanks. Only the standard deviation increases significantly with decreasing size.

In total, all tank sizes in combination with the system control are suitable to achieve HHR over 90%. With decreasing storage volume at the same aspect ratio, tank height and diameter are reduced. As a result, the incoming and outgoing flow velocities temporarily rise above the limits of the validity range, which is avoided by limiting the mass flow by the control system. For this reason, the yields decrease further for smaller tank sizes.

4. Discussion

Previous studies [17] showed that a VLH MN modelling approach reduces thermocline growth, due to numerical diffusion effects while performing with suitable execution time and accuracy. The conducted validation tests confirm this and show lower thermocline growth than a CFD model. However, it should be noted that vertical heat conduction effects are not considered in the MN approach. Furthermore, the validity range of the MN approach must be restricted regarding the flow velocity, since turbulent flow effects are not taken into account. However, these operating points are to be avoided anyway for a stable HRL operation. In addition, scalability from lab-scale sizes to industrial-scale can be assumed based on the same aspect ratio (height/width).

The recording of thermal energy data for the design and evaluation of HRLs often requires a good deal of effort and is not representative of the whole operating range. One way to compensate for this is to generate one’s own time series data, also called data farming. The representativeness of the generated time series increases with the increase in basis data. Figure 5a shows a left-shifted distribution of the loads. The distributions of the durations for “on-production” and “off-production” states, on the other hand, scatter wider. If no measurement data is available, input data can be randomly distributed around expert values.

Recent study [19] had shown the relevance of risk evaluation due to the variability of streams by MC simulation methods when assessing the sensitivity of the results. The results of this study confirm this. Although the design methods provide a storage capacity of 1000 m³, the results for 50 m³ only show a HRR reduced by less than 1%. Even the insignificant further variance of the values suggests a stable operation of the HRL in combination with the existing control system over a wide operating range. A prerequisite for the extensive simulation runs is an accurate and high-performance VLH model. Based on this work, an evaluation method for robust system sizing, stable operation control, and reliable energy-saving prognosis is developed, which is applicable also to other thermal systems. Future work will investigate the robustness of heat recovery systems based on heat pumps with STs.

5. Conclusions and Outlook

The validation shows suitable accuracy and performance of the VLH model with reduced numerical diffusion effects, restricted by the validity range for non-turbulent piston flow. Furthermore, a method is developed that generates stochastic time series for a sensitivity analysis with few input values. A suitable form of sensitivity analysis is the MC simulation assessing the risk. The robustness of the HRL system is aided by the control system. The method also avoids oversizing in any of the probable operation states. The simulations show that the tank size has only a small influence on the HRR, since the mean value varies only between 95.48% and 95.90% for tank sizes of 50–2000 m³. The standard deviations are very small (< 0.54%) but increase with decreasing storage size. This leads to the conclusion that a 50 m³ tank reduces the HRR by less than 1%, with a minimally larger variance, compared to the 1000 m³ and 2000 m³ tanks. Furthermore, it is now possible to better forecast reliable energy saving.

The usage of the VLH model for a model predictive control strategy is planned for future works. In addition, an evaluation benchmark for the verification of a sufficiently large sample of time series for a convergent result should be introduced.