Evaluation of Photovoltaic and Battery Storage Effects on the Load Matching Indicators Based on Real Monitored Data
Abstract
:1. Introduction
2. Case Study and Monitored Data
2.1. Consumption Profile Analysis
2.1.1. Flats with Single Person
2.1.2. Flats with Two Persons
2.1.3. Common Space
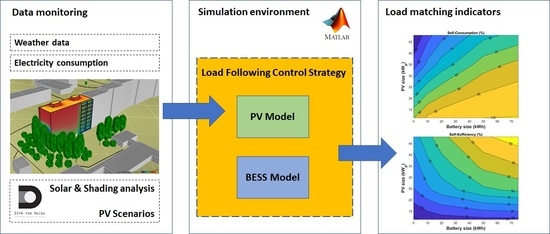
3. Methodology
3.1. Solar Potential Analysis
3.2. PV Scenarios
3.3. PV Modeling and Generation
3.4. BESS Modeling and Control Strategy
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| PV Scenario 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No BESS | BESS = 10 kWh | BESS = 20 kWh | BESS = 50 kWh | BESS = 75 kWh | ||||||
| Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | |
| 10/18 | 78.3 | 2904 | 28.6 | 2848.8 | 11.2 | 2827.3 | 0 | 2805 | 0 | 2797.4 |
| 11/18 | 1 | 3997.8 | 0 | 3993.3 | 0 | 3990.3 | 0 | 3981.2 | 0 | 3973.4 |
| 12/18 | 0.2 | 4267.2 | 0 | 4263.7 | 0 | 4260.8 | 0 | 4251.8 | 0 | 4243.2 |
| 01/19 | 2.2 | 3743.0 | 0 | 3737.5 | 0 | 3734.1 | 0 | 3724.8 | 0 | 3717.6 |
| 02/19 | 44.8 | 2647.6 | 3.8 | 2601.9 | 0 | 2594.5 | 0 | 2585 | 0 | 2577.3 |
| 03/19 | 70.2 | 3095.9 | 24.6 | 3045.0 | 7.4 | 3025.1 | 0 | 3006.1 | 0 | 1998.4 |
| 04/19 | 242.5 | 2236.4 | 95.0 | 2084.9 | 23.4 | 2002.6 | 0 | 1966.6 | 0 | 1958.9 |
| 05/19 | 238.9 | 2147.6 | 94.7 | 1998.6 | 38.6 | 1935.5 | 0 | 1881.6 | 0 | 1873.7 |
| 06/19 | 285.1 | 2040.8 | 133.9 | 1882.6 | 58.6 | 1802.4 | 0 | 1726.4 | 0 | 1718.7 |
| 07/19 | 317.2 | 1955.2 | 146.2 | 1780.4 | 58.6 | 1681.6 | 0 | 1606.6 | 0 | 1599.4 |
| 08/19 | 240.2 | 2033.3 | 78.8 | 1865.4 | 18.4 | 1795.9 | 0 | 1765.1 | 0 | 1758 |
| 09/19 | 124.9 | 2513.6 | 30.9 | 2413.7 | 4.5 | 2381.8 | 0 | 2367.2 | 0 | 2359.5 |
| PV Scenario 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No BESS | BESS = 10 kWh | BESS = 20 kWh | BESS = 50 kWh | BESS = 75 kWh | ||||||
| Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | |
| 10/18 | 220.7 | 2602.1 | 101.8 | 2478.8 | 64.5 | 2432.7 | 9 | 2364.6 | 0 | 2346.1 |
| 11/18 | 5.6 | 3836.7 | 0 | 3827.3 | 0 | 3824.4 | 0 | 3815.1 | 0 | 3807.5 |
| 12/18 | 0 | 4168.2 | 0 | 4164.7 | 0 | 4161.9 | 0 | 4152.7 | 0 | 4144.3 |
| 01/19 | 4.9 | 3583.8 | 0 | 3575.2 | 0 | 3572.1 | 0 | 3562.9 | 0 | 3555.2 |
| 02/19 | 102.1 | 2455.4 | 24.9 | 2373.4 | 6.1 | 2348.8 | 0 | 2332.9 | 0 | 2325.1 |
| 03/19 | 284.5 | 2646.8 | 141.3 | 2500.8 | 81.9 | 2431.9 | 5.3 | 2338.1 | 0 | 2325.1 |
| 04/19 | 994.6 | 1824.1 | 764.4 | 1600.4 | 579.9 | 1408.2 | 207 | 992.9 | 74 | 843.5 |
| 05/19 | 1315 | 1553.6 | 1045.6 | 1287.3 | 846.1 | 1078.7 | 404.2 | 628.3 | 263.1 | 482.7 |
| 06/19 | 1468.6 | 1438.4 | 1209.6 | 1186.1 | 1026.6 | 992.4 | 679.8 | 633.9 | 552.2 | 516 |
| 07/19 | 1524.6 | 1405 | 1246.3 | 1138.3 | 1035.5 | 914.1 | 554.3 | 419.9 | 361.8 | 223.2 |
| 08/19 | 1190.5 | 1568.6 | 933.3 | 1317.2 | 723.3 | 1096.3 | 270.5 | 611.9 | 135.1 | 468 |
| 09/19 | 552.3 | 2100.6 | 357.2 | 1902 | 233.7 | 1774.3 | 37.6 | 1548.3 | 1 | 1500.1 |
| PV Scenario 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No BESS | BESS = 10 kWh | BESS = 20 kWh | BESS = 50 kWh | BESS = 75 kWh | ||||||
| Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | |
| 10/18 | 63.1 | 2924.6 | 24.8 | 2881.5 | 8.3 | 2861.3 | 0 | 2842.7 | 0 | 2834.9 |
| 11/18 | 0 | 4027.7 | 0 | 4024.3 | 0 | 4021.4 | 0 | 4012.1 | 0 | 4004.5 |
| 12/18 | 0.2 | 4282.9 | 0 | 4279.4 | 0 | 4276.5 | 0 | 4267.5 | 0 | 4258.9 |
| 01/19 | 0.6 | 3757.6 | 0 | 3753.2 | 0 | 3750.2 | 0 | 3741.3 | 0 | 3733.3 |
| 02/19 | 31.5 | 2675.4 | 0 | 2639.3 | 0 | 2636.1 | 0 | 2626.4 | 0 | 2619.2 |
| 03/19 | 62.5 | 3080.2 | 15.8 | 3029.6 | 4 | 3012.4 | 0 | 2998.7 | 0 | 2991 |
| 04/19 | 252.1 | 2208.4 | 106.8 | 2059.8 | 33.9 | 1976.1 | 0 | 1928.4 | 0 | 1920.8 |
| 05/19 | 283.6 | 2095.4 | 131.5 | 1939.3 | 58.1 | 1857.1 | 0 | 1782.9 | 0 | 1775.2 |
| 06/19 | 355.6 | 1982.3 | 187 | 1811.5 | 95.7 | 1709.6 | 1.4 | 1595.4 | 0 | 1586 |
| 07/19 | 385.8 | 1877.1 | 200.8 | 1689.3 | 87.6 | 1564.9 | 0 | 1455.8 | 0 | 1448.9 |
| 08/19 | 285.3 | 1996.2 | 110.3 | 1820 | 27.7 | 1722.3 | 0 | 1681.7 | 0 | 1674 |
| 09/19 | 105.5 | 2515.2 | 24.8 | 2428.8 | 5.9 | 2403.8 | 0 | 2388.6 | 0 | 2381.2 |
| PV Scenario 4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No BESS | BESS = 10 kWh | BESS = 20 kWh | BESS = 50 kWh | BESS = 75 kWh | ||||||
| Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | |
| 10/18 | 717.1 | 2451.8 | 508.6 | 2252.4 | 386.8 | 2111.7 | 193.3 | 1895.1 | 117.2 | 1805.1 |
| 11/18 | 185.3 | 3622.9 | 81.7 | 3516.8 | 43.1 | 3471.9 | 2.5 | 3415.4 | 0 | 3405 |
| 12/18 | 121.4 | 3923.5 | 37.3 | 3838.2 | 3.6 | 3796.7 | 0 | 3780.8 | 0 | 3772.9 |
| 01/19 | 167.5 | 3354.7 | 85.7 | 3268.9 | 52.4 | 3233.1 | 9.9 | 3174.9 | 0 | 3155.8 |
| 02/19 | 592.9 | 2280.9 | 426.5 | 2118.5 | 323.4 | 2005.7 | 148.1 | 1804.4 | 42.3 | 1686.9 |
| 03/19 | 775.9 | 2485.4 | 574 | 2279.2 | 433.5 | 2133.7 | 197.8 | 1884 | 120.9 | 1796.4 |
| 04/19 | 1558.8 | 1754 | 1324.9 | 1531.8 | 1134.6 | 1330.2 | 654.7 | 816.7 | 480.3 | 628.5 |
| 05/19 | 1511.7 | 1532.4 | 1248.2 | 1276.5 | 1038.7 | 1056.8 | 587.3 | 592.3 | 426.4 | 428.1 |
| 06/19 | 1498.1 | 1441.5 | 1243.6 | 1188.4 | 1057.6 | 1000.2 | 704.1 | 644.8 | 587.7 | 524.4 |
| 07/19 | 1656.8 | 1405.1 | 1380 | 1137.6 | 1171.1 | 917.7 | 685.3 | 418.7 | 489.3 | 212.7 |
| 08/19 | 1623.5 | 1528.5 | 1364.4 | 1274.8 | 1154 | 1057.6 | 654.5 | 533.1 | 478.4 | 362.4 |
| 09/19 | 1194.7 | 1997.6 | 985.7 | 1791.3 | 824.9 | 1624 | 473.6 | 1263.2 | 296.4 | 1086.2 |
| PV Scenario 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No BESS | BESS = 10 kWh | BESS = 20 kWh | BESS = 50 kWh | BESS = 75 kWh | ||||||
| Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | Excess (kWh) | Grid (kWh) | |
| 10/18 | 1011.2 | 2301.5 | 782.3 | 2079.1 | 619.2 | 1907.1 | 295.1 | 1549.1 | 199.4 | 1438 |
| 11/18 | 225.7 | 3497.5 | 110.1 | 3376.4 | 62.5 | 3323.8 | 5.6 | 3251.3 | 0 | 3237 |
| 12/18 | 137.6 | 3840.5 | 46.6 | 3745.1 | 6.3 | 3701.3 | 0 | 3679.8 | 0 | 3673.2 |
| 01/19 | 205.5 | 3230.8 | 98.2 | 3121.5 | 67 | 3084.6 | 12.8 | 3014.9 | 0 | 2992 |
| 02/19 | 737.1 | 2175.6 | 546.9 | 1998.3 | 422.6 | 1854.8 | 185.8 | 1595.5 | 74.4 | 1467.6 |
| 03/19 | 1248.8 | 2295 | 997.1 | 2053.4 | 816.4 | 1863.8 | 431.5 | 1452 | 267.8 | 1290.8 |
| 04/19 | 2547 | 1577.9 | 2295.8 | 1338.2 | 2094.1 | 1133.9 | 1530.1 | 546 | 1347.7 | 367.9 |
| 05/19 | 2953 | 1303.5 | 2651.3 | 1021 | 2416.1 | 775.7 | 1818.3 | 171.8 | 1687.4 | 38.5 |
| 06/19 | 3039.5 | 1197.1 | 2761.5 | 928.3 | 2539.4 | 702.3 | 2068.8 | 243.2 | 1947.4 | 121 |
| 07/19 | 3206.3 | 1197 | 2913.2 | 915.4 | 2675.7 | 670.8 | 2134.2 | 123.6 | 2018.7 | 26.1 |
| 08/19 | 2853.7 | 1343.7 | 2563.1 | 1070.2 | 2344.3 | 838.8 | 1751.4 | 227.1 | 1596.1 | 78 |
| 09/19 | 1870.1 | 1832.4 | 1628 | 1599.9 | 1452.3 | 1416 | 980.1 | 924.4 | 749.1 | 701.9 |
References
- UNEP (United Nations Environment Programme). Building Design and Construction: Forging Resource Efficiency and Sustainable Development; UNEP: Nairobi, Kenya, 2012. [Google Scholar]
- Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the energy performance of buildings (recast). Off. J. Eur. Communities 2010, L153/13.
- IEA-PVPS Trends 2018 in photovoltaic applications. Survey Report of Selected IEA Countries between 1992 and 2017. Available online: http://www.iea-pvps.org (accessed on 20 April 2020).
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Gjorgievski, V.Z.; Chatzigeorgiou, N.G.; Venizelou, V.; Christoforidis, G.C.; Georghiou, G.E.; Papagiannis, G.K. Evaluation of Load Matching Indicators in Residential PV Systems-the Case of Cyprus. Energies 2020, 13, 1934. [Google Scholar] [CrossRef] [Green Version]
- Alrawi, O.; Bayram, I.S.; Al-Ghamdi, S.G.; Koc, M. High-Resolution Household Load Profiling and Evaluation of Rooftop PV Systems in Selected Houses in Qatar. Energies 2019, 12, 3876. [Google Scholar] [CrossRef] [Green Version]
- Aelenei, D.; Lopes, R.A.; Aelenei, L.; Gonçalves, H. Investigating the potential for energy flexibility in an office building with a vertical BIPV and a PV roof system. Renew. Energy 2019, 137, 189–197. [Google Scholar] [CrossRef] [Green Version]
- Brito, M.C.; Freitas, S.; Guimarães, S.; Catita, C.; Redweik, P. The importance of facades for the solar PV potential of a Mediterranean city using LiDAR data. Renew. Energy 2017, 111 (Suppl. C), 85–94. [Google Scholar] [CrossRef]
- Freitas, S.; Reinhart, C.; Brito, M.C. Minimizing storage needs for large scale photovoltaics in the urban environment. Sol. Energy 2018, 159, 375–389. [Google Scholar] [CrossRef]
- Mubarak, R.; Weide Luiz, E.; Seckmeyer, G. Why PV Modules Should Preferably No Longer Be Oriented to the South in the Near Future. Energies 2019, 12, 4528. [Google Scholar] [CrossRef] [Green Version]
- Skandalos, N.; Tywoniak, J. Influence of PV facade configuration on the energy demand and visual comfort in office buildings. J. Phys. Conf. Ser. 2019, 1343, 012094. [Google Scholar] [CrossRef]
- Nair, N.-K.C.; Garimella, N. Battery energy storage systems: Assessment for small-scale renewable energy integration. Energy Build. 2010, 42, 2124–2130. [Google Scholar] [CrossRef]
- Barbour, E.; Parra, D.; Awwad, Z.; González, M.C. Community energy storage: A smart choice for the smart grid? Appl. Energy 2018, 212, 489–497. [Google Scholar] [CrossRef]
- Angenendt, G.; Zurmühlen, S.; Axelsen, H.; Sauer, D.U. Comparison of different operation strategies for PV battery home storage systems including forecast-based operation strategies. Appl. Energy 2018, 229, 884–899. [Google Scholar] [CrossRef]
- Parra, D.; Patel, M.K. The nature of combining energy storage applications for residential battery technology. Appl. Energy 2019, 239, 1343–1355. [Google Scholar] [CrossRef]
- Vieira, F.M.; Moura, P.S.; de Almeida, A.T. Energy storage system for self-consumption of photovoltaic energy in residential zero energy buildings. Renew. Energy 2017, 103, 308–320. [Google Scholar] [CrossRef]
- Chatzivasileiadi, A.; Ampatzi, E.; Knight, I. Characteristics of electrical energy storage technologies and their applications in buildings. Renew. Sustain. Energy Rev. 2013, 25, 814–830. [Google Scholar] [CrossRef]
- Widén, J.; Wäckelgård, E.; Lund, P.D. Options for improving the load matching capability of distributed photovoltaics: Methodology and application to high-latitude data. Sol. Energy 2009, 83, 1953–1966. [Google Scholar] [CrossRef]
- Nyholm, E.; Goop, J.; Odenberger, M.; Johnsson, F. Solar photovoltaic-battery systems in Swedish households—Self-consumption and self-sufficiency. Appl. Energy 2016, 183, 148–159. [Google Scholar] [CrossRef] [Green Version]
- Pilz, M.; Ellabban, O.; Al-Fagih, L. On Optimal Battery Sizing for Households Participating in Demand-Side Management Schemes. Energies 2019, 12, 3419. [Google Scholar] [CrossRef] [Green Version]
- Kotarela, F.; Kyritsis, A.; Papanikolaou, N. On the Implementation of the Nearly Zero Energy Building Concept for Jointly Acting Renewables Self-Consumers in Mediterranean Climate Conditions. Energies 2020, 13, 1032. [Google Scholar] [CrossRef] [Green Version]
- Bertsch, V.; Geldermann, J.; Lühn, T. What drives the profitability of household PV investments, self-consumption and self-sufficiency? Appl. Energy 2017, 204, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Litjens, G.B.M.A.; Worrell, E.; van Sark, W.G.J.H.M. Economic benefits of combining self-consumption enhancement with frequency restoration reserves provision by photovoltaic-battery systems. Appl. Energy 2018, 223, 172–187. [Google Scholar] [CrossRef]
- Sani Hassan, A.; Cipcigan, L.; Jenkins, N. Optimal battery storage operation for PV systems with tariff incentives. Appl. Energy 2017, 203, 422–441. [Google Scholar] [CrossRef]
- Barbour, E.; González, M.C. Projecting battery adoption in the prosumer era. Appl. Energy 2018, 215, 356–370. [Google Scholar] [CrossRef] [Green Version]
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. The Economic Feasibility of Residential Energy Storage Combined with PV Panels: The Role of Subsidies in Italy. Energies 2017, 10, 1434. [Google Scholar] [CrossRef]
- Kosmadakis, I.E.; Elmasides, C.; Eleftheriou, D.; Tsagarakis, K.P. A Techno-Economic Analysis of a PV-Battery System in Greece. Energies 2019, 12, 1357. [Google Scholar] [CrossRef] [Green Version]
- Goebel, C.; Cheng, V.; Jacobsen, H.-A. Profitability of Residential Battery Energy Storage Combined with Solar Photovoltaics. Energies 2017, 10, 976. [Google Scholar] [CrossRef] [Green Version]
- Parra, D.; Norman, S.A.; Walker, G.S.; Gillott, M. Optimum community energy storage for renewable energy and demand load management. Appl. Energy 2017, 200, 358–369. [Google Scholar] [CrossRef]
- Pena-Bello, A.; Burer, M.; Patel, M.K.; Parra, D. Optimizing PV and grid charging in combined applications to improve the profitability of residential batteries. J. Energy Storage 2017, 13, 58–72. [Google Scholar] [CrossRef]
- Denholm, P.; Nunemaker, J.; Gagnon, P.; Cole, W. The potential for battery energy storage to provide peaking capacity in the United States. Renew. Energy 2020, 151, 1269–1277. [Google Scholar] [CrossRef]
- Solano, J.C.; Olivieri, L.; Caamaño-Martín, E. Assessing the potential of PV hybrid systems to cover HVAC loads in a grid-connected residential building through intelligent control. Appl. Energy 2017, 206, 249–266. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yang, H.; Li, Y. Energy storage and management system design optimization for a photovoltaic integrated low-energy building. Energy 2020, 190, 116424. [Google Scholar] [CrossRef]
- Spasic, D. Gismo Plugin. Available online: https://github.com/stgeorges/gismo/ (accessed on 15 April 2020).
- SolemmaLLC, 2019. DIVA Version 4. Available online: http://www.solemma.com/ (accessed on 15 April 2020).
- Ward, G.J. The RADIANCE lighting simulation and rendering system. In Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques; Association for Computing Machinery: New York, NY, USA, 1994; pp. 459–472. [Google Scholar]
- Daysim Software. 2013. Version 4.0. Available online: http://daysim.ning.com/ (accessed on 15 April 2020).
- Kichou, S.; Silvestre, S.; Guglielminotti, L.; Mora-López, L.; Muñoz-Cerón, E. Comparison of two PV array models for the simulation of PV systems using five different algorithms for the parameters identification. Renew. Energy 2016, 99, 270–279. [Google Scholar] [CrossRef]
- Kichou, S.; Skandalos, N.; Wolf, P. Energy performance enhancement of a research centre based on solar potential analysis and energy management. Energy 2019, 183, 1195–1210. [Google Scholar] [CrossRef]
- Bradley, T. TYPE 567: Glazed building integrated photovoltaic system. In TESS Libraries version 2.0 General Descriptions; Thermal Energy System Specialists (TESS): Madison, WI, USA, 2004. [Google Scholar]
- Skandalos, N.; Kichou, S.; Wolf, P. Energy sufficiency of an administrative building based on real data from one year of operation. In Proceedings of the 2018 Smart City Symposium Prague (SCSP), Prague, Czech Republic, 24–25 May 2018; pp. 1–8. [Google Scholar]
- Castañer, L.; Silvestre, S. Modelling Photovoltaic Systems Using PSpice®; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2002. [Google Scholar]
- Ameen, A.M.; Pasupuleti, J.; Khatib, T. Simplified performance models of photovoltaic/diesel generator/battery system considering typical control strategies. Energy Convers. Manag. 2015, 99, 313–325. [Google Scholar] [CrossRef]
- State Environmental Fund of the Czech Republic, New Green Savings Programme. Available online: https://www.sfzp.cz/en/ (accessed on 15 April 2020).












| People Count | Social Category and Activities | Appliances and Other |
|---|---|---|
|
|
|
| BESS Technology | Li-Ion NMC | PV Technology | mc-Si |
|---|---|---|---|
| Efficiency | 97% | Module area | 1.58 m2 |
| Energy | 6.3 kWh | Efficiency | 14.9 % |
| Nominal voltage | 54.7 V | Tem. Coeff. | P: −0.44%/K, Voc: −0.3%/K, Isc: 0.04 %/K |
| Nominal capacity | 116 Ah | ||
| Max. charge current | 80 A | Pmp | 245 W |
| Max. discharge current | 300 A (3 sec.) | Voc | 37.1 V |
| Self-discharge (cells) | 4%/year | Isc | 8.74 A |
| Discharge depth (DOD) | 80% | Vmp | 29.9 V |
| Full cycles | 5000 | Imp | 8.19 A |
| PV System | Suitable Surface (%) | No PV Modules | Capacity (kWp) | Performance kWh/kWp |
|---|---|---|---|---|
| Roof_1 | 22 | 47 | 11.3 | 1023.5 |
| Roof_2 | 47.6 | 102 | 24.5 | 897.2 |
| Roof_3 | 23.3 | 50 | 12 | 990.4 |
| Facade | 19.6 | 98 | 23.5 | 670.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kichou, S.; Skandalos, N.; Wolf, P. Evaluation of Photovoltaic and Battery Storage Effects on the Load Matching Indicators Based on Real Monitored Data. Energies 2020, 13, 2727. https://doi.org/10.3390/en13112727
Kichou S, Skandalos N, Wolf P. Evaluation of Photovoltaic and Battery Storage Effects on the Load Matching Indicators Based on Real Monitored Data. Energies. 2020; 13(11):2727. https://doi.org/10.3390/en13112727
Chicago/Turabian StyleKichou, Sofiane, Nikolaos Skandalos, and Petr Wolf. 2020. "Evaluation of Photovoltaic and Battery Storage Effects on the Load Matching Indicators Based on Real Monitored Data" Energies 13, no. 11: 2727. https://doi.org/10.3390/en13112727
APA StyleKichou, S., Skandalos, N., & Wolf, P. (2020). Evaluation of Photovoltaic and Battery Storage Effects on the Load Matching Indicators Based on Real Monitored Data. Energies, 13(11), 2727. https://doi.org/10.3390/en13112727