How Does the Rate of Photovoltaic Installations and Coupled Batteries Affect Regional Energy Balancing and Self-Consumption of Residential Buildings?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Environment
2.2. Description of the Study Area
2.3. Input Data
2.4. Temporal and Spatial Downscaling of the Consumption Rates
2.5. Dimensioning of the PV Systems and Batteries
3. Results
3.1. Regional Balancing and Self-Sufficiency
3.2. Self-Consumption and Energy Surplusses
3.3. Residual Loads and Regional Balancing Flows
4. Discussion
4.1. Relation Between Regional Balancing, Energy Surplusses and Self-Consumption
4.2. Applicability of the Results to Other Municipalities
4.3. Policy Implications
5. Conclusions
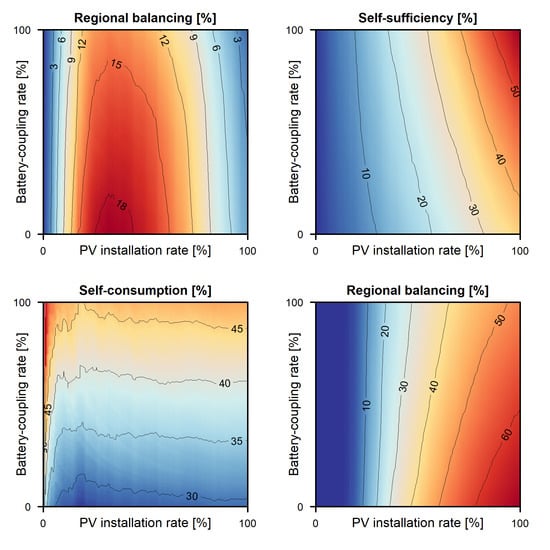
- If less than 10% of the residential buildings are equipped with PV systems, the prosumers induce minor changes of the residential residual load on regional scale under the assumption of an adequate grid infrastructure. This is also valid, if batteries are additionally utilized. State subsidies for residential PV can be fully offered without constraints.
- For PV installation rates of one third, the balancing arising from differences in the residual loads of the buildings reaches a peak value. At the maximum, 18% of the total residential consumption is produced on other buildings. The utilization of decentral battery storage systems mainly decreases this balancing effect while raising self-consumption. The magnitudes of energy excesses are not significantly reduced by the storages. Due to this, financial supporting schemes should concentrate on grid expansion and the removal of bottlenecks to enable the full energy exchange between the buildings. Incentives for residential storages do not lead to the further integration of the PV systems.
- For high degrees of buildings equipped with rooftop mounted PV systems, two third of the produced PV power cannot be consumed by the residential buildings. In this case, residential batteries can contribute to a better grid integration of residential PV by reducing low and intermediate negative residual loads. With the utilization of batteries, the residential degree of self-sufficiency reaches the maximum of 58%. The energy excesses, which cannot be consumed by the residential buildings, still account for half of the total PV production. If the residential PV expansion has already reached these high levels, state incentives should set the focus on the increased purchase of battery storage systems instead of single PV systems, as the storages help to reduce backflows into the local grids. Additional mitigation measures become mandatory for energy systems dominated by the residential sector in order to prevent power quality issues.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bruckner, T.; Bashmakov, I.A.; Mulugetta, Y.; Chum, H.; De la Vega Navarro, A.; Edmonds, J.; Faaij, A.; Fungtammasan, B.; Garg, A.; Hertwich, E.; et al. Energy Systems; Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- International Energy Agency IEA. Data and Statistics. CO2 Emissions from Electricity and Heat by Energy Source, World 1990–2018. Available online: https://www.iea.org/data-and-statistics (accessed on 19 November 2019).
- Rogelj, J.; Shindell, D.; Jiang, K.; Fifita, S.; Forster, P.; Ginzburg, V.; Handa, C.; Kheshgi, H.; Kobayashi, S.; Kriegler, E.; et al. Mitigation Pathways Compatible with 1.5 °C in the Context of Sustainable Development; Global Warming of 1.5 °C. An IPCC Special Report on the impacts of global warming of 1.5 °C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; 2018; In Press. [Google Scholar]
- Layton, B.E. A comparison of energy densities of prevalent energy sources in units of Joules per cubic meter. Int. J. Green Energy 2008, 5, 438–455. [Google Scholar] [CrossRef]
- Huber, N.; Hergert, R.; Price, B.; Zäch, C.; Hersperger, A.M.; Pütz, M.; Kienast, F.; Bolliger, J. Renewable energy sources: Conflicts and opportunities in a changing landscape. Reg. Environ. Chang. 2017, 17, 1241–1255. [Google Scholar] [CrossRef]
- Schram, W.; Louwen, A.; Lampropoulos, I.; Van Sark, W. Comparison of the greenhouse gas emission reduction potential of energy communities. Energies 2019, 12, 4440. [Google Scholar] [CrossRef] [Green Version]
- Sütterlin, B.; Siegrist, M. Public acceptance of renewable energy technologies from an abstract versus concrete perspective and the positive imagery of solar power. Energy Policy 2017, 106, 356–366. [Google Scholar] [CrossRef]
- EEG. Erneuerbare-Energien-Gesetz (Renewable Energy Sources Act) 2017; Bundesgesetzblatt I: Bonn, Germany, 2014; p. 1066. [Google Scholar]
- Gosens, J.; Kåberger, T.; Wang, Y. China’s next renewable energy revolution: Goals and mechanisms in the 13th Five Year Plan for energy. Energy Sci. Eng. 2017, 5, 141–155. [Google Scholar] [CrossRef]
- SolarPower Europe. Global Market Outlook For Solar Power 2019–2023; Solar Power Europe: Brussels, Belgium, 2019; Available online: https://www.solarpowereurope.org/wp-content/uploads/2019/07/SolarPower-Europe_Global-Market-Outlook-2019-2023.pdf (accessed on 11 November 2019).
- Bauknecht, D.; Funcke, S.; Vogel, M. Is small beautiful? A framework for assessing decentralised electricity systems. Renew. Sustain. Energy Rev. 2020, 118, 109543. [Google Scholar] [CrossRef]
- Haque, M.M.; Wolfs, P. A review of high PV penetrations in LV distribution networks: Present status, impacts and mitigation measures. Renew. Sustain. Energy Rev. 2016, 62, 1195–1208. [Google Scholar] [CrossRef]
- Figgener, J.; Haberschusz, D.; Kairies, K.P.; Wessels, O.; Tepe, B.; Sauer, D.U. Wissenschaftliches Mess- und Evaluierungsprogramm Solarstromspeicher 2.0—Jahresbericht 2018; Institut für Stromrichtertechnik und Elektrische Antriebe der RWTH Aachen: Aachen, Germany, 2018; Available online: http://www.speichermonitoring.de/fileadmin/user_upload/Speichermonitoring_Jahresbericht_2018_ISEA_RWTH_Aachen.pdf (accessed on 3 November 2019).
- Malhotra, A.; Battke, B.; Beuse, M.; Stephan, A.; Schmidt, T. Use cases for stationary battery technologies: A review of the literature and existing projects. Renew. Sustain. Energy Rev. 2016, 56, 705–721. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Moshövel, J.; Kairies, K.-P.; Magnor, D.; Leuthold, M.; Bost, M.; Gährs, S.; Szczechowicz, E.; Cramer, M.; Sauer, D.U. Analysis of the maximal possible grid relief from PV-peak-power impacts by using storage systems for increased self-consumption. Appl. Energy 2015, 137, 567–575. [Google Scholar] [CrossRef]
- Resch, M.; Ramadhani, B.; Bühler, J.; Sumper, A. Comparison of control strategies of residential PV storage systems. In Proceedings of the 9th International Renewable Energy Storage Conference and Exhibition (IRES 2015), Düsseldorf, Germany, 9–11 March 2015; pp. 1–18. [Google Scholar]
- Young, S.; Bruce, A.; MacGill, I. Potential impacts of residential PV and battery storage on Australia’s electricity networks under different tariffs. Energy Policy 2019, 128, 616–627. [Google Scholar] [CrossRef]
- Fares, R.L.; Webber, M.E. The impacts of storing solar energy in the home to reduce reliance on the utility. Nat. Energy 2017, 2, 17001. [Google Scholar] [CrossRef]
- Lee, M.; Hong, T.; Jeong, K.; Kim, J. A bottom-up approach for estimating the economic potential of the rooftop solar photovoltaic system considering the spatial and temporal diversity. Appl. Energy 2018, 232, 640–656. [Google Scholar] [CrossRef]
- Hong, T.; Lee, M.; Koo, C.; Jeong, K.; Kim, J. Development of a method for estimating the rooftop solar photovoltaic (PV) potential by analyzing the available rooftop area using hillshade analysis. Appl. Energy 2017, 194, 320–332. [Google Scholar] [CrossRef]
- Litjens, G.; Kausika, B.; Worrell, E.; van Sark, W. A spatio-temporal city-scale assessment of residential photovoltaic power integration scenarios. Sol. Energy 2018, 174, 1185–1197. [Google Scholar] [CrossRef]
- Reimuth, A.; Prasch, M.; Locherer, V.; Danner, M.; Mauser, W. Influence of different battery charging strategies on residual grid power flows and self-consumption rates at regional scale. Appl. Energy 2019, 238, 572–581. [Google Scholar] [CrossRef]
- Agnew, S.; Dargusch, P. Effect of residential solar and storage on centralized electricity supply systems. Nat. Clim. Chang. 2015, 5, 315–318. [Google Scholar] [CrossRef]
- Mauser, W.; Bach, H. PROMET—Large scale distributed hydrological modelling to study the impact of climate change on the water flows of mountain watersheds. J. Hydrol. 2009, 376, 362–377. [Google Scholar] [CrossRef]
- Mauser, W.; Bach, H.; Frank, T.; Hank, T.; Koch, F.; Marke, T.; Muerth, M.; Prasch, M.; Strasser, U.; Zabel, F. PROMET–Processes of Mass and Energy Transfer. An Integrated Land Surface Processes and Human Impacts Simulator for the Quantitative Exploration of Human-Environment Relations. Part 1: Algorithms Theoretical Baseline Document. Available online: https://www.geographie.uni-muenchen.de/department/fiona/forschung/projekte/promet_handbook/promethandbook1.pdf (accessed on 11 September 2019).
- Quaschning, V. Regenerative Energiesysteme. Technlogie—Berechnung—Simulation; Carl Hanser Verlag: München, Germany, 2013. [Google Scholar]
- Giddings, J.; LaChapelle, E. Diffusion theory applied to radiant energy distribution and albedo of snow. J. Geophys. Res. 1961, 66, 181–189. [Google Scholar] [CrossRef]
- Andrews, R.W.; Pollard, A.; Pearce, J.M. The effects of snowfall on solar photovoltaic performance. Sol. Energy 2013, 92, 84–97. [Google Scholar] [CrossRef] [Green Version]
- Locherer, V. Technical Release No. 1: INOLA Software Documentation. The Solar Energy Component. Solar Power and Solar Heat Modules; Department of Geography at LMU Munich: Munich, Germany, 2018. [Google Scholar] [CrossRef]
- Stadtwerke Unna. VDEW Lastprofile. Version October 10, 2015. Available online: http://www.gipsprojekt.de/featureGips/Gips;jsessionid=36DBE8EAF15E68329A3F6493121749DB?Session-Man-dant=sw_unna&Anwendung=EnWGKnotenAnzeigen&PrimaryId=133029&Mandantkuerzel=sw_unna&Navigation=J (accessed on 20 December 2019).
- VDEW. Repräsentative VDEW-Lastprofile; VDEW: Frankfurt, Germany, 1999; Available online: https://www.bdew.de/media/documents/1999_Repraesentative-VDEW-Lastprofile.pdf (accessed on 7 November 2019).
- Prasch, M.; Reimuth, A. Technical Release No. 5: INOLA Software Documentation. The Energy Consumption Component; Department of Geography at LMU Munich: Munich, Germany, 2018. [Google Scholar] [CrossRef]
- Reimuth, A. Technical Release No. 6: INOLA Software Documentation. The Energy Storage Component; Department of Geography at LMU Munich: Munich, Germany, 2017. [Google Scholar] [CrossRef]
- Reimuth, A. Technical Release No. 7: INOLA Software Documentation. The Energy Management Component; Department of Geography at LMU Munich: Munich, Germany, 2017. [Google Scholar] [CrossRef]
- Olaszi, B.D.; Ladanyi, J. Comparison of different discharge strategies of grid-connected residential PV systems with energy storage in perspective of optimal battery energy storage system sizing. Renew. Sustain. Energy Rev. 2017, 75, 710–718. [Google Scholar] [CrossRef]
- DWD Climate Data Center (CDC). Rasterdaten der Vieljährigen Mittleren Monatssummen und der Vieljährigen Mittleren Jahressumme für die Globalstrahlung auf die Horizontale Ebene für Deutschland basierend auf Boden- und Satellitenmessungen, Version V003. 17 August 2016. Available online: https://opendata.dwd.de/climate_environment/CDC/grids_germany/multi_annual/radiation_global/ (accessed on 5 November 2019).
- Bayerisches Landesamt für Digitalisierung, Breitband und Vermessung. Digital Terrain Model (25 m); Munich, Germany, 2015. [Google Scholar]
- Bayerisches Landesamt für Digitalisierung, Breitband und Vermessung. 3D-Building Model (LoD2); Munich, Germany, 2015. [Google Scholar]
- Bayerische Vermessungsverwaltung. Administrative Boundaries. Available online: www.geodaten.bayern.de (accessed on 11 November 2019).
- Bayerisches Landesamt für Statistik. Statistik Kommunal 2018. Stadt Bad Tölz. 09 173 112. Eine Auswahl Wichtiger Statistischer Daten. Available online: https://www.statistik.bayern.de/mam/produkte/statistik_kommunal/2018/09173112.pdf (accessed on 11 November 2019).
- Stadtwerke Bad Tölz. Feed-in data of Bad Tölz; Unpublished dataset, Stadtwerke Bad Tölz: Bad Tölz, Germany, 2019. [Google Scholar]
- DESTATIS. Material- und Energieflüsse. Stromverbrauch der Privaten Haushalte nach Haushaltsgrößenklassen. Available online: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Umwelt/Materialfluesse-Energiefluesse/Tabellen/stromverbrauch-haushalte.html (accessed on 4 November 2019).
- Arbeitsgemeinschaft der Vermessungsverwaltungen der Länder der Bundesrepublik Deutschland. ATKIS ® Basis DLM25 (AAA). 2015. Available online: https://www.ldbv.bayern.de/file/pdf/8479/basis-dlm-aaa.pdf (accessed on 11 November 2019).
- Fraunhofer, I.S.E. Recent Facts about Photovoltaics in Germany. Version of October 14, 2019; Fraunhofer ISE: Freiburg, Germany, 2019; Available online: https://www.pv-fakten.de (accessed on 11 November 2019).
- Opiyo, N. Energy storage systems for PV-based communal grids. J. Energy Storage 2016, 7, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Schoop, E. Stationäre Batterieanlagen. Auslegung, Installation und Wartung, 1st ed.; HUSS-Medien: Berlin, Germany, 2013. [Google Scholar]
- Statistische Ämter des Bundes und der Länder. Gebäude mit Wohnraum nach Baujahr (Jahrzwanzigste) und Art des Gebäudes. Auszählungsergebnis aus der Gebäude- und Wohnungszählung. Stadt Bad Tölz. Zensus Mai 2011. Available online: https://ergebnisse.zensus2011.de/#StaticContent:091730112112,GWZ_1_2_1,m,table (accessed on 5 November 2019).
- VDI. VDI Guideline 3807; Characteristic consumption values for buildings; Beuth-Verlag: Berlin, Germany, 2013. [Google Scholar]
- Bayerisches Landesamt für Statistik. Gebäude- und Wohnungsbestand: Gemeinden, Wohngebäude, Wohnungen, Wohnfläche, Stichtag. Fortschreibung des Wohngebäude- und Wohnungsbestandes. 31 December 2014. Available online: https://www.statistikdaten.bayern.de/genesis/online/ (accessed on 5 December 2019).
- Bayerisches Staatsministerium für Wirtschaft und Medien, Energie und Technologie. Bayerischer Solaratlas. Solare Energiegewinnnung; Bayerisches Staatsministerium für Wirtschaft und Medien, Energie und Technologie: Munich, Germany, 2015; Available online: https://www.stmwi.bayern.de/fileadmin/user_upload/stmwi/Publikationen/2015/2015-11-09-Bayerischer_Solaratlas.pdf (accessed on 20 December 2019).
- Bundesnetzagentur. PV Data Registrations (Excluding Ground-Mounted Installations). Data Submissions from 1 July 2017 to 31 January 2019. Available online: https://www.bundesnetzagentur.de/EN/Areas/Energy/Companies/RenewableEnergy/Facts_Figures_EEG/Register_data_tariffs/EEG_registerdata_payments_node.html (accessed on 11 November 2019).








| Parameter | Value | Source | |
|---|---|---|---|
| PV model | Efficiency module [–] | 0.173 | [45] |
| Efficiency inverter [–] | 0.98 | [45] | |
| Temperature coefficient [–] | 0.45 | [28] | |
| Constant [–] | 30.5 | [28] | |
| Ageing factor [–] | 0.001 | [45] | |
| Battery model | Nominal voltage [V] | 3.6 | [46] |
| Power energy density ratio [W/Wh] | 1 | [46] | |
| Maximum number of cycles [–] | 3000 | [46] | |
| Hourly losses [–] | 0.00000625 | [47] | |
| (Dis-) Charging Efficiency [–] | 0.99 | [46] | |
| Initial maximum depth of discharge [–] | 0.60 | [46] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reimuth, A.; Locherer, V.; Danner, M.; Mauser, W. How Does the Rate of Photovoltaic Installations and Coupled Batteries Affect Regional Energy Balancing and Self-Consumption of Residential Buildings? Energies 2020, 13, 2738. https://doi.org/10.3390/en13112738
Reimuth A, Locherer V, Danner M, Mauser W. How Does the Rate of Photovoltaic Installations and Coupled Batteries Affect Regional Energy Balancing and Self-Consumption of Residential Buildings? Energies. 2020; 13(11):2738. https://doi.org/10.3390/en13112738
Chicago/Turabian StyleReimuth, Andrea, Veronika Locherer, Martin Danner, and Wolfram Mauser. 2020. "How Does the Rate of Photovoltaic Installations and Coupled Batteries Affect Regional Energy Balancing and Self-Consumption of Residential Buildings?" Energies 13, no. 11: 2738. https://doi.org/10.3390/en13112738
APA StyleReimuth, A., Locherer, V., Danner, M., & Mauser, W. (2020). How Does the Rate of Photovoltaic Installations and Coupled Batteries Affect Regional Energy Balancing and Self-Consumption of Residential Buildings? Energies, 13(11), 2738. https://doi.org/10.3390/en13112738