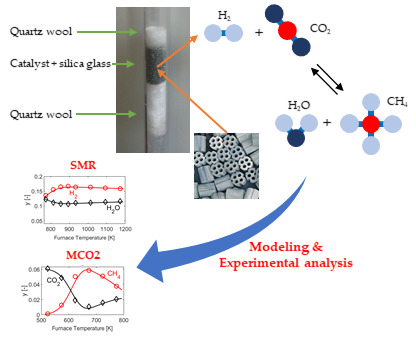
4.1. Model Calibration against Experimental Data
In
Section 3, the kinetic model was discussed in comparison to the reactor model. From a mathematical point of view, there is an essential difference between the two models. The first, i.e., the kinetic model, is an analytical non-linear equation (or a system of these). The second, i.e., the reactor model, in addition to analytical non-linear equations (the kinetic model) also includes ordinary or partial differential equations (the local mass and energy balances), requiring specific numerical integration. This is the reason why the first type of model is (more or less) easily coupled to an error minimization routine, to perform a regression of kinetic experimental data. Coupling the chemical reactor model to an error minimization routine implies a level of difficulty which is an order of magnitude higher. Thus, in this study, the procedure adopted to calibrate the model against the experimental data is a trial-and-error procedure. The experimental data are, for each catalyst, the compositions of the reacted gas stream at the sampling point, and they are reported in the subsequent Sections, in
Figure 2,
Figure 3 and
Figure 4. The absolute error between modeling and experimental molar fractions at the sampling point (
ymod and
yexp respectively), is defined as:
The percentage absolute error is defined as:
To capture the experimental data, adjusting coefficients are introduced in the kinetic subroutine, as reported in
Table 5. The kinetic parameters are kept at the original values proposed in Reference [
24]. The adjusting coefficients are tuned to minimize the percentage absolute error, averaged over all the experimental data available for each catalyst. The values of the average absolute error and average percentage absolute error are reported in
Table 6 for the three catalysts tested in this work.
The resulting values of the adjusting coefficients are reported in
Table 5. The coefficient
ζ6, related to H
2O adsorption, is 90–95 times higher for commercial catalysts than for the catalyst produced in the laboratory, and this is in line with expectations, considering the commercial catalysts have Ca and K added in order to promote H
2O adsorption. As regards the activation energies of the SMR and WGS reactions, the values of
ζ4 and
ζ5 in
Table 5 are similar to those proposed in Reference [
35], reporting values corresponding to
ζ4 = 1.07 and
ζ5 = 1.33. In addition, in Reference [
35], the activation energy of the GRR reaction is multiplied by a factor 0.97, whereas in our case, no adjusting coefficient is used (i.e., the adjusting coefficient is 1). The catalyst used in Reference [
35] was 18 wt% NiO on α-Al
2O
3 supplied by Johnson Matthey Plc, tested at about 600 °C for SMR and GRR, and at about 300 °C for WGS. Therefore, the values proposed here for the kinetic parameters agree with those reported in the literature for analogous catalysts.
4.2. HMMC Catalyst
Figure 2 reports the results obtained from the HMMC catalyst. Panels 2a–f display the results obtained in MCO2 mode, with the furnace temperature varying in the range 523–773 K. Panel 2f (red line) displays the maximum temperature in the catalytic section (PBR) of the reactor, evaluated through the simulation model. Indeed, in the catalytic section of the reactor (PBR), the exothermal revSMR reaction causes an increase of reactor temperature above that of the furnace, resulting in a mild maximum in the temperature profile, which is noticeable for a furnace temperature above 610 K. This difference between the reacting gas temperature and the furnace temperature does not exceed 40 K for any of the operating conditions considered here, and, in all cases, the simulated reactor temperature is equal to the furnace temperature at the exit of the PBR and in the subsequent P-R1, while a rapid quench down to ambient temperature occurs in P-R2, as discussed in Reference [
23].
Corresponding to panel 2f, panels 2d and 2e report the thermodynamic equilibrium constant
Kp calculated at the furnace temperature, together with the
calculated on the basis of the model results at the sampling point, respectively for the revWGS and revSMR reactions. The cited panels give a clear idea of where thermodynamic and kinetic regime are more prominent in all the experiments reported. This is an important aspect, since it has been demonstrated that the interplay between kinetics and thermodynamics has an important role in the interpretation of SMR and MCO2 experimental results [
36,
37].
According to the model, in MCO2 mode, gas compositions do not change in P-R1 and P-R2, as discussed in Reference [
23]. Thus, in
Figure 2, panels 2d and 2e demonstrate that both the revWGS and revSMR reactions are at thermodynamic equilibrium at the exit of PBR for furnace temperatures equal to or larger than T = 673 K. Conversely, the kinetic regime holds for T < 673 K. The corresponding gas compositions, measured and simulated at the sampling point (exit of P-R2), are reported in panels 2a–c. In particular, panels 2a and 2b show that, by increasing temperature, reactant (CO
2, H
2) consumption and product (CH
4, H
2O) generation increase as long as the temperature remains in the kinetic regime window. The maximum CH
4 and H
2O mol fractions (5.9% and 11.8%, respectively), and the corresponding minimum of CO
2 and H
2 (0.85% and 9.8%) are obtained around 673 K. Increasing the temperature further, the thermodynamic regime holds. Here, by increasing the temperature, the main effect is the marked decrease of the
Kp of the exothermal revSMR reaction, as shown by
Figure 2e). The simultaneous increase of the mildly endothermal revWGS (
Figure 2d) is less marked. Considering the overall revGRR reaction, its
Kp decreases strongly by increasing the temperature. Thus, by increasing the temperature, the revGRR is shifted more and more towards the reactants, and this explains the observed reduction of CH
4 and H
2O molar fractions and the associated increase of CO
2 and H
2 molar fractions displayed in panels 2a and 2b. In addition, panel 2c reports the behavior of CO, which, being produced by the revWGS and consumed by the revSMR, displays a trade-off behavior with a maximum at about 608 K, demonstrating that revWGS and revSMR kinetics prevail below and above 608 K, respectively. Above 673 K, the already discussed dominating decrease of K
p,revSMR by increasing temperature results in a continuous increase of CO.
In
Figure 2, panels 2g–r report the results obtained in SMR mode, with two different GHSVs (1.4 × 10
4 h
−1 and 2.1 × 10
4 h
−1), with furnace temperatures varying in the range 773–1173 K. The analysis is started again with a discussion of temperature results in the reactor. A temperature drop occurs close to the entrance of the packed bed (PBR), due to the endothermal SMR reaction. After the temperature drop, the temperature quickly rises and reaches the furnace temperature well before the exit of the PBR, as discussed in Reference [
23]. Here, minimum temperatures are reported in panels 2l and 2r in
Figure 2. With the HMMC catalyst, due to the high catalyst activity and the consequently fast reaction kinetics, the temperature drops are marked. Since axial heat conduction within the PBR is not considered in the model, this temperature drop may be somehow overestimated, at least for furnace temperatures above 880 K (dotted lines in panels 2l and 2r of
Figure 2). The predicted temperature occurs in a confined space. For example, for a GHSVs = 2.1 × 10
4 h
−1 and for a furnace temperature of 900 K, the minimum temperature of 765 K is reached at 0.03 mm after the entrance of the PBR, which is followed by a temperature increase up to 890 K at 1.1 mm after the entrance of the PBR.
According to the model, in SMR mode, no temperature or composition changes occur in P-R1. Conversely, a temperature decrease occurs in P-R2, in a slower fashion than in MCO2 operating mode, mainly due to the higher external temperature (523 K in SMR versus 298 K in MCO2). Simultaneously, the WGS reaction occurs in a slight, yet appreciable, way [
23]. This phenomenon of WGS occurring thermally, or catalyzed by the metallic piping, in the exit-line of experimental laboratory reactors, is reported in the literature [
33,
34,
38], and is included in the model presented in this work. These considerations make it possible to explain the results in panels 2j and 2p of
Figure 2, which, on the one hand, display that the
Kp,WGS calculated at the furnace temperature coincides with the model calculations of
at the exit of the catalytic section, showing that the model predicts WGS to be at thermodynamic equilibrium at the exit of the PBR. On the other hand, in the same figures, modeling and experimental results of
at the sampling point (exit of P-R2) are slightly higher, demonstrating a further slight advancement of the WGS reaction in P-R2.
For the SMR reaction, the experimental and simulated
at the sampling point are reported in panels 2k and 2q in
Figure 2, together with
Kp,SMR calculated at the furnace temperature. The three reported quantities coincide, demonstrating that the SMR reaction is at thermodynamic equilibrium at the exit of the reactor for all the operating conditions investigated. In particular, since no SMR reaction occurs in PR-1 or in PR-2,
Figure 2k,q demonstrate that SMR is at thermodynamic equilibrium at the exit of the packed bed (PBR), and also provide confirmation that the experimental temperature at the outlet of PBR is equal to the furnace temperature. In
Figure 2k,q, no experimental values of
are reported for temperatures above 933 K and 1013 K respectively, because the amount of methane in the sampled gaseous mixture is below the resolution of the experimental measurement system (100 ppm). Therefore, the experimental
diverges to infinity in these conditions.
The corresponding compositions measured and simulated at the sampling point, are reported in panels 2g–i of
Figure 2 for GHSV = 1.4 × 10
4 h
−1, and in panels 2m–o for GHSV = 2.1 × 10
4 h
−1. Due to SMR being endothermal, it is thermodynamically favored by increasing temperature, with a progressive increase in reactant (CH
4, H
2O) consumption and product (CO
2, H
2) generation. For furnace temperatures above 890 K, the SMR reaction is complete, with CH
4 being completely consumed inside the PBR zone of the SMR reactor. Hence, the compositions obtained by further increasing the furnace temperature are dictated by WGS. Due to WGS being mildly exothermal, it gradually shifts towards the reactants by increasing temperature, and this explains the slight decrease of CO
2 and H
2 and the associated slight increase of CO and H
2O. The maximum hydrogen molar fraction obtained experimentally is 16.7% (at a furnace temperature of 893 K for GHSV = 1.4 × 10
4 h
−1, and at a furnace temperature of 933 K for GHSV = 2.1 × 10
4 h
−1).
In SMR conditions, differences between reactor behavior at GHSV = 1.4 × 10
4 h
−1 and at GHSV = 2.1 × 10
4 h
−1 are of minor entity, and in both cases, the SMR reaction reaches thermodynamic equilibrium before the exit of the PBR, for all the operating conditions investigated. The discrepancy between experimental and simulated results reported in
Figure 2j,p, is related to the difficulty in simulating in a more accurate manner the advancement of the WGS in the exit line of the reactor.
Overall, the results offer further confirmation for the validity of the kinetic model set up by Xu and Froment [
24]. This kinetic model is typically applied to the simulation of SMR reactors [
39,
40,
41,
42]; however, since it is based on reversible reaction kinetics, it is also expected to apply to MCO2 reactors, and the results reported in panels 2a–e of
Figure 2 provide confirmation. It is interesting to notice that 773 K is the highest temperature experimented in MCO2 mode as well as the lowest temperature experimented in SMR mode. At this temperature, with the HMMC catalyst, the SMR reaction is at thermodynamic equilibrium at the exit of the PBR section of the experimental reactor, under both MCO2 and SMR operating conditions.
4.3. 57-4Q Catalyst
Figure 3 reports both modeling and experimental results obtained from the commercial 57-4Q catalyst. The first remark, when comparing the experimental results obtained in SMR and MCO2 operating modes, is that at the same temperature of 773 K, an interesting difference appears. Indeed, in MCO2 mode, the SMR reaction is at thermodynamic equilibrium at the exit of the PBR (Panel 3e), while this is clearly no longer true in SMR operating mode (Panels 3k and 3q). The possibility that this is related to thermal effects, i.e., the internal temperature of the PBR being higher than the furnace temperature in MCO2 operating mode, and lower than the furnace temperature in SMR operating mode, is considered in this work by performing a simulation of the reactor temperature profile. However, the simulated PBR temperature shows a peak/drop close to the PBR entrance, followed by an almost flat profile, very close to the furnace temperature [
23]. The entity of the peak can change from one experiment to another, but ultimately it has a rather small influence on the overall reaction rate and thus on the gas composition at the PBR exit. A more convincing explanation can be formulated considering that the literature reports that H
2O concentration strongly influences SMR kinetics [
43], and that the composition of the 57-4Q and 25-4Q catalysts improves water adsorption properties [
6]. As reported in
Table 1, both commercial catalysts are based on a calcium aluminate support, where the addition of the calcium species can result in the increase of water adsorption through neutralization of the acidic sites of alumina. Bearing in mind that the HMMC catalyst employs a calcium-free support, the different support composition may explain different water adsorption capabilities and ultimately, the strikingly different behavior observed at 773 K. This is duly reflected by the model, thanks to the water adsorption coefficient
KH2O, which, for the 57-4Q catalyst, is 90 times that of the HMMC catalyst. This makes the SMR reaction kinetics slow at high humidity levels.
The simulation results reported in
Figure 3 show satisfactory agreement with the experimental data. The highest relative error is for the calculation of the CO molar fraction at the exit of the laboratory MCO2 reactor, since the experimentally measured molar fraction is very low (
Figure 3c). In addition, the difficulty in capturing the advancement of the WGS in the exit line of the reactor in an accurate manner (
Figure 3j,p) also impacts on the accuracy of the simulation results.
In MCO2 operating mode, slight differences are found in the molar fractions at the outlet of the reactor, compared to the results obtained with the previous HMMC catalyst. This is evidenced by panels 3a–c of
Figure 3, that display a slightly reduced H
2 and CO
2 consumption, associated with a slightly reduced CH
4 and H
2O production, compared to panels 2a–c of
Figure 2. In SMR mode, the slowdown of the SMR reaction rate is visible especially in panels 3g and 3m of
Figure 3, reporting the CH
4 molar fraction at the reactor outlet. Here, CH
4 is completely converted at a furnace temperature of about 930 K, and below that temperature, the CH
4 molar fraction at the reactor outlet is visibly higher than that displayed in
Figure 2g,m, for the HMMC catalyst. Analogous considerations also apply to H
2O (panels 3h and 3n) while, for furnace temperatures below 930 K, H
2 (panels 3h and 3n) and CO
2 (panels 3g and 3m) are higher than in the in the corresponding panels in
Figure 2. For a furnace temperature higher than about 930 K, SMR thermodynamic equilibrium is established at the PBR outlet, and thus at higher temperatures, the compositions follow practically the same trend already discussed for
Figure 2.
Concerning the WGS reaction, in the Xu and Froment kinetics equations scheme [
24], the WGS kinetics is also slowed down for high
KH2O values. This slowdown of the WGS reaction results in WGS thermodynamic equilibrium not being fully established at the exit of the PBR. This is displayed by the model results reported in panels 3j and 3p of
Figure 3, in particular by the pink line not collapsing with the blue dotted line. As already discussed before, the model calculates a further advancement of the WGS reaction in the P-R2 post-reactor (green line), that is partially confirmed by the experimental data (green circles).
Concerning the simulated maximum and minimum temperatures inside the PBR, the qualitative behavior is similar to that previously discussed for the HMMC case. In more detail, in the MCO2 mode, no significant differences are observed in panel f of
Figure 2 or
Figure 3. In SMR mode, instead, differences are noticeable, since the slow SMR reaction occurring on the 57-4Q catalyst is accompanied by a small temperature drop at the entrance of the PBR, as displayed by panels 3l and r of
Figure 3. For example, for a GHSVs = 2.1 × 10
4 h
−1 and for a furnace temperature of 900 K, the reactor temperature reaches the minimum value of 870 K at 0.012 mm after the entrance of the PBR (which, according to further simulations, is followed by a temperature increase up to 890 K at 2.7 mm after the entrance of the PBR).
4.4. 25-4Q Catalyst
Figure 4 reports the results obtained from the commercial 25-4Q catalyst, which employs not only a calcium aluminate support, but also a 1.8 wt% K
2O addition, whose role is to further increase the surface basicity and avoid coke deposition [
6]. Indeed, it has been reported that, in SMR operating mode, since water adsorbs dissociatively on the catalyst surface, the increased number of sites for water adsorption increases the oxygen available on the surface, leading to an increase of the rate of carbon gasification and of the carbon monoxide production rate [
6]. Thus, in modeling the performance of the 25-4Q catalyst, the water adsorption parameter
KH2O is further increased, and is now 95 times that of the HMMC catalyst. With the 25-4Q catalyst, the increased water adsorption further slows the SMR and revSMR reaction rate, compared to the 57-4Q catalyst. This is visible by comparing panels e, k and q in
Figure 3 and
Figure 4.
Figure 4, panel 4e, shows that, in MCO2 operating mode, thermodynamic equilibrium is now reached at the PBR outlet for a furnace temperature of 773 K. Correspondingly, the maximum of CH
4 molar fraction displayed in panel 4a is now about 5%, visibly reduced compared to that reported in
Figure 3, panel 3a. Analogously, panels 4k and 4q of
Figure 4 show that, in SMR operating mode, thermodynamic equilibrium is reached for a furnace temperature of 1013 K, visibly increased compared to that displayed in
Figure 3, panels 3k and 3q. Conversely, the features of the WGS and revWGS reaction reported in
Figure 4, panels 4d, 4j and 4p, do not show appreciable variations compared to those reported in
Figure 3 panels 3d, 3j and 3p, for the 57-4Q catalyst.