On-Line Estimation of the Ultrasonic Power in a Continuous Flow Sonochemical Reactor
Abstract
:1. Introduction
2. Materials and Methods
3. Results
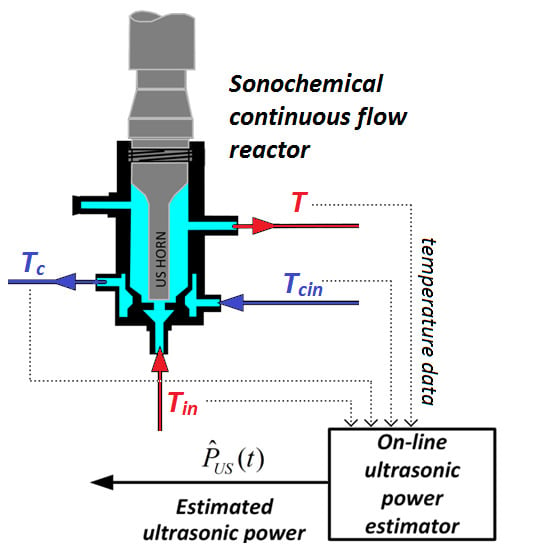
3.1. Modeling of Sonochemical Reactor
3.2. Estimation of the Ultrasonic Power
3.3. Experimental Results
4. Discussion and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Babajide, O.; Petrik, L.; Amigun, B.; Ameer, F. Low-Cost Feedstock Conversion to Biodiesel via Ultrasound Technology. Energies 2009, 3, 1691–1703. [Google Scholar] [CrossRef] [Green Version]
- Panda, D.; Manickam, S. Cavitation Technology—The Future of Greener Extraction Method: A Review of the Extraction of Natural Products and Process Intensification Mechanism and Perspectives. Appl. Sci. 2019, 9, 766. [Google Scholar] [CrossRef] [Green Version]
- Subhedar, P.B.; Gogate, P.R. Intensification of Enzymatic Hydrolysis of Lignocellulose Using Ultrasound for Efficient Bioethanol Production: A Review. Ind. Eng. Chem. Res. 2013, 52, 11816–11828. [Google Scholar] [CrossRef]
- Kandasamy, M.; Hamawand, I.; Bowtell, L.; Seneweera, S.; Chakrabarty, S.; Yusaf, T.; Shakoor, Z.; Algayyim, S.J.M.; Eberhard, F. Investigation of Ethanol Production Potential from Lignocellulosic Material without Enzymatic Hydrolysis Using the Ultrasound Technique. Energies 2017, 10, 62. [Google Scholar] [CrossRef] [Green Version]
- Kadyirov, A.; Karaeva, J. Ultrasonic and Heat Treatment of Crude Oils. Energies 2019, 12, 3084. [Google Scholar] [CrossRef] [Green Version]
- Gondrexon, N.; Renaudin, V.; Petrier, C.; Boldo, P.; Bernis, A.; Gonthier, Y. Degradation of pentachlorophenol aqueous solutions using a continuous flow ultrasonic reactor: Experimental performance and modelling. Ultrason. Sonochem. 1999, 5, 125–131. [Google Scholar] [CrossRef]
- Bilek, S.E.; Turantaş, F. Decontamination efficiency of high power ultrasound in the fruit and vegetable industry, a review. Int. J. Food Microbiol. 2013, 166, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.-C.; Lin, H.-C.; Liu, T.-M.; Lu, J.-T.; Hung, W.-T.; Huang, Y.-R.; Tsai, Y.-C.; Kao, C.-L.; Chen, S.-Y.; Sun, C. Efficient Structure Resonance Energy Transfer from Microwaves to Confined Acoustic Vibrations in Viruses. Sci. Rep. 2016, 5, 18030. [Google Scholar] [CrossRef] [Green Version]
- Cintas, P.; Mantegna, S.; Gaudino, E.C.; Cravotto, G. A new pilot flow reactor for high-intensity ultrasound irradiation. Application to the synthesis of biodiesel. Ultrason. Sonochem. 2010, 17, 985–989. [Google Scholar] [CrossRef]
- Rong, L.; Koda, S.; Nomura, H. Study on degradation rate constant of chlorobenzene in aqueous solution using a recycle ultrasonic reactor. J. Chem. Eng. Jpn. 2001, 34, 1040–1044. [Google Scholar] [CrossRef]
- Gogate, P.R.; Sutkar, V.S.; Pandit, A.B. Sonochemical reactors: Important design and scale up considerations with a special emphasis on heterogeneous systems. Chem. Eng. J. 2011, 166, 1066–1082. [Google Scholar] [CrossRef]
- Gaudino, E.C.; Carnaroglio, D.; Boffa, L.; Cravotto, G.; Moreira, E.M.; Nunes, M.A.; Dressler, V.L.; Flores, E.M. Efficient H2O2/CH3COOH oxidative desulfurization/denitrification of liquid fuels in sonochemical flow-reactors. Ultrason. Sonochem. 2014, 21, 283–288. [Google Scholar] [CrossRef] [PubMed]
- De La Rochebrochard, S.; Suptil, J.; Blais, J.F.; Naffrechoux, E. Sonochemical efficiency dependence on liquid height and frequency in an improved sonochemical reactor. Ultrason. Sonochem. 2012, 19, 280–285. [Google Scholar] [CrossRef]
- Gogate, P.R.; Wilhelm, A.M.; Pandit, A.B. Some aspects of the design of sonochemical reactors. Ultrason. Sonochem. 2003, 10, 325–330. [Google Scholar] [CrossRef]
- Meng, Z.; Zhou, Z.; Zheng, D.; Liu, L.; Dong, J.; Yang, Y.; Li, X.; Zhang, T. Optimizing dewaterability of drinking water treatment sludge by ultrasound treatment: Correlations to sludge physicochemical properties. Ultrason. Sonochem. 2018, 45, 95–105. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nomura, M.; Matsuoka, T.; Koda, S. Effects of frequency and power of ultrasound on the size reduction of liposome. Chem. Phys. Lipids 2009, 160, 58–62. [Google Scholar] [CrossRef] [PubMed]
- Kimura, T.; Sakamoto, T.; Leveque, J.M.; Sohmiya, H.; Fujita, M.; Ikeda, S.; Ando, T. Standardization of ultrasonic power for sonochemical reaction. Ultrason. Sonochem. 1996, 3, 157–161. [Google Scholar] [CrossRef]
- Kikuchi, T.; Uchida, T. Calorimetric method for measuring high ultrasonic power using water as a heating material. J. Phys. Conf. Ser. 2011, 279, 012012. [Google Scholar] [CrossRef]
- Uchida, T.; Kikuchi, T. Effect of heat generation of ultrasound transducer on ultrasonic power measured by calorimetric method. Jpn. J. Appl. Phys. 2013, 52, 07HC01. [Google Scholar] [CrossRef]
- Dochain, D. State and parameter estimation in chemical and biochemical processes: A tutorial. J. Process Control 2013, 13, 801–818. [Google Scholar] [CrossRef]
- Abarbanel, H.D.; Creveling, D.R.; Farsian, R.; Kostuk, M. Dynamical state and parameter estimation. SIAM J. Appl. Dyn. Syst. 2009, 8, 1341–1381. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1998; pp. 109–110. [Google Scholar]
- Toson, P.; Doshi, P.; Jajcevic, D. Explicit Residence Time Distribution of a Generalised Cascade of Continuous Stirred Tank Reactors for a Description of Short Recirculation Time (Bypassing). Processes 2019, 7, 615. [Google Scholar] [CrossRef] [Green Version]
- Monnier, H.; Wilhelm, A.M.; Delmas, H. Effects of ultrasound on micromixing in flow cell. Chem. Eng. Sci. 2000, 55, 4009–4020. [Google Scholar] [CrossRef]
- Legay, M.; Simony, B.; Boldo, P.; Gondrexon, N.; Person Le, S.; Bontemps, A. Improvement of heat transfer by means of ultrasound: Application to a double-tube heat exchanger. Ultrason. Sonochem. 2012, 19, 1194–1200. [Google Scholar] [CrossRef]
- Haessig, D.A. On-line State and Parameter Estimationin Nonlinear Systems. Ph.D. Thesis, Science & Technology University, Newark, NJ, USA, May 1999. [Google Scholar]
- Narendra, K.S.; Annaswamy, A.M. Stable Adaptive Systems; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Tatjewski, P. Offset-free nonlinear Model Predictive Control with state-space process models. Arch. Control Sci. 2017, 27, 595–615. [Google Scholar] [CrossRef] [Green Version]
- Choinski, D.; Skupin, P.; Krauze, P.; Ilewicz, W.; Bielecki, Z. Isopropanol concentration control in the ultrasonic nebulization process. In Proceedings of the 22nd International Conference on Methods and Models in Automation and Robotics. MMAR 2017, Miedzyzdroje, Poland, 28–31 August 2017; pp. 31–36. [Google Scholar] [CrossRef]






| Sonication Off | Sonication On | ||||||
|---|---|---|---|---|---|---|---|
| F, mL/min | V, mL | τ, s | τ0, s | F, mL/min | V, mL | τ, s | τ0, s |
| 47 | 54 | 69 | 44 | 47 | 35 | 45 | 6.3 |
| 76 | 113 | 89 | 25 | 62 | 37 | 36 | 5.2 |
| 91 | 47 | 31 | 23 | 91 | 39 | 26 | 4.3 |
| 138 | 53 | 23 | 10 | 138 | 39 | 17 | 2.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilewicz, W.; Skupin, P.; Choiński, D.; Błotnicki, W.; Bielecki, Z. On-Line Estimation of the Ultrasonic Power in a Continuous Flow Sonochemical Reactor. Energies 2020, 13, 2952. https://doi.org/10.3390/en13112952
Ilewicz W, Skupin P, Choiński D, Błotnicki W, Bielecki Z. On-Line Estimation of the Ultrasonic Power in a Continuous Flow Sonochemical Reactor. Energies. 2020; 13(11):2952. https://doi.org/10.3390/en13112952
Chicago/Turabian StyleIlewicz, Witold, Piotr Skupin, Dariusz Choiński, Wojciech Błotnicki, and Zdzisław Bielecki. 2020. "On-Line Estimation of the Ultrasonic Power in a Continuous Flow Sonochemical Reactor" Energies 13, no. 11: 2952. https://doi.org/10.3390/en13112952
APA StyleIlewicz, W., Skupin, P., Choiński, D., Błotnicki, W., & Bielecki, Z. (2020). On-Line Estimation of the Ultrasonic Power in a Continuous Flow Sonochemical Reactor. Energies, 13(11), 2952. https://doi.org/10.3390/en13112952