1. Introduction
Two of the main global problems that we are currently facing are pollution and consumption control. In the Paris COP (United Nations Climate Change Conference 2015), the United Nations agreed to limit global warming to 1.5 degrees by 2100 and, therefore, reducing energy consumption has become a key task for achieving this goal [
1]. The fact that 27% of electricity consumption in Europe is attributed to households emphasizes the need to enact regulations promoting suitable and responsible electricity usage. In this sense, monitoring home energy consumption is an important task in order to optimize and reduce electricity usage [
2,
3]. Therefore, there will be great benefits if behavioral patterns on appliance usage could be automatically detected with an eye to modifying consumer habits [
4], with a potential reduction of 12%, depending on the type of feedback that is provided, as depicted in
Figure 1.
Thus, electricity consumption has been studied progressively more, since it has benefits for both sides: consumers and the energy companies. With regard to consumers, consumption control reduces their demand for energy [
5], as feedback in this area is proven to lead to a reduction in billing of 3% to 12% [
6,
7]. Further, disaggregation can be used to detect broken appliances [
8] and to check if appliances were left on, as proposed by Bidgely [
9], by using a smartphone application. With recent and upcoming electricity tariffs, which may change dynamically depending on current demand, users may benefit from a smart system that suggests how to delay or advance the running of certain electrical appliances. At this point, the use of smart meters has been proven to be the cheapest and most effective way to control consumption [
3].
In the case of energy providers, a disaggregated bill can be employed to provide personalized energy saving recommendations [
7,
10], grid control [
11], predictions [
12], failure detection [
13], and similar statistics.
More than 30% of home consumption is from basic appliances, like the washing machine, refrigerator, and oven. The different behaviors of these appliances make it difficult to detect their patterns based on aggregated consumption. Behavioral patterns may differ in some cases, although, in others, they are relatively close, and could be classified into four general types according to their operational states [
14], as shown in
Figure 2.
Some appliances are relatively easy to detect, as their behaviors have a characteristic pattern, as shown in
Figure 3 [
5], for the case of a refrigerator. However, not all appliances have such distinguishable patterns—ranging from kettles to washing machines—which makes their detection a difficult task, as some of their stages behave similarly. At this point, fuzzy clustering plays a role to allow for more than one clustering of classification with different degrees of belonging.
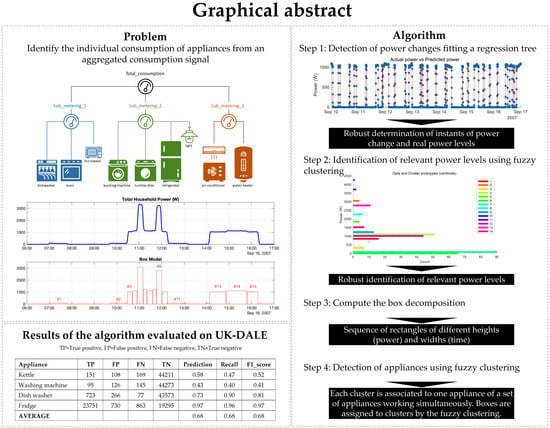
Our proposal identifies consumption patterns by detecting changes in power and building a box model to express consumption as a sequence of elastic bars with different powers and different durations. The system was built and tested using a four-year dataset with standard household consumption data collected via smart meters.
According to this, this paper is organized as follows:
Section 2 presents a review of non-intrusive load monitoring (NILM) approaches using different techniques to isolate individual patterns.
Section 3 describes the dataset used, along with the most significant fields to be analyzed.
Section 4 explains the methodology and techniques used, and
Section 5 presents the results obtained, ending with conclusions and future work.
2. State-Of-The-Art
The study of energy disaggregation is called non-intrusive load monitoring, or NILM, and was patented by George Hart in the 1980s as a basic process for showing the differences that reactive power can provide to distinguish one appliance from another [
15], as shown in
Figure 4.
Since then, many studies have emerged that have approached the problem from two perspectives:
Dealing with NILM as an optimization problem is computably unattainable because every appliance has a different set of states. We do not know the consumption of each state, and we do not know the exact number of appliances in a house that are running at the same time. And a further difficulty is that the same appliance often even produces different wave forms, as shown in
Figure 5. All these factors, added to the fact that we are handling the aggregated signals of all appliances, end up posing problems with exponential complexity, as mathematically demonstrates Kelly in Reference [
5].
In the orientation of NILM as a pattern recognition problem, there are many approaches based on event detection, meaning locating any switch in a signal from a steady state to a new state [
16,
17]. Algorithms based on event detection, once the event is detected, try to classify the most representative characteristics of a given appliance so as to differentiate and identify them [
18]. The standard procedure for this approach is represented in
Figure 6.
There are three main approaches for working with event detection in signals: expert heuristic, probabilistic models, and matched filters [
19].
Algorithms based on expert heuristic evaluations try to differentiate appliances by a set of rules with significant variables, such as power variation or power consumption. Probabilistic approaches use models to isolate the concurrence of events. They require training models to adjust variables and create statistical models, as in the case of the generalized likelihood ratio (GLR) method [
20]. To compare the heuristic method, see Reference [
21]. Yang et al. tested a probabilistic algorithm based on goodness-of-fit (GOF), with results revealing that this method’s results were more accurate and had less false positives.
The third type—matched filters—uses patterns that are correlated with the signal waveform to detect the type of appliance. In this case, a large amount of data is required [
22].
In this scope, there are many works mixing advance techniques of machine learning, and some other Artificial Intelligence algorithms, as seen in Reference [
23], since the application of advanced machine learning techniques as Hidden Markov Models [
24,
25,
26] until evolved neural networks as BP-ANNs (Back-Propagation-Artificial Neural Networks) in Reference [
27] or CNNs (Convolutional Neural Networks) in Reference [
28,
29,
30].
Our approach is framed in this third group, as it identifies sections in which several appliances can be running simultaneously. These time intervals are adaptable in length, so the problem of devices operating for different lengths of time, with the consequent weakness for pattern correlation, is solved in the proposed approach. Further, the power level identified for each box is discretized using fuzzy clustering techniques, and, consequently, the method can handle the problem of having different sets of devices with similar total power levels.
3. Description of the Dataset
Two different datasets were used in this research. The first dataset comprising electrical consumption in house in France, near Paris, collected by Georges Hebrail. This dataset is available at the Machine Learning Repository of the Center for Machine Learning and Intelligent Systems of the University of California, Irvine [
31]. It was used for the development of the proposed algorithm. A second dataset, UK-domestic appliance-level electricity (DALE) 2015 [
32], contains aggregated and disaggregated data for 5 houses located in Southern England. It was used for evaluation purposes, and it is described in the Results section.
The Paris dataset consists of a single household’s power consumption collected over the course of four years: 2007 through 2010 (precisely from 16 December 2006 17:24:00 to 26 November 2010 21:02:00). A total of 2,075,259 measurements, collected every minute, are included in the dataset. Data was collected at Sceaux (a village located south of Paris, France). This dataset was collected and made public by Georges Hebrail, Senior Researcher, EDF (Électricité de France) R&D.
This dataset contains seven variables (besides date and time), which are:
global_active_power: The total active power used at the house (kilowatts)
global_reactive_power: The total reactive power consumed by the household (kilowatts)
voltage: Average voltage (volts)
global_intensity: Average current intensity (amps)
Sub_metering_1: Active energy for kitchen (watt-hours of active energy)
Sub_metering_2: Active energy for laundry (watt-hours of active energy)
Sub_metering_3: Active energy for climate control systems (watt-hours of active energy)
Sub_metering_1 is the kitchen, primarily a dishwasher, electric oven, and a microwave oven (hot plates are not electric, but gas powered).
Sub_metering_2 is for the laundry room, containing a washing machine, a tumble dryer, refrigerator, and a light.
Sub_metering_3 is for the heating system, containing a water heater, and an air-conditioning unit.
There is some electrical equipment that is not connected to any of the three sub-meters but directly to the global meter (see
Figure 7). Therefore, the sum of Sub_metering_1, Sub_metering_2, and Sub_metering_3 (converted from watt-hours to kilowatts) does not equal to global_active_power. Nevertheless, the objective of this work is to identify different machines and detect when they are in use, so, for this purpose, we started working with the three Sub_metering signals and then demonstrated the approach for the sum of these three signals.
Some preprocessing of the data was necessary to convert energy units to power units and to smooth the values using a filter. Sub_metering data was stored in energy units (watt-hours) every minute. But it is more common to use power units, meaning the average power during the time windows, in this case one minute. Therefore, the energy values of each Sub_metering had to be multiplied by 60 to obtain the average power during every minute (in watts).
Filtering was also very convenient because the power of a small refrigerator is about 100 W, but, in energy per minute, that is only 1.67 Wh. Since the values of the smart meters used to collect the data can only be integers, the values alternate between 1 Wh and 2 Wh. Hence, a Gaussian-weighted moving average filter of size 7 was applied to the data to make it less noisy and more realistic.
4. Data Overview
The Paris dataset was previously analyzed from the time series point of view [
33], although standard data series techniques cannot detect the activation of different appliances because they do not show seasonality or fixed-time patterns. As shown in
Figure 8, the power profile of Sub_metering_2 is very predictable because it has fixed-time running/waiting cycles. This graph shows three days of data in which practically the only appliance running was the refrigerator. Only the 12th of September shows high-power activity from the washing machine, which overlaps the refrigerator’s regular activity.
Therefore, appliances, like refrigerators, are very predictable, and modeling by means of a time series model is feasible. There are some differences in the period of the signal, which may depend on the thermostat setting for the room’s temperature, although neither of them changes very often. So, a model that implements some adaptation and forgetting factors could cope with the signal type without any trouble. As an example,
Figure 9 shows the power of Sub_metering_2 in two time intervals in which no appliances were operating other than the refrigerator. The first graph corresponds to 28 June 2010—the middle of the summer—and the refrigerator starts with a period of nearly 2 h, while the second graph corresponds to 17 December 2009—winter—and the period is longer than 3 h.
Conversely, the water-heater basically starts when hot water is used in the house.
Figure 10 shows the power profile of Sub_metering_3, which includes the water heater, during the four Mondays in the month of September 2007. There is a power step reaching about 1kW every morning, which is probably triggered by using the shower. The exact time of this event is not always the same (7:05 a.m. on 3 September, 6:15 a.m. on 10 September, 7:24 a.m. on 17 September, and 6:29 a.m. on 24 September). In addition, the length of time that the water heater runs was not constant, where the variation is probably due to the amount of water used. These parameters (start time and elapsed time) depend on user behavior and cannot be predicted with time-series analysis techniques. Even when selecting the same day of the week, as in
Figure 10, which should be the most similar to each other, the power profiles are completely different.
The proposed methodology to identify which electrical appliances are installed and their usage patterns involves the use of several techniques. Firstly, regression trees [
34] are used to determine the instants of power change, as well the different consumption levels in the house. This step also lets consumption boxes with variable time lengths be detected for each power level. Secondly, clustering techniques are applied to the power levels, to minimize the effects of noisy power measurements, as well as to ascertain which power levels are actually relevant.
This approach could be implemented massively at the level of the electricity utility by using data stream models, such as the one proposed in Reference [
35].
5. Fuzzy Clustering
In an imprecise environment, like the one we have in our systems, soft computing techniques have emerged to model imprecise scenarios [
36,
37]. Clustering techniques are very popular as supervised methods that are used to classify information according to a set of properties. In NILM problems, clustering algorithms have been used to isolate patterns in several groups, combining them with other procedures to obtain better results in most cases than when using traditional clustering. In Reference [
38], Liu et al. used fuzzy clustering techniques to create a set of general models that could better detect appliances within a household. Wang et al. used fuzzy clustering, along with Hidden Markov models [
26], to retrieve single energy consumption based on the typical consumption pattern. Lin [
23,
39] proposed a hybrid system using fuzzy clustering, along with neural networks, leading to the identification of household appliances claiming an accuracy of 95%. In Reference [
40], Kamat used fuzzy logic applied to pattern recognition, in particular to detect the period of operation of a given device and thus calculate the energy consumed by that particular device.
The method that we propose is focused on the analysis of the aggregated consumption signal. In the case of several appliances operating at the same time, the consumption profiles overlap, making pattern recognition technique difficult to apply to the aggregated signal.
We use fuzzy logic and regression trees to create a box model to model changes in power and to discretize power level, allowing to differentiate devices even if the operate simultaneously. Neural methods, as Reference [
39,
41,
42], need intensive training to adjust the neural network. In our case, being an unsupervised method, we do not need large amounts of data to train our method and obtain good results, as shown in the following sections.
In our case, by segmenting electrical information, the appliances are grouped based on their “distance,” understanding this distance from a mathematical view as their closeness to each other to define two objects’ similarity. According to these groupings, we have two clustering types:
Therefore, we use an objective function to obtain the optimal number of partitions that will let us apply non-linear optimization algorithms to find a local minimum.
We have to define the number of clusters according to these three conditions, with
being the number of clusters and
the number of items:
With this scenario, we define our fuzzy space as:
Fuzzy clustering c-means is based on the optimization of fuzzy partitions [
45,
46], with
being the membership matrix
, and
being the vectors characterizing the centers of these groupings, for which we want to minimize our function.
The value of the cost function can be interpreted as a measure of the deviation between points and centers .
The minimization of this function leads to a non-linear optimization problem solved by the Picard iterative process. The restriction of membership values,
, is imposed by Lagrange multipliers.
We can demonstrate that, to minimize the function, it is necessary that:
Therefore, we need some other parameters for the algorithm, such as the number of clusters, which is one of the most relevant due to having a great impact on segmentation. The number of clusters is obtained through the fuzzy partition coefficient (FPC), which provides how well our data are explained by this grouping, that is, that membership to each one of our data segments is—in general—strong and not fuzzy. The fuzziness parameter,
, which affects fuzziness in the segmentation, is completely fuzzy if it approaches
and hard as it approaches 1. In our case, we set a value of (
, as a standard value for these types of problems, which is widely used in the bibliography. As termination criteria, we established X number of iterations and the distance matrix. This is because the calculation of distance implies establishing the scalar product matrix. The natural choice is the identity matrix (
), but a widespread distance matrix is the inverse of the covariance matrix of the data, leading to the Mahalanobis standard.
The norm used affects to the segmentation criteria, changing the measure of dissimilarity. The Mahalanobis distance leads to hyperellipsoid groupings on the axes, given by the covariances between variables.
In the bibliography, there are several modifications of this algorithm related to use an adaptative distance measure [
47,
48] and relaxing the condition on probability of belonging to each segment. According to these parameters, we checked the Euclidean norm, Mahalanobis, and Gustafson-Kessel algorithm.
The Gustafson-Kessel algorithm expanded the adaptive distance to locate different groupings with distinct geometrical forms. Each segment has its own distance provided by the equation:
The matrices
become variables that are optimized within the functional
. The only restriction is that the determinant must be positive, (
. Optimizing by using the Lagrange multipliers method, we obtain that the distance matrices must fulfill this equation:
where
is the fuzzy covariance matrix of each one of the segments.
We checked several measures to verify which ones fit the best to segment our datasets [
49].
6. Description of the Analysis Procedure
The proposed analysis approach involves several steps that are described in this section. Some of these algorithms are shown using the signal obtained by one of the smart meters, but this is just for clarification purposes, since the whole approach has been designed to be implemented on the signal measured by a single smart meter that obtains the global household power consumption. If we could expect the signals of several smart meters to be available on a regular basis in a standard household, there would be a separation of appliances that would facilitate the analysis greatly. For instance, this would make it possible, and very effective, to obtain the appliances’ typical operating patterns, such as the most-used dishwasher and washing machine cycles. Then, by applying pattern recognition techniques, it would be straightforward to detect when and how the appliances are used. However, this approach becomes very problematic when trying to analyze one global signal for the household—the sum of all the Sub_metering signals—because the power profiles of all the appliances in the house become all mixed up in the single power signal.
Nevertheless, the proposed approach identifies instants of significant power changes, power levels, and length of conditions, therefore defining a sequence of boxes of different heights and widths with which to model global power consumption. Using this box-based model, it is possible to identify which appliances are being used and when, which will enable a higher-level analysis of weekly or seasonal usage patterns. This higher-level information about usage patterns would be extremely useful for determining if small changes in schedules and habits can benefit the power network and harvest savings for the user.
6.1. Detection of Power Changes
A very simple way to detect changes in power is to work with the derivative of the power signal, although this method will be subject to many errors, due to the noise expected in the signal. Another widely-used method, and more robust, is the MATLAB function findchangepts, which is based on the algorithm described by Killick et al. [
50]. However, using this method, we found an average of 522 change points per week in the dataset of just one Sub_metering. This is much higher than expected, compared to a naked-eye detection of the signal, especially knowing that the only electrical appliance running was the hot water heater, in cycles with a fairly constant operational power level.
The proposed approach is to use regression trees [
34] to detect power changes. The tree can make a decision based on the values of the signal to determine whether or not level changes are significant to the problem. In contrast to the decision tree, created with algorithms, such as ID3, the training process of regression trees is unsupervised. Hence, it is not necessary to manually label which changes are relevant and which ones are noise. The regression tree can be automatically applied to any household without prior knowledge of the appliances installed and without any manual pre-analysis and annotation of the signals.
Trees must be pruned to avoid overfitting, to make them more generic, and to yield better overall results. The model developed in this way is very accurate and could clearly detect all 25 water-heater cycles during one week in September 2007 of data analyzing smart meter number 3, in which the air conditioning unit was not available yet.
Figure 11 shows the actual power of Sub_metering_3 in blue and the prediction of the model in red. The second graph shows the prediction error, which only has spike values during transients of power.
6.2. Power Levels
The regression tree model, described in the previous section, is able to predict the instant of power changes, along with the power level. However, the power levels in a global power signal are linear combinations of the power levels of the appliances installed in the house. Consequently, in order to generate boxes with a meaningful height, which will not be affected by signal noise, some data must be analyzed to determine what the typical power levels are in a given household.
By doing clustering analysis, we can obtain the “standard” levels of power of a given household. As depicted in
Figure 12 there are many standard levels that appear a significant number of times. The application of clustering techniques at this point helps to detect power levels without the hassle of small power changes due to the normal operation of any electrical machine.
As described in previous sections of this paper, in current applications, the use of fuzzy clustering is more suitable because the subsequent analysis of which appliance set was operating at a given time is easier if a given level can belong to several clusters and not just one. In this way, the number of clusters is reduced, and the impact of noise is even more mitigated.
6.3. Box Model
The final step in the modeling and, hence, understanding the shape of the power signal, is to produce the box model. In the proposed approach, the power signal is symbolized by a temporary sequence of rectangles of different heights and widths, which we, the authors, named the Box Model. This type of signal representation can handle the problems, described in the Data Analysis section, related to the length and temporary spacing of some cycles, such as refrigerator operation, which is different in summer and winter, or the water heater, which primarily depends on the amount of water used.
As a result of the Box Model, the first boxes of a real signal analyzed by this approach are shown in
Table 1. The values that completely define a box are the starting point in minutes, the height of the box in watts, and the width of the box in minutes. Each box represents a state of the system, and, whenever system conditions change, a new box is created.
6.4. Detection of Appliances
Each box corresponds to a state in the system, since any significant change in the power will produce a new box. These boxes are classified, based on the mean power level, applying clustering techniques. Using classic clustering, such as K-means, each box will be assigned to the closest cluster, so the appliances that are active for a given box are those represented in the cluster. The centroid of each cluster is a power level related with the electrical appliances that are in use simultaneously. One may think of the different cluster centroids as linear combinations of the operational power level of the appliances.
In contrast with classic clustering, using fuzzy clustering, one obtains, for a given box, the membership degree of that box belonging to each of cluster. Therefore, the classification of each box does not yield to a single answer, and several combinations of appliances could be considered. In general, just one of the clusters attains a high and distinctive degree, hence behaving as classic clustering. However, in some situations, the power level of the box may well represent to possible configurations of appliances. In the upcoming Results section, an example of the potential of fuzzy clustering is presented.
7. Experimental Results
In order to show the effectiveness of the Box Model proposed in this paper, all four years of data of the Paris dataset where analyzed.
Figure 13 shows the number of boxes created for every year and every month, which is an indication of the activity in the house, since each change in the consumption level creates a new box. In 2010, the graph does not include November and December because data collection runs until mid-November of that year. In 2007, the last week of July and the first 3 weeks of August there was very little activity because the house owners were probably on vacation; so, even though June through September are the hottest months of the year in Paris and Air Conditioning activity could be expected, the overall activity in 2007 is smaller. In 2008, August was the period of summer vacation and the level of activity was also smaller that in July of September.
As an example of the effectiveness of the proposed methodology for detecting the use of electrical appliances,
Figure 14 shows a challenging scenario in which several appliances are operating simultaneously, thus making the resulting total household power signal difficult to analyze. Since the dataset used for this work uses smart meters for different sections of the house, it is possible to understand the shape of the total power (subplot 4) by looking at the decomposed signals in subplots 1 through 3.
The first graph in
Figure 14 shows Sub_metering_1, which includes a consumption event that starts at 10:42 a.m. This event very likely corresponds to the dishwasher. The profile has a total duration of 80 min and is characterized by a flat power level of about 75 W, with two heating cycles 15 min long and with 2200 W of power.
The second graph shows Sub_metering_2, with very regular refrigerator cycles. This profile corresponds to an old Liebherr refrigerator that is operating every 2 h and 40 min for a period of 45 to 50 min, with a power level between 65 and 85 W. This is the most regular Sub_metering signal in the results represented in the figure.
The third graph shows Sub_metering_3, which measures the consumption of a water heater and an air conditioner. In
Figure 14, the water heater operates twice with a fairly constant power level of 1050 W. It starts for the first time at 10:30 a.m. for 1 h and 45 min and the second time starting at 2:10 p.m. with a duration of 2 h 10 min. The figure reveals that the first cycle of the water heater overlaps with the dishwasher, and the second cycle overlaps with the refrigerator, making this example interesting and challenging.
The fourth graph in
Figure 14 shows the total power, which is the sum of the three previous smart meter signals. This is the signal that was analyzed using the proposed procedure in order to create the Box Model represented in the fifth graph. The first three graphs are shown in the figure to explain the results obtained by the method.
In the resulting Box Model (fifth graph), the first couple small identical bars, as well as bar #11, are refrigerator cycles and could be easily identified by any data analysis technique. Then, there is bar #3, which is the water heater, where this profile overlaps the dishwasher in Sub_metering_1. Therefore, after 22 min at 1020 W of power, the algorithm creates a new box (bar #4) with a power level of 1110 W, representing the water heater plus the first part of dishwasher profile. Bars #5 and #9 correspond to the water heater plus high-power (heating) cycles of the dishwasher running.
Another interesting event in this graph is the second cycle of the water heater, which starts at 2:10 a.m. and overlaps with a refrigerator cycle at 2:55 p.m. The algorithm can detect the starting point (bar #13), after a small transient bar #12, which should be removed in future versions of the algorithm. Then, at 2:55 p.m., a change in power is triggered by the refrigerator cycle. The proposed method is able to detect the power change and identify a new power level of 1110 W, which was previously selected as one of the important power levels by the clustering module. Consequently, the method produces three boxes, two corresponding to the water heater alone (bar #13 and bar #15), with a power level of 1020 W, and one for the water heater and the refrigerator (bar #14), with a power level of 1110 W.
For further comparison, the algorithm was run on UK-DALE dataset, that has been widely used in the literature [
30,
41,
42,
51,
52,
53,
54,
55,
56]. Data was collected from November 2012 to May 2015, with sampling periods of 1s for aggregated and 6s for disaggregated signals. However, not all the houses cover the full range of collection time, and, in fact, there is no period of time in which data was collected from the 5 houses simultaneously. For some houses the disaggregated signals comprised several electrical appliances, so it was decided to use house 2 with 20 data channels and very fine disaggregation. The advantage of house 2 is that all appliances are well identified in separated channels of data so a ground truth for evaluation purposes can be easily generated. This dataset was preprocessed to obtain data samples every minute and selecting similar appliances as in the case of the French dataset. House 2 has interruptions in data collection at different times in different channels, so the month of July 2013 was selected as the best period of time in terms of data quality showing minimal events of missing data in 8 of the 20 channels. Signals were pre-processed to adjust the sampling period to 1 min, as in the other dataset.
Table 2 shows the average power, maximum power and total energy of each channel. Only those appliances highlighted in the table have a significant impact on the aggregated power, since other devices are less relevant for low power or marginal use. For example, small electronic devices are not interesting if operating all the time, such as the router that was only restarted 4 times in the month (was operating 99.96% of the time). The microwave is used every day but very short periods of time, mostly for less than 2 min. Finally, toaster and cooker are demanding in power, but the toaster was only used once, and the cooker was never used. A similar type of selection to focus on the relevant appliances was also done in Reference [
51,
55].
For each individual channel it is necessary to determine if the appliances were working or not, resulting in a vector of 1s and 0s that will be as the ground truth for evaluating the results. These binary vectors were obtained applying thresholds for each signal.
The dataset was evaluated using a system of 8 fuzzy clusters. A total of 2048 boxes were created automatically for the UK-DALE dataset, which is higher than in the case of the Paris dataset. It could be expected that in a more recent dataset the electrical appliances should be more efficient; nevertheless, the fridge in the UK dataset is less efficient that the refrigerator in the Paris dataset and produces more cycles. The results are typically evaluated in the literature using F1_score, which is defined as:
with Precision being the number of true positive divided by predicted positive (how many predictions are correct) and the Recall being the number of true positive divided by the condition positive (how many expected events have been correctly found).
The final results are presented on
Table 3 separated by appliances. It can be seen that Kettle and Washing Machine are harder to predict, but the fridge is detected remarkably well.
These results are consistent with previous works found in the literature. The results in Reference [
55] for houses 1, 2, and 5 together, show a slightly better overall F1_score of 0.77 in the best combination of methods, compared to 0.68. However, in Reference [
51] the results for the proposed H-ELM method are very similar: 0.67 in average F1-score, with a minimum average F1 of 0.47 for the washing machine and a maximum of 0.89 for the fridge. It is very interesting that Reference [
56] obtains the same average results of 0.63 but points out that using active and reactive power (if available) the results may improve to 0.70.
In regard to the fuzzy clustering approach presented in this paper,
Figure 15 presents the case of a Kettle event that is not correctly classified with classic clustering. In these graphs, the black dotted lines represent the centroids of the clusters associated to the dish washer (cluster #7) and to the kettle (cluster #4). Due to sampling effects, the mean power of the box in the left graph is only 2253 W high, which is lower than the typical power near 2500 W of cluster #4. As a consequence of the low power, this event would be classified as a dish washer because it is closer to cluster #7 than to cluster #4. However, with fuzzy clustering, this event was assigned a 0.496 membership degree to dish washer cluster but also a 0.432 membership degree to kettle cluster. Given that a dish washer always runs longer cycles, in this case, the system correctly selected kettle for the event. The rule that was introduced takes into account a low membership (less than 0.5 for cluster #7) and a narrow box (less than 4 min), and, in that case, the system takes the second probable cluster (cluster #4). Once this rule was introduced and run for the full dataset, the number of false positive in dish washer was reduced from 274 to 266, and the number of false negative in kettle was reduced from 175 to 169.
8. Conclusions and Future Work
Monitoring power load makes it possible to obtain usage patterns of electrical appliances, as well as real home energy consumptions. Understanding these data, small behavioral changes could be introduced that could significantly reduce costs and the environmental impact of electricity consumption. However, analyzing aggregated power consumption data is a challenging problem, especially if a previous interaction with individual electrical appliances is not possible. This field is called non-intrusive load monitoring and has been studied for years.
The work presented in this paper involves a methodology to analyze data collected with smart meters, which are currently deployed in many countries or are being installed at this time. The proposed method involves techniques for detecting changes in power based on regression trees, the selection of standard power levels of a household based on fuzzy clustering, and the creation of a Box Model to describe the aggregated power load measured by the smart meter. The system has been developed and tested using data collected in standard households by several smart meters in France and the UK. The results show that the proposed method is able to detect the usage of appliances, even in difficult situations in which several appliances overlap in time. The application of fuzzy clustering solves several cases in which classic clustering miss-classifies the events.
For future works, as fuzzy clustering allows to reduce the number of false positive and false negative, we plan to continue this analysis by the addition of new appliances.