Influence Analysis and Stepwise Regression of Coal Mechanical Parameters on Uniaxial Compressive Strength Based on Orthogonal Testing Method
Abstract
:1. Introduction
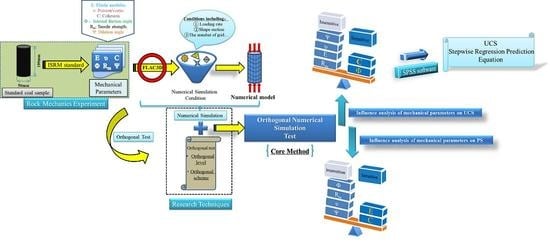
2. Orthogonal Numerical Simulation Experiments
2.1. Production of Coal Samples
2.2. Mechanical Testing and Parameter Acquisition for Coal Samples
2.2.1. Introduction of RMT-150B Servo Tester
2.2.2. Mechanical Parameter Acquisition
2.3. Numerical Simulation Test
2.3.1. Establishment of Numerical Model
2.3.2. Constitutive Model Selection
2.3.3. Model Shape Selection
2.3.4. Mesh Number of Model Element Body Is Determined
2.3.5. Loading Rate Determination
2.4. Orthogonal Experimental Method and Experimental Scheme
2.4.1. Orthogonal Experimental Method
2.4.2. Orthogonal Experimental Research Level and Scheme Design
3. Effect of Mechanical Parameters on UCS and PS
3.1. Influence Analysis of Mechanical Parameters on UCS
- (1)
- When E increases from 2.81 to 6.81 GPa, the change in UCS is minimal and the stress value fluctuates within the range 36~37 MPa. Therefore, the influence of the elastic modulus on UCS is small. According to the smaller range between axis limits, a nonlinear relationship exists between E and UCS. With increasing E, compressive strength first decreases before increasing and then decreasing again; however, the fluctuation range is small, indicating that there is a relatively stable critical range of UCS for different values of E, as shown in Figure 12a.
- (2)
- With increasing υ, UCS exhibits a fluctuating curve. In the early stage, when υ increases from 0.30 to 0.36, UCS exhibits a decrease followed by an increase and a subsequent decrease, although the maximum change range is only 0.8 MPa. Conversely, in the later stage, when υ increases from 0.36 to 0.38, the compressive strength increases from 36.08 to 37.96 MPa; this increase of 1.88 MPa is relatively pronounced. Thus, when υ is small, changes in UCS are comparatively small and UCS is not sensitive to changes in Poisson’s ratio; conversely, when υ is comparatively large, the sensitivity of UCS to changes in υ increases, as shown in Figure 12b.
- (3)
- C has a considerable influence on UCS for the coal samples, with UCS ranging from 21.94 to 50.96 MPa for different C levels. Based on curve for this specific analysis, the fitting equation between C and UCS is y = 3.628x + 0.8794, with R2 = 0.9973. There is a clear linear relationship between C and UCS, with a range of 29.02. Thus, UCS is sensitive to changes in C, increasing linearly. The results also illustrate that UCS does not converge to a critical range with variation in C, as shown in Figure 12c.
- (4)
- The influence of Φ on UCS can be divided into two stages: when Φ is less than 32°, UCS remains essentially unchanged with increasing Φ; conversely, when Φ is greater than 32°, UCS increases rapidly with increasing Φ and there is a significant linear growth relationship between the two variables. Thus, Φ has a significant impact on UCS and the degree of its influence is relatively large. Based on a comprehensive consideration of the whole curve, a nonlinear relationship exists between UCS and Φ: when Φ exceeds 32°, UCS increases linearly with increasing Φ and UCS does not have a stable critical range, as shown in Figure 12d.
- (5)
- Based on the relationship between Rm and UCS, changes in the range of UCS with increasing Rm are very small, with minimum and maximum values of 36.2 and 37.5 MPa, respectively (a range of only 1.3 MPa). Therefore, Rm has little influence on UCS. There is a significant nonlinear relationship between the two variables according to the microscopic analysis diagram, as shown in Figure 12e.
- (6)
- The relationship between Ψ and UCS indicates that, when Ψ is less than 10°, UCS first increases from 36.42 to 38.12 MPa and then decreases to 35.88 MPa with increasing Ψ (a range of 2.24 MPa). Conversely, when Ψ is greater than 10°, UCS increases from 35.88 to 36.74 MPa and then decreases to 36.46 MPa (a range of 0.86 MPa). This indicates that a nonlinear relationship exists between Ψ and UCS, with the influence of Ψ on UCS being more pronounced for small values of Ψ, as shown in Figure 12f.
3.2. Influence Analysis of Mechanical Parameters on PS
- (1)
- Based on the curve in Figure 14a, the relationship between E and PS is approximately linear. When the other parameters remain constant, PS decreases with increasing E, which is closely related to the deformation resistance of the object as characterized by E. For large values of E, the deformation resistance is greater and the deformation is less pronounced; conversely, for smaller values of E, the deformation resistance is lesser and the deformation is more pronounced.
- (2)
- PS increases slowly with increasing υ from 0.30 to 0.38; thus, the overall change in PS is small and the sensitivity of PS to υ can be considered relatively small. A smaller range between axis limits indicates that PS growth with increasing Poisson’s ratio occurs in two stages: in the first stage, υ increases from 0.3 to 0.34 and the PS growth rate is 10.13%; in the second stage, υ increases from 0.34 to 0.38 and the PS growth rate is only 2.12%. The growth rate of PS in the second stage is significantly lower than that in the first stage, although a relatively significant linear relationship exists between υ and PS in each stage, as shown in Figure 14b.
- (3)
- According to Figure 14c, PS increases linearly from 2.53 to 5.68 (range of 3.15) with increasing C. Other than E, C can be considered to have the largest influence on PS.
- (4)
- The influence of Φ on PS can also be considered to exhibit two stages. When Φ is less than 34°, the fluctuation range of PS is very small with increasing Φ and Φ thus has no effect on PS. Conversely, when Φ is greater than 34°, PS increases linearly with increasing Φ and the degree of influence of Φ on PS is greater, as shown in Figure 14d.
- (5)
- The influence of Rm on PS is variable, with no obvious regularity; the range is only 0.49 and Rm has little influence on PS. However, PS tends broadly to increase with increasing Rm, as shown in Figure 14e.
- (6)
- Based on the curve plotting PS against Ψ, PS increases from 3.91 to 4.37 as Ψ increases from 8° to 12°. This fluctuation range is small, indicating that the influence of Ψ on PS is small. Although the main plot indicates a lack of any clear linear relationship between Ψ and PS, the microscopic analysis diagram indicates that PS increases linearly with increasing Ψ before leveling off, and then exhibiting a further linear increase with Ψ at higher values of Ψ, as shown in Figure 14f.
3.3. Influence Analysis of Mechanical Parameters on Critical Failure Strength of Coal Samples
4. Stepwise Regression Prediction of UCS
4.1. Stepwise Regression Equation Analysis of Relevant Explanatory Variables and Regression Model Establishment
- (1)
- Multicollinearity means that the correlation between explanatory variables (independent variables) in the regression model is too high to be estimated or predicted by the model. If there is a linear relationship between independent variables, the reliability of the regression parameters will be affected. The VIF value, also known as the variance expansion coefficient, can be used to measure the collinear severity of a regression model. Table 8 indicates that the VIF value was 1 for both C and Φ; this is far less than the standard value of 10 required to determine the collinearity of the model. Therefore, the mechanical parameters of the orthogonal experiment were found to be independent of each other, the model did not have multiple linear problems and the model was well constructed.
- (2)
- Autocorrelation refers to correlation between the expected values of independent variables that have no significant influence on the dependent variables, which is determined by the D–W value. If the D–W value is near 2 (specifically 1.7–2.3), the model is well constructed. The D–W value of this model is 1.829 and the model construction was demonstrated to be reasonable as there was no autocorrelation among the independent variables that had no significant influence on the dependent variables.
- (3)
- The residual term represents the difference between the observed value of each sample and the value estimated by the model. In general, the normal distribution is used to test the residual term: if the test residual data conform to the normal distribution, the model can be considered to be well constructed. Residual normality is used to test the reliability and periodicity of data based on experimental sample data. The analysis of residual normality is only one of the reliability test indices to test the stepwise regression model. To judge whether the regression model conforms to the standard, only the residual items need to meet the normal distribution intuitively. The residual values of regression analysis data in this paper conform to the normal distribution, indicating that the stepwise regression model is reasonable, as shown in Figure 19.
- (4)
- The heteroscedasticity was validated by plotting scatter diagram of the independent and dependent variables with the residual term. The heteroscedasticity can be compared to the variance: it is the difference in variance between the explaining variable that omitted from the model and the unimportant explained variable. Accordingly, to determine the heteroscedasticity, the data can be examined for signs of regularity in the corresponding scattered points. If the residual is notably increased or decreased with any increase in the independent variable, the regularity is obvious; then, the model has heteroscedasticity and its construction can be considered poor. All of the independent and dependent variables considered here were plotted in a scatter diagram, as shown in Figure 20.
4.2. Reliability Analysis of Stepwise Regression Equation of Coal Compressive Strength
5. Conclusions
- (1)
- The degree of influence of mechanical parameters on UCS decreases in the following order: C > Φ > Ψ > υ > E > Rm. Thus, of these parameters, C has the greatest influence, followed by Φ. The other mechanical parameters considered have little influence on UCS for coal samples, and their relationships with UCS exhibit nonlinear characteristics. Thus, the main parameters controlling UCS are C and Φ.
- (2)
- Different mechanical parameters have different degrees of influence on PS, with degree of influence decreasing in the following order: E > C > Φ > Rm > υ > Ψ. Thus, E has the greatest influence on PS (negative linear relationship), followed by C (positive linear relationship). The other mechanical parameters considered have little influence on PS, and the main parameters controlling PS are E and C.
- (3)
- The degree of influence of mechanical parameters on peak strength has been determined based on an orthogonal simulation experiment, with the mechanical parameters without obvious significance being eliminated by a stepwise regression analysis model. The stepwise regression equation is a mathematical model with C and Φ as independent variables and UCS as a dependent variable, and the reliability of the regression prediction equation was verified. The prediction results have small error, high fitting degree and good adaptability, indicating that the model can realize the prediction of UCS.
Author Contributions
Funding
Conflicts of Interest
References
- Xie, H.P.; Peng, R.D.; Ju, Y. Energy dissipation of rock deformation and fracture. Chin. J. Rock Mech. Eng. 2004, 21, 3565–3570. [Google Scholar]
- Wu, F.B. Experimental study on mechanical characteristics of mica quartz schist foliation surface. Chin. J. Geotech. Eng. 2019, 41 (Suppl. 1), 117–120. [Google Scholar]
- Cao, W.G.; Zhang, C.; He, M.; Liu, T. Statistical damage simulation method of strain softening deformation process for rock considering characteristics of void compaction stage. Chin. J. Geotech. Eng. 2016, 10, 1754–1761. [Google Scholar]
- Matin, S.S.; Farahzadi, L.; Makaremi, S.; Chelgani, S.C.; Sattari, G. Variable selection and prediction of uniaxial compressive strength and modulus of elasticity by random forest. Appl. Soft. Comput. 2018, 70, 980–987. [Google Scholar] [CrossRef]
- Cheshomi, A.; Hajipour, G.; Hassanpour, J.; Dashtaki, B.B.; Firouzei, Y.; Sheshde, E.A. Estimation of uniaxial compressive strength of shale using indentation testing. J. Petrol. Sci. Eng. 2017, 151, 24–30. [Google Scholar] [CrossRef]
- Qin, Q.C.; Li, K.G.; Yang, B.W.; Wang, T.; Zhang, X.Y.; Guo, W. Analysis of damage characteristics of key characteristic points in the whole stress-strain process of rock. Rock Soil Mech. 2018, 39, 14–24. [Google Scholar]
- Chen, Y.L.; Zhang, Y.N.; Li, K.B.; Teng, J.Y. Distinct element numerical analysis of failure process of interlayered rock subjected to uniaxial compression. J. Min. Saf. Eng. 2017, 4, 795–802, 816. [Google Scholar]
- Lei, S.; Kang, H.P.; Gao, F.Q.; Si, L.P. Study and application of a method for rapid-determination of uniaxial compressive strength of weak coal in Xinyuan coal mine. J. China Coal Soc. 2019, 44, 3412–3422. [Google Scholar]
- Naji, A.M.; Emad, M.Z.; Rehman, H.; Yoo, H. Geological and geomechanical heterogeneity in deep hydropower tunnels: A rock burst failure case study. Tunn. Undergr. Space Technol. 2019, 84, 507–521. [Google Scholar] [CrossRef]
- Li, A.; Shao, G.J.; Su, J.B.; Liu, J.C.; Sun, Y. Uniaxial compression test and numerical simulation for alternatively soft and hard interbedded rock mass. J. Hohai Univ. (Nat. Sci.) 2018, 6, 533–538. [Google Scholar]
- Yesiloglu-Gultekin, N.; Gokceoglu, C.; Sezer, E.A. Prediction of uniaxial compressive strength of granitic rocks by various nonlinear tools and comparison of their performances. Int. J. Rock Mech. Min. 2013, 62, 113–122. [Google Scholar] [CrossRef]
- Huang, Y.G.; Zhang, T.J. Plastic failure characteristics of deep roadway with high ground stress and grouting support. J. Min. Saf. Eng. 2019, 5, 949–958. [Google Scholar]
- Si, X.F.; Gong, F.Q.; Li, X.B.; Wang, S.Y.; Luo, S. Dynamic Mohr–Coulomb and Hoek–Brown strength criteria of sandstone at high strain rates. Int. J. Rock Mech. Min. 2019, 115, 48–59. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, H.B.; Jiang, B.; Gao, S.; Li, S.C.; Gao, H.K. The method of predicting rock uniaxial compressive strength based on digital drilling and support vector machine. Rock Soil Mech. 2019, 40, 1221–1228. [Google Scholar]
- Yang, X.; Meng, Y.F.; Li, G.; Wang, L.; Li, C. An empirical equation to estimate uniaxial compressive strength for anisotropic rocks. Rock Soil Mech. 2017, 9, 2611–2655. [Google Scholar]
- Li, Y.W.; Jiang, Y.D.; Yang, Y.M.; Zhang, K.X.; Ren, Z.; Li, H.T.; Ma, Z.Q. Research on loading rate effect ofuniaxial compressive strength of coal. J. Min. Saf. Eng. 2016, 4, 754–760. [Google Scholar]
- Chen, P.; Liu, C.Y.; Wang, Y.Y. Size effect on peak axial strain and stress-strain behavior of concrete subjected to axial compression. Constr. Build. Mater. 2018, 10, 645–655. [Google Scholar] [CrossRef]
- Lu, G.D.; Yan, E.C.; Wang, H.L.; Wang, X.M.; Xie, L.F. Prediction on uniaxial compressive strength of carbonate based on geological nature of rock. J. Jilin Uni. (Earth. Sci. Ed) 2013, 6, 1915–1921+1935. [Google Scholar]
- Palchik, V. Use of stress–strain model based on Haldane’s distribution function for prediction of elastic modulus. Int. J. Rock Mech. Min. 2007, 4, 514–524. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, Y.S.; Xiao, H.B.; Zhang, C.Q.; Fu, Y.P. Research on loading rate effect on tensile strength property on hard brittle marble-teat characteristics and mechanism. Chin. J. Rock Mech. Eng. 2013, 9, 1868–1875. [Google Scholar]
- He, P.; Liu, C.W.; Wang, C.; You, S.; Wang, W.Q.; Li, L. Correlation analysis of uniaxial compressive strength and elastic modulus of sedimentary. J. Sichuan Univ. (Eng. Sci. Ed.) 2011, 4, 7–12. [Google Scholar]
- Yang, K.; Yuan, L.; Qi, L.G.; Liao, B.C. Establishing predictive model for rock uniaxial compressive strengthon No.11-2 coal seam roof in Huainan mining area. Chin. J. Rock Mech. Eng. 2013, 10, 1991–1998. [Google Scholar]
- Ashtari, M.; Mousavi, S.E.; Cheshomi, A.; Khamechian, M. Evaluation of the single compressive strength test in estimating uniaxial compressive and Brazilian tensile strengths and elastic modulus of marlstone. Eng. Geol. 2019, 248, 256–266. [Google Scholar] [CrossRef]
- Qi, L.G.; Yang, K.; Lu, W.; Yan, S.Y. Statistical Analysis on Uniaxial Compressive Strength of Coal Measures. Coal Sci. Technol. 2013, 2, 100–103. [Google Scholar]
- Lin, B.; Xu, D. Relationship between uniaxial compressive strength and elastic modulus of rocks based on different lithological characters. Saf. Coal Mines 2017, 3, 160–162, 166. [Google Scholar]
- Hu, Y.X.; Liu, X.R.; Xu, H.; Ge, H. Multiple linear regression prediction models to predict the uniaxial compressive strength and the elastic modulus of Pengguan complex. Geotech. Investig. Surv. 2010, 12, 15–21. [Google Scholar]
- Małkowski, P.; Ostrowski, Ł.; Brodny, J. Analysis of Young′s modulus for Carboniferous sedimentary rocks and its relationship with Uniaxial compressive strength using different methods of modulus determination. J. Sustain. Min. 2018, 3, 145–157. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Wang, S.L.; Yin, S.D.; Wu, Z.J. Strain-softening analysis of a spherical cavity. Int. J. Numer. Anal. Met. 2010, 36, 182–202. [Google Scholar] [CrossRef]
- Vermeer, P.A.; Borst, R. Non-associated plasticity for soils. Concr. Rock Heron 1984, 29, 3–64. [Google Scholar]
- Alejano, L.R.; Alonso, E. Considerations of the dilatancy angle in rocks and rock masses. Int. J. Rock Mech. Min. 2005, 42, 481–507. [Google Scholar] [CrossRef]
- Shen, H.Z.; Wang, S.L.; Liu, Q.S. Simulation of constitutive curves for strain-softening rock in triaxial compression. Rock Soil Mech. 2014, 6, 1647–1654. [Google Scholar]
- Meng, Q.B.; Han, L.J.; Qiao, W.G.; Lin, D.G.; Wei, L.C. Numerical simulation of crosssection shape optimizati-on design of deep soft rock roadway under high stress. J. Min. Saf. Eng. 2012, 5, 650–656. [Google Scholar]
- Li, G.; Liang, B.; Zhang, G.H. Deformation Features of Roadway in Highly Stressed Soft Rock and Design of Supporting Parameters. J. Min. Saf. Eng. 2009, 2, 183–186. [Google Scholar]
- Liu, J.; Zhao, G.Y.; Liang, W.Z.; Wu, H.; Peng, F.H. Numerical simulation of uniaxial compressive strength and failure characteristics in nonuniform rock materials. Rock Soil Mech. 2018, 39 (Suppl. 1), 505–512. [Google Scholar]
- Zhou, A.Z.; Lu, T.H. Elasto-plastic constitutive model of soil-structure interface in consideration of strain softening and dilation. Acta Mech. Solida Sin. 2009, 2, 171–179. [Google Scholar] [CrossRef]
- He, Z.M.; Peng, Z.B.; Cao, P.; Zhou, L.J. Test and numerical simulation for stratified rock mass under uniaxial compression. J. Cent. South Univ. (Sci. Technol.) 2010, 5, 1906–1912. [Google Scholar]
- Shen, P.W.; Tang, H.M.; Ning, Y.B.; Xia, D. A damage mechanics based on the constitutive model for strain softening rocks. Eng. Fract. Mech. 2019, 216, 106521. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. Fast Lagrangian Analysis of Continua in 3 Dimensions User’s Guide; Section 3.6, Chioce of Constitutive Model, 3-71-3-80; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2005. [Google Scholar]
- Zhou, Y.; Wang, T.; Lv, Q.; Zhu, Y.L.; Wang, X.X. Study on strain softening model of rock based on FLAC3D. J. Yangtze River Sci. Res. Inst. 2012, 5, 51–56, 61. [Google Scholar]
- Zhang, W.; Ma, Q.Y. Performance analysis on compressive strength and splitting tensile strength of the Nano-silica modified shringkage-compensating concrete under sulfate erosion. China Concrete. Cem. Prod. 2013, 12, 13–16. [Google Scholar]
- Wang, K.; Diao, X.H.; Lai, J.Y.; Huang, G.L. Engineering application comparison of strain softening model and Mohr-Columb model in FLAC3D. China Sci. 2015, 1, 55–59, 69. [Google Scholar]
- Yang, S.J.; Zeng, S.; Wang, H.L. Experimental study on mechanical effect of loading rate on limestone. Chin. J. Geotech. Eng. 2005, 7, 786–788. [Google Scholar]
- Li, W.; Tan, Z.Y. Prediction of uniaxial compressive strength of rock based on P-wave modulus. Rock Soil Mech. 2016, 37, 381–387. [Google Scholar]
- Zhao, Z.L.; Zhao, K.; Wang, X. Study on mechanical properties and damage evolution of coal-like rocks under different loading rates. Coal Sci. Technol. 2017, 10, 41–47. [Google Scholar]
- Zhao, B.C.; He, S.L.; Lu, X.X. Analysis on Influence Factors of Surface Subsidence in Shallow Coal Seam Mining. Min. Saf. Environ. Prot. 2019, 4, 104–107, 112. [Google Scholar]
- Liu, X.R.; Yang, S.Q. Numerical study of rock micromechanics parameters based on orthogonal test. J. Basic. Sci. Eng. 2018, 4, 918–928. [Google Scholar]
- Gao, F.Q.; Wang, X.K. Orthogonal numerical simulation on sensitivity of rock mechanical parameters. J. Min. Saf. Eng. 2008, 1, 95–98. [Google Scholar]
- Zhao, G.Z.; Ma, Z.G.; Zhu, Q.H.; Mao, X.B.; Feng, M.M. Roadway deformation during riding mining in soft rock. Int. J. Min. Sci. Technol. 2012, 4, 539–544. [Google Scholar] [CrossRef]
- Li, S.C.; Wang, Q.; Wang, H.T.; Jiang, B.; Wang, D.C.; Zhang, B.; Li, Y.; Ruan, Q. Model test study on surrounding rock deformation and failure mechanisms of deep roadways with thick top coal. Tunn. Undergr. Space Technol. 2015, 47, 52–63. [Google Scholar] [CrossRef]






















| Test | E (GPa) | υ | UCS (MPa) | C (MPa) | Φ (°) | Ψ (°) | Rm (MPa) |
|---|---|---|---|---|---|---|---|
| Uniaxial compression test | 3.20 | 0.35 | 20.6 | / | / | / | / |
| 2.60 | 0.22 | 18.7 | / | / | / | / | |
| 2.19 | 0.33 | 15.7 | / | / | / | / | |
| 3.22 | 0.30 | 25.4 | / | / | / | / | |
| Brazilian splitting test | / | / | / | / | / | / | 1.23 |
| / | / | / | / | / | / | 0.12 | |
| / | / | / | / | / | / | 0.81 | |
| Triaxial test | / | / | / | 10.88 | 40.5 | / | / |
| / | / | / | / | / | |||
| / | / | / | / | / | |||
| / | / | / | / | / | |||
| / | / | / | / | / | |||
| Average | 2.81 | 0.30 | 20.1 | 10.88 | 40.5 | / | |
| Adjusted parameter | 2.81 | 0.30 | 20.1 | 5.88 | 30 | 8 | 0.72 |
| C/MPa | Φ/° | η | |
|---|---|---|---|
| Cumulative plastic strain 0 | 5.88 | 30 | 0 |
| Cumulative plastic strain 0.008 | 5.76 | 28.06 | 0.0133 |
| Cumulative plastic strain 0.015 | 1.42 | 26.24 | 0.0250 |
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| E (GPa) | υ | C (MPa) | Φ (°) | Rm (MPa) | Ψ (°) | |
| 1 | 2.81 | 0.30 | 5.88 | 30 | 0.72 | 8 |
| 2 | 3.81 | 0.32 | 7.88 | 32 | 1.22 | 9 |
| 3 | 4.81 | 0.34 | 9.88 | 34 | 1.72 | 10 |
| 4 | 5.81 | 0.36 | 11.88 | 36 | 2.22 | 11 |
| 5 | 6.81 | 0.38 | 13.88 | 38 | 2.72 | 12 |
| Experimental Scheme | Mechanical Parameters | Simulation Results | ||||||
|---|---|---|---|---|---|---|---|---|
| E (GPa) | υ | C (MPa) | Φ (°) | Rm (MPa) | Ψ (°) | UCS (MPa) | PS (10−3) | |
| 1 | 2.81 | 0.30 | 5.88 | 30 | 0.72 | 8 | 20.1 | 3.61 |
| 2 | 2.81 | 0.32 | 7.88 | 32 | 1.22 | 9 | 27.9 | 4.88 |
| 3 | 2.81 | 0.34 | 9.88 | 34 | 1.72 | 10 | 36.1 | 5.99 |
| 4 | 2.81 | 0.36 | 11.88 | 36 | 2.22 | 11 | 44.9 | 7.65 |
| 5 | 2.81 | 0.38 | 13.88 | 38 | 2.72 | 12 | 54.4 | 9.06 |
| 6 | 3.81 | 0.30 | 7.88 | 34 | 2.22 | 12 | 29.2 | 3.78 |
| 7 | 3.81 | 0.32 | 9.88 | 36 | 2.72 | 8 | 37.7 | 4.95 |
| 8 | 3.81 | 0.34 | 11.88 | 38 | 0.72 | 9 | 47.0 | 6.06 |
| 9 | 3.81 | 0.36 | 13.88 | 30 | 1.22 | 10 | 46.9 | 6.01 |
| 10 | 3.81 | 0.38 | 5.88 | 32 | 1.72 | 11 | 20.9 | 2.78 |
| 11 | 4.81 | 0.30 | 9.88 | 38 | 1.22 | 11 | 39.5 | 4.14 |
| 12 | 4.81 | 0.32 | 11.88 | 30 | 1.72 | 12 | 40.6 | 4.23 |
| 13 | 4.81 | 0.34 | 13.88 | 32 | 2.22 | 8 | 49.0 | 5.03 |
| 14 | 4.81 | 0.36 | 5.88 | 34 | 2.72 | 9 | 21.9 | 2.34 |
| 15 | 4.81 | 0.38 | 7.88 | 36 | 0.72 | 10 | 30.2 | 3.15 |
| 16 | 5.81 | 0.30 | 11.88 | 32 | 2.72 | 10 | 42.3 | 3.75 |
| 17 | 5.81 | 0.32 | 13.88 | 34 | 0.72 | 11 | 51.2 | 4.36 |
| 18 | 5.81 | 0.34 | 5.88 | 36 | 1.22 | 12 | 22.9 | 2.09 |
| 19 | 5.81 | 0.36 | 7.88 | 38 | 1.72 | 8 | 31.5 | 2.75 |
| 20 | 5.81 | 0.38 | 9.88 | 30 | 2.22 | 9 | 40.5 | 3.47 |
| 21 | 6.81 | 0.30 | 13.88 | 36 | 1.72 | 9 | 53.3 | 3.95 |
| 22 | 6.81 | 0.32 | 5.88 | 38 | 2.22 | 10 | 23.9 | 1.85 |
| 23 | 6.81 | 0.34 | 7.88 | 30 | 2.72 | 11 | 27.2 | 2.05 |
| 24 | 6.81 | 0.36 | 9.88 | 32 | 0.72 | 12 | 35.2 | 2.67 |
| 25 | 6.81 | 0.38 | 11.88 | 34 | 1.22 | 8 | 43.8 | 3.20 |
| UCS (MPa) | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| E (GPa) | υ | C (MPa) | Φ (°) | Rm (MPa) | Ψ (°) | |
| Average 1 | 36.68 | 36.88 | 21.94 | 35.06 | 36.74 | 36.42 |
| Average 2 | 36.34 | 36.26 | 29.20 | 35.06 | 36.20 | 38.12 |
| Average 3 | 36.24 | 36.44 | 37.80 | 36.44 | 36.48 | 35.88 |
| Average 4 | 37.68 | 36.08 | 43.72 | 37.80 | 37.50 | 36.74 |
| Average 5 | 36.68 | 37.96 | 50.96 | 39.26 | 36.70 | 36.46 |
| Range | 1.44 | 1.88 | 29.02 | 4.20 | 1.30 | 2.24 |
| PS (10−3) | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| E (GPa) | υ | C (MPa) | Φ (°) | Rm (MPa) | Ψ (°) | |
| Average 1 | 6.24 | 3.85 | 2.53 | 3.87 | 3.97 | 3.91 |
| Average 2 | 4.77 | 4.05 | 3.32 | 3.82 | 4.06 | 4.14 |
| Average 3 | 3.78 | 4.24 | 4.24 | 3.93 | 3.94 | 4.15 |
| Average 4 | 3.28 | 4.28 | 4.98 | 4.36 | 4.36 | 4.20 |
| Average 5 | 2.74 | 4.33 | 5.68 | 4.78 | 4.43 | 4.37 |
| Range | 3.50 | 0.48 | 3.15 | 0.96 | 0.49 | 0.46 |
| E | υ | C | Φ | Rm | Ψ | |
|---|---|---|---|---|---|---|
| Range (UCS) | 1.44 | 1.88 | 29.02 | 4.20 | 1.30 | 2.24 |
| Range (PS) | 3.50 | 0.48 | 3.15 | 0.96 | 0.49 | 0.46 |
| Range normalization (UCS) | 0.036 | 0.047 | 0.724 | 0.105 | 0.032 | 0.056 |
| Range normalization (PS) | 0.387 | 0.053 | 0.349 | 0.106 | 0.054 | 0.051 |
| Non-Standardized Coefficient | Standardization Coefficient | t | p | VIF | R2 | Adjusted R2 | F | ||
|---|---|---|---|---|---|---|---|---|---|
| B | Standard Error | Beta | |||||||
| Constant | −18.059 | 3.704 | - | −4.876 | 0.000 ** | - | 0.983 | 0.981 | 619.574 (0.000 **) |
| C | 3.628 | 0.104 | 0.980 | 34.79 | 0.000 ** | 1.000 | |||
| Φ | 0.557 | 0.104 | 0.150 | 5.342 | 0.000 ** | 1.000 | |||
| Coal Sample | E (GPa) | C (MPa) | Φ (°) | UCS (MPa) | Stepwise Regression | Quadratic Regression | ||
|---|---|---|---|---|---|---|---|---|
| Predicted Value | Error | Predicted Value | Error | |||||
| ZL3 coal seam | 4.32 | 6.4 | 25.2 | 22.36 | 19.2 | 14.13% | 29.09 | 30.1% |
| BD3 down coal seam | 13.93 | 8.2 | 30.24 | 26.63 | 28.53 | 7.15% | 66.38 | 149.36% |
| BD 3 coal seam | 14.35 | 7.0 | 30 | 25.91 | 24.05 | 7.19% | 67.94 | 162.20% |
| HH 3 coal seam | 7.87 | 5.4 | 32.3 | 18.22 | 19.67 | 7.15% | 43.23 | 137.28% |
| XH 3 coal seam | 5.23 | 5.7 | 29.3 | 19.22 | 18.94 | 1.45% | 32.76 | 70.44% |
| DT3 coal seam | 3.97 | 5.64 | 31.5 | 19.6 | 19.95 | 1.78% | 27.68 | 41.21% |
| DT 3 up coal seam | 3.43 | 5.52 | 33 | 20.82 | 20.35 | 2.26% | 25.48 | 22.39% |
| DT 3 down coal seam | 3.8 | 6.5 | 33 | 24.04 | 23.9 | 0.57% | 26.99 | 12.26% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Wang, J.; Jiang, L.; Zhou, T.; Yan, X.; Yuan, L.; Chen, W. Influence Analysis and Stepwise Regression of Coal Mechanical Parameters on Uniaxial Compressive Strength Based on Orthogonal Testing Method. Energies 2020, 13, 3640. https://doi.org/10.3390/en13143640
Zhang P, Wang J, Jiang L, Zhou T, Yan X, Yuan L, Chen W. Influence Analysis and Stepwise Regression of Coal Mechanical Parameters on Uniaxial Compressive Strength Based on Orthogonal Testing Method. Energies. 2020; 13(14):3640. https://doi.org/10.3390/en13143640
Chicago/Turabian StyleZhang, Peipeng, Jianpeng Wang, Lishuai Jiang, Tao Zhou, Xianyang Yan, Long Yuan, and Wentao Chen. 2020. "Influence Analysis and Stepwise Regression of Coal Mechanical Parameters on Uniaxial Compressive Strength Based on Orthogonal Testing Method" Energies 13, no. 14: 3640. https://doi.org/10.3390/en13143640
APA StyleZhang, P., Wang, J., Jiang, L., Zhou, T., Yan, X., Yuan, L., & Chen, W. (2020). Influence Analysis and Stepwise Regression of Coal Mechanical Parameters on Uniaxial Compressive Strength Based on Orthogonal Testing Method. Energies, 13(14), 3640. https://doi.org/10.3390/en13143640