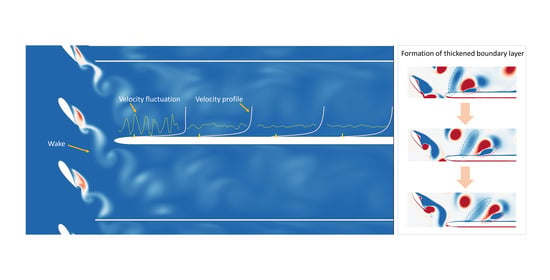
Numerical Investigation of the Turbulent Wake-Boundary Interaction in a Translational Cascade of Airfoils and Flat Plate
Abstract
:1. Introduction
2. Model and Methods
2.1. Computational Domain and Mesh Generation
2.2. Theoretical Methods
2.3. Numerical Scheme
3. Validation of the Numerical Model
4. Results and Discussions
4.1. Velocity Profiles in the Boundary Layers
4.2. Turbulence Intensity in the Boundary Layer
4.3. Convection of Wake and Wake-Induced Structure
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Courtiade, N.; Ottavy, X.; Gourdain, N. Modal decomposition for the analysis of the rotor-stator interactions in multistage compressors. J. Therm. Sci. 2012, 21, 276–285. [Google Scholar] [CrossRef]
- Vogeler, K.; Mailach, R. Rotor-Stator Interactions in a Four-Stage Low-Speed Axial Compressor-Part I: Unsteady Profile Pressures and the Effect of Clocking. J. Turbomach. 2004, 126, 833–845. [Google Scholar]
- Gourdain, N. Prediction of the Unsteady Turbulent Flow in an Axial Compressor Stage. Part 2: Analysis of Unsteady RANS and LES Data. Comput. Fluids 2015, 106, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Hetherington, R. Compressor Noise Generated by Fluctuating Lift Resulting from Rotor-Stator Interaction. AIAA J. 2012, 1, 473–474. [Google Scholar] [CrossRef]
- Dickmann, H.-P.; Wimmel, T.S.; Szwedowicz, J.; Filsinger, D.; Roduner, C.H. Unsteady Flow in a Turbocharger Centrifugal Compressor: Three-Dimensional Computational Fluid Dynamics Simulation and Numerical and Experimental Analysis of Impeller Blade Vibration. J. Turbomach. 2006, 128, 455–465. [Google Scholar] [CrossRef]
- Hodson, H.P. Boundary Layer and Loss Measurements on the Rotor of an Axial-Flow Turbine. J. Eng. Gas Turbine Power 1984, 106, 391–399. [Google Scholar] [CrossRef]
- Arndt, N.N.; Acosta, A.J.; Brennen, C.E.; Caughey, T.K. Rotor–Stator Interaction in a Diffuser Pump. J. Turbomach. 1989, 111, 213–221. [Google Scholar] [CrossRef]
- Robinson, C.; Casey, M.; Hutchinson, B.; Steed, R. Impeller-Diffuser Interaction in Centrifugal Compressors. In Proceedings of the ASME Turbo Expo, Copenhagen, Denmark, 11–15 June 2012; Volume 8. [Google Scholar] [CrossRef] [Green Version]
- Brear, M.J.; Hodson, H.P. The Effect of Wake Passing on a Flow Separation in a Low-Pressure Turbine Cascade. J. Fluids Eng. 2004, 126, 250–256. [Google Scholar] [CrossRef]
- Czarske, J.R.; Ttner, L.B.; Razik, T.; Ller, H.M. Boundary layer velocity measurements by a laser Doppler profile sensor with micrometre spatial resolution. Meas. Sci. Technol. 2002, 13, 1979–1989. [Google Scholar] [CrossRef]
- Oweis, G.F.; Winkel, E.S.; Cutbrith, J.M.; Ceccio, S.L.; Perlin, M.; Dowling, D.R. The mean velocity profile of a smooth-flat-plate turbulent boundary layer at high Reynolds number. J. Fluid Mech. 2010, 665, 357–381. [Google Scholar] [CrossRef]
- Wheeler, A.P.S.; Miller, R.J.; Hodson, H.P. The Effect of Wake Induced Structures on Compressor Boundary-Layers. J. Turbomach. 2006, 129, 705–712. [Google Scholar] [CrossRef]
- Gerolymos, G.A.; Michon, G.J.; Neubauer, J. Analysis and Application of Chorochronic Periodicity in Turbomachinery Rotor/Stator Interaction Computations. J. Propuls. Power 2002, 18, 1139–1152. [Google Scholar] [CrossRef]
- Chaluvadi, V.S.P.; Kalfas, A.I.; Banieghbal, M.R.; Hodson, H.P.; Denton, J.D. Blade-Row Interaction in a High-Pressure Turbine. J. Propuls. Power 2001, 17, 892–901. [Google Scholar] [CrossRef] [Green Version]
- Sato, W.; Yamagata, A.; Hattori, H. A Study on Unsteady Aerodynamic Excitation Forces on Radial Turbine Blade due to Rotor-Stator Interaction. In Proceedings of the 11th International Conference on Turbochargers and Turbocharging, London, UK, 13–14 May 2014; pp. 389–398. [Google Scholar]
- Kubota, Y.; Suzuki, T.; Tomita, H.; Nagafugi, T.; Okamura, C. Vibration of Rotating Bladed Disc Excited by Stationary Distributed Forces. Bull. JSME 1983, 26, 1952–1957. [Google Scholar] [CrossRef] [Green Version]
- Franke, G.; Fisher, R.; Powell, C.; Seidel, U.; Koutnik, J. On Pressure Mode Shapes Arising from Rotor-Stator Interactions. Sound Vib. 2005, 39, 14–18. [Google Scholar]
- Li, D.; Gong, R.; Wang, H.; Wei, X.; Liu, Z.S.; Qin, D.Q. Analysis of Rotor-Stator Interaction in Turbine Mode of a Pump-Turbine Model. J. Appl. Fluid Mech. 2016, 9, 2259–2268. [Google Scholar] [CrossRef]
- Rodriguez, C.; Egusquiza, E.; Santos, I.F. Frequencies in the Vibration Induced by the Rotor Stator Interaction in a Centrifugal Pump Turbine. J. Fluids Eng. 2007, 129, 1428–1435. [Google Scholar] [CrossRef] [Green Version]
- Trivedi, C.; Cervantes, M.J. Fluid-structure interactions in Francis turbines: A perspective review. Renew. Sustain. Energy Rev. 2017, 68, 87–101. [Google Scholar] [CrossRef]
- Keck, H.; Sick, M. Thirty years of numerical flow simulation in hydraulic turbomachines. Acta Mech. 2008, 201, 211–229. [Google Scholar] [CrossRef]
- Li, C.B.; Jiang, X.Y. Flow Structures in Transitional and Turbulent Boundary Layers. Phys. Fluids 2019, 31, 111301. [Google Scholar] [CrossRef] [Green Version]
- Ortolan, A.; Courty-Audren, S.K.; Binder, N.; Carbonneau, X.; Rosa, N.G.; Challas, F. Experimental and Numerical Flow Analysis of Low-speed Fans at Highly Loaded Wind Milling Conditions. J. Turbomach. 2017, 139, 071009. [Google Scholar] [CrossRef]
- Sanders, D.D.; Nessler, C.A.; Sondergaard, R.; Polanka, M.D.; Marks, C.; Wolff, M.; O’Brien, W.F. A CFD and Experimental Investigation of Unsteady Wake Effects on a Highly Loaded Low Pressure Turbine Blade at Low Reynolds Number. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar]
- Sarkar, S. Influence of Wake Structure on Unsteady Flow in a Low Pressure Turbine Blade Passage. J. Turbomach. 2009, 131, 041016. [Google Scholar] [CrossRef]
- Wissink, J.; Zaki, T.A.; Rodi, W.; Durbin, P.A. The Effect of wake Turbulence Intensity on Transition in a Compressor Cascade. Flow Turbul. Combust. 2014, 93, 555–576. [Google Scholar] [CrossRef] [Green Version]
- Jia, L.; Zou, T.; Zhu, Y.; Lee, C. Rotor boundary layer development with inlet guide vane (IGV) wake impingement. Phys. Fluids 2018, 30, 040911. [Google Scholar] [CrossRef]
- Gete, Z.; Evans, R. An experimental investigation of unsteady turbulent-wake/boundary-layer interaction. J. Fluids Struct. 2003, 17, 43–55. [Google Scholar] [CrossRef]
- Solís-Gallego, I.; Fernández, A.M.; Fernández-Oro, J.; Díaz, K.M.A.; Velarde-Suárez, S. LES-based numerical prediction of the trailing edge noise in a small wind turbine airfoil at different angles of attack. Renew. Energy 2018, 120, 241–254. [Google Scholar] [CrossRef]
- Fernandez-Gamiz, U.; Mármol, M.G.; Rebollo, T.C. Computational Modeling of Gurney Flaps and Microtabs by POD Method. Energies 2018, 11, 2091. [Google Scholar] [CrossRef] [Green Version]
- Thompson, J.F.; Warsi, Z.U.A.; Mastin, C.W. Numerical Grid Generation; Elsevier Science Publishing: London, UK, 1985. [Google Scholar]
- Fluent Inc. User’s Guide; Fluent 16.0; Fluent Inc.: New York, NY, USA, 2016. [Google Scholar]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Zeng, Y.; Yao, Z.; Gao, J.; Hong, Y.; Wang, F.; Zhang, F. Numerical Investigation of Added Mass and Hydrodynamic Damping on a Blunt Trailing Edge Hydrofoil. J. Fluids Eng. 2019, 141, 081108. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables—Part II: Test Cases and Industrial Applications. J. Turbomach. 2004, 128, 423–434. [Google Scholar] [CrossRef]
- Gorji, S.; Seddighi, M.; Ariyaratne, C.; Vardy, A.E.; O’Donoghue, T.; Pokrajac, D.; He, S. A comparative study of turbulence models in a transient channel flow. Comput. Fluids 2014, 89, 111–123. [Google Scholar] [CrossRef] [Green Version]
- Khayatzadeh, P.; Nadarajah, S. Laminar-turbulent flow simulation for wind turbine profiles using the γ–Reθt transition model. Wind Energy 2014, 17, 901–918. [Google Scholar] [CrossRef]
- Furst, J.; Straka, P.; Příhoda, J.; Šimurda, D. Comparison of several models of the laminar/turbulent transition. EPJ Web Conf. 2013, 45, 1–6. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill: Boston, MA, USA, 1979. [Google Scholar]
- Meyer, R.X. The Effect of Wakes on the Transient Pressure and Velocity Distributions in Turbomachines. J. Basic Eng. 1958, 4, 1544–1552. [Google Scholar]
- Halstead, D.E.; Wisler, D.C.; Okiishi, T.H.; Walker, G.J.; Hodson, H.P.; Shin, H.-W. Boundary Layer Development in Axial Compressors and Turbines: Part 1 of 4—Composite Picture. J. Turbomach. 1997, 119, 114–127. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, Y.; Li, W.; Hu, S.; Zhu, J. Effects of periodic wakes on boundary layer development on an ultra-high-lift low pressure turbine airfoil. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 231, 25–38. [Google Scholar] [CrossRef]
- Doligalski, T.L.; Walker, J.D.A. The boundary layer induced by a convected two-dimensional vortex. J. Fluid Mech. 1984, 139, 1–28. [Google Scholar] [CrossRef]

















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, X.; Zhang, X.; Wang, P.; Wang, J.; Xu, Z. Numerical Investigation of the Turbulent Wake-Boundary Interaction in a Translational Cascade of Airfoils and Flat Plate. Energies 2020, 13, 4478. https://doi.org/10.3390/en13174478
Ruan X, Zhang X, Wang P, Wang J, Xu Z. Numerical Investigation of the Turbulent Wake-Boundary Interaction in a Translational Cascade of Airfoils and Flat Plate. Energies. 2020; 13(17):4478. https://doi.org/10.3390/en13174478
Chicago/Turabian StyleRuan, Xiaodong, Xu Zhang, Pengfei Wang, Jiaming Wang, and Zhongbin Xu. 2020. "Numerical Investigation of the Turbulent Wake-Boundary Interaction in a Translational Cascade of Airfoils and Flat Plate" Energies 13, no. 17: 4478. https://doi.org/10.3390/en13174478
APA StyleRuan, X., Zhang, X., Wang, P., Wang, J., & Xu, Z. (2020). Numerical Investigation of the Turbulent Wake-Boundary Interaction in a Translational Cascade of Airfoils and Flat Plate. Energies, 13(17), 4478. https://doi.org/10.3390/en13174478