The Influence of Weather Conditions on the Optimal Setting of Photovoltaic Thermal Hybrid Solar Collectors—A Case Study

Abstract

The potential absorption of solar energy in photovoltaic thermal (PVT) hybrid solar collectors at different tilt angles was compared in the present study. The optimal tilt angles were tested in three variants: during 1 day, 1 year and a period of 30 years. Simulations were performed based on actual weather data for 30 years, including average hourly total radiation, insolation and air temperature. The apparent movement of the Sun across the sky, solar radiation properties, and the electrical and thermal efficiency of a PVT collector were also taken into account in the simulation model. The optimal orientation of the absorber surface was determined by solving an optimization task. The results of the study indicate that in the long-term perspective, the collector’s performance is maximized when the absorber is positioned toward the south at an elevation angle of 34.1°.

1. Introduction

The global economy relies primarily on energy derived from fossil fuels. However, the progressive depletion of fossil fuels and their environmental impact have prompted the search for alternative renewable sources of energy. The transition from fossil fuels to renewable energy (RE) is in its infancy: the share of electricity from renewable sources exceeds 60% in countries that are RE leaders, but it does not exceed a few percent in most countries. In Poland, the share of RE in total energy consumption is only 11.27% [1], and around 85% of electricity is derived from coal (53.6% from bituminous coal and 31.6% from brown coal), whose combustion releases massive amounts of CO₂ into ambient air [2]. The adoption of more stringent environmental protection regulations in EU law will force Poland to replace fossil fuels with effective RE sources.

The rapid development of solar technology could offer a solution to this problem [3]. The solar energy flux reaching the surface of the Earth is several thousand times higher than the present consumption of solar energy [4]. However, solar energy dissipation poses a considerable obstacle because the amount of energy that reaches the Earth per unit area is relatively low. Solar irradiance also varies considerably on a yearly, monthly and daily basis. This is determined by geographical location as well as climate. The low effectiveness and high cost of solar-powered equipment create additional problems. For these reasons, solar energy accounts for less than 1% of total energy from RE sources, and it does not exceed 0.3% in Poland [5].

Solar energy might be the most promising source of RE that can be converted to thermal and electrical energy. There are two main types of devices for harnessing the energy of the Sun: solar thermal collectors and photovoltaic (PV) panels. Recent years have witnessed the development of hybrid devices that convert solar energy into both heat and electricity [6,7,8,9,10]. These solutions have numerous advantages because only approximately 15% of solar irradiance is converted into electricity, and the remainder is reflected and converted into heat that is accumulated by the collector (up to 60%) [11,12]. Excess heat from the PV module can be harnessed to produce heat, which can increase energy conversion efficiency by 10–15% [13,14].

The conversion efficiency of solar panels is influenced by numerous factors, such as the type of device, the applied technology and materials [15,16,17,18], solar radiation parameters [19,20,21,22] and weather conditions (ambient temperature, wind and particulate pollution) [23,24,25,26,27,28]. From the practical point of view, these parameters are largely variable and independent because users can only control the collector’s orientation relative to the angle at which the incoming insolation strikes the absorber [29,30,31,32,33,34]. Automatic solar tracking systems for orienting the panel continuously toward the Sun [35,36,37,38,39] and seasonal tilt angles have been extensively studied in the literature [40,41,42,43,44]. Automatic tracking systems increase the amount of harnessed solar energy, but their economic efficiency continues to pose a challenge [45,46].

A well-known and well-described topic is the optimization of the absorber positioning angles determined independently for thermal collectors and PV cells. In the case of hybrid collectors (photovoltaic thermal, PVT), the situation becomes more complex due to the different influences of ambient temperature, solar spectrum and the proportion of diffuse radiation. Therefore, the main aim of this study was to determine the optimal, time-invariant position of the absorber plane (with the simultaneous conversion of solar radiation into heat and electricity) in view of the actual characteristics of solar radiation and weather conditions.

2. Materials and Methods

In this study, digital simulations were performed with the use of:

• Long-term meteorological data for the analyzed location;
• Operating parameters of a photovoltaic thermal (PVT) hybrid solar collector; and
• A mathematical model developed for data simulation.

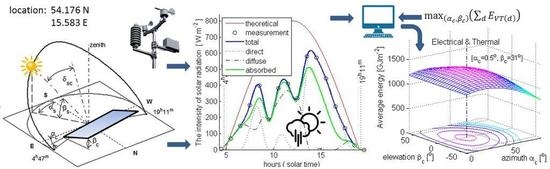
2.1. Location and Meteorological Data

In Europe, total solar irradiance increased at a rate of 1.0% per decade in 1987–2002 [47] and 2.2% per decade in 1985–2005 [48], which favored the development of solar-powered equipment. The above trends were also confirmed by Polish studies [49].

The following criteria were used to select the location for optimizing the tilt angle of a PVT hybrid solar collector: number of sunshine hours, total monthly and annual radiation, atmospheric transmissivity, and duration of uninterrupted insolation. In Poland, these criteria are met in the coastal region, which is characterized by the highest total insolation and the highest number of sunshine hours between April and September. The coastal region receives more than 70% of average annual insolation, which exceeds 3800 MJ·m⁻² in Kołobrzeg (15°35′ E, 54°10′ N); therefore, it is particularly suited to the needs of insolation analyses [50]. This study relied on long-term weather data collected by the Hydrological and Meteorological Station in Kołobrzeg (Institute of Meteorology and Water Management, Kołobrzeg, Poland) over a period of 30 years between 1 January 1986 and 31 December 2015. The following data were analyzed: average hourly total radiation, insolation (according to Niedźwiedź [51]) and air temperature. The influence of wind speed and wind direction was intentionally disregarded because the values registered by the meteorological station generally do not reflect local conditions (landform, plant cover, buildings and structures) [46,52,53]. Meteorological data were processed by spline interpolation with a time step of $∆t=60$ s. Exemplary results are presented in Figure 1.

2.2. Photovoltaic Thermal Hybrid Solar Collectors

Photovoltaic thermal (PVT) hybrid solar collectors convert solar energy into both electricity and heat. Various types of PVT hybrid collectors have been developed [54,55,56,57], and most of them are liquid-cooled uncovered devices [58,59,60].

Most PVT hybrid solar collectors and photovoltaic modules are certified for compliance with the IEC 61215 standard. The performance of PV solar panels is evaluated under the Standard Test Conditions (STC), where irradiation on the solar panel is 1000 W/m² and ambient temperature is 25 °C. The Nominal Operating Cell Temperature (NOCT) accounts for environmental factors that affect the performance of solar panels. The NOCT is based on the following standard reference conditions: irradiation on the solar panel 800 W·m⁻², air temperature 20 °C and wind velocity 1 m·s⁻¹. The thermal performance of PVT hybrid solar collectors is less standardized, and the relevant conditions are often not sufficiently defined. The available solutions can be compared based on the EN 12975 standard for assessing the performance of solar collectors—in particular, panels with the Solar Keymark certificate [61]. PVT hybrid solar collectors combine elements of thermal solar collector technology and PV modules; therefore, they have to meet the requirements of standard EN 12975 for glazed solar collectors as well as standard IEC 61215 for PV modules [62].

2.3. Mathematical Model

The apparent movement of the Sun across the sky, solar radiation properties and the electrical and thermal efficiency of a PVT collector were also taken into account in the mathematical model.

2.3.1. Apparent Movement of the Sun across the Sky

Various algorithms for calculating the apparent movement of the Sun across the sky have been proposed in the literature, including simple [63,64] and more complex solutions [65,66,67,68]. The developed algorithms differ in accuracy and validity period, and local landform is also taken into account in some solutions to compute sunrise and sunset times [69]. This study relied on one of the five algorithms (no. 2) proposed by Grena [70] for calculating angles ${\alpha }_c\left(t\right)$ and ${\beta }_c\left(t\right)$ with a precision of 0.034°. The visualization of data for a selected day of the year 2006 is presented in Figure 2a.

2.3.2. Solar Radiation Properties

Total radiation and insolation are the most important solar radiation properties. Total radiation is the sum of direct and diffuse solar radiation. In Poland, the proportion of diffuse solar radiation in total radiation ranges from around 47% in summer to 70% in winter. Diffuse radiation data are not easily available, and this parameter is estimated with the use of various models based on general meteorological observations [71,72,73,74]. These models account for latitude, solar declination angle, elevation, length of day and atmospheric transmissivity [75].

Diffuse solar irradiance $I_{\mathrm{s}}$ was calculated based on the extrapolated values of solar flux density and insolation [76]:

$$I_{\mathrm{s}}\left(t\right)=\left(1-k_{\mathrm{d}}\left(t\right)\right)I_{\mathrm{t}}\left(t\right)$$

(1)

where: $I_{\mathrm{t}}\left(t\right)$ is the instantaneous solar flux density incident on 1 m² of a horizontal surface per second; and $k_{\mathrm{d}}\left(t\right)$ is the insolation (instantaneous direct solar radiation in 1 h, measured at 0.1-h intervals).

Based on the absorber’s orientation relative to the Sun, which is described by the solar azimuth angle ${\alpha }_{\mathrm{c}}$ and the solar elevation angle ${\beta }_{\mathrm{c}}$ (Figure 2a), as well as the assumption that the diffuse fraction of solar radiation is isotropic and uniform over the sky dome [77], total radiance incident on the absorber surface is described by the following formula:

$$I_a=I_{\mathrm{t}}·\left[k_{\mathrm{d}}·\cos \left({\delta }_{\mathrm{sc}}\right)+\frac{\left(1-k_{\mathrm{d}}\right)}{2}·\left(1+\cos \left({\beta }_{\mathrm{c}}\right)\right)\right],$$

(2)

where ${\delta }_{\mathrm{sc}}$ is the solar incidence angle (the angle between the Sun’s rays and the normal on the absorber surface), which is determined by the scalar product of unit vectors $\overrightarrow{e_{\mathrm{s}}}$ and $\overrightarrow{e_{\mathrm{c}}}$:

$${\delta }_{\mathrm{sc}}=\mathrm{arc}\cos \left(\overrightarrow{e_{\mathrm{s}}}\circ \overrightarrow{e_{\mathrm{c}}}\right)$$

(3)

where $\overrightarrow{e_{\mathrm{s}}}$ denotes the direction of the Sun’s rays:

$$\overrightarrow{e_{\mathrm{s}}}=\left[\sin \left({\beta }_{\mathrm{s}}\right)\cos \left({\alpha }_{\mathrm{s}}\right), \sin \left({\phi }_{\mathrm{s}}\right)\sin \left({\alpha }_{\mathrm{s}}\right), \cos \left({\beta }_{\mathrm{s}}\right)\right],$$

(4)

and vector $\overrightarrow{e_{\mathrm{c}}}$ is perpendicular to the absorber surface:

$$\overrightarrow{e_{\mathrm{c}}}=\left[\sin \left({\alpha }_{\mathrm{c}}\right), -\cos \left({\alpha }_{\mathrm{c}}\right), 0\right]\times \left[\sin \left({\beta }_{\mathrm{c}}\right)\cos \left({\alpha }_{\mathrm{c}}\right), \sin \left({\beta }_{\mathrm{c}}\right)\sin \left({\alpha }_{\mathrm{c}}\right), \cos \left({\beta }_{\mathrm{c}}\right)\right]$$

(5)

Daily fluctuations in solar irradiance on a selected day of the year and the orientation of the absorber surface of a PVT collector are presented in Figure 2b. The daily distribution of solar radiation is determined by daytime length, the altitude of the Sun above the horizon (Figure 2a), cloud cover and cloud type, and atmospheric transparency. The differences between real and theoretical solar irradiance in Figure 2b are caused mainly by cloud cover. Considerable cloud cover, particularly in summer, results from enhanced cyclone activity in northern Europe (North Sea and Baltic Sea), and in colder parts of the year—from cyclogenesis in the Mediterranean Region and the Black Sea region [78]. The average number of cloudy days in Poland is estimated to be between 110 and 200 [79].

2.3.3. Performance Parameters of PVT Collectors

If the solar energy received by the absorber ($I_{\mathrm{a}}$) is first converted into electricity [80], the power output of a PV module $P_{\mathrm{V}}$ is calculated as follows:

$$P_{\mathrm{V}}={\eta }_{\mathrm{V}}·I_{\mathrm{a}}·A.$$

(6)

The thermal output $P_{\mathrm{T}}$ of a thermal module is determined using the following formula:

$$P_{\mathrm{T}}={\eta }_{\mathrm{T}}·I_{\mathrm{a}}·\left(1-{\eta }_{\mathrm{V}}\right)·A$$

(7)

and the combined electrical and heat output $P_{\mathrm{VT}}$ of a PVT hybrid solar collector is calculated as:

$$P_{\mathrm{VT}}=\left({\eta }_{\mathrm{V}}+{\eta }_{\mathrm{T}}-{\eta }_{\mathrm{V}}·{\eta }_{\mathrm{T}}\right)·I_{\mathrm{a}}·A$$

(8)

where ${\eta }_{\mathrm{V}}$ is the PV module efficiency; ${\eta }_{\mathrm{T}}$ is the thermal module efficiency; and $A$ is the absorber surface area. The efficiency of the PV module ${\eta }_{\mathrm{V}}$ at the given values of solar energy $I_{\mathrm{a}}$ and module temperature ${\vartheta }_{\mathrm{m}}$ is calculated with the following formula [59]:

$${\eta }_{\mathrm{V}}={\eta }_{\mathrm{V}}^{\mathrm{STC}}·\left[1-0.04·\ln \left(\frac{I_{\mathrm{a}}}{1000\mathrm{W}·{\mathrm{m}}^{-2}}\right)-{\gamma }_{\mathrm{V}}^{\mathrm{STC}}·\left({\vartheta }_{\mathrm{m}}-25{ }^{°}\mathrm{C}\right)\right]$$

(9)

where ${\eta }_{\mathrm{V}}^{\mathrm{STC}}$ and ${\gamma }_{\mathrm{V}}^{\mathrm{STC}}$ denote the efficiency and the temperature coefficient of a PV module based on STC. For crystalline silicon PV modules, the value of ${\gamma }_{\mathrm{V}}^{\mathrm{STC}}$ ranges from 0.0037 to 0.0052 °C⁻¹. The module’s operating temperature ${\vartheta }_{\mathrm{m}}$ is determined by its structure as well as weather conditions. The above parameters have been discussed extensively by Akhsassi et al. [81]. A PV module compliant with NOCT parameters was tested in this study:

$${\vartheta }_{\mathrm{m}}={\vartheta }_{\mathrm{a}}+I_{\mathrm{a}}·\frac{\mathrm{NOCT}-20}{800 \mathrm{W}·{\mathrm{m}}^{-2}}$$

(10)

where ${\vartheta }_{\mathrm{a}}$ is the ambient temperature and NOCT is 42 to 46 °C.

The efficiency of the thermal module ${\eta }_{\mathrm{T}}$ varies in different types of collectors. In covered PVT hybrid solar collectors (liquid-cooled or air-cooled with a closed air circuit), thermal efficiency is determined with the use of the following formula [77,82]:

$${\eta }_{\mathrm{T}}={\eta }_0-\frac{1}{I_{\mathrm{a}}·\left(1-{\eta }_{\mathrm{V}}\right)} [a_1·\left({\vartheta }_{\mathrm{m}}-{\vartheta }_{\mathrm{a}}\right)+a_2·{\left({\vartheta }_{\mathrm{m}}-{\vartheta }_{\mathrm{a}}\right)}^2]$$

(11)

where ${\eta }_0$ is the maximum thermal efficiency; $a_1$ is the linear heat loss coefficient; and $a_2$ is the quadratic heat loss coefficient.

2.4. Simulations

Numerical calculations were performed based on the average operating parameters of liquid-cooled PVT collectors [59,83]: ${\eta }_0=0.50$, $a_1=5 \mathrm{W}{\left({\mathrm{m}}^2{ }^{°}\mathrm{C}\right)}^{-1}$, $a_2=0.02 \mathrm{W}{\left(\mathrm{m}{ }^{°}\mathrm{C}\right)}^{-2}$, ${\eta }_{\mathrm{V}}^{\mathrm{STC}}=0.16$, ${\gamma }_{\mathrm{V}}^{\mathrm{STC}}=0.0045{ }^{°}{\mathrm{C}}^{-1}$ and $\mathrm{NOTC}=44{ }^{°}\mathrm{C}$ [84].

The objective of the model was to provide information about the potential amount of solar energy that can be converted by 1 m² of absorber surface area into electricity $E_{\mathrm{V}}$, heat $E_{\mathrm{T}}$, and both electricity and heat $E_{\mathrm{VT}}$ in:

• One day

  $$E_{\mathrm{V}\left(d\right)}=\underset{t=t_{\mathrm{ss}}}{\overset{t_{\mathrm{sr}}}{{\displaystyle \int }}}{P}_{\mathrm{V}\left(d\right)} dt; E_{\mathrm{T}\left(d\right)}=\underset{t=t_{\mathrm{ss}}}{\overset{t_{\mathrm{sr}}}{{\displaystyle \int }}}{P}_{\mathrm{T}\left(d\right)} dt; E_{\mathrm{VT}\left(d\right)}=\underset{t=t_{\mathrm{ss}}}{\overset{t_{\mathrm{sr}}}{{\displaystyle \int }}}{P}_{\mathrm{VT}\left(d\right)} dt,$$

  (12)

  where t_ss and t_sr are sunrise and sunset time, and d is the day of the year;
• One year

  $$E_{\mathrm{V}\left(y\right)}={{\displaystyle \sum }}_{d=1}^{365\left(366\right)}{E}_{\mathrm{V}\left(d\right)}; E_{\mathrm{T}\left(y\right)}={{\displaystyle \sum }}_{d=1}^{365\left(366\right)}{E}_{\mathrm{T}\left(d\right)}; E_{\mathrm{VT}\left(y\right)}={{\displaystyle \sum }}_{d=1}^{365\left(366\right)}{E}_{\mathrm{VT}\left(d\right)};\mathrm{and}$$

  (13)
• The analyzed period of 30 years

  $$E_{\mathrm{V}\left(\mathrm{all}\right)}={{\displaystyle \sum }}_{y=1986}^{2015}{E}_{\mathrm{V}\left(y\right)}; E_{\mathrm{T}\left(\mathrm{all}\right)}={{\displaystyle \sum }}_{y=1986}^{2015}{E}_{\mathrm{T}\left(y\right)}; E_{\mathrm{VT}\left(\mathrm{all}\right)}={{\displaystyle \sum }}_{y=1986}^{2015}{E}_{\mathrm{VT}\left(y\right)}.$$

  (14)

The optimal orientation of the absorber surface was determined by solving an optimization task, where the absorber’s azimuth angle ${\alpha }_{\mathrm{c}}$ and elevation angle ${\beta }_{\mathrm{c}}$ were the decision criteria, and the amount of solar energy converted into electricity $E_{\mathrm{V}}$, heat $E_{\mathrm{T}}$ and both electricity and heat $E_{\mathrm{VT}}$ were the optimization criteria:

$$\underset{({\alpha }_{\mathrm{c}},{\beta }_{\mathrm{c}})}{\max }({\displaystyle \sum }_d{E}_{\mathrm{V}\left(d\right)}); \underset{({\alpha }_{\mathrm{c}},{\beta }_{\mathrm{c}})}{\max }({\displaystyle \sum }_d{E}_{\mathrm{T}\left(d\right)}); \underset{({\alpha }_{\mathrm{c}},{\beta }_{\mathrm{c}})}{\max }({\displaystyle \sum }_d{E}_{\mathrm{VT}\left(d\right)}).$$

(15)

The entire mathematical model was implemented in the MATLAB R2014a environment (Math Works, Natick, MA, USA). Data were simulated with a time step of ∆t = 60 s. A block diagram presenting all stages of the simulation process is presented in Figure 3.

3. Results and Discussion

The results of the study indicate that the absorber’s optimal azimuth angle ${\alpha }_{\mathrm{c}\left(\mathrm{opt}\right)}$ and elevation angle ${\beta }_{\mathrm{c}\left(\mathrm{opt}\right)}$ are determined by the daily distribution of solar radiation, insolation, ambient temperature, and the solar energy conversion method. Both angles change with an increase in insolation, and the absorber is positioned perpendicular to the direction of the Sun, which corresponds to the highest direct solar irradiance. In turn, when the proportion of diffuse solar irradiance increases, azimuth angle ${\alpha }_{\mathrm{c}}$ is less significant, and the horizontal orientation of the absorber (${\beta }_{\mathrm{c}}\to 0$) plays a more important role.

For the daily distribution of solar radiation indicated in Figure 2 (extensive cloud cover before noon), the optimal angles are ${\alpha }_{\mathrm{c}\left(\mathrm{opt}\right)}=29.6{}^{°}$ and ${\beta }_{\mathrm{c}\left(\mathrm{opt}\right)}=33.7{}^{°}$ (Figure 4c). These angles would be determined at ${\alpha }_{\mathrm{c}\left(\mathrm{opt}\right)}=0{}^{°}$ and ${\beta }_{\mathrm{c}\left(\mathrm{opt}\right)}=42.6{}^{°}$ if all hours in the analyzed day were sunshine hours. The minor differences in the optimal orientation of an absorber that converts solar energy to electricity only (Figure 4a) or heat only (Figure 4b) result from the daily distribution of temperature and its influence on conversion efficiency described by Equations (9) and (11).

Daily cloud cover and insolation data are averaged for longer periods of time (1 year: Figure 5; many years: Figure 6), and diffuse solar radiation accounts for around 31% of the overall balance. The time shift (around 2 h) between the maximum daily temperature and the maximum daily solar radiation remains unchanged (Figure 7a). The observed time shift can be attributed to the fact that radiation is absorbed by air and the surface of the Earth, which leads to thermal inertia. The collector’s performance can be optimized by positioning the absorber towards the south (${\alpha }_{\mathrm{c}\left(\mathrm{opt}\right)}=0.5{}^{°}$) at an elevation angle of ${\beta }_{\mathrm{c}\left(\mathrm{opt}\right)}=34.1{}^{°}$ (Figure 6). However, if we account for the flat shape of the curve (Figure 5 and Figure 6) near the optimal point, and if we assume that the generated energy does not differ by more than 1% from the maximum output, the optimal azimuth angle is ${\alpha }_{\mathrm{c}\left(\mathrm{opt}\right)}=0.5\pm 20{}^{°}$, and the optimal elevation angle is ${\beta }_{\mathrm{c}\left(\mathrm{opt}\right)}=34.1\pm 8.5{}^{°}$.

The optimal annual settings for the absorber surface, determined in the study, were compared with the values calculated in the Photovoltaic Geographical Information System (PVGIS) [85]. Depending on the applied PVGIS database (SARAH, CMSAF, ERA5, COSMO) and PV technology, the optimal azimuth angle was determined in the range of ${\alpha }_{\mathrm{c}}=-1{}^{°}$ to ${\alpha }_{\mathrm{c}}=3{}^{°}$, and the optimal elevation angle in the range of ${\beta }_{\mathrm{c}}=39{}^{°}$ to ${\beta }_{\mathrm{c}}=43{}^{°}$. The elevation angle calculated in the study is much smaller, which indicates that local cloud cover and, consequently, diffuse radiation significantly influence absorber settings. Cloud cover also affects electricity generation. In the proposed model, the annual energy output is determined at 0.52 ± 0.02 GJm⁻² on average (Figure 7c), around 0.12 GJm⁻² less than that calculated for sunny days. The above applies to the values calculated in the proposed model (from 0.62 to 0.68 GJm⁻²) as well as those computed in PVGIS (from 0.60 to 0.70 GJm⁻²).

The fact that electricity and heat can be generated simultaneously is an unquestioned advantage of PVT hybrid solar collectors (Figure 7c). Hybrid collectors generate less thermal energy (around 60% per year) than conventional solutions [46]. Nonetheless, heat generation should be regarded as an additional benefit, and it also increases the efficiency of the PV cell.

4. Conclusions

The results of the simulation validate the assumption that in addition to insolation, the daily distribution of solar radiation and temperature also influence the optimal orientation of a PVT hybrid solar collector. If local conditions are taken into account, the calculated values can significantly deviate from the average values of satellite measurements. The above applies to the absorber’s orientation as well as its energy output.

In this study, local conditions were evaluated a posteriori, which implies that the optimal orientation of a PVT hybrid solar collector should be determined based on an analysis of long-term historical meteorological data at the installation site. The absorber’s optimal orientation can also be affected by other factors that were not taken into account in this study, including wind speed, wind direction, topography and plant cover.

It should also be noted that the orientation of the absorber surface was determined based on several optimization criteria to maximize the annual energy output. In the evaluated location, the amount of solar radiation reaching the surface of the Earth is unevenly distributed during the year (it is nearly eight times lower in winter than in summer; Figure 7b). Therefore, a strategy where the differences in energy output across months are leveled out could be adopted as an alternative optimization criterion. The proposed model supports the selection of other optimization criteria and limitations than the available tools, including the PVGIS calculator.