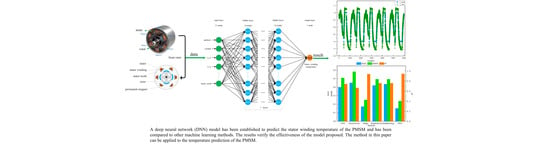
Predicting Temperature of Permanent Magnet Synchronous Motor Based on Deep Neural Network

Abstract

The heat loss and cooling modes of a permanent magnet synchronous motor (PMSM) directly affect the its temperature rise. The accurate evaluation and prediction of stator winding temperature is of great significance to the safety and reliability of PMSMs. In order to study the influencing factors of stator winding temperature and prevent motor insulation ageing, insulation burning, permanent magnet demagnetization and other faults caused by high stator winding temperature, we propose a computer model for PMSM temperature prediction. Ambient temperature, coolant temperature, direct-axis voltage, quadrature-axis voltage, motor speed, torque, direct-axis current, quadrature-axis current, permanent magnet surface temperature, stator yoke temperature, and stator tooth temperature are taken as the input, while the stator winding temperature is taken as the output. A deep neural network (DNN) model for PMSM temperature prediction was constructed. The experimental results showed the prediction error of the model (MAE) was 0.1515, the RMSE was 0.2368, the goodness of fit (R²) was 0.9439 and the goodness of fit between the predicted data and the measured data was high. Through comparative experiments, the prediction accuracy of the DNN model proposed in this paper was determined to be better than other models. This model can effectively predict the temperature change of stator winding, provide technical support to temperature early warning systems and ensure safe operation of PMSMs.

1. Introduction

The thermal loss and cooling modes of the permanent magnet synchronous motor (PMSM) directly affect its temperature rise [1,2,3]. The heat loss of the PMSM mainly includes copper loss, iron loss and mechanical loss. The iron loss mainly depends on the stator’s voltage, and the mechanical loss mainly depends on the rotor speed. Different from iron loss and mechanical loss, the copper loss of a permanent magnet motor stator directly affects the heating degree of the stator winding. On one hand, the heat of the stator winding is first transferred to the insulation. On the other hand, compared with the winding and core, the insulation in the motor is the material with the worst heat resistance among all materials of the motor. In the engineering field, the selection of an insulation grade of PMSM depends entirely on the temperature of the stator winding. When the temperature of the motor stator winding is too high, the insulation will be thermally aged, and decortication will even occur, which will seriously threaten the safe operation of the motor. In addition, if the permanent magnet motor winding heating cannot be effectively controlled, the heat of the stator winding will be further transmitted to the rotor side through the air gap, which will cause irreversible demagnetization of the permanent magnet. In conclusion, accurate evaluation and prediction of stator winding temperature is of great significance to the safety and reliability of permanent magnet motors.

In order to ensure safe operation, many experts and scholars have put forward methods to measure the temperature of a PMSM. Wallscheid et al. used an accurate flux observer in the fundamental wave domain that can indirectly obtain magnet temperature without any additional sensors or signal injections [4]. Mohammed et al. proposed a new sensing method, namely, investigating the application of dedicated electrically non-conductive and electromagnetic interference immune fiber Bragg grating (FBG) temperature sensors embedded in PMSM windings to enable winding open-circuit fault diagnosis based on observing the fault thermal signature [5,6]. However, when these methods are used to measure the temperature of a PMSM, a lot of experimental preparation is needed, which leads to high costs and tedious processes. For this reason, many scholars have begun to consider how to predict temperature after collecting enough data.

The traditional motor temperature prediction model mainly uses the finite element method [7,8]. The specific method is to simulate the transient temperature by using the finite element method, establish the temperature field, and then predict the motor temperature. This method can only be used to calculate and process the current linear data, but it cannot deal with a large number of nonlinear historical data. On the other hand, the method based on machine learning can effectively solve this problem, and the overall prediction effect can be greatly improved compared with the traditional methods. Many experts and scholars have done a lot of research and tried a lot of different methods using machine learning to predict motor temperature. Chen et al. used support vector machine to predict the hot spot temperature of an oil-immersed transformer, and verified its practicability and effectiveness on a large power transformer [9]. Hyeontae et al. used a variety of machine learning methods including decision tree to predict the end temperature of a Linz–Donawiz converter, which was used to improve the quality of melted pig iron. They injected pure oxygen into hot metal in order to remove impurities via oxidation-reduction reactions. The relevant simulation results were presented and compared with the real temperature [10]. The rise of ensemble learning has greatly promoted the development of motor temperature prediction models. Wang applied the stochastic forest method to the temperature prediction of a ladle furnace. The sample was divided into several subsets and the random forest method was applied to obtain higher accuracy than the other temperature models [11]. Zhukov et al. used ensemble methods of classification to assess power system security. The proposed hybrid approach was based on random forest models and boosting models. The experiment results showed that the proposed model can be employed to examine whether a power system is secure under steady-state operating conditions [12]. Su et al. integrated an extreme learning machine to establish a prediction model of iron temperatures in a blast furnace, and selected the corresponding influencing factors as input, combined with several extreme learning machines with different parameters This model achieved high prediction accuracy and generalization performance for molten iron temperature prediction [13].

In recent years, people have paid more and more attention to deep learning methods. The feature extraction of machine learning methods mainly depends on humans. For specific simple tasks, manual feature extraction is simple and effective, but for complex tasks, how to choose appropriate features can be an extremely difficult problem. The feature extraction of deep learning does not rely on manual extraction, and features are automatically extracted by the machine, which is often called end-to-end learning [14]. Therefore, deep learning methods have better versatility. Chinnathambi et al. established three kinds of deep neural network (DNN) to predict the day-head price of the Iberian electricity market [15]. Kasburg et al. used an Long Short Term Memory (LSTM) neural network to predict the photovoltaic power generation of an active solar tracker, and the results were promising [16]. Tao et al. proposed a short-term forecasting model based on deep learning for PM2.5 concentrations [17]. Sengar et al. combined the DNN with a chicken swarm optimization algorithm to realize the load forecasting problem of a wind power generation system [18]. Gui et al. proposed a multi-step time feature selection optimization model of temperature based on the DNN and genetic algorithm (GA), which effectively predicted the temperature of a reheater system [19]. Because of their strong learning ability, wide coverage and good adaptability, deep learning methods have been widely used in various fields.

However, deep learning methods have barely been applied in PMSM temperature prediction. In this paper, the prediction of stator winding temperature in PMSMs is studied. A PMSM consists of two key components, a rotor with a permanent magnet and a stator with properly designed windings. Figure 1 shows the structure of the PMSM. When the PMSM is operating, the temperature of the stator winding will rise due to the influence of copper loss. If the temperature is too high, the insulation will be thermally aged, and in serious cases, it will be shelled, threatening the safe operation of the motor. If the heat is transferred to the rotor side for a long time, it may cause irreversible demagnetization of the permanent magnet, which means the total destruction of the PMSM. This paper only uses a data-driven method to study the thermal management system of PMSMs, and provides a new research method as a means of aiding design and analysis of PMSMs. The main purpose of this study is to establish a stator winding temperature prediction model for PMSMs based on DNN and to verify its effectiveness.

This study employs the following structure. Section 2 introduces the basic structure of the DNN and establishes a PMSM stator winding temperature prediction model. In Section 3, the dataset used in this paper is introduced and the prediction performance of the proposed model is presented. Conclusions and prospections are drawn in Section 4.

2. Method Based on DNN

2.1. Establishment of a Stator Winding Temperature Prediction Model for PMSMs

There are many factors that after the stator winding temperature of a PMSM. In this paper, 11 variables are regarded as input, including ambient temperature (ambient), coolant temperature (coolant), direct-axis voltage (u_d), quadrature-axis voltage (u_q), motor speed (motor_speed), torque, direct-axis current (i_d), quadrature-axis current (i_q), permanent magnet surface temperature (pm), stator yoke temperature (stator_yoke) and stator tooth temperature (stator_tooth). Stator winding temperature (stator_winding) is regarded as output. Considering the high dimension of the independent variables, a DNN model was chosen for the prediction.

DNN is an extension of an artificial neural network (ANN), with a structure that is similar to ANN but with a number of hidden layers [20,21,22,23]. Generally, neural networks that have two or more hidden layers can be regarded as a DNN. Figure 2 shows the structures of ANNs and DNNs.

In this paper, the PMSM stator winding temperature prediction model based on a DNN has nine layers. The first layer is the input layer, and the number of its nodes is equal to the number of input variables X (i.e., 11). The ninth layer (in other words, the last layer) is the output layer. The number of its nodes is equal to the number of output-dependent variable y, which equals 1. The layers from the second to the eighth are hidden layers, and each of them has 14 nodes, respectively. The nodes of the former layer are connected with each node of the latter layer, one by one, and there are no connections between nodes of the same layer. The activation function of a hidden layer is the ReLU function, and the activation function of the output layer is the tanh function. The loss function of the model is the mean squared error (MSE) function, and the back propagation algorithm is the Adam optimization algorithm, whose learning rate is set to 0.001. Figure 3 shows the DNN model constructed in this paper.

The constructed neural network model was used to predict the PMSM stator winding temperature. Figure 4 shows the prediction process. First of all, the data were standardized, then the standardized data were divided into five equal parts by means of five-fold cross validation. Each part was taken as the test set in turn, while the other four parts were used as the training set. The DNN model used the training set to fit the model while the test set was used to predict the stator winding temperature. The results of the DNN model were consolidated; thus, the 6000 pieces of predicted values were obtained. Together with the real values, the metrics of the DNN model could be calculated.

2.2. Assessment of Model

In this paper, the average absolute error (MAE), root mean squared error (RMSE) and goodness of fit (R²) were selected as metrics to evaluate the prediction performance of the model.

MAE is the average value of the absolute error, which reflects the actual situation of the deviation between the predicted value and the real value. MAE is generally used to measure the error of the predicted value deviating from the real value, and the smaller the MAE value, the better the prediction performance. Assuming $y_{true}^t$ represents the actual value, $y_{pred}^t$ represents the predicted value and $N$ represents the number of samples. Equation (1) is the calculation formula of MAE.

$$MAE=\frac{1}{N}{\displaystyle \sum _{t=1}^N\left|y_{pred}^t-y_{true}^t\right|}$$

(1)

RMSE is the square root of the ratio of the square of the deviation between the predicted value and the real value and the number of samples. It is often used as a measure of the prediction results of machine learning models. Similar to the MAE, the smaller the RMSE value, the better the prediction performance. Equation (2) is the calculation formula of the RMSE.

$$RMSE=\frac{1}{N}{\displaystyle \sum _{t=1}^N\left(y_{true}^t-y_{pred}^t\right)}$$

(2)

R² is the goodness of fit, which measures the ability of the prediction model to fit the data. Its range is 0–1. The closer the value to 1, the higher the fitting degree is, and the better the prediction performance of the model is. Equation (3) is the calculation formula of the R².

$$R^2=1-\frac{{\displaystyle \sum _{t=1}^N{\left(y_{true}^t-y_{pred}^t\right)}^2}}{{\displaystyle \sum _{t=1}^N{\left(y_{true}^t-y_{avg}\right)}^2}}$$

(3)

3. Experimental Results and Discussion

3.1. Introduction of Dataset

The data used in this study were collected from the PMSM placed on a test bench. The PMSM was a German prototype from the original equipment manufacturer. The measuring platform was assembled by the LEA department of Paderborn University [24,25,26,27]. The main purpose of recording the dataset was to simulate the temperatures of the stator and rotor in real time. Figure 5 shows a random selection of 6000 pieces of the data from this dataset.

The main features of the selected dataset are as follows:

• ambient—the ambient temperature is measured by a temperature sensor located close to the stator;
• coolant—temperature of the coolant. The motor is cooled by water. The measurement is performed at the outflow of water;
• u_d—voltage of the d-component;
• u_q—voltage of the q-component;
• motor_speed—engine speed;
• torque—torque induced by current;
• i_d—current of the d-component;
• i_q—current of the q-component;
• pm—surface temperature of the permanent magnet, which is the temperature of the rotor;
• stator_yoke—the stator yoke temperature is measured using a temperature sensor;
• stator_tooth—the temperature of the stator tooth is measured using a temperature sensor;
• stator_winding—the temperature of the stator winding is measured using a temperature sensor.

The test conditions for the dataset were as follows:

• all recordings were selected at a frequency of 2 Hz (one row in 0.5 s);
• the engine was accelerated using manually designed driving cycles indicating the reference engine speed and reference torque;
• currents in the d/q coordinates (columns “i_d” and “i_q”) and voltages in the coordinates d/q (columns “u_d” and “u_q”) were the result of a standard control strategy that tried to follow the reference speed and torque;
• the columns “motor_speed” and “torque” are the resulting values achieved by this strategy, obtained from the specified currents and voltages.

In machine learning, if the variance of a feature is several orders of magnitude different from other features, it will occupy a dominant position in the learning algorithm, resulting in the learner not being able to learn from other features as expected. Data standardization can readjust the original data so that they have the properties of standard normal distribution. The processing of standardization is shown as Equation (4):

$$x_{std}^i=\frac{x_i-{\mu }_x}{{\delta }_x}$$

(4)

where, $x_{std}^i$ represents the standardized result, $x_i$ represents the original data, ${\mu }_x$ represents the mean value and ${\delta }_x$ represents the standard deviation.

3.2. Prediction Results of the Model

The specification of the computer used in this experiment was a dual-channel Intel E5 2690 V2 CPU with 128 GB DDR-RAM, which was manufactured by ASUS and made in Taiwan, China. The programming language was Python, and the model used was the DNN model built in Section 3.3. After the dataset in Figure 5 was standardized, 6000 pieces of data were divided into five equal parts by means of five-fold cross validation. Each part was taken as the test set in turn, and the other four parts were used as the training set. Thus, all the data served as both the training set and test set. Taking the stator winding temperature as dependent variable y and the remaining 11 variables as independent variables X, the PMSM stator winding temperature could be predicted.

The curve of the MSE loss value with the number of iterations of the model’s training set is shown in Figure 6. It can be seen that the loss value of the training set decreases rapidly during the first 10 iteration cycles, while it decreases slowly in the later iteration cycles.

Figure 7 shows the prediction results of the model. Figure 7a presents a comparison between the predicted values and the real values of the model. It can be seen that there are many overlapped parts between predicted values and real values. In this paper, the established DNN selected tanh as the activation function of output layer among sigmoid, ReLU (Rectified Linear Unit) and tanh, which had the best performance on the dataset. The output value of the tanh activation function was between −1 and 1, and therefore the values of y_pred in Figure 7a range from −1 to 1, resulting in local saturation when the values of y_true were out of the range. Figure 7b shows a comparison between the predicted and real values after the dataset was normalized, and it can be seen that the curves of y_pred and y_true are almost coincident. Figure 7c,d shows the absolute errors and absolute percentage errors, respectively. The absolute errors are always lower than 0.6 °C, while the absolute percentage errors are barely higher than 10%. The results indicate the model has great prediction performance.

3.3. Comparison with Other DNN Models

The network topology of a DNN consists of the number of hidden layers, a number of neurons in each hidden layer, an activation function of the output layer and hidden layers, the learning rate and so on, all of which play very important roles in the prediction performance of the DNN. A DNN with unsuitable topology will not only increase the training time, but also lead to overfitting or underfitting.

In order to compare it more fairly with other models, instead of employed normalization and anti-normalization methods, we directly used standardized data as input, which could better reflect the superior performance of our proposed model.

In order to study the influence of the different number of hidden layers on the prediction performance, DNNs with two, three, four, five, six, seven (this paper) and eight hidden layers were tested. Other parameters remained at their default values during the test. The corresponding models were constructed for experiments, and RMSE and R² were selected to evaluate the model. The results are shown in Figure 8. It can be seen that the curve of the RMSE is in the shape of “V”. When the number of hidden layers was two, the maximum RMSE of the model was 0.2375, which then decreased with increases in the number of layers. However, there was an extreme point beyond which the prediction accuracy of the model decreased as the number of layers continued to increase. When there were seven hidden layers, the minimum RMSE of the network was 0.2368 and the maximum R² was 0.9439. The experimental results verify the superiority of the proposed DNN model in the PMSM stator winding temperature prediction performance.

In order to study the influence of the number of hidden nodes on the prediction performance, DNNs with 10, 12, 14 (this paper), 16, 18 and 20 nodes in each hidden layer are tested. Other parameters remained at their default values during the test. The results are shown in Figure 9. It can be seen that the network with 14 hidden layer nodes had the minimum RMSE of 0.2371 and the maximum R² of 0.9438. The experimental results verify the superiority of the proposed DNN model in prediction performance.

In order to study the influence of different activation functions on the prediction performance of the model, linear function, tanh function, sigmoid function and ReLU function (this paper) were selected as the activation functions of DNN models, and these models were tested. Other parameters remained at their default values during the test. Results are shown in

Table 1. Prediction performance of DNN models with different activation functions.

Activation Functions	RMSE	R2
linear	0.2625	0.9310
tanh	0.2375	0.9435
sigmoid	0.2394	0.9427
ReLU (this paper)	0.2369	0.9438

. The prediction accuracy of the DNN model using a ReLU function was the highest, with an RMSE of 0.2369 and an R² of 0.9438. The experimental results verify the superiority of the proposed DNN model in prediction performance.

In order to study the influence of the learning rate of the back propagation algorithm on the prediction performance of the DNN model, six different learning rates were used to establish the models for testing. Other parameters remained at their default values during the test. Since the difference of metrics were too small, six decimal places were reserved.

Table 2. Prediction performance of DNN models with different learning rates.

Learning Rates	Title 2	R2
0.0001	0.239620	0.942582
0.001 (this paper)	0.237080	0.943793
0.002	0.237114	0.943777
0.01	0.242495	0.941196
0.02	0.278323	0.922536
0.1	0.998120	0.003756

shows the results, when the learning rate was 0.001, with a minimum MSE of 0.237080 and a maximum R² of 0.943793. The experimental results verify the advantages of the proposed DNN model in PMSM stator winding temperature prediction.

In summary, the DNN model proposed in this paper was compared with DNN models with different numbers of hidden layers, different numbers of hidden layer nodes, different activation functions and different learning rates. The model proposed in this paper showed the best prediction performance in all experiments. In practical application, the DNN model proposed in this paper is the first choice for predicting PMSM stator winding temperature.

3.4. Comparison with Machine Learning Methods

In order to build a comparison with other models more fairly, instead of employed normalization and anti-normalization methods, we directly used standardized data as input, which can better reflect the superior performance of our proposed model.

In order to verify the effectiveness of the DNN model in PMSM stator winding temperature prediction, three traditional machine learning methods (i.e., support vector regression (SVR), decision tree and ridge regression), and two ensemble learning methods (i.e., random forest and AdaBoosting) were selected for comparative experiments. The original sample data were trained and verified 50 times for each experiment, and the average of the metrics was calculated. The results are shown in

Table 3. Comparison of metrics.

Methods	MAE 1	RMSE	R2
SVR 2	0.3996	0.5094	0.7405
DecisionTree	0.4516	0.5817	0.6616
Ridge	0.1731	0.2510	0.9370
RandomForest	0.4203	0.4937	0.7562
AdaBoosting	0.4354	0.4937	0.7563
DNN	0.1515	0.2368	0.9439

¹ mean absolute error. ² support vector regression.

.

The results show that, when predicting PMSM stator winding temperature, the DNN model proposed in this paper obtained the best performance. The MAE was 0.1515 and the RMSE was 0.2368, thus the prediction error of the model was the least. The R² is 0.9439, which was the closest to 1, and proves that the performance of the model fitting the real data was the best.

Figure 10 shows the results of three metrics of the models. It can be seen that the MAE and RMSE of the ridge regression model and the DNN model are smaller than those of other models, that the R² is larger, and that the prediction results of the DNN were better than ridge regression. Compared with the worst model (decision tree), the R² of the proposed model was improved by about 42%, and it also improved on the ridge regression model by 0.0069. The DNN model proposed in this paper can predict a PMSM stator winding temperature better than other models.

4. Conclusions and Prospections

In order to effectively predict PMSM stator winding temperature, a PMSM stator winding temperature prediction model based on a DNN was proposed in this paper. The model was trained and tested by partial data of a common sample set. Experiments on the number of hidden layers, the number of hidden layer nodes, different activation functions and different learning rates of the DNN models were carried out to verify the superiority of the DNN model proposed in this paper in prediction performance. Additionally, by calculating three metrics (i.e., MAE, RMSE and R²), the prediction performance of the proposed DNN model was compared with other machine learning methods. The summary of this paper is as follows:

• This paper presented a PMSM stator winding temperature prediction model based on a DNN. The model can be used to solve the problem of how to determine the temperature of PMSM stator winding. It can effectively prevent a series of faults of PMSM due to the high temperature of stator winding. It is of great significance to ensure the safe and reliable operation of the PMSM.
• The model proposed in this paper was compared with DNN models with different numbers of hidden layers, different numbers of hidden layer nodes, different activation functions and different learning rates, as well as with other machine learning methods. The results of directly inputting the dataset were as follows. The MAE of this model was 0.1515 and the RMSE was 0.2368, which is smaller than other models, while the R² was 0.9439, which is the closest to 1. The results of employing normalization and anti-normalization methods were also obtained. The MAE was 0.0151, the RMSE was 0.0214 and the R² was 0.9992. Therefore, this model is more suitable for PMSM stator winding temperature prediction under complex nonlinear conditions.

In conclusion, the DNN model proposed in this paper shows better performance than other machine learning methods in PMSM stator winding temperature prediction. The model can play an important role in PMSM temperature detection system, and provide technical support for temperature warning and the safe operation of PMSMs.

In the future, our next step is to find a lower-cost measurement method and verify the universality of the proposed model in the case of a different power of the same PMSM or different PMSMs. Moreover, we are also considering the construction of a larger sample set to conduct time series prediction for the features of PMSMs.