1. Introduction
Building performance simulation tools such as EnergyPlus [
1], TRNSYS [
2] etc., requires detailed information on the magnitudes of diffuse and direct components of solar radiation for prediction of energy consumption [
3]. The knowledge of these components also enables us to simulate light behavior in complicated environments and render High-dynamic-range (HDR) photorealistic images using lighting visualization tools such as Radiance [
4] that are invaluable for designers, architects and daylight simulation [
5] researchers alike. Sizing and configuration of solar energy systems such as solar thermal collectors and photovoltaic cells entail reliable solar radiation measurements. However, measuring both these components simultaneously can be expensive as measuring the direct component requires a pyrheliometer along with a solar tracker to track the sun at all times and similarly a shadow band with a pyranometer is needed for the diffuse component. Global solar radiation, which includes both these components, is rather simple and commonly measured not only in meteorological stations but also in smaller local weather stations. A cost-effective approach to obtain diffuse and direct components is to either use various correlations, or develop prediction models based on global solar radiation along with other meteorological parameters.
Several studies evaluating the diffuse component started to appear in the 1960s based on the work of Liu and Jordan [
6], which utilised curve fitting models with polynomial terms. Most of the models that are based on Liu and Jordan [
6], like Orgill and Hollands [
7], Erbs et al. [
8], Reindl et al. [
9] etc., are based on the relationship between the clearness index (
) and diffuse fraction (
), where
is the ratio between diffuse (
) and Global horizontal irradiance (
) and
is the ratio between Global horizontal irradiance (
) and extraterrestrial solar irradiance (
). Although they are based only on this relationship, their models differed as they developed them on different datasets. Therefore, these models are to be curve fitted frequently to adapt to the new datasets, which makes the generalization of these models very difficult.
Recent studies have shown that machine learning approaches have made promising strides in this field. Boland et al. [
10] and Ruiz-Arias et al. [
11] developed logistic and regression models respectively for diffuse fraction prediction. Soares et al. [
12] modeled a perceptron neural-network for São Paulo City, Brazil, to estimate hourly values of the diffuse solar-radiation, which perfomed better than the existing polynomial models. Similar studies conducted by Elminir et al. [
13] and Ihya et al. [
14] in Egypt and Morocco respectively also supports the fact that neural networks are better predictors than other linear regression models. A recent review by Berrizbeitia et al. [
15] also perfectly summarized both empirical and machine learning based models, but many of these models have not explored the possibility of the generalization of these models on different climates. In most of these models, the training data and testing data is from the same climates. Most of the regression models can show exceptional performance in this type of experimental setup, but they fail to show the same performance on different climates. Most of the climates do not have historical data to develop good regression models, but there might be some climates around it which may be abundant in such data. The idea of our research is to harvest this data to develop models and reliably use it to predict for climates that lack historical data.
This motivated us to explore the contemporary ways of exploiting the data using machine learning algorithms, as they learn to adapt and produce reliable and repeatable results. While experimenting with several models we also found that their performance is affected by their training datasets. Therefore, we bring forward to the readers our observations and present some recommendations to improve the generalizing capability of these models.
In
Section 2, we first give a brief introduction of all the predictive models compared in this study along with finetuning techniques that improve the performance of these models. The polynomial model of Erbs et al. is chosen as a baseline to compare against other machine learning models (linear regression, decision tree, random forests, gradient boosting and XGBoost, and an artificial neural network). The workflow of this study is to first find the best performing approaches by comparing them on the same datasets and then check for their generalizability on a third unseen dataset. Secondly, the best performing approaches are tested with completely different datasets to see if they can reliably make similar predictions and analyze what factors would affect their performance. To make the results reproducible all datasets used in this study along with their locations and data preprocessing techniques are mentioned in
Section 3.
Explored hyperparameter configurations of the machine learning models and thus achieved best configurations through finetuning are described in
Section 4. Here we also present our findings in two parts. First we present the performance of all the predictive models based on the most commonly used metrics for all the datasets considered in this study along with their generalization capability. Secondly we select the best performing approaches from the first part and train them with U.S. climates and tested them on European climate to check their reliability. Finally, for each part we discuss our findings and present our recommendations on how to select the training datasets to achieve better performing models.
4. Results and Discussion
4.1. Tuning Results
Prior to the test for generalizability, the models are finetuned to give improved validation performance. Grid search is performed on the machine learning models based on several hyperparameters. Decision trees, random forests, gradient boosting trees, and XGBoost trees are each grid searched at several depths starting from 4 until 15. Random forests are tested with several different numbers of trees starting from 50 until 250. When it comes to boosting stages of gradient boosting and XGBoost, they are also grid-searched starting from 50 until 250 stages. Additionally, a few hyperparameters are searched in XGBoost models such as the learning rate (from 0.05 to 0.15), subsample ratio (from 0.08 to 0.1 ) and L2 regularization [
37] of weights (from 0.80 to 1). The hyperparameters for the machine learning models can be seen in
Table 5.
The neural networks chosen in this study for both parts are similar. They are feed forward MLPs and have 11 features (Mannheim and Ensheim) and 10 features (U.S), 6 hidden layers (shown in
Table 6) and the output with a single neuron gives diffuse fraction (
) with sigmoid as the activation function. All hidden layers except the last hidden layer have the dropout regularization added. The dropout fraction is set to 0.3.
Neural networks are implemented using Keras library [
38] and Grid search from Scikit learn [
26] is implemented to search for the best combination of hyperparameters.
The choice of activation functions for all the hidden layers are ELU (Exponential Linear unit) [
39], sigmoid [
40] and tanh. Early stopping is implemented with validation loss as a proxy to stop training automatically after 10 epochs in the case of no improvement. A model checkpoint is implemented to save the best models at every epoch. The loss function used is mean square error and the optimizer ‘Adam’ [
41] is chosen, as it has shown some good results with the default configuration of learning parameters.
Table 6 shows the combination of activations functions obtained by grid search for hidden layers in Ensheim, Mannheim and U.S. models.
4.2. First Study
Before the predictive models are trained, a small analysis of the data is performed to see how the input features influence the output, i.e., diffuse fraction. Mutual information(MI) [
42] and the R
2 correlation [
43] of the input features with respect to the output
is used for this analysis.
Figure 1 ascertains the significance of each input feature.
MI is a measure of mutual dependence between the variables, whereas R2 correlation gives a proportion of variance that the independent variable predicts from a dependent variable. It can be observed that diffuse fraction is primarily dependent on global horizontal irradiance and the clearness index, but the other parameters also show considerable but varying influences in both climates.
Since the machine learning models can easily handle these minimal number of input features, we considered all the features without discrimination for machine learning models. Unlike the machine learning models, the polynomial models depend mostly on a few significant predictors so input features are considered according to their requirements.
For machine learning models the following features are considered: day of the year (d), hour (h), solar altitude () (considering site elevation, and ), clearness index (), global horizontal irradiance (), atmospheric pressure (), air temperature (), relative humidity (), wind speed (), wind direction (). and are calculated according to Equations (4) and (5).
Two sets of predictive models are developed each for Mannheim and Ensheim climates. All the machine learning models in this part are trained on 2013-2016 data and validated on 2017 data for each of the datasets.
Table 7 and
Table 8 shows the comparison of the performances of each predictive model on training and validation datasets for Mannheim and Ensheim climates.
The predictive models are abbreviated as NN (neural network), XGB (XGBoosting), GB (gradient boosting), RF (random forests), DT (decision trees) and LR (linear regression). The configuration of all the machine learning models can be seen in
Table 5 and for neural networks in
Table 6. The coefficients for the Erbs et al. model can be seen in
Table 1. All the models output diffuse fraction, from which diffuse horizontal irradiance is calculated using Equation (
11).
The results in
Table 7 show that NN, XGB, GB and RF showed good performance with 26–27% of nRMSE for Mannheim. They showed equally good performance with respect to other metrics as well. In comparision NN fared well, while the other three models showed similar performance. Linear regression and Erbs et al. model showed least performance compared to others. A similar trend can be seen on Ensheim climate by the predictive models (see
Table 8). Interestingly the nRMSE has differed between the climates by about 3–4% for all the models but the other three metrics remain the same. In summary neural network (NN) showed best performance on both climates with RMSE of 39 W/m
2 and MAE of 22 W/m
2.
4.3. Test for Generalizability
A third climate, Weinbiet, which has measured diffuse irradiance values, is selected to test for generalizabilty. The Weinbiet weather station (as shown in
Figure 2) is located between Mannheim and Ensheim but is considerably closer to the Mannheim weather station (30 KM) rather than Ensheim (75 KM).
The Weinbiet dataset is preprocessed similarly to the Ensheim and Mannheim datasets. The true diffuse fraction values from the Weinbiet dataset are only used to measure the predictive performance of the models on the Weinbiet dataset.
Testing the above models on the Weinbiet data shows that the models that are trained on Mannheim showed better performance than on the Ensheim dataset, which is clearly evident from
Table 9. Once again NN, XGB, GB and RF showed similar nRMSE of 27% (on Mannheim) but their nMBE’s differed significantly. In this case NN showed least nMBE of just 0.33% thus faring better than other predictive models. It can also be observed that the neural network performance on its original dataset of Mannheim (see
Table 7) and unseen dataset of Weinbiet are almost similar in nRMSE of 26% and 27% respectively. Though the other models generalized similarly to NN, their nMBE increased significantly on the unseen dataset, which makes their predictions less stable due to high variation. On the other hand models trained on Ensheim seems even less reliable due to high nMBE at around −7 to −8%. These results show that models trained on Mannheim are more favorable for predictions with respect to Weinbiet.
A closer look is taken into all the three datasets in order to better understand this phenomenon.
Figure 2 shows the correlation of the Weinbiet dataset with the Ensheim and Mannheim datasets. The bar plots show the correlation of each input feature from Mannheim and Ensheim datasets with respect to the Weinbiet dataset. The bar plots for input features corresponding to Mannheim show better correlation when compared to that of Ensheim, which means that the Weinbiet model is more similar to the Mannheim dataset than the Ensheim dataset. This explains that models trained on Mannheim perform better than that of Ensheim.
These results suggest that a pre-trained machine learning model, provided the training dataset is chosen carefully, can make really good predictions on unseen data.
4.4. Second Study
From the first part we concluded that NN performed well among other models, but we would like to ascertain if such reliable predictions can be made on a global scale (at least on two different continents). Apart from NN, XGB is one other approach that consistently performed comparable to NN. So in this part, two approaches namely NN and XGB are used to train the models.
The training data is a consolidated data of seven U.S. climates collected from the SURFRAD network (see
Table 3) from the year 2015. Both NN and XGB models are finetuned and then validated against 2016 data. To test these models, 2016 data from four European climates (France, Spain and The Netherlands) are considered (see
Table 4). Due to unavailability, wind direction and wind speed are not considered, instead satellite-based diffuse fraction (from CAMS-RAD), which is available at most places in the U.S. (NSRDB) and Europe (BSRN) is considered.
Individual models with respect to each of the seven U.S. climates are also developed to compare against the main model, i.e., the model based on the consolidated data of all the seven climates. This gives us a better picture of how good or bad the combined model performs with respect to each climate individually. For instance, the nRMSE of individual models (NN) are in the range of 25 to 31%, whereas the performance of the combined model is 27% (see
Table 10). This confirms that the combined model appropriately represents all the underlying climates without much disparity. While comparing the performances of NN and XGB models, it can be seen that in almost all the climates once again NN models have performed better.
4.5. Test for Generalizability
Four climates in Europe (two in France, one each in The Netherlands and Spain) are selected to test the generalizability of models that are trained on U.S. data. The bottom part of
Table 10 shows the performance metrics.
The performance of NN and XGB are almost similar on European climates in most of the metrics. The nRMSE of the U.S. trained model on European datasets is between 23 to 29% and on its original dataset is 27%. This performance is even better than those of individual models performed on their original datasets (25 to 31%). This shows that these models have shown very good generalizability, in fact even better than their original performance in some cases. This performance gain can be attributed to the fact that the model trained on the consolidated dataset has seen more patterns than individual datasets.
From the above results, it is shown that the right choice of training data can improve the predictive performance of these models.
A cross comparison of the predictive models from both the studies shows a more interesting result.
Table 11 shows the performance of all the three NNs on the dataset of Weinbiet. It can be observed that the model trained based on the Mannheim dataset performs better than Ensheim dataset or a combination of U.S. datasets. The nRMSE of NN (Mannheim) is 27% whereas the NN (Ensheim) and NN (U.S) achieved around 29%. Though the model trained on the consolidated dataset of U.S. climates learned more weather patterns, its performance is overshadowed by the NN (Mannheim), which was trained on local data. Since Mannheim data correlates well with Weinbiet (see
Figure 2), here NN (Mannheim) has the advantage.
Neverthless the performance of NN models (Ensheim and the U.S.) does not deviate too much from that of Mannheim. Therefore, the following conclusions can be made about choosing the training data:
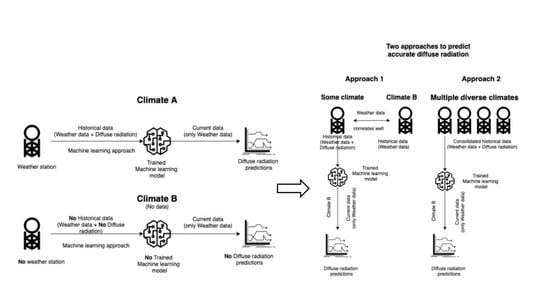
When the predictions are to be done on a microclimate level with high precision, choosing a local training dataset with a good correlation to the test dataset would be a better choice.
To make predictions for a variety of climates, a generic model trained on a combination of different climate datasets, does an excellent job.
Since the general availability of the measured data of diffuse irradiance is scarce, this approach of using a pre-trained model along with generally available data from local weather stations gives easy access to accurate diffuse irradiance data.
5. Conclusions
The main goal of this article was to test the generalization capability of the hourly diffuse horizontal irradiance prediction models and also to understand the factors that can improve their performance. The experiments in this study were divided into two parts.
In the first part, seven predictive approaches (six machine learning and one polynomial) were each trained on two German climates (Mannheim and Ensheim). They were first finetuned and validated on their respective climates before they were tested on a third German climate (Weinbiet). We observed that among all the considered approaches, neural networks and XGBoost have exhibited good generalization capabilities when compared to others. Neural networks consistently performed with low mean absolute error (MAE) of 22 W/m2 on validation datasets of both the climates (Mannheim and Ensheim). While testing on a third climate (Weinbiet), it is observed that the neural network model trained on Mannheim (24 W/m2) performed better than that of Ensheim (28 W/m2). This was a bit surprising as both climates (Mannheim and Ensheim) are close to the third climate (Weinbiet). A quick look into the datasets of all three climates revealed that the Weinbeit dataset (test set) correlates better with Mannheim than Ensheim, which explains the reason behind a better performance of the model, for example, trained on the Mannheim dataset. Though the neural network performed better in all the tests at the local level (German climates), we would like to confirm if it can reliably make good predictions on a global level. Therefore, we shortlisted neural networks and the XGBoost model for our next part to test on more climates.
In the second part, the data was taken from seven different climates in the U.S. and is consolidated and then used to train neural networks and XGBoost models. These models are then tested on four European climates (two from France, one each from The Netherlands and Spain). Once again Neural networks did a great job with MAE of 23 W/m2 on its validation set and generalized well on European climates with MAE in the range 20–27 W/m2. Individual models for each of the U.S. climates are also developed for a comparison. These models also achieved MAE in the range of 20–26 W/m2. This indicates that the developed neural networks showed their original performance even on unseen European datasets. Such generalization capability is seldom achieved but in this case it is possible because the model is trained on a consolidated training set. This contributed the model to learn varied weather patterns from seven different U.S. climates and make good predictions on European climates.
Both studies conclude that neural networks are excellent predictors and careful selection of training data can improve their performance considerably. Neural networks seem like a black box model due to the complex relationships between neurons, but they showed better predictions than their counterparts. In this regard, XGBoost fared surprisingly close to neural networks. Considering the time required to train and validate a neural network model, an XGB model did an excellent job with performance on par with neural networks.
This research has several practical applications especially for the simulation tools that need diffuse and direct components of the solar radiation. Researchers who use standard weather files in their simulations, can benefit from these trained models by incorporating directly into their tools.