Chattering Free Adaptive Sliding Mode Controller for Photovoltaic Panels with Maximum Power Point Tracking †
Abstract
:1. Introduction
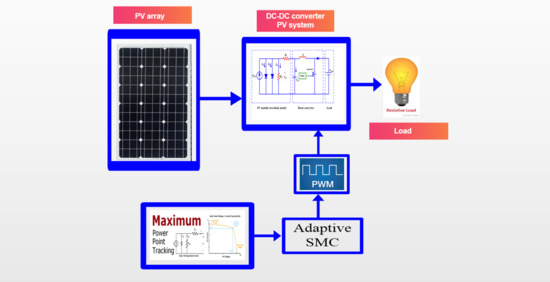
2. Problem Formulation
3. System Model
3.1. MPPT Algorithms
3.1.1. MPPT Algorithm Based on P&O
3.1.2. MPPT Algorithm Based on PSO
3.1.3. MPPT Algorithm Based on IPSM
3.2. Control Scheme
Control Law
4. Simulation Results and Discussion
4.1. Simulation Results
4.1.1. Response Using P&O
4.1.2. Response Using PSO
4.1.3. Response Using Improved PSM
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ekins, P.; Bradshaw, M.J.; Watson, J. Global Energy: Issues, Potentials, and Policy Implications; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Ram, J.P.; Babu, T.S.; Rajasekar, N. A comprehensive review on solar PV maximum power point tracking techniques. Renew. Sustain. Energy Rev. 2017, 67, 826–847. [Google Scholar] [CrossRef]
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Elbaset, A.A.; Khaled, M.; Ali, H.; Sattar, M.A.-E. Implementation of a modified perturb and observe maximum power point tracking algorithm for photovoltaic system using an embedded microcontroller. IET Renew. Power Gener. 2016, 10, 551–560. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. Modified Incremental Conductance Algorithm for Photovoltaic System Under Partial Shading Conditions and Load Variation. IEEE Trans. Ind. Electron. 2014, 61, 5384–5392. [Google Scholar] [CrossRef]
- Titri, S.; Larbes, C.; Toumi, K.Y.; Benatchba, K. A new MPPT controller based on the Ant colony optimization algorithm for Photovoltaic systems under partial shading conditions. Appl. Soft Comput. J. 2017, 58, 465–479. [Google Scholar] [CrossRef]
- Ali, A.; Almutairi, K.; Malik, M.Z.; Irshad, K.; Tirth, V.; Algarni, S.; Zahir, H.; Islam, S.; Shafiullah, M.; Shukla, N.K. Review of Online and Soft Computing Maximum Power Point Tracking Techniques under Non-Uniform Solar Irradiation Conditions. Energies 2020, 13, 3256. [Google Scholar] [CrossRef]
- Bahgat, A.; Helwa, N.; Ahmad, G.; El Shenawy, E. Maximum power point traking controller for PV systems using neural networks. Renew. Energy 2005, 30, 1257–1268. [Google Scholar] [CrossRef]
- Sampaio, L.P.; Da Rocha, M.V.; Da Silva, S.A.O.; De Freitas, M.H.T.; De Freitas, M.T. Comparative analysis of MPPT algorithms bio-inspired by grey wolves employing a feed-forward control loop in a three-phase grid-connected photovoltaic system. IET Renew. Power Gener. 2019, 13, 1379–1390. [Google Scholar] [CrossRef]
- Purnama, I.; Lo, Y.-K.; Chiu, H.-J. A Fuzzy Control Maximum Power Point Tracking Photovoltaic System, Proceedings of the 2011 IEEE International Conference on Fuzzy Systems, Taipei, Taiwan, 27–30 June 2011; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2011; pp. 2432–2439. [Google Scholar]
- Elobaid, L.M.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial neural network-based photovoltaic maximum power point tracking techniques: A survey. IET Renew. Power Gener. 2015, 9, 1043–1063. [Google Scholar] [CrossRef]
- Kulaksız, A.A.; Akkaya, R. A genetic algorithm optimized ANN-based MPPT algorithm for a stand-alone PV system with induction motor drive. Sol. Energy 2012, 86, 2366–2375. [Google Scholar] [CrossRef]
- Ferdiansyah, I.; Sutedjo, S.; Qudsi, O.A.; Ramadhan, A.N. Implementation of Maximum Power Point Tracking on Solar Panels using Cuckoo Search Algorithm Method. In Proceedings of the 2nd International Conference on Applied Information Technology and Innovation, Denpasar, Bali, 21–22 September 2019; pp. 88–92. [Google Scholar] [CrossRef]
- Besheer, A.H.; Adly, M. Ant Colony System Based Pi Maximum Power Point Tracking for Stand Alone Photovoltaic System. In Proceedings of the 2012 IEEE International Conference on Industrial Technology, Athens, Greece, 19–21 March 2012; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2012; pp. 693–698. [Google Scholar]
- Renaudineau, H.; Donatantonio, F.; Fontchastagner, J.; Petrone, G.; Spagnuolo, G.; Martin, J.-P.; Pierfederici, S. A PSO-Based Global MPPT Technique for Distributed PV Power Generation. IEEE Trans. Ind. Electron. 2014, 62, 1047–1058. [Google Scholar] [CrossRef]
- Tajuddin, M.F.N.; Ayob, S.M.; Salam, Z.; Saad, M.S. Evolutionary based maximum power point tracking technique using differential evolution algorithm. Energy Build. 2013, 67, 245–252. [Google Scholar] [CrossRef]
- Javed, M.Y.; Murtaza, A.F.; Ling, Q.; Qamar, S.; Gulzar, M.M.; Javed, Y. A novel MPPT design using generalized pattern search for partial shading. Energy Build. 2016, 133, 59–69. [Google Scholar] [CrossRef]
- Audet, C. Convergence Results for Generalized Pattern Search Algorithms are Tight. Optim. Eng. 2004, 5, 101–122. [Google Scholar] [CrossRef] [Green Version]
- Veerapen, S.; Wen, H.; Du, Y. Design of a novel MPPT algorithm based on the two stage searching method for PV systems under partial shading. In Proceedings of the 3rd International Future Energy Electronics Conference and ECCE Asia, Kaohsiung, Taiwan, 3–7 June 2017; pp. 1494–1498. [Google Scholar] [CrossRef]
- Abdelrassoul, R.; Ali, Y.; Zaghloul, M.S. Genetic Algorithm-Optimized PID Controller for Better Performance of PV System. In Proceedings of the 2016 World Symposium on Computer Applications and Research, Cairo, Egypt, 12–14 March 2016; pp. 18–22. [Google Scholar]
- Ali, A.I.M.; Mohamed, E.E.M.; Youssef, A.R. MPPT algorithm for grid-connected photovoltaic generation systems via model predictive controller. In Proceedings of the 19th International Middle-East Power Systems Conference, Cairo, Egypt, 19–21 December 2018; pp. 895–900. [Google Scholar]
- Guler, N.; Irmak, E. MPPT based model predictive control of grid connected inverter for PV system. In Proceedings of the 8th International Conference of Renewable. Energy Research and Applications, Brasov Romania, 3–6 November 2019; pp. 982–986. [Google Scholar]
- Khanna, R.; Zhang, Q.; Stanchina, W.E.; Reed, G.F.; Mao, Z.-H. Maximum Power Point Tracking Using Model Reference Adaptive Control. IEEE Trans. Power Electron. 2013, 29, 1490–1499. [Google Scholar] [CrossRef]
- Chavarria, J.; Biel, D.; Guinjoan, F.; Meza, C.; Negroni, J.J. Energy-Balance Control of PV Cascaded Multilevel Grid-Connected Inverters Under Level-Shifted and Phase-Shifted PWMs. IEEE Trans. Ind. Electron. 2012, 60, 98–111. [Google Scholar] [CrossRef]
- Iftikhar, R.; Ahmad, I.; Arsalan, M.; Naz, N.; Ali, N.; Armghan, H. MPPT for Photovoltaic System Using Nonlinear Controller. Int. J. Photoenergy 2018, 2018, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Chaibi, Y.; Salhi, M.; El-Jouni, A. Sliding mode controllers for standalone PV systems: Modeling and approach of control. Int. J. Photoenergy 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, F.F.; Ghenai, C.; Hamid, A.K.; Bettayeb, M. Application of sliding mode control for maximum power point tracking of solar photovoltaic systems: A comprehensive review. Annu. Rev. Control. 2020, 49, 173–196. [Google Scholar] [CrossRef]
- Bianconi, E.; Calvente, J.; Giral, R.; Petrone, G.; Paja, C.A.R.; Spagnuolo, G.; Vitelli, M. A Fast Current-Based Mppt Technique Based on Sliding Mode Control. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 59–64. [Google Scholar] [CrossRef]
- Chu, C.-C.; Chen, C.-L. Robust maximum power point tracking method for photovoltaic cells: A sliding mode control approach. Sol. Energy 2009, 83, 1370–1378. [Google Scholar] [CrossRef]
- Kchaou, A.; Naamane, A.; Koubaa, Y.; M’Sirdi, N. Second order sliding mode-based MPPT control for photovoltaic applications. Sol. Energy 2017, 155, 758–769. [Google Scholar] [CrossRef]
- Mojallizadeh, M.R.; Badamchizadeh, M.; Khanmohammadi, S.; Sabahi, M. Designing a new robust sliding mode controller for maximum power point tracking of photovoltaic cells. Sol. Energy 2016, 132, 538–546. [Google Scholar] [CrossRef]
- Kchaou, A.; Ayadi, A.; Naamane, A.; M’Sirdi, N.; Koubaa, Y. An Adaptive Sliding Mode Control based Maximum power point tracking method for a PV stand-alone system. In Proceedings of the 6th International Conference on Systems and Control, Batna, Algeria, 7–9 May 2017; pp. 69–74. [Google Scholar]
- Ali, H.G.; Vilanova, R.; Pelez-Restrepo, J. Perturb & Observe based Adaptive Sliding Mode MPPT Control of Solar Photovoltaic System. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering, Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Ali, H.G.; Vilanova, R.; Herrera, J.; Tobón, A.; Peláez-Restrepo, J. Non-Linear Sliding Mode Controller for Photovoltaic Panels with Maximum Power Point Tracking. Process 2020, 8, 108. [Google Scholar] [CrossRef] [Green Version]
- Babu, T.S.; Ram, J.P.; Sangeetha, K.; Laudani, A.; Rajasekar, N. Parameter extraction of two diode solar PV model using Fireworks algorithm. Sol. Energy 2016, 140, 265–276. [Google Scholar] [CrossRef]
- Hina; Noor, A.; Abbas, M.; Karimov, K.S. Non-inductive DC-DC regulated boost converter as battery charger for photovoltaic installation. In Proceedings of the 2015 Power Generation System and Renewable Energy Technologies, Islamabad, Pakistan, 10–11 June 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Salam, Z.; Ahmed, J.; Merugu, B.S. The application of soft computing methods for MPPT of PV system: A technological and status review. Appl. Energy 2013, 107, 135–148. [Google Scholar] [CrossRef]
- Soon, J.J.; Low, K.-S. Photovoltaic Model Identification Using Particle Swarm Optimization With Inverse Barrier Constraint. IEEE Trans. Power Electron. 2012, 27, 3975–3983. [Google Scholar] [CrossRef]
- Koessler, E.; Almomani, A. Hybrid particle swarm optimization and pattern search algorithm. Optim. Eng. 2020, 1–17. [Google Scholar] [CrossRef]
- PSIM Tutorial: How to Use Solar Module Physical Model. Available online: https://powersimtech.com/drive/uploads/2016/04/Tutorial-Solar-Module-physical-model.pdf (accessed on 1 April 2016).











| Symbol | Parameter | Value |
|---|---|---|
| ISC | Short-circuit current | 3.8 A |
| VOC | Open-circuit voltage | 21.1 V |
| Imp | Maximum panel current | 3.5 A |
| VPV | Maximum panel voltage | 17.1 V |
| IS1= IS2 | Saturation currents | 4.704 × 10−10 |
| IPV | Panel current | 3.8 A |
| Rsh | Shunt resistance | 176.4 Ω |
| Rs | Series resistance | 0.35 Ω. |
| Parameters | Value |
|---|---|
| L | 22 µF |
| C | 100 µF |
| Vo | 24 V |
| fsw0 (controller) | 49.2 kHz |
| KP | 0.1 |
| KI | 50 |
| Kd | 0.1 |
| K1 | 4.3 |
| KA | 55.5 |
| Ta | 400 µs |
| ΔVo ΔVo ΔVo | 1 V (P&O) 0.2 V (40 p.) 0.8 V (10 p.) |
| LPF | 20 kHz |
| Controller | Over/Undershoot (%) | Settling Time (Second) | Power Losses (Watt) |
|---|---|---|---|
| PID | 2.8 | 5.3 ms | 3.2 |
| ASMC | 0.6 | 0.15 ms | 0.68 |
| Controller | Over/Undershoot (%) | Settling Time (Second) | Power Losses (Watt) |
|---|---|---|---|
| PID | 8 | 80 ms | 6 |
| ASMC | 0.85 | 2.8 ms | 0.95 |
| Controller | Over/Undershoot (%) | Settling Time (Second) | Power Losses (Watt) |
|---|---|---|---|
| PID | 10 | 120 ms | 7.8 |
| ASMC | 1 | 3 ms | 1.2 |
| Controller | Over/Undershoot (%) | Settling Time (Second) | Power Losses (Watt) |
|---|---|---|---|
| PID | 5 | 50 ms | 4.8 |
| ASMC | 0.40 | 0.10 ms | 0.54 |
| Controller | Over/Undershoot (%) | Settling Time (Second) | Power Losses (Watt) |
|---|---|---|---|
| PID | 5.8 | 53 ms | 5.2 |
| ASMC | 0.41 | 0.11 ms | 0.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gohar Ali, H.; Arbos, R.V. Chattering Free Adaptive Sliding Mode Controller for Photovoltaic Panels with Maximum Power Point Tracking. Energies 2020, 13, 5678. https://doi.org/10.3390/en13215678
Gohar Ali H, Arbos RV. Chattering Free Adaptive Sliding Mode Controller for Photovoltaic Panels with Maximum Power Point Tracking. Energies. 2020; 13(21):5678. https://doi.org/10.3390/en13215678
Chicago/Turabian StyleGohar Ali, Hina, and Ramon Vilanova Arbos. 2020. "Chattering Free Adaptive Sliding Mode Controller for Photovoltaic Panels with Maximum Power Point Tracking" Energies 13, no. 21: 5678. https://doi.org/10.3390/en13215678
APA StyleGohar Ali, H., & Arbos, R. V. (2020). Chattering Free Adaptive Sliding Mode Controller for Photovoltaic Panels with Maximum Power Point Tracking. Energies, 13(21), 5678. https://doi.org/10.3390/en13215678