Effect of Phase Change Material Storage on the Dynamic Performance of a Direct Vapor Generation Solar Organic Rankine Cycle System
Abstract
:1. Introduction
- A PCM storage tank model development and its validation using the finite difference method in the MATLAB programming environment.
- The dynamic simulation of a PCM-coupled DVG solar ORC storage system on a weekly, monthly, and annual basis.
- The evaluation of the fall in working fluid temperatures and rise in PCM temperatures and the quantity of energy stored and released by the PCM during the charging and discharging process.
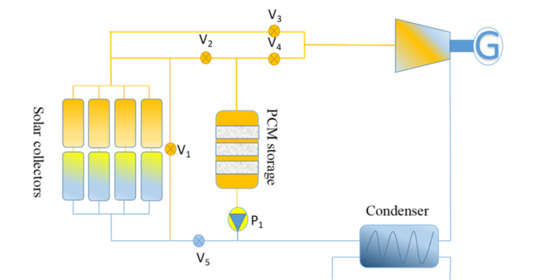
2. System Description and Control
- If the melting point temperature of the PCM was kept lower than the evaporation temperature of the working fluid, then the system lay in charging mode (Tevp > Tm).
- If the melting point temperature of the PCM was kept higher than the evaporation temperature of the working fluid, then the system lay in discharging mode (Tevp < Tm).
3. Thermodynamic Modeling
3.1. The Solar Radiation Collection System
3.2. Heat Storage System
- It was assumed that conduction was the major method of heat transfer within the PCM.
- The current study only considered one-dimensional heat transfer.
- It was also assumed that the thermo-physical properties of the PCM remained constant during each phase.
- Natural convection that can happen due to density differences was neglected in the present model.
3.3. Validation of the Current Model of the PCM
3.4. The Basic Organic Rankine Cycle
4. Results and Discussion
4.1. The Dynamic Performance of the PCM-Based DVG Solar ORC System During the Hottest Week
4.1.1. Variation in the Phase Change Material Temperature and Solar Radiation with Time
4.1.2. Variation in the Collector and ORC Efficiencies with Time
4.2. The Performance of the PCM-Based DVG Solar ORC System During the Whole Year
4.2.1. The Change in the ORC and Collector Efficiencies
4.2.2. The Changes in the System Efficiency and Net Power Output
4.2.3. The Change in the Quantity of Energy Stored by the PCM
4.2.4. The Fall in the Working Fluid Temperature and the Rise in the PCM Temperature
4.3. The Performance Enhancement in the DVG Solar ORC System by Employing the PCM Storage
4.3.1. The Rise in the ORC and System Efficiencies by Employing the PCM Storage
4.3.2. The Rise in the Net Power Output by Employing the PCM Storage
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | |
| A | Primary heat loss coefficient of the collector |
| B | Secondary heat loss coefficient of the collector |
| C | Heat capacity (kJ/kg·K) |
| G | Solar irradiance (W/m2) |
| H | Volumetric enthalpy of the PCM (kJ/m3) |
| h | Specific enthalpy (kJ/kg) |
| M | Mass of the PCM (kg) |
| m | Mass flow rate (kg/s) |
| Q | Quantity of heat (kJ) |
| q | Specific heat (kJ/kg) |
| S | Surface area of the collector (m2) |
| T | Temperature of the collector (°C) |
| w | Specific work (kJ/kg) |
| Greek Symbols | |
| Heat capacity coefficient, (J/°C) | |
| Mechanical efficiency | |
| Thermal efficiency | |
| Density, (kg/m3) | |
| Partial change | |
| Thermal conductivity, (W/m·K) | |
| Arithmetic solution, (°C) | |
| Latent heat of the PCM, (J) | |
| Abbreviations | |
| G | Generator |
| P | Pump |
| V | Valve |
| DVG | Direct vapor generation |
| EFPC | Evacuated flat plate collector |
| HTF | Heat transfer fluid |
| ORC | Organic Rankine cycle |
| LTS | Latent heat thermal storages |
| STS | Sensible thermal storage |
| PCM | Phase change material |
| TMY | Typical meteorological year |
| Subscripts/Superscript | |
| amb | Ambient |
| b | Binary |
| c | Critical |
| cl | Collector |
| cond | Condensation |
| e | Expander |
| evp | Evaporation |
| f | Fluid |
| g | Generator |
| i | Inlet |
| l | Liquid |
| o | Outlet |
| 0 | Reference state |
| os | Ideal state |
| m | Melting point |
| mx | Maximum |
| min | Minimum |
| ORC | Organic Rankine cycle |
| p | Power |
| PCM | Phase change material |
| sys | System |
| st | Stored |
| t | Turbine |
| rel | Released |
References
- Pina, E.A.; Serra, L.M.; Lozano, M.A.; Hernández, A.; Lázaro, A. Comparative Analysis and Design of a Solar-Based Parabolic Trough-ORC Cogeneration Plant for a Commercial Center. Energies 2020, 13, 4807. [Google Scholar] [CrossRef]
- Renno, C.; Petito, F.; D’Agostino, D.; Minichiello, F. Modeling of a CPV/T-ORC combined system adopted for an industrial user. Energies 2020, 13, 3476. [Google Scholar] [CrossRef]
- Ghaebi, H.; Rostamzadeh, H. Performance comparison of two new cogeneration systems for freshwater and power production based on organic Rankine and Kalina cycles driven by salinity-gradient solar pond. Renew. Energy 2020, 156, 748–767. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Rana, S.; Ahmadi, M.; Date, A.; Akbarzadeh, A. Experimental study on the prospect of low-temperature heat to power generation using Trilateral Flash Cycle (TFC). Appl. Therm. Eng. 2020, 172, 115139. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Khosravanifard, Y.; Sohani, A. Solutions for thermal energy exploitation from the exhaust of an industrial gas turbine using optimized bottoming cycles. Energy Convers. Manag. 2020, 207, 112523. [Google Scholar] [CrossRef]
- Li, J.; Alvi, J.Z.; Pei, G.; Su, Y.; Li, P.; Gao, G.; Ji, J. Modelling of organic Rankine cycle efficiency with respect to the equivalent hot side temperature. Energy 2016, 115, 668–683. [Google Scholar] [CrossRef] [Green Version]
- Usman, M.; Imran, M.; Yang, Y.; Lee, D.H.; Park, B.S. Thermo-economic comparison of air-cooled and cooling tower based Organic Rankine Cycle (ORC) with R245fa and R1233zde as candidate working fluids for different geographical climate conditions. Energy 2017, 123, 353–366. [Google Scholar] [CrossRef]
- Oyekale, J.; Petrollese, M.; Cau, G. Multi-objective thermo-economic optimization of biomass retrofit for an existing solar organic Rankine cycle power plant based on NSGA-II. Energy Rep. 2020, 6, 136–145. [Google Scholar] [CrossRef]
- Refiei, A.; Loni, R.; Najafi, G.; Sahin, A.Z.; Bellos, E. Effect of use of MWCNT/oil nanofluid on the performance of solar organic Rankine cycle. Energy Rep. 2020, 6, 782–794. [Google Scholar] [CrossRef]
- Xu, G.; Song, G.; Zhu, X.; Gao, W.; Li, H.; Quan, Y. Performance evaluation of a direct vapor generation supercritical ORC system driven by linear Fresnel reflector solar concentrator. Appl. Therm. Eng. 2015, 80, 196–204. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhao, L.; Wang, J.L. Experimental investigation on the low-temperature solar Rankine cycle system using R245fa. Energy Convers. Manag. 2011, 52, 946–952. [Google Scholar] [CrossRef]
- Wang, J.L.; Zhao, L.; Wang, X.D. An experimental study on the recuperative low temperature solar Rankine cycle using R245fa. Appl. Energy 2012, 94, 34–40. [Google Scholar] [CrossRef]
- Li, J.; Alvi, J.Z.; Pei, G.; Ji, J.; Li, P.; Fu, H. Effect of working fluids on the performance of a novel direct vapor generation solar organic Rankine cycle system. Appl. Therm. Eng. 2016, 98, 786–797. [Google Scholar] [CrossRef] [Green Version]
- Bu, X.B.; Li, H.S.; Wang, L.B. Performance analysis and working fluids selection of solar powered organic Rankine-vapor compression ice maker. Sol. Energy 2013, 95, 271–278. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhao, L.; Wang, J.L.; Zhang, W.Z.; Zhao, X.Z.; Wu, W. Performance evaluation of a low-temperature solar Rankine cycle system utilizing R245fa. Sol. Energy 2010, 84, 353–364. [Google Scholar] [CrossRef]
- Quoilin, S.; Orosz, M.; Hemond, H.; Lemort, V. Performance and design optimization of a low-cost solar organic Rankine cycle for remote power generation. Sol. Energy 2011, 85, 955–966. [Google Scholar] [CrossRef] [Green Version]
- Marion, M.; Voicu, I.; Tiffonnet, A.L. Wind effect on the performance of a solar organic Rankine cycle. Renew. Energy 2014, 68, 651–661. [Google Scholar] [CrossRef]
- Gang, P.; Jing, L.; Jie, J. Design and analysis of a novel low-temperature solar thermal electric system with two-stage collectors and heat storage units. Renew. Energy 2011, 36, 2324–2333. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Pei, G.; Ji, J.; Alvi, J.Z.; Xia, L. A Novel Hybrid Solar Power Generation System Using a-Si Photovoltaic/Thermal Collectors and Organic Rankine Cycle. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015; pp. 1–10. [Google Scholar]
- Tian, Y.; Zhao, C.Y. A review of solar collectors and thermal energy storage in solar thermal applications. Appl. Energy 2013, 104, 538–553. [Google Scholar] [CrossRef] [Green Version]
- Calise, F.; D’Accadia, M.D.; Vicidomini, M.; Scarpellino, M. Design and simulation of a prototype of a small-scale solar CHP system based on evacuated flat-plate solar collectors and Organic Rankine Cycle. Energy Convers. Manag. 2015, 90, 347–363. [Google Scholar] [CrossRef]
- Alvi, J.Z.; Imran, M.; Pei, G.; Li, J.; Gao, G.; Alvi, J. Thermodynamic comparison and dynamic simulation of direct and indirect solar organic Rankine cycle systems with PCM storage. Energy Procedia 2017, 129, 716–723. [Google Scholar] [CrossRef]
- Cinocca, A.; di Bartolomeo, M.; Cipollone, R.; Carapellucci, R. A Definitive Model of a Small-Scale Concentrated Solar Power Hybrid Plant Using Air as Heat Transfer Fluid with a Thermal Storage Section and ORC Plants for Energy Recovery. Energies 2020, 13, 4741. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Hasnain, S.M. Review on sustainable thermal energy storage technologies, Part I: Heat storage materials and techniques. Energy Convers. Manag. 1998, 39, 1127–1138. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Manfrida, G.; Secchi, R.; Stańczyk, K. Modelling and simulation of phase change material latent heat storages applied to a solar-powered Organic Rankine Cycle. Appl. Energy 2016, 179, 378–388. [Google Scholar] [CrossRef] [Green Version]
- Lakhani, S.; Raul, A.; Saha, S.K. Dynamic modelling of ORC-based solar thermal power plant integrated with multitube shell and tube latent heat thermal storage system. Appl. Therm. Eng. 2017, 123, 458–470. [Google Scholar] [CrossRef]
- Freeman, J.; Guarracino, I.; Kalogirou, S.A.; Markides, C.N. A small-scale solar organic Rankine cycle combined heat and power system with integrated thermal energy storage. Appl. Therm. Eng. 2017, 127, 1543–1554. [Google Scholar] [CrossRef]
- Iasiello, M.; Braimakis, K.; Andreozzi, A.; Karellas, S. Thermal analysis of a Phase Change Material for a Solar Organic Rankine Cycle. J. Phys. Conf. Ser. 2017, 923, 12042. [Google Scholar] [CrossRef] [Green Version]
- Costa, S.C.; Mahkamov, K.; Kenisarin, M.; Lynn, K.; Halimic, E.; Mullen, D. Solar Salt Latent Heat Thermal Storage for a Small Solar Organic Rankine Cycle Plant. In Proceedings of the ASME 2018 12th International Conference on Energy Sustainability Collocated with the ASME 2018 Power Conference and the ASME 2018 Nuclear Forum, Lake Buena Vista, FL, USA, 24–28 June 2018; Volume ES2018-7326, p. V001T08A002. [Google Scholar]
- Costa, S.C.; Mahkamov, K.; Kenisarin, M.; Ismail, M.; Lynn, K.; Halimic, E.; Mullen, D. Solar Salt Latent Heat Thermal Storage for a Small Solar Organic Rankine Cycle Plant. J. Energy Resour. Technol. 2020, 142. [Google Scholar] [CrossRef] [Green Version]
- Alvi, J.Z.; Feng, Y.; Wang, Q.; Imran, M. Modelling, simulation and comparison of phase change material storage. Appl. Therm. Eng. 2019, 170, 114780. [Google Scholar] [CrossRef]
- TVP Solar. Datasheet; HT-Power Product. Available online: https://www.solarthermalworld.org/news/switzerland-flat-plate-solar-thermal-collector-manufacturer-relies-vacuum-technology (accessed on 7 June 2020).
- Voller, V.R.; Cross, M.; Markatos, N.C. An enthalpy method for convection/diffusion phase change. Int. J. Numer. Methods Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Günther, E.; Hiebler, S.; Mehling, H.; Redlich, R. Enthalpy of Phase Change Materials as a Function of Temperature: Required Accuracy and Suitable Measurement Methods. Int. J. Thermophys. 2009, 30, 1257–1269. [Google Scholar] [CrossRef]
- Pereira da Cunha, J.; Eames, P. Thermal energy storage for low and medium temperature applications using phase change materials—A review. Appl. Energy 2016, 177, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Lacroix, M. Numerical simulation of a shell-and-tube latent heat thermal energy storage unit. Sol. Energy 1993, 50, 357–367. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Pei, G.; Alvi, J.Z.; Ji, J. Analysis of a novel solar electricity generation system using cascade Rankine cycle and steam screw expander. Appl. Energy 2016, 165, 627–638. [Google Scholar] [CrossRef] [Green Version]












| Name of the PCM | Mg(NO3)2·6H2O | |
| PCM category | Inorganic | |
| Melting point temperature (°C) | 89 | |
| Latent heat (kJ/kg) | 140 | |
| Density (g/m3) | 1640 | |
| Thermal conductivity (W/m2·°C) | Solid | 0.65 |
| Liquid | 0.50 | |
| Specific heat capacity (kJ/kg·°C) | Solid | 2.50 |
| Liquid | 3.10 | |
| Melting point temperature (°C) | 28.2 | |
| Latent heat (kJ/kg) | 243.5 | |
| Density (kg/m3) | Solid | 861 |
| Liquid | 772 | |
| Thermal conductivity (W/m2·°C) | Solid | 0.358 |
| Liquid | 0.148 | |
| Specific heat capacity (kJ/kg·°C) | Solid | 1.85 |
| Liquid | 2.33 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvi, J.Z.; Feng, Y.; Wang, Q.; Imran, M.; Khan, L.A.; Pei, G. Effect of Phase Change Material Storage on the Dynamic Performance of a Direct Vapor Generation Solar Organic Rankine Cycle System. Energies 2020, 13, 5904. https://doi.org/10.3390/en13225904
Alvi JZ, Feng Y, Wang Q, Imran M, Khan LA, Pei G. Effect of Phase Change Material Storage on the Dynamic Performance of a Direct Vapor Generation Solar Organic Rankine Cycle System. Energies. 2020; 13(22):5904. https://doi.org/10.3390/en13225904
Chicago/Turabian StyleAlvi, Jahan Zeb, Yongqiang Feng, Qian Wang, Muhammad Imran, Lehar Asip Khan, and Gang Pei. 2020. "Effect of Phase Change Material Storage on the Dynamic Performance of a Direct Vapor Generation Solar Organic Rankine Cycle System" Energies 13, no. 22: 5904. https://doi.org/10.3390/en13225904
APA StyleAlvi, J. Z., Feng, Y., Wang, Q., Imran, M., Khan, L. A., & Pei, G. (2020). Effect of Phase Change Material Storage on the Dynamic Performance of a Direct Vapor Generation Solar Organic Rankine Cycle System. Energies, 13(22), 5904. https://doi.org/10.3390/en13225904