A Model of Moist Polymer Foam and a Scheme for the Calculation of Its Thermal Conductivity

Abstract

This paper proposes a method for determining an effective value of the thermal conductivity for moist, highly porous rigid polymer foams. The model of moist foam based on an ordered structure with interpenetrating components was developed in accordance with the moisture distribution in the pore space. With small moisture content, isolated water inclusions are formed, and the pore space is considered as a binary system (vapor-gas mixture and water) with isolated inclusions. With an increase in moisture content, isolated water inclusions merge, forming a continuous layer, and pore space is considered as a binary system of interpenetrating components. The thermal conductivity of the vapor-gas mixture is represented as the sum of the thermal conductivity of the dry gas and the thermal conductivity of the vapor caused by the diffusion transfer of vapor in the pore space, taking into account the coefficient of vapor diffusion resistance. Using the proposed scheme of calculation, a computational experiment was performed to establish the influence of the vapor diffusion, moisture content, and average temperature of the foam on its thermal conductivity.

1. Introduction

Rigid polymer foams are widely used in construction and other industries as an effective thermal insulation. During the operation of building objects, cyclic changes in temperature and humidity of the environment constantly occur, causing hydrothermal degradation of the polymer skeleton in the thermal insulation layer. As a result, the moisture content of the material significantly increases the initial value of its hygroscopic moisture, which leads to a decrease in its heat-insulating properties. The general characteristics of the complicated process of heat transfer in materials are described by the effective thermal conductivity used to determine the thermal properties of building envelopes.

It is obvious that the thermal conductivity of polymer foam depends on the thermal conductivity of the solid polymer skeleton and the substance present in the pores, which in moist materials consists of a vapor-gas mixture and water. While determining the thermal conductivity of such a pore substance, it is necessary to consider the impact of a diffusive moisture flux in the form of water vapor moving in the direction of the heat flow which is accompanied by the phase changes of the moisture (evaporation in the warmer zone and condensation in the colder zone) [1,2,3,4]. At the same time, due to the condensation of the diffusing water vapor, the thermal conductivity of moist materials and, above all, highly porous foams can significantly increase.

There are many formulae for calculating the thermal conductivity of dry heat-insulating materials that have been obtained by various methods over the last one hundred years. Many of them were considered and analyzed in [5,6]. The best formulae were identified, taking into account the highest compliance of calculation results and experimental data. Such consistency of results has not been demonstrated in other papers [3,4,7], in which the Krischer method, or its improvement, is used to calculate the effective thermal conductivity of a moist material. The formulae used in the mentioned works contain empirical coefficients and when using them, significantly different results are obtained. Moreover, when assessing the effect of vapor diffusion on heat transfer the resistance of the porous medium to vapor diffusion is not taken into account or not sufficiently accurately taken into account. The moist foams are considered in only one work [4] and the character of wetting of the polymer skeleton surface with liquid (partial or total) is taken into account only in only one work [3]. It should be noted that in an open cellular structure, the transition from partial to total wetting of the pore surface with liquid is accompanied by a stepwise increase in the effective thermal conductivity of the material.

At present, additive and nonadditive schemes are used to assess the impact of the diffusion of water vapor on heat transport. For example, in [4], the effective thermal conductivity of a moist foam consists of the thermal conductivity caused by condensation of diffusing water vapor determined using the relation analogous to Fourier’s law for the heat flux and of the conductive thermal conductivity of a moist material determined according to Krischer’s equation. Both formulae include empirical coefficients.

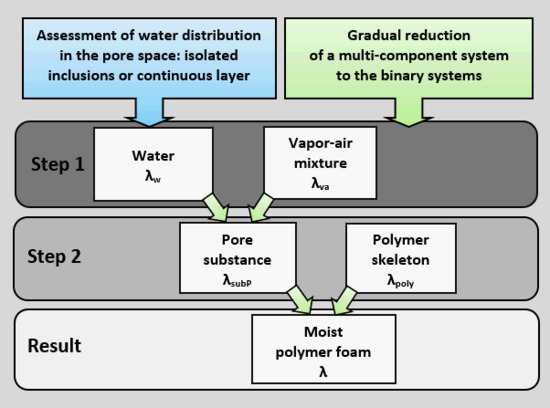
The authors of [3] estimate the impact of the diffusion of water vapor on heat transport using a nonadditive calculation scheme, modeling the moist material as a structure with interpenetrating components. The analysis of a three-component system containing a solid skeleton, water, and a vapor-gas mixture was carried out using the method of gradual reduction of a multicomponent system to the binary one. First, the effective thermal conductivity of a pore substance containing liquid and a vapor-gas mixture (a binary system with interpenetrating components) is determined, and then, the effective thermal conductivity of the moist material consisting of a solid skeleton and pore substance can be calculated. The thermal conductivity of the vapor-gas mixture was represented as the sum of the thermal conductivity of the dry gas and the thermal conductivity of the vapor caused by its diffusion transfer in the pore space.

In highly porous polymer foams, moisture in liquid form wets the pore surface locally (more frequently) or totally (less frequently). In the first case, the pore space can be modelled as a binary system with isolated inclusions, and in the second case as a binary system with mutually interpenetrating components. By changing the material moisture or the contact angle, it is possible to move from one binary system to the other. In order to do this, it is necessary to know the threshold value of moisture or the contact angle. However, in the abovementioned calculation schemes this important feature is not taken into account.

This paper proposes a method for determining an effective value of the thermal conductivity for moist highly porous polymer foams, which uses a nonadditive calculation scheme, including the impact of the vapor diffusion on heat transport, as well as consequent binary systems (a porous substance consisting of a liquid and a vapor-gas mixture, and also a solid polymer skeleton and a porous substance) described with structural models with interpenetrating components and isolated inclusions. Moreover, the conditions for transition from one structural model to the other are determined.

2. Model of the Moist Polymer Foam Structure and Relations for Calculations

Visualization of the structure of various types of polymer foams presented in a series of works [3,4,8,9,10] shows that the rigid polymer skeleton is composed of cells (bars and membranes) with walls mainly in the form of tetrahedrons, pentagons, and hexagons. The main part of the polymer is located inside straight bars with a practically constant cross-section, with a slight increase in thickness in the nodes usually caused by the connection of bars. Therefore, for the determination of the thermal conductivity of rigid polymer and other foams (ceramic, metallic), regular and irregular polyhedrons were used [3,4,10,11]. Particular attention is drawn by the latest approach, in which a special method (Voronoy) was used to model the structure of the cellular material [10]. However, we propose to use the ordered bar structure consisting of identical elementary cells in the shape of a cube. The use of such a simple elementary cell to determine the thermal conductivity of rigid polymer foams is justified in a number of works, for example, [3,4,6]. Additional justification of the dependencies used in this paper is carried out in the following part, comparing the results obtained from the proposed model with the results obtained from the formulae presented in [10], which more accurately reflect the geometric structure of the material.

When assessing the distribution of liquid moisture in the unit cell, it is necessary to take into account the moisture content in the material, ψ, and the contact angle, θ, formed at the interface between solid, liquid, and gas. The analysis of the results of a number of experimental studies carried out in laboratory and field conditions presented among others in [4,12,13] shows that when there is a permanent contact with an environment with variable humidity and temperature, the volumetric content of moisture in polyurethane and phenol foam can reach ψ = 0.06 to 0.07 m³/m³. In order to determine the contact angle θ, the method of a large drop of water (2 to 3 cm³) wetting a flat horizontal polymer surface was used [14]. After five independent measurements of the contact angle, carried out at 20 °C, it turned out that the measured random value is characterized by an arithmetic mean of θ = 56° and a standard deviation of s = 3.2°.

Figure 1a shows the distribution of a very small amount of water in the form of a membrane with a constant cross-section in the corner formed by two perpendicular half-planes at different values of the contact angle. If we adopt the average cell size of polyurethane foam given in [5], it can be assumed that the dimension, x, in Figure 1a does not exceed 200 μm. In this case, in normal conditions, gravity is not able to distort the surface of the liquid shown in Figure 1a because its value does not exceed 0.5% of the surface tension value. Therefore, it is easy to present the distribution of liquid in the unit cell. As an example, Figure 1b shows an eighth part of the unit cell containing insulated inclusion of water at the contact angle of 45°.

As the consequence of the moisture level increases, the dimension, x, rises, shown in Figure 1b. The isolated water inclusions rise until they join in the pore space (at x = L − Δ, where L is the ½ of the unit cell size and Δ is the bar thickness). Then, the pore space should be considered as the binary system with interpenetrating components. Therefore, when calculating the thermal conductivity of a pore space, it is necessary to know the boundary value of moisture content at which transition from the system with isolated inclusions to the system with interpenetrating components takes place.

The volumetric moisture in pores, ψ_P is related to the liquid volume, V_w, and the pore volume, V_p, according to the ratio ψ_p = V_w/V_p and to the volumetric moisture, ψ, and the porosity of material, P, according to the ratio ψ_p = ψ/P. It results from Figure 1b that V_w = (3 x² Δ/2) + (x³/6). The pore volume can be calculated as V_p = (L−Δ)³ + 3Δ (L − Δ)². Assuming that x = L ‒ Δ, after some simple transformations we obtain an equation for calculating the boundary value of the volumetric pore moisture at the contact angle of θ = 45°:

$${\mathsf{\psi }}_{\mathrm{P} }^{\prime }= \frac{1+8·\mathrm{c}}{6·\left(1+2·\mathrm{c}\right)}; \mathrm{c} = \frac{\Delta }{\mathrm{L}}$$

(1)

In a similar way, at the contact angle of ϴ = 90°, we obtain:

$${\mathsf{\psi }}_{\mathrm{P}}^{\prime } = \frac{\mathsf{\pi }·\left(1+3.5·\mathrm{c}\right)}{6·\left(1+2·\mathrm{c}\right)}$$

(2)

At the contact angle of ϴ = 0°, the searched value of boundary moisture content is calculated from the equation:

$${\mathsf{\psi }}_{\mathrm{P}}^{\prime } = \frac{\left(4-\mathsf{\pi }\right)·\left(1+14·\mathrm{c}\right)}{20·\left(1+2·\mathrm{c}\right)}$$

(3)

Equations (1)–(3) determine the dependence between the boundary pore moisture content, ${\mathsf{\psi }}_{\mathrm{P}}^{\prime }$, and the contact angle, ϴ, for different values of the relative size of bars c = Δ/L. Such dependence is shown in Figure 2. The relative size of bars is calculated using the following equation [15]:

$$\mathrm{c} = 0.5+\sin \left[\frac{\arcsin \left(2·{\mathrm{m}}_{\mathrm{i}}-1\right)}{3}\right]$$

(4)

where m_i is the concentration of the i^th component (i = 1, 2), for which the value c is determined.

In order to determine the effective thermal conductivity structure consisting of the two components with concentrations, m₁ and m₂, and thermal conductivity, λ₁ and λ₂, we use the relations determined by means of the justified methods of the generalized theory of conductivity [3]. For the structure with interpenetrating components the relation obtained by G. N. Dul’nev in 1965 was used [3]:

$$\mathsf{\lambda } ={ \mathsf{\lambda }}_1 \left[{\mathrm{c}}^2 + \mathsf{\nu }{\left(1 - \mathrm{c}\right)}^2 + 2\mathsf{\nu }\mathrm{c}\left(1 - \mathrm{c}\right){\left(\mathsf{\nu }\mathrm{c} + 1 - \mathrm{c}\right)}^{-1}\right]$$

(5)

where ν = λ₂/λ₁. The components of this structure are geometrically equivalent, and it does not matter in the calculations which one of them will be adopted first.

The good ability of Equation (5) to predict the thermal conductivity of dry polymer foams has been demonstrated in [6]. Additionally, for four dry samples of polyurethane foam with an open cell structure, the characteristics of which is presented in [10], a comparison was made between the results of calculations obtained based on Equation (5) from this paper and the Formula (16) from work [10], taking into account the variability of the cross-section of bars along their length, t, and the variability of the unit cell diameter in the form of dodecahedrons, CV (12 walls in the form of a pentagon). The following equation was used [10]:

$$\mathsf{\lambda } ={ \mathrm{m}}_2·{\mathsf{\lambda }}_2+\left[1-0.0692·\left(\mathrm{t}-1\right)-0.0347·{\left(\mathrm{t}-1\right)}^2\right] \left[\left(0.9-⅓\mathrm{CV}\right)·{\mathrm{m}}_1{}^2+⅓{\mathrm{m}}_1\right]{ \mathsf{\lambda }}_1$$

(6)

where ${\mathrm{m}}_1 ={ \mathrm{P} \mathrm{and} \mathrm{m}}_2 = 1 -{ \mathrm{m}}_1$.

The thermal conductivity of the hard component λ₁ = 0.25 W/(m·K) (for polyurethane) was assumed in the calculations, and for the gas component λ₂ = 0.026 W/(m·K) (for air). The results of calculations made on the basis of both dependencies, shown in

Table 1. Calculation values of thermal conductivity, λ, of dry foams of open-cell material with porosity, P, determined based on Equation (5) and based on Formula (16) from work [10].

Sample Number	C	m2 = P	λ, W/(m·K) Based on Equation (5)	t	CV	λ, W/(m·K) Based on Formula (16) from [10]
1	0.2240	0.872	0.0395	1.923	0.0346	0.0356
2	0.2032	0.893	0.0371	2.500	0.0246	0.0326
3	0.1542	0.936	0.0324	2.941	0.0339	0.0289
4	0.1157	0.963	0.0296	1.887	0.0434	0.0281

, are similar. The average difference does not exceed the double standard deviation 2σ = 3.08 · 10⁻³ W/(m·K) determined on the basis of experimental data [6,16], which means that with a probability of 95% this difference is statistically insignificant. If we exclude the variability of the cross-section of bars and the variability of the unit cell diameter from Formula (16) from work [10], then the results will be practically the same. Therefore, the use of an ordered bar structure consisting of identical cubic cells is fully justified. The weak influence of the form of elementary cells and cross-sections of bars on thermal conductivity is also indicated in [17].

For the structure with isolated inclusions the following equation should be used [3]:

$$\mathsf{\lambda } ={ \mathsf{\lambda }}_1\frac{\mathsf{\nu }-\left(\mathsf{\nu }-1\right)\left(1-{\mathrm{m}}_2^{2/3}\right){\mathrm{m}}_2^{1/3}}{\mathsf{\nu }-\left(\mathsf{\nu }-1\right){\mathrm{m}}_2^{1/3}},$$

(7)

where m₂ is the volumetric concentration of inclusions, ν = λ₂/λ₁. In this case, the components of the structure are not geometrically equivalent.

For the above case, an analogous comparative calculation was also performed, using data from four, dry closedcell polyurethane foam samples presented also in [10]. Equation (7), proposed in this paper, was used and Formula (11) from work [10] taking into account the variability of membrane thickness, Th_max/Th_min, and the variability unit cell diameter, CV. The following equation was used [10]:

$$\mathsf{\lambda } ={ \mathrm{m}}_2·{\mathsf{\lambda }}_2+\left[⅔·{\mathrm{m}}_1·{\mathsf{\lambda }}_1·\left(1-0.0476·\mathrm{CV}\right)·{\left({\mathrm{Th}}_{\max }/{\mathrm{Th}}_{\min }\right)}^{-0.047}\right].$$

(8)

Table 2. Calculation values of thermal conductivity, λ, of dry closed-cell foams with porosity, P, determined based on Equation (7) and based on Formula (11) from work [10].

Sample Number	m2 = P	λ, W/(m·K) Based on Equation (6)	CV	Thmax/Thmin	λ, W/(m·K) Based on Formula (11) from [10]
1	0.9037	0.0414	0.54	2.67	0.0384
2	0.8519	0.0499	0.67	2.95	0.0448
3	0.9444	0.0348	1.12	2.54	0.0330
4	0.9593	0.0324	1.13	2.14	0.0311

shows a good match between the calculation results of both models.

When calculating the thermal conductivity of moist foam, we consider a mixture of vapor-air as one of the components of the pore substance, because the gas accumulated in the pores of the foam during its production is replaced with air and water vapor by diffusion. According to the papers [1,2,3], the thermal conductivity of the vapor-air mixture, λ_va, is equal to the sum of the thermal conductivity of air, λ_a, and water vapor, λ_v. The thermal conductivity of water vapor, λ_v, due to its diffusion in the pore space is determined on the basis of Equation [3]:

$${\mathsf{\lambda }}_{\mathrm{v}} = \frac{\mathrm{D}}{\mathsf{\mu }}·\frac{\mathrm{M}}{\mathrm{R}·\mathrm{T}}·\frac{{\mathrm{p}}_{\mathrm{va}}}{{\mathrm{p}}_{\mathrm{va}}-{\mathrm{p}}_{\mathrm{v}}}·\frac{{\mathrm{dp}}_{\mathrm{v}}}{\mathrm{dt}}·{\mathrm{q}}_{\mathrm{t}}$$

(9)

where:

• D is the coefficient of water vapor diffusion in stationary air, m²/s;
• μ is the coefficient of resistance to vapor diffusion in the pore space;
• M is the molecular weight of water vapor, kg/mol;
• R is the universal gas constant, J/(mol K);
• T is the temperature of water vapor, K;
• p_va is the total vapor and air pressure, Pa;
• p_v is the partial vapor pressure, Pa;
• q_t is the specific heat of evaporation at the temperature T, J/kg.

When determining the coefficient D, the relation formulated by Schirmer, in 1938, is widely used [17,18]:

$$\mathrm{D} = \frac{2.305·{10}^{-5}{\mathrm{p}}_{\mathrm{o}}}{{\mathrm{p}}_{\mathrm{va}}}·{\left(\frac{\mathrm{T}}{273}\right)}^{1,81},{\hspace{1em}\hspace{1em}\mathrm{p}}_{\mathrm{o}}=101323\mathrm{Pa}.$$

(10)

The experimental value of the coefficient μ is determined from the relation:

$$\mathsf{\mu } = \frac{\mathrm{D}}{{\mathsf{\delta }}_{\mathrm{v}}},$$

(11)

where δ_v is the vapor permeability coefficient of the porous material, m²/s. Experimentation can be avoided by choosing from the large number of proposed formulae the most suitable one for the considered material. Preliminary analysis shows that for moist polymer open-cell foam with the concentration of a vapor-air mixture m − ψ ≥ 0.93, the simple equation can be proposed [4]:

$$\mathsf{\mu } = \frac{1}{0.57·\left(\mathrm{m}-\mathsf{\psi }\right)}.$$

(12)

When m − ψ < 0.93 it is possible to use the relation [18]:

$$\mathsf{\mu } = \frac{{\mathsf{\tau }}^2}{\mathrm{m}-\mathsf{\psi }},$$

(13)

where τ is the tortuosity coefficient, which according to [19] can be determined from the relation:

$$\mathsf{\tau } = \frac{\left(\mathrm{m}-\mathsf{\psi }\right)}{{\mathrm{c}}^2}.$$

(14)

In the above formula the parameter $\mathrm{c}$ is calculated from Equation (4) for m₁ = m − ψ. After substituting the relation Equation (14) into the Equation (13) we will eventually obtain:

$$\mathsf{\mu } = \frac{\left(\mathrm{m}-\mathsf{\psi }\right)}{{\mathrm{c}}^4}.$$

(15)

It seems useful to calculate the diffusion component of thermal conductivity, λ_v, for foams with moisture reaching the maximum hygroscopic value, ψ_h, with a constant pressure of saturated vapor, p_vh, at a given temperature.

3. Calculation Scheme

The effective thermal conductivity of the three-component system was determined by the method of gradual reduction of a multicomponent system to the binary one [3]. We will illustrate the recommended calculation scheme by calculating the effective thermal conductivity of a foam sample having porosity of P = 0.93, density ρ = 80 kg/m³, moisture content ψ = 0.06 m³/m³ close to the highest operational value, average temperature t = 20 °C, and contact angle ϴ = 60°.

First, using Equation (9), we calculate the diffusion component of thermal conductivity, λ_v, with T = 293 K, p_va = 10⁵ Pa. According to data found in literature and the equations presented in [17] it is assumed that M = 0.018 kg/mol, R = 8.3144 J/(mol·K), p_v = p_vh = 0.02338·10⁵ Pa,

dp_v/dt = 148 Pa/K (with dT = 1K), and q_t = 2.38·10⁶ J/kg. Using Equation (10), we determine the diffusion coefficient of vapor in air, D = 2.65·10⁻⁵ m²/s. Equation (15) is used to calculate the coefficient, μ, with the volumetric concentration of the vapor-gas mixture m = 0.93 − 0.06 = 0.87 and the parameter c = 0.7743 calculated from Equation (4) with m₁ = m = 0.87. Then, we have μ = 2.42. As a result, we obtain λ_v = 0.03 W/(m·K). Assuming thermal conductivity of dry air λ_a = 0.0257 W/(m·K), the thermal conductivity of the water vapor and air mixture is λ_va = λ_v + λ_a = 0.0557 W/(m·K).

The volumetric content of water in the pore space (pore moisture) is ψ_p = ψ/m = 0.06/0.93 = 0.0645 m³/m³. With the contact angle ϴ = 60° and the parameter c = 0.1614 calculated from Equation (4), the volumetric concentration of solid polymer m₁ = 1 − P = 1 − 0.93 = 0.07, the threshold value pore moisture content read from Figure 3 is ψ_p’ = 0.38 m³/m³. It exceeds the actual ψ_p = 0.0645 m³/m³ nearly six times. In a case like this, the pore space containing the vapor-gas mixture and water is considered as a binary structure with isolated inclusions. One component of this system is the vapor-gas mixture with the volumetric concentration m₁ = 0.9355 and thermal conductivity λ₁ = λ_va = 0.0557 W/(m·K), and the other component is water with the volumetric concentration m₂ = 0.0645 (m₁ + m₂ = 1) and thermal conductivity λ₂ = λ_w = 0.596 W/(m·K). At this point Equation (7) is used to calculate the effective thermal conductivity of the pore substance λ₁₂ = 0.0608 W/(m·K) with the relation ν = λ₂/λ₁ = 0.596/0.0557 = 10.7. Now, using Equation (7) with the ratio ν = λ₂/λ₁ = 0.596/0.0557 = 10.7, we calculate the effective thermal conductivity of the interpore substance λ₁₂ = 0.0608 W/(m·K).

Finally, using Equation (5) for the structure with equivalent, interpenetrating components, we determine the effective thermal conductivity, λ, of moist polymer foam. The first component to be considered is the pore substance, for which we have m₁ = m = 0.93, λ₁ = λ₁₂ = 0.0608 W/(m·K) and the parameter c = 0.8386, determined from Equation (4). The second component, the polymer skeleton, is characterized by the values m₂ = 0.07 and λ₂ = 0.25 W/(m·K). Then, we have the ratio ν = λ₂/λ₁ = 0.25/0.0608 = 4.1118. After we obtain the values of the parameters, c and ν, from Equation (5), we determine the effective thermal conductivity of polymer foam λ = 0.068 W/(m·K).

For comparison, the abovementioned scheme was used to calculate the thermal conductivity of a porous substance, λ₁₂, without including the heat transport result of the diffusive condensation of water vapor, λ_v. In this case, the value of the effective thermal conductivity of moist polymer foam was λ’ = 0.0354 W/(m·K), which is nearly half of the result of the previous calculations. If we use the additive calculation scheme and consider the effective thermal conductivity of moist foam as the sum λ = λ’ + λ_v, then we will obtain the result λ = 0.0354 + 0.03 = 0.0654 W/(m·K), which is less than the value determined with the nonadditive scheme by only 3.8%. It is also noteworthy that during the application of another additive scheme with the formulae suggested in [4], including empirical coefficients, the effective thermal conductivity value is λ = 0.0745 W/(m·K), and it is greater by 9.6% than the value determined with the nonadditive calculation scheme suggested in this paper. We obtain the identical result if we use in the suggested scheme the value of the water vapor diffusion resistance coefficient μ = 2.016 calculated from Equation (12).

4. Calculation Experiment and Its Results

The calculation experiment was carried out to assess the effect of moist content, ψ, at the average temperature, t, of the considered polymer foam on its thermal conductivity, λ. The proposed example of calculating, λ, which takes into account different approaches for estimating its value, was repeated for different levels of moisture content in the range 0.01–0.3. According to the results of the repeated calculations, the graph was constructed reflecting various dependencies of λ on ψ, as shown in Figure 3, together with experimental data taken from [4].

From the comparison of the Dependence 1 in Figure 3 with the other dependencies it follows that the diffusion component of the thermal conductivity, λ_v, is different for various ways of taking into account thermal conductivity, λ, of moist polymer. Using Equation (12) to determine the vapor diffusion resistance coefficient, µ, instead of Equation (15) resulted in significant differences (qualitative and quantitative) while determining the effective thermal conductivity, λ (Curves 3 and 4).

A comparison between Dependencies 2 and 3 shows that the additive and nonadditive schemes for calculating the diffusion component, λ_v, bring similar results within the maximum operating moisture content ψ ≤ 0.07. In this case, the results of the nonadditive calculation scheme exceed the results of the additive scheme by not more than 4%. As the moisture level in the material increases up to ψ = 0.3, this difference increases to 15%.

Figure 3 shows that with the moisture content, ψ > 0.2, the experimental data for the same material by some authors (triangles) exceed nearly two fold the experimental data by other authors (circles), and the estimated Curve 3, obtained from the calculation scheme suggested in this paper, adequately predicts the experimental data marked with circles. Moreover, the experiments show [3] that the thermal conductivity of the same material with the same moisture can vary considerably. This can be primarily explained by the character of the wetting of the polymer skeleton with liquid (partial or total), the character of the distribution of moisture in the volume of the test sample (even or uneven), the measurement method (stationary or nonstationary), etc. On the basis of the results of experimental and theoretical studies, the conclusion was made in [4] that all attempts of taking into account the impact of moisture exchange processes in protective layers on their thermal insulation properties by using, in the calculations, the effective thermal conductivity measured for moist materials by stationary and nonstationary methods give unsatisfactory results. For the polymer foam discussed in this paper (m = 0.93 and ψ = 0.3) the pore moisture content is ψ_p = ψ/m = 0.323, for which the threshold value the contact angle is θ’ = 52° (Figure 2). The pore surface is completely wetted with water, and the pore space can be represented as a binary system with interpenetrating components, for which Equation (5) is used to calculate thermal conductivity. In this case, the value of the effective thermal conductivity of moist polymer foam is λ = 0.136 W/(m·K) and it is 1.71 times higher than the value of thermal conductivity calculated for the same material when the pore surface is partially wetted (ϴ > 52°), and it predicts accurately enough the experimental value λ = 0.15 W/(m·K), as shown in Figure 3. For a different moisture content of ψ = 0.25 (ψ_p = 0.269) and the contact angle ϴ < 45° the calculated value is λ = 0.121 W/(m·K) and it is close to another experimental result, λ = 0.13 W/(m·K) (Figure 3). Thus, with the correct quantitative assessment of the character of the wetting of the pore surface with liquid (partial or full), determined using the parameters ψ_p (ψ) and ϴ, the proposed method for calculating the thermal conductivity of foams λ can satisfactorily predict the experimental data.

The calculations confirmed the well-known effect of increasing the thermal conductivity of moist polymer foams with an increase in its temperature. Moreover, within the operational moisture content of the material, ψ ≤ 0.07, the difference between the thermal conductivity values calculated by the additive and nonadditive calculation schemes did not exceed 4%. With increasing moisture content of the material to ψ = 0.3, this difference increases, which is shown by Curves 2 and 3 in Figure 4.

5. Conclusions

The geometric model of moist foam has been developed, which makes it possible to find a method for determining the boundary moisture content of pores or the contact angle at which the transition from partial wetting of the pore surface with liquid to full wetting occurs and vice versa. Calculations show that such a transition is accompanied by a step change in the thermal conductivity of foams. The mathematical description of the heat transfer process in the model structure of moist foam was performed taking into account the diffusion of water vapor in the pore space. Moreover, using the additive and the nonadditive scheme for including the diffusion component of thermal conductivity it was shown with calculations that there was a significant impact of moisture content and the average temperature of polymer foam on the effective thermal conductivity. The comparison between the results of the calculations and the experimental data showed that they were sufficiently consistent.