Coordinated Control of Aichi Microgrid for Efficient Power Management Using Novel Set Point Weighting Iterative Learning Controller

Abstract

A novel Set Point Weighting Iterative Learning Controller (SPW-ILC) has been proposed for voltage stabilization at AC/DC bus, coordinated control among the distributed sources in the modeled hybrid microgrid (HMG) and synchronization of HMG with utility grid. The Aichi Micro grid test system located at Aichi Institute of Technology, Japan has been considered for the simulation studies and modeled in MATLAB/Simulink environment. The Aichi microgrid can be operated in autonomous mode as AC system and DC system. When it is working as DC system, the dc bus voltage is maintained stable by incorporating dedicated fuzzy logic controllers (FLC) for DC-DC converters due to the variable distributed sources. Meanwhile, the bidirectional converter also called as Interlinking Converter (IC) located between ac bus and dc bus controlled by proposed SPW-ILC converts the DC voltage into AC voltage and meets AC loads. In AC system of autonomous mode, the inverters are controlled by proposed controller to meet the ac demands. The grid connected mode of Aichi microgrid system is performed by properly controlling the IC to meet ac and dc loads. The proposed SPW-ILC reduces the voltage deviation and maintains the power balance under variable source and load conditions. The results have been compared with the conventional proportional integral (PI) controller and FLC to validate the performance of the controller. The results show that the proposed SPW-ILC has efficiently control the voltage and maintain the power balance.

1. Introduction

Micro grids are defined as the low voltage distribution network modeled with distributed energy sources such as solar system, wind turbine, fuel cell, diesel generator, micro turbine; energy storage devices and loads. Micro grids find pervasive applications in the power sector in many forms; AC microgrid, DC microgrid and Hybrid microgrid. Both AC and DC power sources enhance the micro grid to provide reliable supply. Due to the intermittent nature of the renewable energy sources, microgrid need to be connected with the utility grid for uninterrupted power supply. A microgrid could be operated in autonomous mode or grid connected mode to improve the reliable power distribution. Coordinated control of the distributed sources, battery and the loads in the microgrid is necessary to satisfy the power balancing constraint which could be achieved by two level of controls namely primary/source level /local control and the secondary/system level /master control. In source level control, the control of the power electronic converters between the sources and the bus voltages is being done. This control is needed to maintain the common bus voltages at constant and will be accomplished basically by controlling their dedicated converters. In master level control, the power flow in the microgrid from various sources, battery and loads has to be balanced for the system stability point of view. This will be achieved by the coordinated control of the sources and loads in different mode of operation.

The major technical challenges in the microgrid include voltage and power stabilization in island/grid connected mode, economic and effective integration of multiple power sources with storage devices. Among the major issues, power and voltage control plays a significant role in the microgrids since frequency is related to real power control (P-f) and voltage is related to reactive power (Q-V) control. The power management has been done by the active power control [1,2], reactive power control [3,4], AC/DC bus voltage control [5,6,7], storage control [8,9,10] and control of interlinking converters [11,12]. AC microgrids are employing real power and reactive power droop control, whereas DC microgrids are adopting voltage and current droop control methods [13]. In autonomous mode, DC bus voltage control has been performed with the energy storage devices and its boost converter. AC bus voltage can be controlled by the droop based inverter. In grid connected mode, Interlinking Converters (ICs) are responsible for controlling DC bus voltage. With the ratio of power to dc voltage droop control, the dc storage control for maintaining the dc bus voltage along with stability has been proposed in [8]. Control of power flow through droop control method has significant variation in frequency, low voltage quality and low stability [14]. Simultaneous control of bus voltages and the power could not be achieved by droop control method alone [15].

The suitable method to overcome the drawbacks of the droop control method is to design a centralized or hierarchical controller that has the ability to maintain the voltage constant and also efficient power sharing among the Distributed Generators (DG’s). Hierarchical control can be divided into voltage control, primary control and tertiary or secondary control [16]. Voltage control is mainly responsible for tracking the reference grid voltage which includes voltage and current control loops. Primary control enhances the performance and stability of the microgrid, sustains the voltage and frequency, offers plug in features for DG’s, ensures efficient power sharing with different loads, removes the circulating current. Secondary control finds the voltage and frequency at point of common coupling (PCC) and changes the reference values for the primary control. This control determines power generation and demand in the microgrid to obtain optimum operating points for the DGs. Secondary control is referred as central control or supervisory control.To achieve the bus voltage control and power flow control, suitable controllers has to be designed and implemented in the microgrid.

Controllers can be of repetitive and non-repetitive in nature. Controller based on disturbance observer for bus voltage control [17] and controller with data driven model free voltage for the IC’s control of AC and DC bus voltages have been proposed [15]. Fuzzy logic based energy management system has been proposed for microgrid operation in [18]. An optimized Fuzzy- PID (Proportional Integral and Derivative) based controller has been presented in [19] for frequency stabilization of two area system. Fractional order (FO) PID controller has been proposed for the inverter operation in [20] to remove the amplitude and phase shift error and to reduce the total harmonic distortion (THD) of the current and in [21] for boost converter operation with multi objective optimization. A repetitive controller takes the reference signal and the disturbance parameters repetitively either explicitly or implicitly to reduce the control errors [22]. Repetitive controllers are classified as multi resonant control which can be applied only to continuous repetitive process and Iterative Learning Control that can be used for both continuous and batch type of control action. Since iterative learning control is more versatile and used for continuous and batch type, it has been adopted widely in many applications. Using internal model principle (IMP), the iterative learning controller (ILC) which is a type of repetitive control has been utilized as mentioned in [23] to eliminate the periodic errors. ILC is being considered as the practical control method for improving the transient response of any system having repetitive action by incorporating the information about the error obtained from the previous iteration for controlling the next iterations. Hence, high performance could be achieved with low tracking error for the system operating under uncertain and disturbing conditions.

ILC has been patented for actuator’s control in US by Garden in 1971 and it has applied to the academic field in 1978 by Uchiyama [24]. Arimoto [25] named the ILC in 1984 which had been applied for industrial driving applications especially for voltage control of the DC servo motor. The utilization of ILC twigs from robotics industry for repetitive actions. ILC has been considered as an intelligent control method to overcome the drawbacks of the conventional controller for obtaining the desired transient response.

A nonlinear ILC (NILC) [26] has been used for nonlinear multi input/ output mechanical systems with robotic manipulators. An ILC based on error tracking scheme [27] has been proposed for non-linear time delay systems under non-identical initial condition to attain desired error trajectory. A novel ILC [28] have been proposed for updating the control input based on both past trails and predicted future trails from the details of the plant model. The trajectory tracking [29] has been proposed for non-linear systems by considering state dependent uncertainties using both feedback ILC and Repetitive Learning Control (RLC).

Iterative Learning Control algorithm has been found in many applications such as robotics industries, bioengineering, micro propulsion, wafer stage motion systems, high resolution electrodynamic jet printing and the power systems also. As the renewable energy sources have variable input, the role of controllers is inevitable in the microgrid system. The feedback controllers measure the output of the system or plant;then influence the input towards the desired set point. Conventional Proportional Integral(PI) controllers have been used in the microgrid applications for many years and are mainly used to eradicate the steady state error. Nevertheless, the speed of the response and the stability is concerned, PI has negative impact which makes PI controller less suitable for microgrid applications. Now a days, the concept of fuzzy logic has been implemented in various control applications in successful manner. Unlike the traditional control methods, fuzzy control doesn’t need the model of the system and the objective functions in very precise manner. On the other hand, many assumptions have been taken with the fuzzy control such as: the plant is observable and controllable; there is a solution for the system. The main drawback of fuzzy control is that it doesn’t consider the stability and may end up at local optimum which is the major concern in microgrid applications.

The appropriate solution for the above issues in the controllers could be the ILC. The main idea behind the selection of ILC for microgrid applications is to exploit the system repetitions to enhance the performance of the system. The major advantage of ILC is that the transient behavior and tracking output of the system could be improved for uncertain dynamic systems which drive repetitively. Thus the ILC could be termed as a repeated control method that trusts on less calculation and needs less prior information about the system. It has the advantages of good tracking performance with less error; no separate algorithm is needed to connect ILC with other controllers. When ILC is implemented in the microgrid, the deviation in the voltage and frequency is considerably reduced which will make the system more stable and reliable.ILC has been developed and utilized for many industrial applications as mentioned in the literature. Few researchers have implemented ILC for microgrid applications [22,30]. Due to its repetitive nature, ILC has been considered as the most suitable controller for the voltage control and power management. Hence in this paper, ILC has been implemented in the practical test system of Aichi microgrid and simulation studies has been carried out in MATLAB/SIMULINK.

Aichi microgrid system is located in Aichi Institute of Technology (AIT), Japan [31]. Building 12 and Library are interconnected to exchange the power between the areas depending on the power availability and the load demand. Among this, Building 12 of Aichi microgrid is considered as test system for simulation studies of the proposed work and it has both ac and dc bus systems to meet the customer demands. The power from DGs is supplied to the DC loads and battery via DC-DC converters and AC loads obtain power through the inverters. A bidirectional converter is used between ac/dc bus for controlling the power flow among the sources and load. The uniqueness of this test system is that no outage can be incurred in the system even in the case of utility grid failure [31]. The system consists of a solar system, two wind turbines and battery that have dedicated DC-DC converters with controllers to maintain output voltage constant under variable input conditions. The ILC has been proposed for the inverters of the DG’s and for the IC connected between ac and dc bus in the microgrid. The role of ILC in this proposed work is to maintain the bus voltages within the limits under load variations.

Due to the improved voltage profile, the power loss in the system is reduced which will be an important factor in economical point of view. The power management in the hybrid microgrid has been realized effectively with the proposed ILC. The main contribution of the paper is to design and development of ILC for the hybrid microgrid applications by introducing a novel set point weighting factor in the ILC to enhance its performance; stability analysis of ILC with various configurations; implementation of proposed ILC in the practical test of aichi microgrid to maintain the stable voltage and frequency along with the power management under various modes of operations such as source and load variations.

The paper is organized in the following manner: The introduction of hybrid microgrid, challenges in the microgrid, need for controllers, types of controller and role of ILC in various applications is discussed in Section 1. The microgrid system description and modeling of various components in the micro grid have been elaborated in Section 2. The basics of iterative learning controller, the types of ILC and selection of ILC for this application depending upon the stability studies have been discussed in Section 3. The implementation of ILC in Aichi microgrid with the inner and outer control loops has explained in Section 4. The case studies in different modes of simulation studies, the results and inferences for the case studies have been discussed in Section 5. The conclusion and the future scope of the paper is presented in Section 6.

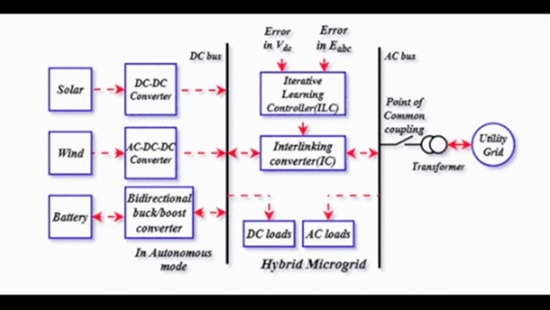
2. Formation of Micro Grid

2.1. System Description

Building 12 of AIT microgrid as shown in Figure 1 has a single PV system of 10 kW; two wind generators rated 10 kW and 2 kW as distributed generators. Since, the output voltage from these DG ’s are very low, each DG has been connected to DC-DC converter to boost its voltage into 220 V. The DC bus is connected to the battery which is of VRLA (Valve Regulated Lead Acid) type.The DG’s have separate inverters to convert into AC which is connected to AC bus maintaining at 415 V. There is a bi-directional or interlinking converter located between AC bus and DC bus to facilitate the battery charging and discharging operation and also for bi-directional power flow. The AC bus is connected into the Utility grid and also to Diesel generator through an ACSW (AC Switch). Both AC and DC loads have been connected to its respective buses. For the simulation analysis, it is most important to model the major components in the microgrid for delivering the desired output.The modeling of the solar, wind turbine and the battery has been discussed in the following section.

2.2. System Development

2.2.1. Solar Cell

The solar cell model is being considered with current source, a diode, combination of series and parallel resistances and its equivalent circuit is shown in Figure 2.

The current is determined by the following Equations (1)–(4):

$$I_{pv}=N_p{I}_{ph}-N_p{I}_d$$

(1)

$$I_{ph}=\{I_{sc}+K_1(T_c-T_{ref})\}\frac{\lambda }{1000}$$

(2)

$$I_d=I_s\left[e^{\frac{qU}{N_{s}k{T}_{c}A}}-1\right]$$

(3)

$$I_s=I_{rs}{\left[\frac{T_c}{T_{ref}}\right]}^3{e}^{(\frac{q{E}_g\left[\frac{1}{T_{ref}}-\frac{1}{T_c}\right]}{kA})}$$

(4)

where $I_{pv}$, $V_{PV}$ are the solar output current (A) and voltage (V) respectively; $I_d$, $I_{ph}$, $I_{sc}$ are current (A) from the diode, current (A) generated and short circuit current (A) respectively. $\lambda$ is the radiation (W/m²); $I_s$, $I_{rs}$ are saturation and reverse saturation currents (A) respectively. A is the ideality factor, $E_g$ is the energy in band gap (1.1 eV); $N_s$, $N_p$ are the number of solar cells connected in series and parallel respectively; $K_1$, k are temperature coefficient (A/°C), Boltzmann constant (J/K) respectively; q is the electron charge (C). $T_{ref}$, $T_c$ are the reference, solar cell temperature (K) respectively.

Due to the intermittent nature of the solar irradiation, a DC-DC boost converter has been implemented to regulate the solar output voltage with fuzzy based Maximum Power Point Tracking (MPPT) controller. The inputs to the fuzzy controller are the error and change in error. Error is the rate of change of power with respect to voltage.

The Equations (5) and (6) gives the basic form of inputs to the fuzzy logic controller

Error

$$E(\kappa )=\frac{dp}{dv}=\frac{P_{ph}(\kappa )-P_{ph}(\kappa -1)}{V_{ph}(\kappa )-V_{ph}(\kappa -1)}$$

(5)

Change in Error

$$CE(\kappa )=E(\kappa )-E(\kappa -1)$$

(6)

where $P_{ph}$ ($\kappa$) is the solar power, $V_{ph}$($\kappa$) is the solar voltage, E($\kappa$) is the error calculated by change in solar power with respect to change in solar voltage, CE($\kappa$) is the change in error E($\kappa$), $\kappa$ represents the sample time. The equivalent circuit of the solar cell and its current, power derivation has been referred from [32]. The power from solar has been extracted maximum with the fuzzy based MPPT controller to obtain pulses for the DC-DC converter and the control circuit is shown in Figure 3. The gate pulse from the Fuzzy MPPT controller controls the output voltage of the solar converter. Thus, by altering the ON time of the switch, the output voltage can be altered. Thus, for the given duty cycle “D” the average output voltage $V_{dc}$ (micro grid DC link voltage) of the converter can be computed from the cell output voltage ($V_{PV}$) as follows:

$$V_{dc}=\frac{V_{PV}}{1-D}$$

(7)

2.2.2. Wind System

The wind system is modeled with a DFIG (Doubly Fed Induction Generator), a rectifier, a DC-DC converter with Fuzzy controller. The fixed pitch angle turbine has to be stopped during high wind speed to avoid damage to the wind turbines. To extract power from high wind speed, the generator has to be operated at its maximum speed [33]. Fuzzy Logic Controller (FLC) is used for maintaining the output voltage of DC-DC converter in constant level. Error in induction generator speed and change in error are the inputs for the FLC of wind systems. The actual mechanical power from the rotor is calculated as in Equation (8):

$$P_{\omega }=\frac{1}{2}\rho A{V}^3{C}_p$$

(8)

where $\rho$ is air density, A is the area through which wind is flowing, V is the wind speed, $C_P$ is power coefficient and the maximum value is called as Betz limit or rotor efficiency. The value of $C_P$ depends on tip speed ratio $\lambda$ which is defined as the ratio of wind speed to the turbine angular speed [34] and the maximum value of $C_P$ is 0.59. The wind turbine control circuit is shown in Figure 4.

2.2.3. Battery

Modeling of battery has been considered as in [32] as shown in Figure 5. The voltage output of the battery is formed as in Equation (9):

$$U_{batt}=E_o-K\frac{\int I_{b}dt}{Q_o}-R_b{I}_b$$

(9)

where $E_o$ is the ideal voltage of the charged battery (V), K is the constant that depends on the battery. $R_b$ is internal resistance ($\Omega$) of battery. $I_b$ is battery discharge current (A). $Q_o$ is the capacity of battery (Ah). $\frac{\int I_{b}dt}{Q_o}$ is the discharge status of the battery and ${\eta }_c(t)$ is the coulombic efficiency. The control circuit of the battery is shown in Figure 6. FLC has been used to obtain stable output voltage at DC bus. The difference in actual dc bus voltage and the reference voltage is given to the FLC along with change in error. This FLC generates pulse for the DC-DC converter to regulate voltage at the Battery output.

The equivalent circuit for battery control is shown in Figure 6.

The basics of the proposed controller and the selection process based on its stability has been discussed in the next section.

3. Iterative Learning Controller

ILC has been majorly utilized in robotics applications due to its inherent property of repetitive actions. The general ILC learning rule is in the form of Equation (10) [30] and its structure is shown in Figure 7.

$$u_{i+1}(z)=u_i(z)+k\varphi (z)e_i(z)$$

(10)

where $u_i$ & $u_{i+1}$ is the z transform of the command signal at iteration i & (i + 1) respectively, k is the learning gain, $\varphi (z)$ is the Proportional controller transfer function, $e_i$ is the z transform of the error signal at iteration i, $y_d$ is the desired output and $y_i$ is the actual output.

The Equation (10) is employed in direct Proportional ILC (P-ILC) when the present error and past command signal is known. The inclusion of forgetting factor as shown in Figure 8 in the ILC, increases the controller robustness under the noise, initialization error and system dynamics [30] and it is expressed in Equation (11):

$$u_{i+1}(z)=(1-\alpha )u_i(z)+k\varphi (z)e_i(z)$$

(11)

where $\alpha$ is the forgetting factor in ILC loop.

To prevent the over learning of the controller, the Equation (11) can also be realized with a low pass filter Q(z) [35] as represented in Equation (12) and it is shown in Figure 9.

$$u_{i+1}(z)=Q_{LPF}{u}_i(z)+k_{RC}{e}_i(z)$$

(12)

where $Q_{LPF}$ is the transfer function of the low pass filter in the ILC loop and $k_{RC}$ is the controller gain.

The above process is an integrative action performed from one iteration to next. Generally, this ILC has been designed as plug in controllers. They can be plugged in to the existing non repetitive control system. The main advantage of having ILC as plug in device is that; there is no additional separate algorithm needed for making interaction between ILC & other controllers.

3.1. Selection of ILC Type

As mentioned in the previous section, ILC could be implemented with the forgetting factor $\alpha$ in the feedback loop as in Figure 8 or using a low pass filter with the transfer function of Q(Z) as in Figure 9. In this paper, Iterative learning controller has been implemented with various values of $\alpha$ & with different transfer function low pass filter values and further the stability of the system with the above two cases have been analyzed. From the theory of internal model principle, the periodic signals could be modeled as a memory loop that produces the output at multiple of frequencies n $\omega$, where n = 0, 1, 2, 3 etc. and $\omega$ is the angular frequency. The total number of memory places required to store the previous iteration data could be defined as the ratio of the signal period with the fundamental frequency T = (1/f) and the sample period with sampling frequency $T_s$ = (1/$f_s)$. The transfer function of the memory loop for the circuit shown in Figure 10 has been evaluated as in Equation (13).

$$\frac{u(z)}{e(z)}=\frac{z^{-N_o}}{1-z^{-N_o}}$$

(13)

where

$$N_o=\frac{T}{T_s}$$

(14)

In this simulation, the sampling period is

$$T_s=50\mathsf{\mu }\mathrm{s}\&T=\frac{1}{f};$$

(15)

‘f’ is the fundamental frequency of 50 Hz. Hence

$$N_o=\frac{20(\mathrm{ms})}{50\mathsf{\mu }\mathrm{s}}=400$$

(16)

In Figure 10, the transfer function of ILC with the inclusion of forgetting factor and low pass filter in the feedback path is formulated as Equations (17) and (18) respectively:

$$\frac{u(z)}{e(z)}=\frac{z^{-400}}{1-z^{-400}(1-\alpha )z^{-2}}$$

(17)

and the transfer function with low pass filter is

$$\frac{u(z)}{e(z)}=\frac{z^{-400}}{1-z^{-400}Q(z)z^{-1}}$$

(18)

Based on the frequency characteristics of ILC with forgetting factor shown in Figure 11 and low pass filter shown in Figure 12, it is inferred that the gain margin of the system with forgetting factor ILC is having consistency compared to the filter ILC system. The stability of the system with this forgetting factor is also improved. Hence, the authors have chosen the forgetting factor ILC for the grid tied microgrid controller applications and implemented in the AMG system.

3.2. Selection of Forgetting Factor Value

The authors have introduced novel set point weighting factor $\beta$ with the range of (0–1) in the ILC to reduce the deviation in the dc bus voltage as in Equation (19).

$$u_{i+1}(z)=\beta (1-\sqrt{\alpha })u_i(z)+k_{RC}{e}_i(z)$$

(19)

The proposed HMG has been tested with various $\alpha$ values in the range of (0.005–0.05) [30] and with set point weighting factor ILC. From Figure 13, it has been shown that the overshoot has been reduced with SPW-ILC, though the Integral Absolute Error (IAE) & Integral Time Absolute Error (ITAE) have been slightly increased. In addition to that, the objective of providing stable frequency and voltage is also achieved with the proposed SPW-ILC. And, the smooth transition between the grid connected and autonomous mode of operation with the coordinated control of the sources, storage devices and loads could be achieved.

From the simulation studies, it is proved that the set point weighting factor ILC has better control over the voltage and frequency in all the modes of operation and have efficient power sharing compared to other controllers. Hence, SPW-ILC has been chosen for the simulation studies. Based on the features of ILC especially robust under parameter uncertainty, improved transient response, enhanced convergence characteristic, fast error tracking and minimized error, it has been preferred to control the Grid Side Converter (GSC) and the inverters in the microgird. The main task of GSC with ILC controller in this work is as follows:

• To effectively synchronize the microgrid AC power with the main grid by ensuring the high quality and efficient power exchange between the microgrid and the utility grid.
• To maintain the constant DC-link voltage by minimizing the error between the measured voltage and the reference voltage under wind dynamics, solar insolation.
• To maintain the system stability during mode transition between grid connected and autonomous mode or vice versa. Due to the above highlighted advantages of ILC, it has been implemented in the system as discussed in the next section.

4. Implementation of SPW-ILC in Micro Grid

In grid connected microgrid systems, there are two control objectives.

(1)

Control of source or machine side converter (MSC)

(2)

Control of Grid side converter (GSC).

For MSC, active power control and tracking of maximum power from the renewable sources are the main control objectives. In this work, dedicated fuzzy controllers have been implemented to run the distributed sources in MPPT mode when excess power generation is available or to run in constant power mode when the system is lightly loaded.The control objectives for the GSC are to control & regulate the DC link voltage and to control the reactive power injection to the utility grid. The voltage control of GSC consists of two control loops working in cascaded mode. (1) Inner control loop for current regulation (2) Outer control loop for DC voltage regulation.

The controller implementation for the power conversion of HMG is displayed in Figure 14 and Figure 15. The output current at inverter is converted into dq axes currents using Park’s transformation. The angle for this transformation has been obtained from the Phase Locked Loop (PLL) which has utilized the grid voltages. The d axis reference current for the inner control loop has been acquired from the voltage control loop. ILC has been implemented in this work for the voltage control in the outer loop. Since voltage control is selected, the reactive power control is inherent here, hence the reference current of q axis is considered as zero. The dq axes voltages have been developed from the current control loop, which in turn transformed into abc voltages using inverse Park transformation. Pulse Width Modulation (PWM) technique has been implemented for obtaining the pulses to the IC. The ILC has been implemented for inverter, inverter and inverter control as shown in Figure 14. It has been implemented for IC control as shown in Figure 15.

4.1. Inner Control Loop for Current Regulation

The objective of the current controller is to control the output current of the converter by developing output reference voltage. For the developed HMG, the voltage equations can be written in d-q axis frame by applying KVL from Equations (20)–(23) [36].

$$e_d=R{i}_d+L\frac{d{i}_d}{dt}-\omega L{i}_q+{\nu }_d$$

(20)

$$e_q=R{i}_q+L\frac{d{i}_q}{dt}+\omega L{i}_q+{\nu }_q$$

(21)

$$\frac{d{i}_d}{dt}=-\frac{R}{L}{i}_d+\omega i_q-\frac{{\nu }_d}{L}+\frac{e_d}{L}$$

(22)

$$\frac{d{i}_q}{dt}=-\frac{R}{L}{i}_q-\omega i_d-\frac{{\nu }_q}{L}+\frac{e_q}{L}$$

(23)

where $e_d$ & $e_q$ are the grid voltages in d-q frame; R, L are the resistance and inductance of the transmission line; $i_d$ & $i_q$ are the inverter output currents in d-q frame; $i_d^{*}$ & $i_q^{*}$ are the inverter output reference currents in d-q frame; $\omega$ is the angular frequency in rad/s; ${\nu }_d$ & ${\nu }_q$ are the inverter output voltages in d-q frame.

The state space model of dq reference voltage equations by replacing the control signal values from Equations (24)–(26).

$$\left[\begin{array}{c}{\nu }_d^{*}\\ {\nu }_q^{*}\end{array}\right]=\left[\begin{array}{cc}-k_p& -\omega L\\ -\omega L& -k_p\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{cc}{k}_p& 0\\ 0& k_p\end{array}\right]\left[\begin{array}{c}{i}_d^{*}\\ i_q^{*}\end{array}\right]+\left[\begin{array}{cc}{k}_i& 0\\ 0& k_i\end{array}\right]\left[\begin{array}{c}{X}_d\\ X_q\end{array}\right]+\left[\begin{array}{c}{e}_d\\ e_q\end{array}\right]$$

(24)

$$\frac{d{x}_d}{dt}=i_d^{*}-i_d$$

(25)

$$\frac{d{x}_q}{dt}=i_q^{*}-i_q$$

(26)

4.2. Outer Control Loop for Voltage Regulation

The outer loop control is employed for the PQ control which is based on the instantaneous power [37]. In the synchronous dq frame, the inverter active and reactive power equations are given as:

$$P=\frac{3}{2}(E_d{i}_d+E_q{i}_q)$$

(27)

$$Q=\frac{3}{2}(E_q{i}_d-E_d{i}_q)$$

(28)

When the d axis of is aligned with the load voltage by PLL, then q axis grid voltage is zero ($E_q$ = 0). Then the current reference for controlling the active and reactive powers in dq axis can be calculated as in Equations (29) and (30):

$$i_d^{*}=\frac{2}{3E_d}{P}^{*}$$

(29)

$$i_q^{*}=-\frac{2}{3E_d}{Q}^{*}$$

(30)

The converter control can also be done by regulating the dc link voltage. This ensures that the power extracted from all sources at DC bus can be delivered to the AC load and also ensure that the dc link voltage is higher than the peak voltage of grid for grid connected applications. DC link voltage has to be fixed slightly higher than the minimum required dc voltage to allow the current controllability and to avoid the over modulation. DC link voltage control is chosen for the outer control loop to generate reference d axis current for the inner control loop. In this work, the outer voltage control loop in the proposed HMG is achieved by the ILC. The d axis reference current has been obtained using the dc link voltage error as in Equation (31) and the q axis reference current has been obtained using Equation (32) depending on the inverter or bidirectional operation.

$$i_{d(i+1)}^{*}(z)=\beta (1-\sqrt{\alpha })i_{d(i)}^{*}(z)+k\varphi (z)[V_{dc}^{*}(z)-V_{dc}(z)]$$

(31)

$$i_{q(i+1)}^{*}(z)=\beta (1-\sqrt{\alpha })i_{q(i)}^{*}(z)+k\varphi (z)[E_{abc}^{*}(z)-E_{abc}(z)]$$

(32)

In the next section, the results and the inferences have been discussed.

5. Results and Discussion

The Aichi Micro grid test system- Building 12 has been modeled in MATLAB/SIMULINK platform with the components like solar, wind, battery, AC load, DC load, grid, diesel generator and their converters. The block diagram of Aichi Micro grid (AMG) is shown in Figure 16 and

Table 1. System specifications of the Aichi microgrid test system Building 12.

Components	Quantity	Rating
Solar system	1	10 kW
Wind Generator 1	1	10 kW
Wind Generator 2	1	2 kW
Bi-directional Converter	1	50 kVA
Battery	1	97 kWh
DC-DC converter	2	10 kW
DC-DC converter	1	2 kW
Inverter	2	10 kW
Inverter	1	2 kW
DC Voltage		220 V
AC Voltage		415 V

presents the system specifications of AMG.

The system is being operated as AC/DC system as shown in Figure 17. As mentioned earlier, the AC system has the power flow from the solar, wind turbines, inverters to the AC bus. From the AC bus, the voltage is being converted to DC voltage using bidirectional converter and connected to the DC bus, battery and DC loads. In DC system, the power flows from solar, wind system, DC-DC converters to DC bus. Battery and DC loads are getting power from DC bus. In grid connected mode of operation, the power flows from Grid to AC bus which meets AC loads, converted into DC voltage through bidirectional converter supplying power to DC loads and battery.

Table 2. AC load connection details.

Time in s	Real Power in kW	Reactive Power in VAR
0.0–0.2	0	0
0.2–0.6	5	0
0.6–1.0	7	0
1.0–1.3	0	0
1.3–1.5	8	500
1.5–1.75	13	500
1.75–2.0	13.5	1500

and

Table 3. DC load connection details.

Time in s	Real Power in kW
0.0–0.5	10
0.5–1.0	15
1.0–2.0	25

provides the information about ratings of the AC loads and DC loads and its duration.

Table 4. AC load connection Timings.

Loads	Ratings	Connection Time (sec) c-Closed, o-Opened
Load1	5 kW	0.2(c)-1(o)-1.3(c)
Load2	2 kW	0.6(c)-1(o)-1.3(c)
Load3	1 kW & 500 VAR	1.3(c)
Load4	5 kW	1.5(c)
Load5	0.5 kW & 1000 VAR	1.75(c)

presents the variable AC load details and

Table 5. Modes of operation with power from Various sources in DC bus system.

Mode	Time in s	Sources
Autonomous	0.0–0.5	Solar
	0.5–1.0	Solar + Wind Generator 1
	1.0–1.5	Solar + Wind Generator 1 + Wind Generator 2
Grid Connected	1.5–1.75	Diesel Generator
	1.75–2.0	Diesel Generator + Utility Grid + Battery

and

Table 6. Modes of operation with power from Various sources in AC bus system.

Mode	Time in s	Sources
Autonomous	0.0–0.2	No sources
	0.2–0.6	Solar
	0.6–1.0	Solar + Wind Generator 1
	1.0–1.2	No sources
	1.2–1.3	Wind Generator 2
	1.3–1.5	Solar + Wind Generator 1 + Wind Generator 2
Grid Connected	1.5–1.75	Diesel Generator
	1.75–2.0	Diesel Generator + Utility Grid + Battery

gives the modes of operation and the available system load duration.

Primary or local level control of distributed sources is achieved with dedicated FLC ’s on solar, wind turbine 1, wind turbine 2 and battery. This control ensures the constant and stable operation of the DC bus voltage though variation in the input parameters of solar and wind system.

Secondary or master level control is achieved with the proposed control strategy as described in Figure 15. In the proposed microgrid system, there are various modes of operation has to be analyzed for the reliable supply of power. DC bus voltage regulation is carried out by the battery and the AC bus voltage regulation & synchronization of AC bus with the grid is monitored and controlled by the IC. The power balance equation of the microgrid can be written as:

$$P_s+P_{w1}+P_{w2}+P_G+P_{DG}=P_{DCload}+P_{ACload}+P_{loss}+P_b$$

(33)

where $P_s$ is the solar power, $P_{w1}$ is the power from wind turbine 1, $P_{w2}$ is the power from wind turbine 2, $P_b$ is the battery power, $P_G$ is the grid power, $P_{DG}$ is the diesel generator power, $P_{loss}$ is the power loss in the system, $P_{DCload}$ is load demand at DC bus, $P_{ACload}$ is the load at AC bus, $P_l$ is the total loads in the system at any point of time. The battery power is considered as positive during charging mode and negative in discharging mode.

The simulation studies have been carried out for various conditions as follows:

(Case 1) Autonomous mode of operation (0–1.5 s)

(Case 2) Transition between Autonomous mode to grid connected mode (At 1.5 s)

(Case 3) Grid connected mode of operation (1.5–2 s)

To realize the practical situation, both sources and loads are considered as variable in the simulation. In Figure 18 and Figure 19, from 0 s to 1.5 s, the system is operating in autonomous mode of operation in which the power is generated only from the solar, wind turbine 1 & 2 in various combinations. From 1.5 s to 1.75 s, the diesel generator is connected to the system to satisfy the load along with the battery charging. From 1.75 s to 2 s, the utility grid has also been connected to the system along with the diesel generator to satisfy the load demand and the battery charging. In autonomous mode, the power is fed from the renewable sources to DC load & AC loads via DC bus and AC bus. The power management has been done with the proposed SPW-ILC for the inverters in efficient manner. The real power generated from solar, wind turbine 1 & 2 in DC and AC system are shown in Figure 18 and Figure 19 respectively. Depending upon the switch closing timings of the sources to the system, the power flow is occurred as mentioned in Table 4 and Table 5.

The power flow through AC bus measurement at Point P is shown in Figure 20. It is perceived that in autonomous mode, the power flow during 0.0–0.2 s & 1.0–1.3 s is zero as mentioned in Table 2. In the remaining timings, the negative power flow and positive power flow indicates that the system works in autonomous mode and grid connected mode respectively. It is being observed that till 0.2 s, no load at AC bus is connected to the system. Only DC load is connected which has been supplied by the renewable sources. Hence in Figure 20, the power flow is observed as zero. From 0.2 s, AC loads are connected to the system which has to be supplied by the renewable sources in this autonomous mode of operation. In grid connected mode from 1.5 s, the power is fed from Diesel generator and from 1.75 s power is from grid and it is observed as positive power flow. In this mode of operation, the battery is in charging condition as shown in Figure 21. Power from diesel generator and current is shown in Figure 22. During various modes of operation, the voltages and currents of AC loads has been measured as shown in Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27 and it is ascertained that the load voltages and currents are maintained constant during their connection period.

The dc bus voltage is measured with the proposed ILC and it is compared with the PI controller and FLC. The inputs to the FLC are the error voltage & change in error. The dc bus voltage is shown in Figure 28 and it is shown that the proposed controller effectively control the bus voltages and maintains the efficient synchronization.

Though FLC is having less rise time, the integral time absolute and squared error is high compared to other controllers. The PI controller is performing well similar to ILC, but when the diesel generator is connected to the microgrid, there is significant deviation in the voltage level. In these aspects, the proposed ILC provides better results, less error, less overshoot and settling time compared to other controllers.

6. Conclusions

A coordinated control and the power management among the distributed sources have been performed with the proposed novel SPW-ILC for Aichi Micro grid system. At source level control, dedicated FLC ’s have been used for the maximum power tracking operation of solar, wind and to maintain the constant DC bus voltage. In system level control, the proposed controller has been implemented to control the IC between DC/AC bus and inverters. The controller acts as voltage regulator to control the DC link voltage and also maintains the power balance condition under variable source and load conditions.Several case studies in autonomous and grid connected mode of operation have been analyzed for the performance of the proposed controller. The results have been compared with PI & FLC and the results show that ILC effectively controls the microgrid by stabilizing the voltage at AC/DC bus with less error;reduced overshoot;synchronizing the microgrid with utility grid; attaining the power balance condition in AC and DC systems. In future work, the hardware setup for the microgird test bed with proposed ILC controller can be developed to validate its performance and superiority in real time scenarios. Additionally, ILC parameters can be tuned using meta heuristic algorithms to obtain better results.