Damage Evolution Mechanisms of Rock Induced by Blasting with the Aid of Empty-Hole Effect
Abstract
:1. Introduction
2. Solution and Algorithm in Blasting Model
2.1. Lagrange, Euler and ALE Algorithms
2.2. Implicit–Explicit Analysis Method
- (1)
- Perform the implicit analysis in ANSYS and apply the in situ stress (static loading) to the numerical model. The ‘entity 185′ type element is used in the implicit analysis. Then, we apply the boundary conditions to the numerical model. Finally, we conduct the numerical calculation of the numerical model.
- (2)
- Convert the implicit analysis in ANSYS into the explicit analysis in LS-DYNA. To generate the in situ stress in the explicit analysis in LS-DYNA, the ‘entity 185′ type elements in ANSYS need to be converted into the ‘entity 164′ element (with 8 nodes) in LS-DYNA. A dynamic relaxation file is generated in the conversion process. The displacements in the dynamic relaxation file are used to generate the in situ stress in the explicit analysis in LS-DYNA.
2.3. Simulation Process
3. Constitutive Model Establishment
3.1. Explosive State Equation
3.2. Tension–Compression Damage Model
3.2.1. Kinematic Hardening Model Based on Plastic Strain Rate
3.2.2. Rock Mass Damage Criterion
3.2.3. Evolution of Damaged Rock Element
- (1)
- The macroscopic rock properties are assumed to be isotropic.
- (2)
- The microscopic rock element obtains Hooke’s law before damage (i.e., linear elastic deformation).
4. Establishment and Validation of Numerical Model
4.1. Model Validation and Calculation Procedure
4.1.1. Experimental Study
4.1.2. Model Validation
4.2. Model Development and Calculation Flowchart
- (1)
- Determine the trial value of stress tensor . . ), where Cijkl is the elastic tangent modulus matrix.
- (2)
- Judge the tensile state or the compressive state of the rock element. If εv > 0, the element is in compression; otherwise, the element is in tension.
- (3)
- Determine the latest damage variables (Dts and Dcs).
- (4)
- If the rock element is in tension, the number of the damaged elements increases by 1 (mts = mts + 1); otherwise, ncs = ncs + 1.
- (5)
- Calculate the trial value of the deviatoric stress tensor based on different stress states (), where is the trial deviatoric stress tensor at n step.
- (6)
- Calculate the equivalent strain rate ().
- (7)
- Judge the plastic yield condition. If F ≤ 0, the material is in the elastic deformation state, the trial value of the stress is true; otherwise, step into Step (9) to determine the stress tensor .
- (8)
- If F > 0, the material is in the plastic deformation state; otherwise, determine the plastic multiplier, and then calculate the updated equivalent plastic strain ; the radial regression of the deviatoric stress to the yield element surface is , where α is the plastic multiplier.
- (9)
- Calculate the stress tensor .
- (10)
- Update the stress damage .
- (11)
- Update the history output and return to Step (1) for the new calculation cycle.
4.3. Numerical Model Establishment
5. Numerical Modeling Results
5.1. Analysis of Stress Wave Evolution
5.1.1. Stress Wave Attenuation
5.1.2. Stress Wave Reflection
5.1.3. Stress Wave Superimposition
5.1.4. Influence of Empty Borehole
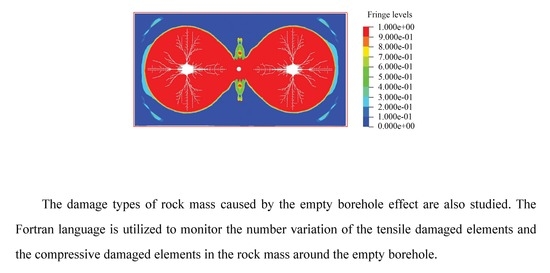
5.2. Damage Evolution around an Empty Borehole with 2 cm Diameter
5.3. Damage Evolution around Empty Boreholes with Different Diameters
6. Conclusions
- (1)
- The empty borehole can significantly enhance the tensile stresses and the stress concentration factors in the rock mass elements nearby the empty borehole. The maximum tensile stress at the monitoring point increases as the distance between the monitoring point and the empty borehole decreases. The stress concentration factor in the rock mass nearby the empty borehole decreases as the angle between the horizontal line and the line connecting the element and the empty borehole centre increases.
- (2)
- The existence of the empty borehole increases the number of the tensile damage elements. The tensile damage dominates the damage of the rock mass around the empty borehole. The incidence compressive stress wave reflects at the empty borehole free surface and is converted into the tensile stress wave. The fracture initiation in the rock mass nearby the empty borehole is dominated by the tensile stress wave.
- (3)
- The damage zone extends as the empty borehole diameter increases, and the rock mass nearby the empty borehole mainly damages in tension. With the increase of the empty borehole diameter, the number of the compressive damaged elements decreases non-linearly, and the number of the tensile damaged elements increases almost linearly. As the empty borehole diameter increases, the ratio of the compressive damaged elements decreases and the ratio of the tensile damaged elements increases.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A, B, R1, R2 and ω | parameters of JWL equation of state |
| Pb | pressure applied to the borehole wall |
| Ei | initial internal energy density of the detonation product |
| c, p | contants of Kinematic Hardening relation |
| β | hardening coefficient |
| Ep | the kinematic hardening modulus |
| Etan | the tangent modulus |
| E0 | Young’s modulus |
| F(σ) | strength function |
| F,F0 | Weibull distribution parameters |
| S | rock strength |
| M | the total number of internal micro units in rock micro element |
| Mf | the number of internal micro units in rock micro element |
| Q(F) | probability density distribution function |
| V | relative volume of the detonation product |
| strain rate | |
| μ | Poisson’s ratio |
| σ1 | maximum principal stress |
| σ3 | minimum principal stress |
| σs | yield stress |
| σts | dynamic tensile strength |
| σcs | dynamic compressive strength |
| Dts | damage parameters of tensile stress |
| Dcs | damage parameters of compressive stress |
| At, Bt | material constants |
| trial stress tensor | |
| , | stress tensor with damage from the previous step |
| stress tensor | |
| G | shear modulus |
| , | deviatoric stress tensor |
| εv | volumetric strain |
| effective plastic strain | |
| volumetric strain increment | |
| effective plastic strain increment | |
| the incremental strain tensor | |
| trial deviatoric stress tensor | |
| total number of element damage with tensile stress at n step | |
| number of element damage with tensile stress at i step | |
| total number of element damage with compressive stress at n step | |
| number of element damage with compressive stress at i step | |
| Ds | damage variable |
| σz | vertical stress |
| σh | horizontal stress |
| σψ | tangential tensile stress |
| σρ | blast-induced radial stress |
References
- Adhikari, G.R.; Babu, A.R.; Balachander, R.; Gupta, R.N. On the application of rock mass quality for blasting in large underground chambers. Tunn. Undergr. Space Technol. 1999, 14, 367–375. [Google Scholar] [CrossRef]
- Wang, F.T.; Tu, S.H.; Yuan, Y.; Feng, Y.F.; Chen, F.; Tu, H.S. Deep-hole pre-split blasting mechanism and its application for controlled roof caving in shallow depth seams. Int. J. Rock Mech. Min. Sci. 2013, 64, 112–121. [Google Scholar] [CrossRef]
- Xu, N.W.; Li, T.B.; Dai, F.; Zhang, R.; Tang, C.A.; Tang, L.X. Microseismic Monit-oring of Strainburst Activities in Deep Tunnels at the Jinping II Hydropower Station, China. Rock Mech. Rock Eng. 2016, 49, 981–1000. [Google Scholar] [CrossRef]
- Yue, Z.W.; Guo, Y.; Wang, X.; Yang, H.B.; Han, T.X. Influence of empty hole shape on direct-ional fracture controlled blasting of rock. Rock Soil Mech. 2016, 37, 376–382. [Google Scholar] [CrossRef]
- Bian, K.F.; Li, H.B.; Liu, Y.Q. Numerical Simulation for the Damping Effect of Empty Holes on Blasting Vibration. Adv. Mater. Res. 2014, 1490–1495. [Google Scholar] [CrossRef]
- Amiri, H.S.; Murthy, V.M.S.R. Optimising blast pulls and controlling blast induced excavation damage zone in tunnelling through varied rock classes. Tunn. Undergr. Space Technol. 2019, 85, 307–318. [Google Scholar] [CrossRef]
- Liu, J.; Guo, X.Q.; Liu, Z.J. Pressure field investigation into oil&gas wellbore during perforating shaped charge explosion. J. Pet. Sci. Eng. 2019, 172, 1235–1247. [Google Scholar]
- Cho, S.H.; Nakamura, Y.; Mohanty, B.; Yang, H.S.; Kaneko, K. Numerical study of fracture plane control in laboratory-scale blasting. Eng. Fract. Mech. 2008, 75, 3966–3984. [Google Scholar] [CrossRef]
- He, C.L.; Yang, Y. Experimental and numerical investigations of dynamic failure process in rock under blast loading. Tunn. Undergr. Space Technol. 2018, 83, 552–564. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical simulation of blasting-induced rock fractures. Int. J. Rock Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Chen, B.B.; Liu, C.Y.; Yang, J.X. Design and Application of Blasting Parameters for Presplitting Hard Roof with the Aid of Empty-Hole Effect. Shock Vib. 2018, 2018, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Taylor, L.M.; Chen, E.P.; Kuszmaul, J.S. Microcrack-induced damage accumulation in brittle rock under dynamic loading. Comput. Method. Appl. Mech. Eng. 1986, 55, 301–320. [Google Scholar] [CrossRef]
- Kuszmaul, J.S. A new constitutive model for fragmentation of rock under dynamic loading. In Proceedings of the 2nd International Symposium on Rock Fragmentation by Blasting, Columbia, SC, USA, 23 August 1987; pp. 412–423. [Google Scholar]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Furlong, J.R.; Alme, M.L.; Rajendran, A.M. Numerical modeling of ceramic penetration experiments. In Proceedings of the Fourth TACOM Armor Coordinating Conference for Light Combat Vehicles, Monterey, CA, USA, 31 March 1988. [Google Scholar]
- Wu, C.; Lu, Y.; Hao, H. Numerical prediction of blast-induced stress wave from large-scale underground explosion. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 93–109. [Google Scholar] [CrossRef]
- Hu, Y.G.; Lu, W.B.; Chen, M.; Yan, P.; Zhou, C.B. Comparison of damage evolution process of high rock slope excavated by different methods. Chin. J. Rock Mech. Eng. 2013, 32, 1176–1184. (In Chinese) [Google Scholar]
- Saharan, M.R.; Mitri, H.S. Numerical procedure for dynamic simulation of discrete fractures due to blasting. Rock Mech. Rock Eng. 2007, 41, 641–670. [Google Scholar] [CrossRef]
- Banadaki, M.D.; Mohanty, B. Numerical simulation of stress wave induced fractures in rock. Int. J. Impact Eng. 2012, 40, 16–25. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, J.; Zhao, J.; Niu, L.L. 2D numerical simulation on excavation damaged zone induced by dynamic stress redistribution. Tunn Undergr. Space Technol. 2014, 43, 315–326. [Google Scholar] [CrossRef]
- Autlo, J. Characterization of the Excavation Disturbance Caused by Boring of the Experimental Full Scale Deposition Holes in the Research Tunnel at Olkiluoto; Posiva-96-09; Posiva: Helsinki, Finland, 1996. [Google Scholar]
- Bäckblom, G.; Martin, C.D. Recent experiments in hard rock to study the excavation response: Implications for the performance of a nuclear waste geological repository. Tunn Undergr. Space Technol. 1999, 14, 377–394. [Google Scholar] [CrossRef]
- Kwon, S.; Lee, C.S.; Cho, S.J.; Choc, S.J.; Jeonb, S.W.; Cho, W.J. An investigation of the excavation damaged zone at the KAERI underground research tunnel. Tunn. Undergr. Space Technol. 2009, 24, 1–13. [Google Scholar] [CrossRef]
- Abuov, M.G.; Aitaliev, S.M.; Ermekov, T.M.; Zhanbyrbaev, N.B.; Kayupov, M.A. Studies of the effect of dynamic processes during explosive break-out upon the roof of mining excavations. Sov. Min. Sci. 1998, 24, 581–590. [Google Scholar] [CrossRef]
- Cai, M. Influence of stress path on tunnel excavation response–numerical tool selection and modeling strategy. Tunn. Undergr. Space Technol. 2008, 23, 618–628. [Google Scholar] [CrossRef]
- Malezhik, M.P.; Malezhik, O.P.; Chernyshenko, I.S. Photoelastic determination of dynamic crack-tip stresses in an anisotropic plate. Int. Appl. Mech. 2006, 42, 574–581. [Google Scholar] [CrossRef]
- Yue, Z.W.; Yang, L.Y.; Wang, Y.B. Experimental Study of Crack Propagation in Polymethyl Methacrylate Material with Double Holes under the Directional Controlled Blasting. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 827–833. [Google Scholar] [CrossRef]
- Asprone, D.; Cadoni, E.; Prota, A.; Manfredi, G. Dynamic behavior of a Mediterranean natural stone under tensile loading. Int. J. Rock Mech. Min. 2009, 46, 514–520. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behavior of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef] [Green Version]
- Hallquist, J.O. LS-DYNA Theory Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- Wang, Y. Analysis of dynamic characteristics of through-wall cracks between 2 boreholes in the directed fracture controlled blasting. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 273–286. [Google Scholar] [CrossRef]
- Jones, N. Structural Aspects of Ship Collisions; Butterworth and Company Publishers Limited: London, UK, 2006; Chapter 11; pp. 308–337. Available online: http://refhub.elsevier.com/S0886-7798(15)30010-9/h0090 (accessed on 31 December 2019).
- Baker, E.L. An Explosives Products Thermodynamic Equation of State Appropriate for Material Acceleration and Overdriven Detonation: Theoretical Background and Fourmulation; Technical Report ARAED-TR-911013, US; Army Armament Research Development and Engineering Center Picatinny: Picatinny Arsenal, NJ, USA, 1991. [CrossRef]
- Kury, J.W.; Horning, H.C.; Lee, E.L.; Mcdonnel, J.L.; Ornellas, D.L.; Finger, M. Metal acceleration by chemical explosives. In Proceedings: Fourth Symposium (International) on Detonation / sponsored by the U. S. Naval Ordnance Laboratory in cooperation with the Office of Naval Research; University of California Libraries: Berkeley, CA, USA, 1965; pp. 3–13. [Google Scholar]
- Sanchidrian, J.A.; Castedo, R.; Lopez, L.M.; Segarra, P.; Santos, A.P. Determination of the JWL constants for ANFO and emulsion explosives from cylinder test data. Cent. Eur. J. Energetic Mater. 2015, 12, 177–194. [Google Scholar]
- Krieg, R.D.; Key, S.W. Implementation of a Time Dependent Plasticity Theory into Structural Computer Programs. Comput. Eng. Asp. 1976, 20, 125–137. [Google Scholar]
- Yang, R.; Bawden, W.F.; Katsabanis, P.D. A new constitutive model for blast damage. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 245–254. [Google Scholar] [CrossRef]
- Xia, X. Study of Damage Characteristics and Safety Threshold of Rock Vibration by Blast. Institute of Rock and Soil Mechanics. Ph.D. Thesis, Chinese Academy of Sciences, Wuhan, China, 2006. [Google Scholar]
- Yang, J.H.; Lu, W.B.; Hu, Y.G.; Chen, M.; Yan, P. Numerical simulation of rock mass damage evolution during deep-buried tunnel excavation by drill and blast. Rock Mech. Rock Eng. 2015, 48, 2045–2059. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Tasaka, Y.; Maejima, T.; Morioka, H.; Minami, M. Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations. Int. J. Rock Mech. Min. Sci. 2004, 41, 833–847. [Google Scholar] [CrossRef]
- Pisarenko, G.S.; Lebedev, A.A. Deformation and Strength of Materials under Complex Stress State; Naukova Dumka: Kiev, Ukraine, 1976. (In Russian) [Google Scholar]
- Krajcinovic, D.; Silva, M.A.G. Statistical aspects of the continuous damage theory. Int. J. Solids Struct. 1982, 18, 551–562. [Google Scholar] [CrossRef]
- Cao, W.G.; Fang, Z.L.; Tang, X.J. A study of statistical constitutive model for soft and damage rocks. Chin. J. Rock Mech. Eng. 1998, 17, 628–633. [Google Scholar]
- Meng, N.K.; Chen, Y.; Bai, J.B.; Wang, X.Y.; Wu, W.D.; Wu, B.W. Numerical simulation of directional fracturing by shaped charge blasting. Energy Sci. Eng. 2020, 1–16. [Google Scholar] [CrossRef]
- Grady, D.E.; Kipp, M.E. Continuum modeling of explosive fracture in oil shale. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1980, 17, 147–157. [Google Scholar] [CrossRef]















| ρ0/(g.cm−3) | D/(m.s−1) | A/(GPa) | B/(GPa) | R1 | R2 | ω | Ei/(GPa) |
|---|---|---|---|---|---|---|---|
| 1000 | 3600 | 214.400 | 0.182 | 4.200 | 0.900 | 0.150 | 4.192 |
| ρ0/(g.cm−3) | C4 | C5 |
|---|---|---|
| 1.29 × 10−3 | 0.04 | 0.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, N.; Bai, J.; Chen, Y.; Wang, X.; Wu, W.; Wu, B.; Liu, S. Damage Evolution Mechanisms of Rock Induced by Blasting with the Aid of Empty-Hole Effect. Energies 2020, 13, 756. https://doi.org/10.3390/en13030756
Meng N, Bai J, Chen Y, Wang X, Wu W, Wu B, Liu S. Damage Evolution Mechanisms of Rock Induced by Blasting with the Aid of Empty-Hole Effect. Energies. 2020; 13(3):756. https://doi.org/10.3390/en13030756
Chicago/Turabian StyleMeng, Ningkang, Jianbiao Bai, Yong Chen, Xiangyu Wang, Wenda Wu, Bowen Wu, and Shuaigang Liu. 2020. "Damage Evolution Mechanisms of Rock Induced by Blasting with the Aid of Empty-Hole Effect" Energies 13, no. 3: 756. https://doi.org/10.3390/en13030756
APA StyleMeng, N., Bai, J., Chen, Y., Wang, X., Wu, W., Wu, B., & Liu, S. (2020). Damage Evolution Mechanisms of Rock Induced by Blasting with the Aid of Empty-Hole Effect. Energies, 13(3), 756. https://doi.org/10.3390/en13030756