Limitations and Characterization of Energy Storage Devices for Harvesting Applications

Abstract

This paper aims to study the limitations and performances of the main energy storage devices commonly used in energy harvesting applications, namely super-capacitors (SC) and lithium polymer (LiPo) batteries. The self-discharge phenomenon is the main limitation to the employment of SCs to store energy for a long time, thus reducing efficiency and autonomy of the energy harvesting system. Therefore, the analysis of self-discharge trends was carried out for three different models of commercial SCs, describing the phenomenon in terms of self-discharge rate and internal resistance. In addition, physical interpretations concerning the self-discharge mechanism based on the experimental data are provided, thus explaining the two super-imposed phenomena featured by distinct time constants. Afterwards, the dependence of self-discharge phenomenon from the charging time duration (namely, SCs charged at 5 V and then kept under charge for one or five hours) was analyzed; by comparing the voltage drop during the self-discharge process, a self-discharge reduction for longer charging durations was obtained and the physical interpretation provided (at best −6.8% after 24 h and −13.4% after 120 h). Finally, self-discharge trends of two commercial 380 mAh LiPo batteries (model LW 752035) were acquired and analyzed; the obtained results show an open circuit voltage reduction of only 0.59% in the first 24 h and just 1.43% after 124 h.

1. Introduction

With the evolution of low power and miniaturized electronic components, the developing of portable electronic devices is increasingly spreading in all human activity fields (communications, medical instruments, goods transport, agriculture, etc.); furthermore, the expansion of energy harvesting technologies is providing new solutions to feed portable, wearable, wireless energetically autonomous systems, so obtaining maintenance-less devices and avoiding the loss of service. A generic harvesting system includes three main sections: (1) a transducer converts the available energy provided by a given source into electric energy; (2) an electronic conditioning section adapts the signal provided by the transducer with the requirements of the electronic load and storage devices [1]. Typically, this section includes an AC/DC converter and a DC/DC regulator, as well as an impedance matching circuit for ensuring the maximum power transfer between transducer and conditioning section; a power management section optimizes the harvesting system operation in order to extend the device energy autonomy. Finally, a storage device (Section 3) stores in a secure and efficient manner the energy provided by the transducers, which is then employed to supply power to a generic electronic load [2,3,4].

In this context, the evolution of energy storage devices (ESD) has to follow the huge development of IoT-oriented devices hand in hand, in order to meet their requirements in terms of energy density, power density, size, weight, etc. [5,6]. Among the different types of ESDs, supercapacitors (SCs) represent an intermediate solution among batteries and traditional capacitors in terms of operation principle, energy, and power density; as is evident from the Ragone plot of Figure 1, SCs have power densities lower than traditional electrolytic and film capacitors, but ensure energy in far higher densities; at the same time, SCs have higher power densities but lower energy densities than Li-ion batteries. However, each application requires a careful ESD choice, according to its technical specifications; in particular, capacitors can ensure an operation cycle on the order of milliseconds or microseconds, with Li-ion batteries also being suitable for applications with operation time in the order of hours. SCs can be used for applications with operation cycles on the order of seconds or minutes; they are widely employed in wireless sensor network (WSN) applications as an alternative to classic capacitors given their higher energy density [7,8]. For instance, in [9] the authors developed a photovoltaic energy harvesting device, conceived as a telemetry node with non-perpetual operation in the indoor environment. The node is equipped with a suitable power management system, also employing the solar panel for the indirect illumination level detection in order to draw power from the backup super-capacitor only during the sleep time intervals during which the system power consumption is less than 25 µW. Toh et al. proposed a self-powered sensor node with a flexible solar panel able to monitor the human body biometric parameters; an ultra-low power circuit efficiently stores the harvested solar energy in a SC for feeding the sensor node [10]. Furthermore, recent technological advances have been made in the stretchable super-capacitors field, SCs that can be now used for health monitoring applications and integrated bio-electronic systems [11]. The SCs are also employed as ESD for realizing charging stations for micro-grid systems and plug-in hybrid electric vehicles (PHEVs); in particular, Kamal et al. proposed a micro-smart grid system equipped with an energy storage hybrid device (with the integration of SCs, battery storage bank and hydrogen fuel cell) that supplies a residential load. The performed tests demonstrated the compliance of the developed system in terms of voltage regulation, frequency deviation and total harmonic distortion (THD) [12].

Therefore, the main goal of this research work is to analyze the self-discharge behavior of the charge storage devices primarily employed in energy harvesting applications, namely SCs and LiPo batteries, varying the device charging time. Through the in-depth analysis of self-discharge time- domain trends obtained from different measurement campaigns carried out on three commercial SC models and two LiPo batteries, some inferences concerning the internal processes causing the self-discharge of energy storage devices are reported. In particular, by analyzing the data related to the temporal trends of SCs’ self-discharge, proper interpretations of the self-discharge phenomenon are provided in the manuscript, directly linked to SCs internal mechanisms, as well as to the charge redistribution, leakage currents and parasitic reactions. In addition, the self-discharge phenomenon is analyzed from the point of view of the equivalent circuit, also describing the effects of the charging time duration in terms of the equivalent circuit’s electrical parameters.

The manuscript is arranged as follows: in the following sub-section, the state of the art concerning the self-discharge phenomenon of SCs and lithium batteries and their related operating issues are reported. The second section describes the devices and methodologies employed to carry out the SCs and LiPo batteries characterization; in Section 3, the main experimental results obtained during the SCs and LiPo batteries characterization are summarized, whereas in Section 4, the analysis of obtained results and the related discussion on them are reported.

State of Art with Respect to the Self-Discharge Phenomenon in SCs and Lithium Batteries

An SC is a charge storage device with greater capacity than that of the common electrolytic capacitor but with lower operating voltages (nominal voltage). They are known by the acronym EDLC (i.e., Electrostatic Double-Layer Capacitors), since the electric field between the electrodes and electrolytes is the main energy storage mechanism; specifically, they do not use a dielectric, but rather a double electric field, which acts as a dielectric material. The SCs are constituted by two porous electrodes (e.g., with activated carbon powder) impregnated with a liquid electrolyte. An ion-conductive separator is placed between the electrodes to prevent short-circuit (Figure 2a). The energy storage is due to the charge accumulation in the ion-absorption layer, represented by the surface of the activated carbon layer of both positive and negative electrodes in contact with the electrolyte (Figure 2b). The electric field between the electrode–electrolyte interfaces gives rise to a double electric layer with a thickness of a few nanometers; at the same time, the porous electrodes, with a large number of grains inside, allow to get a very large activated surface and, thus high capacity values (of the Farad order and more) can be obtained. Since the activated carbon particles are used as electrodes, each carbon layer can be schematized as a single capacitor with C_n capacity. To charge the C_n capacitor, i.e., each activated carbon layer, two resistors are required as described in Figure 2c; through the R₁ resistor, which indicates the resistance between the single grains, the ions move, while through the R_S resistor the layers are charged. The equivalent circuit used for conventional capacitor can also be applied to a super-capacitor as shown in Figure 2d.

R₁, R₂ and R_n are the internal resistances of the activated carbon layers, C₁, C₂ and C_n the electrostatic capacities, while R_L is the insulation resistance of the whole SC device. If a voltage V is applied to the equivalent electrical circuit shown in Figure 2d, then the total current ($i_{tot}$) can be calculated as the sum of the individual currents flowing in each single small capacitor ($C_i$) related to i-th activated carbon layer:

$$i_{tot}= {\displaystyle \sum }_n{i}_n= \frac{V}{R_n}{e}^{\frac{-t}{RnCn}}$$

(1)

The applied voltage can rise up to the so-called “decomposition voltage”, a superior limit value beyond which the current starts flowing between the electrodes, since the electrolyte will begin to decompose, thus causing a greater current flow. The limit operating voltage (nominal voltage) of the SCs depends on the decomposition voltage and varies according to the capacitance value. In Section 4, the SC self-discharge phenomenon will be interpreted in terms of the equivalent circuit reported in Figure 2d, linking the SC’s internal physical mechanisms contributing to the self-discharge with the electrical parameters of the equivalent model.

Several equivalent models have been proposed in the scientific literature for describing the behavior of SCs in power electronic field and energy storage applications [15]. In [16], a dynamic equivalent circuit of a SC, able to reproduce its behavior in time and frequency domain is reported; the equivalent model is based on a Randle circuit rationalized by linearization of the differential equations describing the SC’s internal mechanisms (like charge diffusion, charge drift and conservation). As with the equivalent circuit in Figure 2d, the model in [16] is also constituted by the series of resistor and capacitor in parallel for obtaining multiple time constants. The simulations demonstrated that a wide distribution of the relaxation time constants is needed to properly reproduce the SC’s self-discharge. Furthermore, Yang et al. [17] proposed a different equivalent model for SCs with time-dependent leakage resistance, which includes two branches: the first one represents the immediate discharge effects, whereas the second one reproduces the charge redistribution effect, featured by a higher time constant compared to the first trend. The variable leakage resistance R(t) is employed to model the probability reduction over time of the leakage current inside the SC. In [18], an equivalent model of the SC, constituted by three resistors and two capacitors, was proposed with one of the three resistors being dependent on time to reproduce the charge diffusion. The curve fitting methods were used to determine the time-dependent resistance R(t) from the SC temporal trends. A well-known equivalent model for approximating the SC’s dynamic behavior was reported in [19]; it was constituted by the series of an inductance, a resistor, and complex pore impedance, this last approximated through an RC ladder network with an infinite number of elements. The pore impedance $\underset{\_}{Z_p}\left(j\omega \right)$ models the porosity of the SC electrodes and can be expressed with the following relation:

$$\underset{\_}{Z_p}\left(j\omega \right)=\frac{\tau \times \coth \sqrt{j\omega \tau }}{C\times \sqrt{j\omega \tau }},$$

(2)

where C is the capacitance of the double dielectric layer, whereas $\tau$ is the time constant of a single pore.

SCs’ self-discharging process is the most significant limiting factor that prevents their use for long-term energy storage; the main mechanism contributing to SCs’ self-discharge is the current leakage through the ion-conductive membrane (or separator) placed between the electrodes [20]. Several models have been proposed in the scientific literature for describing this device’s negative feature; in addition to leakage currents, ion redistribution in the electrodes’ pores also causes a long-term variation in the open-circuit voltage after the charging phase. Y Diab et al. proposed an equivalent model to describe SC behavior according to the observed physical phenomena [21]; the developed model includes two RC cells, the main one describes the energy evolution during the charging and discharging phases, while the second one models the internal energy distribution at the end of the charging step, featured by a large time constant. Furthermore, a resistance was added for modeling the current leakage between the two electrodes. In [22], the authors have carefully analyzed the SCs self-discharge phenomenon as function of different parameters such as temperature, charging duration and short-term history. They have demonstrated that the self-discharge rate is inversely proportional to the charging duration. Specifically, three different SC models have been tested, charging them for 15 min or 5 days; the measurement tests demonstrated that the open-circuit voltage remains more stable for the 5 days charged SCs, as well as decreasing rapidly in the first hour, specifically for the 15 min charged SCs. In addition, Miniguano et al. developed a procedure to estimate the parameters of the selected model based on the identification of current profile, to estimate current and voltage waveforms by mean of Matlab simulations of obtained model [23]. After the model selection and optimization method, the parameters are estimated applying the selected optimization solver and, finally, the derived model is verified by comparing application data with the new simulated data.

Referring to Figure 2d, the SC self-discharge is typically characterized by an equivalent resistor R_SD given by the combination of R_L and the internal resistances R_i (i = 1, 2 … n) related to the pore impedances (internal activated carbon layers); therefore, the self-discharge resistance R_SD can be derived by the open-circuit voltage time behavior V(t) by using the following expression:

$$R_{SD}=-\frac{V\left(t\right)}{C\frac{dV\left(t\right)}{dt}},$$

(3)

Considering the discharge law of a parallel RC circuit, with the starting and final voltage values at the SC leaders (indicated with V_start and V_final) on a given time period Δt, an even more accurate estimation of R_SD can be obtained through the following equation:

$$R_{SD}= \frac{\Delta t}{C·ln\frac{V_{start}}{V_{final}}},$$

(4)

Among the various battery types on the market, lithium-ion (Li-Ion) batteries have the best performances; they are the most widespread accumulators regarding the power supply of mobile devices such as phones and laptops, but also electric cars [24], since they present low self-discharge. These battery types are suitable for energy recovery and storage applications, as WSNs, portable and wearable devices, transport applications, etc. [25,26,27]. The lithium is widely used for realizing batteries given its chemical characteristics: besides being the lightest alkaline metal, it is also the least electro-negative one, a feature that guarantees the development of a high contact potential when combined with highly electronegative materials. Moreover, it has a relatively low density, thus allowing the classification of lithium batteries among those with the highest energy density [Wh/Kg] on the market [28]. Furthermore, a Li-ion battery differs from a metallic lithium one, since in a lithium ion cell the lithium is not present in metallic form but some chemical species (i.e., lithium cobalt oxide (LCO), lithium nickel cobalt manganese oxide (NCM), lithium nickel cobalt aluminum oxide (NCA), lithium iron phosphate (LFP), lithium titanium oxide (LTO)) bind with Li+ ions (called lithium intercalation compounds) and then release them if subjected to a typical potential [29]. The ions can migrate from an electrode to another one through the inert electrolyte, generally contained in a spongy separator; the current direction depends on the process in progress (charging or discharging phase). These batteries have gravimetric and volumetric densities (both power and energy density) up to 70% higher than the lead-acid and Ni-MH batteries; also they do not suffer from the memory effect, which instead affects Ni-MH batteries, have a lower self-discharge rate compared to all other batteries [30]; and finally, they can operate over a wide temperature range and support high charging and discharging rates (known as C-rates). However, the Li-ion batteries require a battery management system (BMS) [31], in order to optimize their performances and prevent damages for over-heating or excessive charging [32,33]. In addition, the charging method also affects Li-ion battery performance; for instance, in [34] an advanced charging strategy was proposed for obtaining an optimal constant current constant voltage (CCCV) charging current profile, obtained by optimizing a triple-objective function, namely charging time, energy loss, and temperature increase.

In this context, prognostic methods have been developed to determine the health status of the Li-ion battery applied to electric vehicles (EV), and thus maximizing the battery’s cycle life and charging/discharging efficiency [35]. In [36], the authors carried out a detailed study for highlighting the difference in life cycles relatively to the main materials employed in lithium batteries realization for automotive applications and identifying the knowledge gaps.

An evolution of Li-ion batteries, developed since the 1980s, are lithium polymer (LiPo) accumulators, which include an electrolyte composed of alkaline metals salts solvated into polymers (e.g., polyethylene oxide-PEO) containing hetero-atomic solvents (i.e., without carbon atoms). Most LiPo batteries are based on Li/PEO-Li-salt/IC structure, where IC can be an intercalation compound or an electrode containing a large amount of active intercalation material [37,38]. Similarly to SCs, these batteries are also subject to a self-discharge phenomenon, which reduces the accumulated voltage with a time-varying trend, as a function of different parameters, such as the environmental temperature. Self-discharging is typically ascribable to parasitic reactions of the active material with the electrolyte, thereby causing an active material degradation, due to gas release from the electrolyte oxidation, as well as oxygen losses from LiM(-transition metal) O₂ crystalline structure. SEI formation (solid-electrolyte interphase) at the negative electrode also competes with the Li-ions intercalation leading to a capacity loss of both Li-ion and LiPo batteries [39,40]. Seong et al. demonstrated that a Li-ion cell can suffer from abnormally accelerated self-discharging with thermal exposure (at 60 °C or 80 °C), even a short exposition time intervals [41]. The authors demonstrated that the self-discharging is ascribable to a thin layer of Li₃P, created as consequence of the thermal exposition, that induces a chemical cathode lithiation; in fact, by transmission electron microscopy (TEM) imaging, it is evident the creation of a Li₃P thin film on the charged Li_0.9CoO₂ electrode, just after the thermal treatment, which is then converted to LiP during the self-discharge process [41].

The self-discharging of LiPo batteries, similarly to the Li-ion ones, is lower than 5% over one month; nevertheless, this trend is strongly influenced by the state of charge (SoC), namely if the battery is fully charged, then the self-discharging will be faster, compared to a lower battery SoC (e.g., 40%–60%, as reported in

Table 1. Self-discharge rate of LiPo batteries for the first month [42].

State of Charge	Charge Loss at T = 0 °C for the First Month	Charge Loss at T = 25 °C for the First Month	Charge Loss at T = 60 °C for the First Month
Full charge	6%	20%	35%
40–60% charge	2%	4%	15%

). In [42] a global overview on the self-discharge process of LiPo batteries and their capacity loss is reported; Table 1 summarizes typical values related to the self-discharging rate as function of battery SoC and environmental temperature.

2. Materials and Methods

The super-capacitor models described below are typically used as storage devices in energy harvesting systems and low power portable devices; particularly, three SC models have been characterized, which for the sake of clarity we will indicate below as type A, B, and C. The first model (type-A in Figure 3a) is a Panasonic GC (gold capacitor) SG series SC with 5.5 V nominal voltage, 1 F capacitance, 1 mA maximum discharge current and an operating temperature range from −40 °C to +70 °C (Figure 3a); the second one (type-B in Figure 3b) is a 4 F SC featured by 5.5 V nominal voltage, 31 mA maximum discharge current and an operating temperature range from −25 °C to +70 °C (model GTSE-5R5-474Z/C/V/H manufactured by GTCAP Advanced capacitors Co., Shanghai, China). Both A and B models are “button” shape, having an “H” type package.

The last SC model, produced by the CdA company (Paris, France) and belonging to the CXHP series, has a 2.7 V nominal voltage, 4 F capacitance and a cylindrical shape (type-C in Figure 3c). To compare the self-discharge trends of all charged storage devices in an appropriate way, for comparison uniformity the three SCs were charged to a common voltage of 5 V; for this reason, two 2.7 V type-C SCs were connected in series, thus obtaining an equivalent 2 F SC with a maximum voltage equal to 5.4 V.

Furthermore, a LiPo battery model LW 752035 (manufactured by Celewell Technology Co., Yong Zhou, China) was also tested (Figure 4), in order to evaluate the self-discharge limitation of the two storage devices typology and so determine the best choice as long-time accumulator in energy harvesting applications. The employed LiPo batteries are feature the following technical specifications:

• Nominal capacity: 380 mAh;
• Standard charge: constant current 0.5 C (i.e., it is fully charged with a constant current of 190 mA in 2 h);
• Nominal voltage: 3.7 V (maximum achievable voltage: 4.2 V);
• Maximum constant charging current: 1 C (380 mA);
• Standard discharge: 0.2 C (it supplies the load with a current of 76 mA for 5 h);
• Maximum continuous discharging current: 1.5 C (C-rate).

All the above-described SCs were charged to 5 V, by means of a power supply generator (Haitronic HPS305D, device 1 in Figure 5), and then kept in charge to 5 V for time intervals of one and five hours, respectively, in order to highlight the self-discharge dependence from the charging time duration. A 10 Ω ceramic-housed power resistor (device 2 in Figure 5) was used to limit the current during the charging phase, whereas a portable multimeter (Model GBC KDM-360CTF, manufactured by GBC Electronics, Milan, Italy, device 4 in Figure 5) was used to monitor the SC charging status. This experimental charging process was performed in a closed environment with a temperature of approximately 25 °C.

As already mentioned, two C-type SCs were connected in series, obtaining an equivalent SC, with 2 F capacity and 5.4 V nominal voltage, which was charged to 5 V similarly to the other ones. The voltage values acquired to the SCs series terminals during the self-discharge process are obviously the sum of self-discharge contributions related to each type-C 4 F SC charged to 2.5 V, assuming them to be equal to each other, given the circuital configuration. After the charging phase, the open-circuit voltage of all characterized SCs was monitored by measuring it at more or less regular time intervals with a portable multimeter (manufactured by GBC, model KDM-360CTF) for an observation time interval of 120 h, in order to obtain the self-discharge SCs time-domain trends. This observation time interval was chosen for this study, since within it all the significant effects related to the redistribution of the charge inside the SC’s electrodes can be considered concluded, leaving from then on only the contributions related to charge loss (charge leakage, parasitic reactions, etc.), which decreases with the time, as described in [43]. As mentioned above, the self-discharge phenomenon can be described in terms of the equivalent R_SD resistance by using the relations (3) and (4), on the basis of the SC open-circuit voltage values ($V_{start}$ and $V_{final}$ refer to different time intervals) measured during the self-discharge phase, as detailed in the following section. Additionally, in Section 4, the data acquired for each SC is approximated over the whole observation time interval (120 h) through the sum of two exponential trends featured by different time constants, and the related fitting performances are analyzed.

Subsequently, the self-discharge phenomenon was also investigated in the LiPo batteries, with the same experimental procedure described above, in order to highlight the differences with the SCs behavior. In general, a LiPo battery requires a charging device to prevent damage during the charging phase at constant power; therefore, a LinkMan LK-1008D adapter was used (Figure 6, inset), able to charge only dual cells LiPo batteries simultaneously. The two LW 752035 LiPo batteries (device 4 in Figure 6) are connected in series via interconnecting cables; the common pole of the batteries is connected to the reference input of the adapter (device 3 in Figure 6) via an alligator clip and the positive and negative poles of the series to the respective adapter terminals. The obtained voltage on both under charge batteries was evaluated during the charging process, with a GBC KDM-360CTF portable digital multimeter (device 2 in Figure 6). Also in this case, the LiPo batteries open circuit voltage was monitored over a 120 h long time interval; from these acquired values, the percentage reduction of the battery open-circuit voltage ($\Delta \mathrm{V}/\mathrm{V}$) on two distinct time intervals (24 h and 120 h) was calculated in order to evaluate the LiPo batteries’ self-discharge, and thus the feasibility of their employment in long-term battery-powered portable devices.

3. Results

3.1. Characterization of SC Self-Discharge Phenomenon

In Figure 7, the self-discharge time-domain patterns acquired at more or less regular time intervals are depicted, specifically for two different type-B SCs (indicated as SC_B1 and SC_B2), a type-A SC (indicated as SC_A) and a 2 F equivalent SC obtained by the series of two type-C SCs (indicated as SC_C), all charged at 5 V and then kept under charge for one hour.

As can be seen from the graphs in Figure 7, for the two 4 F SCs (type-B), the self-discharge trend is practically the same over the whole time interval, since their model is the same. Instead, relative to the series of the two type-C cylindrical SCs, despite the capacity halving (2 F compared to 4 F of the other SCs), the self-discharge rate, experimentally observed, is significantly lower than those related to the 4 F type-B SCs, meaning that the 2 F type-C R_SD resistance is much higher than the type-B SCs one, probably due to a much higher manufacturing quality. Furthermore, it should be assumed that the measured self-discharge, related to the series of two 4 F type-C SCs, is the sum of the voltage percentage reduction of the two SCs and, at the same time, each type-C SC was charged to 2.5 V, initial voltage value that heavily affects the self-discharge rate [22]. In addition, the 1F type-A SC shows a higher self-discharge rate respect to the other ones obviously due to its lower capacity, which implies a lower time constant of self-discharge phenomenon and thus a greater reduction of the SC open circuit voltage for a given time interval.

Based on the acquired voltage data plotted in Figure 7, the average self-discharge rates over three contiguous time intervals are calculated: the first one goes from one hour, after the SCs charging phase ends, to six hours later, while the second interval goes from six hours to eighteen hours later and, finally, the third interval goes from eighteen hours to one hundred and twenty hours later (last acquired voltage value over time interval). The calculations performed to determine the average self-discharge rates are the following:

$${\left(\frac{\Delta V}{\Delta t}\right)}_1 =\frac{\left(V_{1,final} – V_{1,start}\right)}{5h}\left[\frac{V}{h}\right],$$

(5)

$${\left(\frac{\Delta V}{\Delta t}\right)}_2 =\frac{\left(V_{2, final} – V_{2,start}\right)}{12h}\left[\frac{V}{h}\right],$$

(6)

$${\left(\frac{\Delta V}{\Delta t}\right)}_3 =\frac{\left(V_{3, final} – V_{3,start}\right)}{102 h}\left[\frac{V}{h}\right],$$

(7)

where ${\left(\frac{\Delta V}{\Delta t}\right)}_i$ is the self-discharge rate for the i-th time interval, as well as $V_{i,start}$ and $V_{i,final}$ (for $i=1, 2, 3$) are the starting and final SC open-circuit voltages for the considered time interval. The thus-calculated self-discharge rates are summarized in

Table 2. Summarizing table with SCs’ self-discharge rates, expressed in mV/h, and self-discharge R_SD resistance calculated for the three considered time intervals (SCs charged at 5 V and then kept under charge for one hour).

	V1,start (V)	V1,final (V)	V2,start (V)	V2,final (V)	V3,start (V)	V3,final (V)	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_1$ [mV/h]	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_2$ [mV/h]	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_3$ [mV/h]	RSD1 [kΩ)]	RSD2 [kΩ]	RSD3 [kΩ]
SC_A	4.46	3.64	3.64	2.87	2.87	1.51	−164.0	−85.6	−14.3	88.6	181.8	571.8
SC_B1	4.73	4.29	4.29	3.90	3.90	3.15	−88.0	−43.3	−7.9	46.1	113.3	429.8
SC_B2	4.71	4.14	4.14	3.74	3.74	3.01	−114.0	−44.4	−7.7	34.9	106.3	422.7
SC_C	4.78	4.49	4.49	4.31	4.31	3.74	−58.0	−20.0	−6.0	143.8	527.9	1294.3

, for the four tested SCs whose self-discharge rates are already plotted in Figure 7, with the limit voltage values of the three considered time intervals; in addition, by means of Equation (3), the average self-discharge R_SD resistance on the three time intervals was calculated, considering the parameter Δt expressed in seconds.

Further tests were carried out by charging the SCs at 5 V and then maintaining them under charge for five hours, in order to analyze the self-discharge behavior as a function of the charging process duration; similarly, a 1F SC (type-A, named SC_A), two 4 F SCs (type-B, named SC_B1, i = 1, 2) and the series of two type-C cylindrical SCs with 2 F equivalent capacity were tested, following the same measurement modalities previously described. In Figure 8, the self-discharge trends of the open-circuit voltage measured at the SC terminals over 120 h’ time span are depicted.

Similarly to the previous experimental measurements, the same three contiguous time intervals were selected, namely a first one from one hour after the SC charging, ending up to six hours later, a second one from six hours to eighteen hours later, and a final one from eighteen hours to one hundred twenty hours later (last acquired voltage value). Therefore, the average self-discharge rates of the acquired trends related to the three time intervals are calculated from the initial and final voltage values, namely $V_{i,final}$, $V_{i, start}$ (for $i=1, 2, 3),$ measured at the SC leads, by using Equations (5)–(7), respectively. The results related to the self-discharge rates and the corresponding self-discharge R_DS resistance in the three considered observation intervals are reported in the following

Table 3. Summarizing table with SCs’ self-discharge rates, expressed in mV/h, and self-discharge R_SD resistance calculated for the three considered time intervals (SCs charged at 5 V and kept under charge for five hours).

	V1,start (V)	V1,final (V)	V2,start (V)	V2,final (V)	V3,start (V)	V3,final (V)	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_1$ [mV/h]	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_2$ [mV/h]	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_3$ [mV/h]	RSD1 [kΩ)]	RSD2 [kΩ]	RSD3 [kΩ]
SC_A	4.55	4.05	4.05	3.37	3.37	2.43	−100.0	−56.7	−9.2	154.6	235.0	1122.9
SC_B1	4.90	4.67	4.67	4.40	4.40	3.87	−46.0	−22.5	−5.2	93.6	181.3	715.2
SC_B2	4.82	4.45	4.45	4.09	4.09	3.40	−74.0	−30.0	−6.8	56.3	128.0	496.8
SC_C	4.92	4.82	4.82	4.69	4.69	4.33	−20.0	−10.8	−3.5	438.3	790.0	2298.9

.

3.2. Characterization of LiPo Batteries’ Self-Discharge Phenomenon

As discussed above, two 380 mAh LiPo batteries (model LW 752035) were also tested, in order to determine their performances in terms of self-discharge. Taking into account the experimentally determined self-discharge rate (6%–10% over each month) already reported in the literature for Li-ion batteries [44], the residual voltage values provided by the tested Li-Po batteries were collected at short time intervals in the first hours after the charging phase end and then more temporally spaced up to the observation interval end (124 h after the charging phase end); in Figure 9, the time-domain trends of the Li-Po batteries open-circuit voltage are shown.

As can be verified from the residual voltage values reported in the temporal graphs of Figure 9, the supply voltage provided by both LiPo batteries decreases by 0.59% in the first 24 h and just 1.43% after just over 5 days (exactly 124 h), meaning that the batteries’ voltage drop is 0.59% in the first day after the charging phase end and only 0.84% over the following four days. Specifically, the absolute variations after the first 24 h and after 124 h from the charging end of the two LiPo batteries are calculated below:

$${\left(\frac{\Delta V}{V}\right)}_{24h} =\frac{\left(4.175 V –4.20 V\right)}{4.20 V}=-0.0059\left(-0.59\%\right),$$

(8)

$${\left(\frac{\Delta V}{V}\right)}_{124h} =\frac{\left(4.14 V– 4.20 V\right)}{4.20 V}=-0.0143 \left(-1.43\%\right),$$

(9)

This result indicates that self-discharge performances of tested LiPo batteries are in accordance with the percentage variations reported in [44]; in fact, given the afore reported temporal trend, the considered LiPo batteries lose only 6.63% in the first month. Furthermore, the obtained results are in agreement with the theoretical model concerning the LiPo batteries’ self-discharge reported in [42].

4. Discussion

In this section, the experimental results are discussed and analyzed in order to highlight the dependence of the self-discharge phenomenon on the different parameters like the initial voltage, charging duration, environmental temperature, as already reported in other related works [21,22]. The aim of this section is also to compare the self-discharge performances of different models of SC and Lipo battery; obviously, the following considerations related to self-discharge behavior will take into account the different technical specifications of the characterized storage devices. Additionally, the comparisons are carried out in terms of R_SD resistance, normalized with respect to the capacitance value, so determining a parameter dependent just from the device manufacturing quality.

From the data reported in Table 2 and Table 3, it can be deduced that, for all considered SC typologies, the self-discharge R_SD resistance is much greater in the last time interval (from the eighteenth hour to the one hundred and twentieth hour) compared to the previous ones (red and green font respectively in Table 2 and Table 3). This observation indicates the presence of two distinct phases in the SCs’ self-discharge: a first short-term behavior covering the first 15–18 h, followed by a long-term one valid for the whole subsequent time, with gradually increasing values of R_SD resistance. The behavior in the initial time interval can be explained with an ions redistribution inside the electrodes’ pores; in fact, at the end of charging phase, the ions aren’t uniformly distributed along the pores depth of each electrode, and thus when the SCs are no longer under charge, the charge will redistribute inside the electrode material causing an initial voltage drop, which does not correspond to any charge loss, as detailed in [22]. This mechanism is in agreement with the equivalent circuit reported in Figure 2d; in fact, for shorter charging processes (up to a few hours) of the SCs, only the opening of the pores is involved in the charge distribution mechanism during the charging phase. Therefore, wanting to find a relationship between this physical behavior to the SC equivalent circuital model shown in Figure 2d, only the first equivalent capacitors (e.g., C₁ and C₂), related to the shallower layers of the electrodes featured by a low internal series resistance (R₁ and R₂, respectively), are charged. In this way, after the end of charging, the charge accumulated on C₁ and C₂ is redistributed to the other equivalent capacitors, related to deeper layers of the electrodes and thus featured by higher internal series resistances, leading to a voltage variation with time constant dependent by the series resistances of the other circuit branches (R_i, for i = 3,…, n).

Instead, the long-term phase, observed after the first 15–18 h, can be attributed to current leakage through the SC separator layer and to parasitic charge transfer mechanisms between electrodes and electrolyte, resulting in an effective charge loss [45]; from the point of view of the equivalent model reported in Figure 2d, these charge leakages are all modeled by means of the R_L insulation resistor placed in parallel to the pores contributions.

As is evident in Figure 8 and Figure 9, the two 4 F SCs (type-B) show similar self-discharge rates, whereas the 1 F one (type-A), given the lower time constant being the capacity value four times lower, has the highest self-discharge rate. With respect to the series of the two type-C SCs, despite the lower equivalent capacity (2 F respect to 4 F), it presents a self-discharge rate lower respect to the other tested devices, although the acquired voltage values provided by SCs series take into account the self-discharge contributions of both 4 F type-C SCs connected in series. In the same way, given that the initial voltage affects the self-discharge rate of SCs [22], it must be taken into account that each type-C SC connected in series was charged at 2.5 V. Specifically, a higher initial voltage of charged SC induces a faster self-discharge rate, since there is a greater accumulation of charge in the electrodes’ pores that will be redistributed when the charging phase ends, thus determining a higher voltage drop; however, this effect can be considered counter-balanced by the voltage reduction doubling related to the self-discharging of SCs connected in series, thus confirming the better manufacturing quality of tested type-C cylindrical capacitors. Likewise, with reference to R_SD resistance featuring the self-discharge trends for the tested SCs (Table 2 and Table 3), taking into account that for the 2 F SC_C storage device the reported R_SD resistance values are related to the sum of two resistors in series; however, the R_SD value of each 4 F type-C SC is greater than those related to the other SCs typologies. Since the self-discharge R_SD resistance is independent of the SC capacitance value, but related to the device manufacturing quality, relative to the characterized storage devices, the 1 F type-A SC is characterized by a higher R_SD resistance with respect to the 4 F type-B SCs (Table 2 and Table 3).

Furthermore,

Table 4. Comparison of self-discharge rate and R_SD resistance values for the characterized SCs relatively to the one hour and five hours under charge cases at 5 V.

		${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_1$ [mV/h]	RSD1 [kΩ)]	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_2$ [mV/h]	RSD2 [kΩ]	${\left(\frac{\mathbf{\Delta }\mathit{V}}{\mathbf{\Delta }\mathit{t}}\right)}_3$ [mV/h]	RSD3 [kΩ)]
5 V charged and then one hour under charge	SC_A	−164.0	88.6	−85.6	181.8	−14.3	571.8
	SC_B1	−88.0	46.1	−43.3	113.3	−7.9	429.8
	SC_B2	−114.0	34.9	−44.4	106.3	−7.7	422.7
	SC_C	−58.0	143.8	−20.0	527.9	−6.0	1294.3
5 V charged and then five hours under charge	SC_A	−100.0	154.6	−56.7	235.0	−9.2	1122.9
	SC_B1	−46.0	93.6	−22.5	181.3	−5.2	715.2
	SC_B2	−74.0	56.3	−30.0	128.0	−6.8	496.8
	SC_C	−20.0	438.3	−10.8	790.0	−3.5	2298.9
Percentage difference	SC_A	−39.0%	74.5%	−33.8%	29.3%	−35.7%	96.4%
	SC_B1	−47.7%	103.0%	−48.0%	60.0%	−34.2%	66.4%
	SC_B2	−35.1%	61.3%	−32.4%	20.4%	−11.7%	17.5%
	SC_C	−65.5%	204.8%	−46.0%	49.65%	−41.6%	77.61%

summarizes the previous results by comparing the obtained values of self-discharge rates and R_SD equivalent resistance (in the three considered time intervals) for the two different experimental cases, i.e., charging the SCs at 5 V and then kept under charge for one hour or five hours. As already highlighted, the self-discharge rate values related to the C-type cylindrical SCs are the smallest (red font in Table 4), although the series equivalent capacitance is only 2 F; even more so, the corresponding R_SD resistance values are the highest by far (green font). Furthermore, the improvement in the case of SCs five hours under-charging after being charged at 5 V is evident for all SCs typologies; in particular, for the type-C SCs, the self-discharge rates are reduced of about 65%, 46% and 41% (for the time intervals 1, 2 and 3, respectively), as well as the R_SD values increase by 204%, 49% and 104%, respectively (reported values in the orange and blue font for the self-discharge rate and R_SD resistance, respectively).

The reduction of self-discharge rate ($\Delta \mathrm{V}/\Delta \mathrm{t}$) with the charge duration (one and five hours under charge at 5 V), as highlighted in Table 4, is due to the better penetration and distribution of the charges in the electrodes’ pores; in fact, when the charging phase ends, a lower voltage drop is obtained on the SC terminals, when SCs are kept under charge for five hours at 5 V, given the lower charge redistribution in the electrodes’ pores respect to the one hour under charge case. In terms of the equivalent circuit reported in Figure 2d, by increasing the charge duration also the secondary equivalent capacitors (namely C₃, C₄ … C_n), featured by higher time constants, are fully or partially charged and therefore, when the supply voltage is removed from the energy storage device, a lower redistribution in the high-index not-completely-charged capacitors is obtained.

Furthermore, for approximating the voltage values acquired over time and related to the different SCs, an exponential fitting function given by the sum of two exponential trends with distinct time constants ($\tau 1, \tau 2$) was considered, as reported in previous research works [22,46]:

$$V\left(t\right)=a\times e^{-\frac{t}{\tau 1}}+b\times e^{-\frac{t}{\tau 2}},$$

(10)

For instance, in Figure 10, exponential fitting curves are reported related to the acquired data for the SCs kept under charge at 5 V for 1 h, whereas in

Table 5. Table with the parameters of the exponential fitting functions for the SCs kept in charge at 5 V for 1 h; the determination coefficient (R²) and root mean square error (RMSE) are also reported.

SC	$\mathit{a}$	$\mathit{\tau }1\left[\mathbf{h}\right]$	$\mathit{b}$	$\mathit{\tau }2\left[\mathbf{h}\right]$	R2	RMSE
SC_A	1.94	7.78	2.84	181.59	0.996	0.083
SC_B1	1.08	8.25	3.82	568.18	0.996	0.044
SC_B2	1.23	7.15	3.67	545.25	0.996	0.044
SC_C	0.58	5.92	4.32	759.87	0.993	0.036

the corresponding fitting parameters ($a, \tau 1,b, \tau 2$ related to Equation (10)) are summarized, along with the determination coefficient (defined as ${{\displaystyle \sum }}_{i=1}^N\frac{{({\widehat{V}}_i-\overline{V})}^2}{{(V_i-\overline{V})}^2}$, R²) and the root mean square error (defined as $\sqrt{{{\displaystyle \sum }}_{i=1}^N{(\widehat{V_i}-V_i)}^2/N,} RMSE$) of each determined approximation.

The data reported in Table 5 confirm the goodness of the double exponential fitting function previously supposed; in fact, the RMSE is lower of 0.085 for all the approximating functions. Also, the presence of the two distinct trends featured by different time constants ($\tau 1$, $\tau 2$) is evident, as previously discussed: the first one with small time constant ($\tau 1$, values in the green font) ascribable to charge redistribution phenomenon, which dominates in the first hours after the charging end, and a second one with much higher time constant values ($\tau 2$, values in the red font) ascribable to the charge loss mechanisms previously discussed.

Finally, a comparison between the open-circuit voltage variations due to self-discharge phenomenon for the most performing tested SCs, namely the type-B SC (SC_B1) and the series of type-C SCs (SC_C), both charged at 5 V for one or five hours, and the LiPo batteries, after 24 and 120 h, is reported in

Table 6. Voltage percentage variations for the most performing tested SCs, kept under charging at 5 V for one and five hours, and for the LiPo batteries.

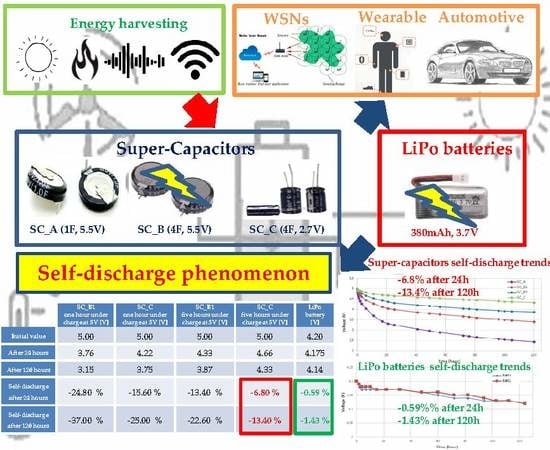
	SC_B1 One Hour Under Charge at 5 V [V]	SC_C One Hour Under Charge at 5 V [V]	SC_B1 Five Hours Under Charge at 5 V [V]	SC_C Five Hours Under Charge at 5 V [V]	LiPo Battery LW 752035 [V]
Initial value	5.00	5.00	5.00	5.00	4.20
After 24 h	3.76	4.22	4.33	4.66	4.175
After 120 h	3.15	3.75	3.87	4.33	4.14
Self-discharge after 24 h	−24.80%	−15.60%	−13.40%	−6.80%	−0.59% 1
Self-discharge after 120 h	−37.00%	−25.00%	−22.60%	−13.40%	−1.43% 1

¹ Values referred to 124 h instead of 120 h.

.

As it can be noted from Table 5, the series of the two type-C cylindrical SCs with 2 F equivalent capacity offers the best performances in terms of self-discharge compared to the other tested SCs model. Finally, the LiPo batteries have a practically negligible voltage loss over a 5-day-long time interval compared to the 2 F type-C SCs behavior, thus resulting, on the basis of the obtained experimental results, the most suitable energy storage device to efficiently power supply energetically autonomous systems for a long time.

5. Conclusions

In this manuscript, a critical analysis is reported with respect to the limitations and observed performances of the main energy storage devices, namely SCs and LiPo batteries, commonly employed for energy harvesting applications. Particularly, the SCs’ self-discharge is the main limitation to their employment as long-term energy storage devices; therefore, a quantitative analysis of the self-discharge performances for three common SC models has been carried out, describing the phenomenon in terms of the commonly used metrics, as self-discharge rate and equivalent R_SD resistance. Based on the analysis of acquired self-discharge time-domain trends, two distinct physical mechanisms with different time constants are evident: a short-term behavior due to the charge redistribution in the electrodes’ pores and a long-term one ascribable to both charge leakages through the SC separator layer and parasitic charges transfer between electrodes and electrolyte. By comparing the voltage drop acquired values as function of time, relatively to the characterized SCs for different charging durations (i.e., one and five hours under charge at 5 V), a significant reduction of the self-discharge rate is obtained for all tested SCs by increasing the duration of charge, a justifiable result with a better charge distribution and penetration in the electrodes pores in case of longer charging time durations. Finally, the self-discharge trends of commercial LiPo batteries (LW 752035 model) were also acquired and analyzed; the obtained results show an open-circuit voltage drop of 0.59% in the first 24 h and only 1.43% after just over 5 days (124 h), an experimental result in agreement with other ones already reported in literature (6–10% for each month) [37].

As a next research step, a more extensive analysis, both in terms of observation time interval and number of tested storage devices, will be performed; in particular, a self-discharge analysis on multiple samples (for instance three) for each model of SC and LiPo battery will be carried out, considering an observation time interval of the order of a month. In this way, the average self-discharge profile and related performances (self-discharge rate and R_SD resistance) for each device model can be determined.