Numerical Simulation of Coherent Structures in the Turbulent Boundary Layer under Different Stability Conditions
Abstract
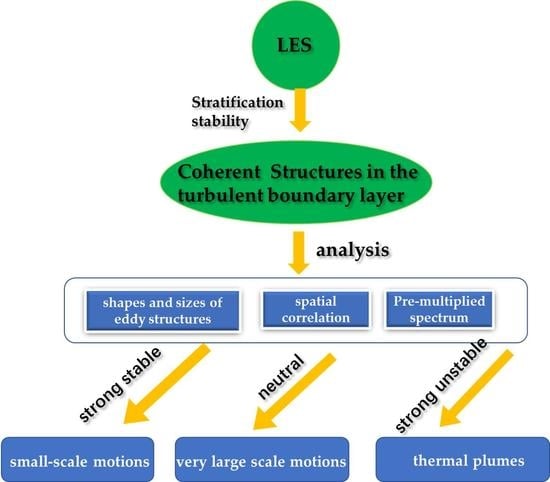
:1. Introduction
2. Simulation Details
3. Validation
4. Results
4.1. Flow Field
4.2. Spatial Correlation Coefficient Field
4.3. Pre-Multiplied Spectral Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 24, 163–187. [Google Scholar]
- Robinson, S.K. Coherent motions in the turbulent boundary-layer. Annu. Rev. Fluid Mech. 1991, 23, 601–639. [Google Scholar] [CrossRef]
- Marusic, I.; Mathis, R.; Hutchins, N. Predictive model for wall-bounded turbulent flow. Science 2010, 329, 193–196. [Google Scholar] [CrossRef] [PubMed]
- Theodorsen, T. Mechanism of turbulence. In Proceedings of the Second Midwestern Conference on Fluid Mechanics, Ohio State University, Columbus, OH, USA, 17–19 March 1952; pp. 1–19. [Google Scholar]
- Kline, S.J.; Reynolds, W.C.; Schraub, F.A.; Runstadl, P.W. Structure of turbulent boundary layers. J. Fluid Mech. 1967, 30, 741–773. [Google Scholar] [CrossRef] [Green Version]
- Adrian, R.J. Hairpin vortex organization in wall turbulence. Phys Fluids 2007, 19, 041301. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T.M. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Kim, K.C.; Adrian, R.J. Very large-scale motion in the outer layer. Phys Fluids 1999, 11, 417–422. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Morrison, J.F. Eddy structure in turbulent boundary layers. Eur. J. Mech. B 2000, 19, 673–694. [Google Scholar] [CrossRef]
- Wang, G.H.; Zheng, X.J. Very large scale motions in the atmospheric surface layer: A field investigation. J. Fluid Mech. 2016, 802, 464–489. [Google Scholar] [CrossRef]
- Adrian, R.J.; Meinhart, C.D.; Tomkins, C.D. Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 2000, 422, 1–54. [Google Scholar] [CrossRef] [Green Version]
- Guala, M.; Hommema, S.E.; Adrian, R.J. Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 2006, 554, 521–542. [Google Scholar] [CrossRef]
- Balakumar, B.J.; Adrian, R.J. Large-and very-large-scale motions in channel and boundary-layer flows. Philos. Trans. R. Soc. Lond. A 2007, 365, 665–681. [Google Scholar] [CrossRef] [PubMed]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic: Dodrecht, The Netherlands, 1988. [Google Scholar]
- Arya, S.P. Introduction to Micrometeorology; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- Kumar, V.; Kleissl, J.; Meneveau, C.; Parlange, M.B. Large-eddy simulation of a diurnal cycle of the atmospheric boundary layer: Atmospheric stability and scaling issues. Water Resour. Res. 2006, 42, 650–664. [Google Scholar] [CrossRef] [Green Version]
- Park, S.B.; Baik, J.J. A large-eddy simulation study of thermal effects on turbulence coherent structures in and above a building array. J. Appl. Meteorol. Climatol. 2013, 52, 1348–1365. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E. Coherent structures and the dissimilarity of turbulent transport of momentum and scalars in the unstable atmospheric surface layer. Bound. Layer Meteorol. 2011, 140, 243–262. [Google Scholar] [CrossRef]
- Basu, S.; Porté-Agel, F. Large-eddy simulation of stably stratified atmospheric boundary layer turbulence: A scale-dependent dynamic modeling approach. J. Atmos. Sci. 2005, 63, 2074–2091. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.N.; Porté-Agel, F. Large-eddy simulation of very-large-scale motions in the neutrally stratified atmospheric boundary layer. Bound. Layer Meteorol. 2015, 155, 397–416. [Google Scholar] [CrossRef] [Green Version]
- Mason, P.J.; Sykes, R.I. A two-dimensional numerical study of horizontal roll vortices in the neutral atmospheric boundary-layer. Q. J. R. Meteorol. Soc. 1980, 106, 351–366. [Google Scholar] [CrossRef]
- Etling, D.; Brown, R.A. Roll vortices in the planetary boundary-layer—A review. Bound. Layer Meteorol. 1993, 65, 215–248. [Google Scholar] [CrossRef]
- Khanna, S.; Brasseur, J.G. Three-dimensional buoyancy-and shear-induced local structure of the atmospheric boundary layer. J. Atmos. Sci. 1998, 55, 710–743. [Google Scholar] [CrossRef]
- Boppe, R.S.; Neu, W.L.; Shuai, H. Large-scale motions in the marine atmospheric surface layer. Bound. Layer Meteorol. 1999, 92, 165–183. [Google Scholar] [CrossRef]
- Hommema, S.E.; Adrian, R.J. Packet structure of surface eddies in the atmospheric boundary layer. Bound. Layer Meteorol. 2003, 106, 147–170. [Google Scholar] [CrossRef]
- Carper, M.A.; Porté-Agel, F. The role of coherent structures in subfilter-scale dissipation of turbulence measured in the atmospheric surface layer. J. Turbul. 2004, 5, 32. [Google Scholar] [CrossRef] [Green Version]
- Chauhan, K.; Hutchins, N.; Monty, J.; Marusic, I. Structure Inclination Angles in the Convective Atmospheric Surface Layer. Bound. Layer Meteorol. 2013, 147, 41–50. [Google Scholar] [CrossRef]
- Salesky, S.T.; Anderson, W. Buoyancy effects on large-scale motions in convective atmospheric boundary layers: Implications for modulation of near-wall processes. J. Fluid Mech. 2018, 856, 135–168. [Google Scholar] [CrossRef]
- Cortese, T.; Balachandar, S. Vortical nature of thermal plumes in turbulent convection. Phys. Fluids 1993, 5, 3226–3232. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Xia, K.Q. Plume statistics in thermal turbulence: Mixing of an active scalar. Phys. Rev. Lett. 2002, 89, 184502. [Google Scholar] [CrossRef] [Green Version]
- Mahrt, L. Stratified atmospheric boundary layers and breakdown of models. Theor. Comput. Fluid Dyn. 1998, 11, 263–279. [Google Scholar] [CrossRef]
- Monin, A.S. Atmospheric boundary layer. Annu. Rev. Fluid Mech. 1970, 2, 225. [Google Scholar] [CrossRef]
- Derbyshire, S.H. Stable boundary-layer modelling: Established approaches and beyond. Bound. Layer Meteorol. 1999, 90, 423–446. [Google Scholar] [CrossRef]
- Holtslag, A.A.M. GABLS Initiates Intercomparison for Stable Boundary Layer Case; GEWEX News, No. 13.; International GEWEX Project Office: Silver Spring, MD, USA, 2003; pp. 7–8. [Google Scholar]
- Hunt, J.C.R.; Shutts, G.J.; Derbyshire, S.H. Stably stratified flows in meteorology. Dyn. Atmos. Oceans 1996, 23, 63–79. [Google Scholar] [CrossRef]
- Deardorff, J.W. Theoretical expression for the countergradient vertical heat flux. J. Geophys. Res. 1972, 77, 5900–5904. [Google Scholar] [CrossRef]
- Deardorff, J.W. Three-dimensional numerical study of turbulence in an entraining mixed layer. Bound. Layer Meteorol. 1974, 7, 199–226. [Google Scholar] [CrossRef]
- Moeng, C.H. A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Moeng, C.H. A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Bound. Layer Meteorol. 1994, 71, 247–276. [Google Scholar] [CrossRef] [Green Version]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A scale-dependent dynamic model for large-eddy simulations: Application to a neutral atmospheric boundary layer. J. Fluid Mech. 2000, 415, 261–284. [Google Scholar] [CrossRef] [Green Version]
- Beare, R.J.; Macvean, M.K.; Holtslag, A.A.M.; Cuxart, J.; Esau, I.; Golaz, J.C.; Jimenez, M.A.; Khairoutdinov, M.; Kosovic, B.; Lewellen, D.; et al. An intercomparison of large-eddy simulations of the stable boundary layer. Bound. Layer Meteorol. 2006, 118, 247–272. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, H.; Schumann, U. Coherent structure of the convective boundary layer derived from large-eddy simulations. J. Fluid Mech. 1989, 200, 511–562. [Google Scholar] [CrossRef] [Green Version]
- Nieuwstadt, F.T.M.; Mason, P.J.; Moeng, C.H.; Schumann, U. Large-eddy simulation of the convective boundary layer: A comparison of four computer codes. In Turbulent Shear Flows 8; Durst, F., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 343–367. [Google Scholar]
- Churchfield, M.J.; Moriarty, P.J.; Vijayakumar, G.; Brasseur, J. Wind Energy-Related Atmospheric Boundary-Layer Large-Eddy Simulation Using OpenFOAM; NREL/CP-500-48905; National Renewable Energy Lab.: Golden, CO, USA, 2010.
- Andren, H. Effects of Habitat Fragmentation on Birds and Mammals in Landscapes with Different Proportions of Suitable Habitat: A Review. Oikos 1994, 71, 355–366. [Google Scholar] [CrossRef] [Green Version]
- Flores, O.; Riley, J.J. Analysis of turbulence collapse in the stably stratified surface layer using direct numerical simulation. Bound. Layer Meteorol. 2011, 139, 241–259. [Google Scholar] [CrossRef]
- Mason, P.J.; Derbyshire, S.H. Large-eddy simulation of the stably stratified atmospheric boundary layer. Bound. Layer Meteorol. 1990, 53, 117–162. [Google Scholar] [CrossRef]
- Brown, A.; Derbyshire, S.H.; Mason, P.J. Large-eddy simulation of stable atmospheric boundary layers with a revised stochastic subgrid model. Q. J. R. Meteorol. Soc. 1994, 120, 1485–1512. [Google Scholar] [CrossRef]
- Saiki, E.M.; Moeng, C.H.; Sullivan, P.P. Large-eddy simulation of the stably stratified planetary boundary layer. Bound. Layer Meteorol. 2000, 95, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Churchfield, M.J.; Sang, L.; Moriarty, P.J. Adding Complex Terrain and Stable Atmospheric Condition Capability to the OpenFOAM-Based Flow Solver of the Simulator for on/Offshore wind Farm Applications (SOWFA); National Renewable Energy Lab.: Golden, CO, USA, 2013; Volume 2.
- Ren, H.; Laima, S.; Li, H. Numerical study of amplitude modulation in the atmospheric boundary layer at very high Reynolds number. AIP Adv. 2019, 9, 105112. [Google Scholar] [CrossRef]
- Schumann, U. Subgrid-scale model for finite-difference simulations of turbulent flow in plane channels and annuli. J. Comput. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef] [Green Version]
- Yoshizawa, A.; Horiuti, K. A statistically-derived subgrid-scale kinetic energy model for the large-eddy simulation of turbulent flows. J. Phys. Soc. Jpn. 1985, 54, 2834–2839. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.H.; Choi, J.; Sung, H.J. Spatial organization of large- and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 2014, 749, 818–840. [Google Scholar] [CrossRef]
- Ren, H.; Laima, S.; Li, H. Numerical Investigation of Very-Large-Scale Motions in a Turbulent Boundary Layer for Different Roughness. Energies 2020, 13, 659. [Google Scholar] [CrossRef] [Green Version]
- Wyngaard, J.C.; Cote, O.R. Cospectral similarity in the atmospheric surface layer. Q. J. R. Meteorol. Soc. 1972, 98, 590–603. [Google Scholar] [CrossRef]
- Zhang, H.S.; Chen, J.Y.; Zhang, A.C.; Wang, J.M.; Mitsuta, Y. An experiment and the results on flux-gradient relationships in the atmospheric surface over Gobi Desert Surface. In Proceedings of the International Symposium on HEIFE, Kyoto, Japan, 1–5 March 1993; Volume IV-12, pp. 349–362. [Google Scholar]
- Zhang, H.; Chen, J.Y.; Park, S.U. Turbulence structure in unstable conditions over various surfaces. Bound. Layer Meteorol. 2001, 100, 243–261. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Tennekes, H.; Lenschow, D.H.; Wyngaard, J.C. The characteristics of turbulent velocity components in the surface layer under convective conditions. Bound. Layer Meteorol. 1977, 11, 355–361. [Google Scholar] [CrossRef]
- Bowne, N.E.; Ball, J.T. Observational comparison of rural and urban boundary-layer turbulence. J. Appl. Meteorol. 1970, 9, 862–873. [Google Scholar] [CrossRef] [Green Version]
- Counihan, J. Adiabatic atmospheric boundary layers: A review and analysis of data from the period 1880–1972. Atmos. Environ. 1975, 19, 871–905. [Google Scholar] [CrossRef]
- Steyn, D.G. Turbulence in an unstable surface layer over suburban terrain. Bound. Layer Meteorol. 1982, 22, 183–191. [Google Scholar] [CrossRef]
- Rotach, M.W. Turbulence Within and Above an Urban Canopy; ETH: Zurich, Switzerland, 1991. [Google Scholar]
- Roth, M. urbulent transfer relationships over an urban surface. II: Integral statistics. Q. J. R. Meteorol. Soc. 1993, 119, 1105–1120. [Google Scholar] [CrossRef]
- Lee, J.H.; Sung, H.J. Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 2011, 673, 80–120. [Google Scholar] [CrossRef]
- Dennis, D.J.C.; Nickels, T.B. Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 2011, 673, 180–217. [Google Scholar] [CrossRef]
- Dennis, D.J.C.; Nickels, T.B. Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 2011, 673, 218–244. [Google Scholar] [CrossRef]
- Baltzer, J.R.; Adrian, R.J.; Wu, X. Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 2013, 720, 236–279. [Google Scholar] [CrossRef]
- Christensen, K.T.; Wu, Y. Characteristics of vortex organization in the outer layer of wall turbulence. In Proceedings of the Fourth International Symposium on Turbulence and Shear Flow Phenomena, Williamsburg, VA, USA, 27–29 June 2005; Volume 3, pp. 1025–1030. [Google Scholar]
- Volino, R.J.; Schultz, M.P.; Flack, K.A. Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 2007, 592, 263–293. [Google Scholar] [CrossRef]
- Hutchins, N.; Marusic, I. Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 2007, 579, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Mathis, R.; Hutchins, N.; Marusic, I. Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 2009, 628, 311–337. [Google Scholar] [CrossRef] [Green Version]
- Balasubramaniam, B.J. Nature of turbulence in wall-bounded flows. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2005. [Google Scholar]












© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laima, S.; Ren, H.; Li, H.; Ou, J. Numerical Simulation of Coherent Structures in the Turbulent Boundary Layer under Different Stability Conditions. Energies 2020, 13, 1068. https://doi.org/10.3390/en13051068
Laima S, Ren H, Li H, Ou J. Numerical Simulation of Coherent Structures in the Turbulent Boundary Layer under Different Stability Conditions. Energies. 2020; 13(5):1068. https://doi.org/10.3390/en13051068
Chicago/Turabian StyleLaima, Shujin, Hehe Ren, Hui Li, and Jinping Ou. 2020. "Numerical Simulation of Coherent Structures in the Turbulent Boundary Layer under Different Stability Conditions" Energies 13, no. 5: 1068. https://doi.org/10.3390/en13051068
APA StyleLaima, S., Ren, H., Li, H., & Ou, J. (2020). Numerical Simulation of Coherent Structures in the Turbulent Boundary Layer under Different Stability Conditions. Energies, 13(5), 1068. https://doi.org/10.3390/en13051068