Modelling the Disaggregated Demand for Electricity in Residential Buildings Using Artificial Neural Networks (Deep Learning Approach) †
Abstract
:1. Introduction
- the application of data with a relatively low sampling rate of 1/600 Hz to model the disaggregated demand for electricity
- the use of different types of ANNs with real and apparent power, as well as selected time and data variables
- the use of the difference between apparent and real power as an input variable in an ANN model.
2. Methodology
2.1. Multilayer Perceptron
2.2. Deep Neural Networks
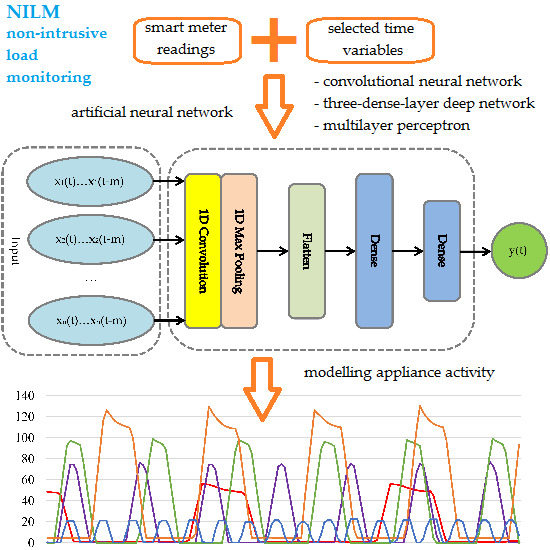
Convolutional Neural Network
2.3. Neural Networks Structure in Modelling Two-State Appliances Activity
2.4. Pre-Assumed Networks Structure and Parameters
2.5. Selection and Preparation of Input and Output Variables of Models
2.6. Performance Metrics
3. Results
4. Discussion
5. Conclusions and Future Work
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Shi, Y.; Zhang, B. Modeling and optimization of complex building energy systems with deep neural networks. Conf. Signals Syst. Comput. 2017, 1368–1373. [Google Scholar]
- Eurostat. Energy consumption and Use by Households. Available online: https://ec.europa.eu/eurostat/web/products-eurostat-news/-/DDN-20190620-1 (accessed on 10 October 2018).
- Liu, B.; Luan, W.; Yu, Y. Dynamic time warping based non-intrusive load transient identification. Appl. Energy 2017, 195, 634–645. [Google Scholar]
- Cominola, A.; Giuliani, M.; Piga, D.; Castelletti, A.; Rizzoli, A. A Hybrid Signature-based Iterative Disaggregation algorithm for Non-Intrusive Load Monitoring. Appl. Energy 2017, 185, 331–344. [Google Scholar] [CrossRef]
- Figueiredo, M.; De Almeida, A.M.; Ribeiro, B. Home electrical signal disaggregation for non-intrusive load monitoring (NILM) systems. Neurocomputing 2012, 96, 66–73. [Google Scholar] [CrossRef]
- Xu, F.; Huang, B.; Cun, X.; Wang, F.; Yuan, H.; Lai, L.L.; Vaccaro, A. Classifier economics of Semi-Intrusive Load Monitoring. Int. J. Electr. Power Energy Syst. 2018, 103, 224–232. [Google Scholar] [CrossRef]
- Yu, J.; Gao, Y.; Wu, Y.; Jiao, D.; Su, C.; Wu, X. Non-Intrusive Load Disaggregation by Linear Classifier Group Considering Multi-Feature Integration. Appl. Sci. 2019, 9, 3558. [Google Scholar] [CrossRef] [Green Version]
- Biansoongnern, S.; Plungklang, B. Non-Intrusive Appliances Load Monitoring (NILM) for Energy Conservation in Household with Low Sampling Rate. Procedia Comput. Sci. 2016, 86, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Akintayo, A.; Jiang, Z.; Henze, G.P.; Sarkar, S. Multivariate exploration of non-intrusive load monitoring via spatiotemporal pattern network. Appl. Energy 2018, 211, 1106–1122. [Google Scholar] [CrossRef]
- Henriet, S.; Şimşekli, U.; Fuentes, B.; Richard, G. A generative model for non-Intrusive load monitoring in commercial buildings. Energy Build. 2018, 177, 268–278. [Google Scholar] [CrossRef] [Green Version]
- Rashid, H.; Singh, P.; Stankovic, V.; Stankovic, L. Can non-intrusive load monitoring be used for identifying an appliance’s anomalous behaviour? Appl. Energy 2019, 238, 796–805. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.S.; Agbossou, K.; Kelouwani, S.; Cardenas, A. Non-intrusive load monitoring through home energy management systems: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 1266–1274. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W.; Kelly, J. Metadata for Energy Disaggregation. In Proceedings of the 2014 IEEE 38th International Computer Software and Applications Conference Workshops; Institute of Electrical and Electronics Engineers (IEEE), Västerås, Sweden, 21–25 July 2014; pp. 578–583. [Google Scholar]
- Hart, G.W. Nonintrusive Appliance Load Data Acquisition Method. In MIT Energy Laboratory Technical Report; MIT: Cambridge, MA, USA, 1984. [Google Scholar]
- Kolter, J.Z.; Johnson, M.J. REDD: A public data set for energy disaggregation research. In Proceedings of the SustKDD Workshop of Data Mining Applications in Sustainability, San Diego, CA, USA, 21 August 2011. [Google Scholar]
- Bonfigli, R.; Principi, E.; Fagiani, M.; Severini, M.; Squartini, S.; Piazza, F. Non-intrusive load monitoring by using active and reactive power in additive Factorial Hidden Markov Models. Appl. Energy 2017, 208, 1590–1607. [Google Scholar] [CrossRef]
- Azaza, M.; Wallin, F. Finite State Machine Household’s Appliances Models for Non-intrusive Energy Estimation. Energy Procedia 2017, 105, 2157–2162. [Google Scholar] [CrossRef]
- Tomkins, S.; Pujara, J.; Getoor, L. Disambiguating Energy Disaggregation: A Collective Probabilistic Approach. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2857–2863. [Google Scholar]
- Schirmer, P.A.; Mporas, I.; Paraskevas, M. Energy Disaggregation Using Elastic Matching Algorithms. Entropy 2020, 22, 71. [Google Scholar] [CrossRef] [Green Version]
- Penha, D.D.P.; Castro, A.R.G. Home Appliance Identification for Nilm Systems Based on Deep Neural Networks. Int. J. Artif. Intell. Appl. 2018, 9, 69–80. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, F. Concatenate Convolutional Neural Networks for Non-Intrusive Load Monitoring across Complex Background. Energies 2019, 12, 1572. [Google Scholar] [CrossRef] [Green Version]
- Beckel, C.; Kleiminger, W.; Cicchetti, R.; Staake, T.; Santini, S. The ECO data set and the performance of non-intrusive load monitoring algorithms. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings—BuildSys, Memphis, TN, USA, 5–6 November 2014; pp. 80–89. [Google Scholar]
- Liu, C.; Jiang, Z.; Akintayo, A.; Henze, G.P.; Sarkar, S. Building Energy Disaggregation using Spatiotemporal Pattern Network. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 1052–1057. [Google Scholar]
- Dong, M.; Meira, P.C.; Xu, W.; Chung, C.Y. Non-Intrusive Signature Extraction for Major Residential Loads. IEEE Trans. Smart Grid 2013, 4, 1421–1430. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Boil. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [Green Version]
- Ivakhnenko, A.G.; Lapa, V.G. Cybernetic Predicting Devices; CCM Information Corp.: New York, NY, USA, 1965. [Google Scholar]
- Zhang, C.-L.; Wu, J. Improving CNN linear layers with power mean non-linearity. Pattern Recognit. 2019, 89, 12–21. [Google Scholar] [CrossRef]
- Debayle, J.; Hatami, N.; Gavet, Y. Classification of time-series images using deep convolutional neural networks. In Proceedings of the Tenth International Conference on Machine Vision (ICMV 2017), Vienna, Austria, 13–15 November 2017; p. 106960. [Google Scholar]
- Wang, K.; Li, K.; Zhou, L.-Q.; Hu, Y.; Cheng, Z.; Liu, J.; Chen, C. Multiple convolutional neural networks for multivariate time series prediction. Neurocomputing 2019, 360, 107–119. [Google Scholar] [CrossRef]
- Patterson, J.; Gibson, A. Deep Learning: A Practitioner’s Approach, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2017; pp. 125–140. [Google Scholar]
- Buddhahai, B.; Wongseree, W.; Rakkwamsuk, P. A non-intrusive load monitoring system using multi-label classification approach. Sustain. Cities Soc. 2018, 39, 621–630. [Google Scholar] [CrossRef]
- Cui, G.; Liu, B.; Luan, W. Neural Network with Extended Input for Estimating Electricity Consumption Using Background-based Data Generation. Energy Procedia 2019, 158, 2683–2688. [Google Scholar] [CrossRef]
- Seevers, J.-P.; Johst, J.; Weiß, T.; Meschede, H.; Hesselbach, J. Automatic Time Series Segmentation as the Basis for Unsupervised, Non-Intrusive Load Monitoring of Machine Tools. Procedia CIRP 2019, 81, 695–700. [Google Scholar] [CrossRef]
- Zoha, A.; Gluhak, A.; Imran, M.A.; Rajasegarar, S. Non-Intrusive Load Monitoring Approaches for Disaggregated Energy Sensing: A Survey. Sensors 2012, 12, 16838–16866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Wang, X.; Zhao, L.; Liu, Y. Admittance-based load signature construction for non-intrusive appliance load monitoring. Energy Build. 2018, 171, 209–219. [Google Scholar] [CrossRef]
- Hamid, O.; Barbarosou, M.; Papageorgas, P.; Prekas, K.; Salame, C.-T. Automatic recognition of electric loads analyzing the characteristic parameters of the consumed electric power through a Non-Intrusive Monitoring methodology. Energy Procedia 2017, 119, 742–751. [Google Scholar] [CrossRef]
- Welikala, S.; Thelasingha, N.; Akram, M.; Ekanayake, M.P.B.; Godaliyadda, G.M.R.I.; Ekanayake, J.B. Implementation of a robust real-time non-intrusive load monitoring solution. Appl. Energy 2019, 238, 1519–1529. [Google Scholar] [CrossRef]
- Kolter, J.; Jaakkola, T. Approximate inference in additive factorial HMMs with application to energy disaggregation. J. Mach. Learn. Res. 2012, 22, 1472–1482. [Google Scholar]
- Xia, M.; Liu, W.; Wang, K.; Zhang, X.; Xu, Y. Non-intrusive load disaggregation based on deep dilated residual network. Electr. Power Syst. Res. 2019, 170, 277–285. [Google Scholar] [CrossRef]
- Parson, O.; Ghosh, S.; Weal, M.; Rogers, A. An unsupervised training method for non-intrusive appliance load monitoring. Artif. Intell. 2014, 217, 1–19. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W. Neural NILM. In Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments, Seoul, South Korea, 4–5 November 2015; pp. 55–64. [Google Scholar]
- Zhang, C.; Zhong, M.; Wang, Z.; Goddard, N.; Sutton, C. Sequence-to-point learning with neural networks for non-intrusive load monitoring. arXiv 2017, arXiv:1612.09106. [Google Scholar]
- Kim, J.-G.; Lee, B. Appliance Classification by Power Signal Analysis Based on Multi-Feature Combination Multi-Layer LSTM. Energies 2019, 12, 2804. [Google Scholar] [CrossRef] [Green Version]
- Le, T.-T.-H.; Kim, H. Non-Intrusive Load Monitoring Based on Novel Transient Signal in Household Appliances with Low Sampling Rate. Energies 2018, 11, 3409. [Google Scholar] [CrossRef] [Green Version]
- Deep Learning-based Integrated Stacked Model for the Stock Market Prediction. Int. J. Eng. Adv. Technol. 2019, 9, 5167–5174. [CrossRef]
- Almonacid-Olleros, G.; Almonacid, G.; Fernández-Carrasco, J.I.; Quero, J.M. Opera.DL: Deep Learning Modelling for Photovoltaic System Monitoring. Proceedings 2019, 31, 50. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Dinesh, C.; Welikala, S.; Liyanage, Y.; Ekanayake, M.P.B.; Godaliyadda, R.I.; Ekanayake, J. Non-intrusive load monitoring under residential solar power influx. Appl. Energy 2017, 205, 1068–1080. [Google Scholar] [CrossRef]










| Artificial Neural Network (ANN) | External Classifier | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Inputs 1 | Output | Output | |||||||
| (i) | (ii) | (iii) | (iv) | (v) | (vi) | (vii) | (viii) | Real Power [W] | Active/Inactive 2 |
| 96.00 | 108.00 | 160.49 | 166.80 | 64.49 | 58.80 | 24 | 0 | 33.35 | Active |
| 87.33 | 79.82 | 164.70 | 158.81 | 77.37 | 78.99 | 85 | 0 | 1.18 | Inactive |
| Receiver Name | Houses | Threshold [W] |
|---|---|---|
| Fridge | 1, 2, 4, 5, 6 | 10 |
| Washing machine | 1 | 10 |
| Personal computer | 1 | 14 |
| Freezer | 1, 2, 3, 4 | 10/180 1 |
| Appliance Activity | |||
|---|---|---|---|
| Estimated | Active | Inactive | |
| Real | |||
| Active | TP | FN | |
| Inactive | FP | TN | |
| Parameter Name | Description | |
|---|---|---|
| Three-Dense-Layer DNN (3dl-DNN) | Convolutional Neural Network (CNN) | |
| Batch size | 16 1 | 16 |
| Loss function | Mean squared error | Mean squared error |
| Optimiser | Adam | Adam |
| Beta 1 | 0.9 | 0.9 |
| Epsilon (fuzz factor) | 1 × 10−8 | 1 × 10−8 |
| Beta 2 | 0.999 | 0.999 |
| Learning rate decay | 0 | 0 |
| Learning rate | 0.001 | 0.001 2 |
| Layer/Unit Name | Parameter Name | Value | ||||||
|---|---|---|---|---|---|---|---|---|
| the best multilayer perceptron (MLP) | ||||||||
| Hidden layer (dense) | No. of neurons | 11 | ||||||
| Activation function | Tanh | |||||||
| Output layer | No. of neurons | 1 | ||||||
| Activation function | Sigmoid | |||||||
| the best three-dense-layer deep neural network (3dl-DNN) | ||||||||
| the freezer in h1 1 | the fridge in h6, the freezer in h4 | others | ||||||
| 1st Dense | No. of neurons | 90 | 70 | 70 | ||||
| Activation function | ReLU | SoftPlus | ReLU | |||||
| 1st Dropout unit | Dropout value | 0.3 | 0.3 | 0.3 | ||||
| 2nd Dense | No. of neurons | 30 | 30 | 30 | ||||
| Activation function | ReLU | SoftPlus | ReLU | |||||
| 2nd Dropout unit | Dropout value | 0.3 | 0.3 | 0.3 | ||||
| 3rd Dense | No. of neurons | 1 | 1 | 1 | ||||
| Activation function | ReLU | SoftPlus | ReLU | |||||
| the best convolutional neural network (CNN) | ||||||||
| the fridge in h4 | the freezer in | the fridge in h6, the freezer in h4 | others | |||||
| h1 | h3 | |||||||
| 1D Convolution | Activation function | ReLU | ReLU | ReLU | ReLU | ReLU | ||
| Number of filters | 8 | 8 | 8 | 10 | 8 | |||
| Filter length | 3 | 3 | 3 | 3 | 3 | |||
| Max pooling | Pool length | 2 | 2 | 2 | 2 | 2 | ||
| 1st Dense | No. of neurons | 80 | 64 | 60 | 64 | 64 | ||
| Activation function | SoftPlus | SoftPlus | SoftPlus | ReLU | ReLU | |||
| 2nd Dense | No. of neurons | 1 | 1 | 1 | 1 | 1 | ||
| Activation function | SoftPlus | SoftPlus | SoftPlus | ReLU | ReLU | |||
| House No. (No. of Test Samples) | ANN Type | Accuracy (No. of Epochs) 1 | |||
|---|---|---|---|---|---|
| Fridge | Washing Machine | Personal Computer | Freezer | ||
| 1 (1585) | MLP 3dl-DNN CNN | 91.17 (151) 93.19 (200) 93.50 (350) | 90.41 (88) 71.42 (76) 97.60 (350) | 64.67 (146) 64.29 (200) 82.65 (350) | 84.92 (377) 66.50 (200) 84.23 (350) |
| 2 (1645) | MLP 3dl-DNN CNN | 95.62 (153) 95.99 (200) 95.74 (350) | – | – | 92.16 (321) 94.95 (200) 94.04 (350) |
| 3 (1422) | MLP 3dl-DNN CNN | – | – | – | 83.26 (224) 76.65 (200) 85.09 (153) |
| 4 (1946) | MLP 3dl-DNN CNN | 57.04 (235) 80.47 (200) 58.12 (350) | – | – | 77.34 (244) 72.46 (200) 75.23 (350) |
| 5 (2143) | MLP 3dl-DNN CNN | 88.80 (140) 89.87 (200) 91.60 (350) | – | – | – |
| 6 (1827) | MLP 3dl-DNN CNN | 87.30 (344) 88.29 (200) 89.27 (350) | – | – | – |
| Weighted average2 | MLP 3dl-DNN CNN | 83.38 89.23 85.08 | 90.41 71.42 97.60 | 64.67 64.29 82.65 | 84.13 77.54 84.21 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiński, T. Modelling the Disaggregated Demand for Electricity in Residential Buildings Using Artificial Neural Networks (Deep Learning Approach). Energies 2020, 13, 1263. https://doi.org/10.3390/en13051263
Jasiński T. Modelling the Disaggregated Demand for Electricity in Residential Buildings Using Artificial Neural Networks (Deep Learning Approach). Energies. 2020; 13(5):1263. https://doi.org/10.3390/en13051263
Chicago/Turabian StyleJasiński, Tomasz. 2020. "Modelling the Disaggregated Demand for Electricity in Residential Buildings Using Artificial Neural Networks (Deep Learning Approach)" Energies 13, no. 5: 1263. https://doi.org/10.3390/en13051263
APA StyleJasiński, T. (2020). Modelling the Disaggregated Demand for Electricity in Residential Buildings Using Artificial Neural Networks (Deep Learning Approach). Energies, 13(5), 1263. https://doi.org/10.3390/en13051263