Daily Crude Oil Price Forecasting Based on Improved CEEMDAN, SCA, and RVFL: A Case Study in WTI Oil Market
Abstract
:1. Introduction
- (1)
- We develop a self-optimizing ensemble learning paradigm incorporating ICEEMDAN, SCA, and RVFL for crude oil price forecasting. To our knowledge, this is the first time that the ensemble framework is introduced into the field of crude oil price forecasting.
- (2)
- To further enhance forecasting performance, SCA is employed to optimize the parameter settings for ICEEMDAN and RVFL.
- (3)
- The experiments show that our proposed ICEEMDAN-SCA-RVFL is significantly superior to the single and ensemble benchmark models for crude oil price forecasting.
2. Preliminaries
2.1. Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN)
2.2. Sine Cosine Algorithm (SCA)
2.3. Random Vector Functional Link (RVFL) Neural Network
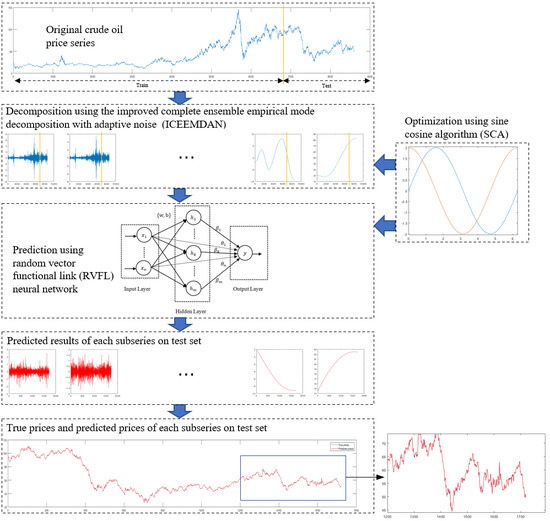
3. ICEEMDAN-SCA-RVFL: The Proposed Approach for Crude Oil Price Forecasting
4. A Case Study in WTI Oil Market
4.1. Data Description
4.2. Evaluation Indices
4.3. Experimental Settings
4.4. Results and Analysis
4.4.1. Single Models
4.4.2. Ensemble Models
4.4.3. Comparison with Extant Ensemble Models
5. Discussion
5.1. The Evolution Efficiency of SCA
5.2. The Prediction Result of Each Individual Component
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.; Li, J.; Yu, L. A deep learning ensemble approach for crude oil price forecasting. Energy Econ. 2017, 66, 9–16. [Google Scholar] [CrossRef]
- Zhu, B.; Shi, X.; Chevallier, J.; Wang, P.; Wei, Y.M. An adaptive multiscale ensemble learning paradigm for nonstationary and nonlinear energy price time series forecasting. J. Forecast. 2016, 35, 633–651. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Y.; Zhou, T.; Li, T. An adaptive hybrid learning paradigm integrating CEEMD, ARIMA and SBL for crude oil price forecasting. Energies 2019, 12, 1239. [Google Scholar] [CrossRef] [Green Version]
- Lanza, A.; Manera, M.; Giovannini, M. Modeling and forecasting cointegrated relationships among heavy oil and product prices. Energy Econ. 2005, 27, 831–848. [Google Scholar] [CrossRef]
- e Silva, E.G.d.S.; Legey, L.F.; e Silva, E.A.d.S. Forecasting oil price trends using wavelets and hidden Markov models. Energy Econ. 2010, 32, 1507–1519. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhuang, X.H. Application of ARIMA model in short-term prediction of international crude oil price. Adv. Mater. Res. Trans. Tech. Publ. 2013, 798, 979–982. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Y.; Huang, D. Forecasting crude oil market volatility: Further evidence using GARCH-class models. Energy Econ. 2010, 32, 1477–1484. [Google Scholar] [CrossRef]
- Ramyar, S.; Kianfar, F. Forecasting crude oil prices: A comparison between artificial neural networks and vector autoregressive models. Comput. Econ. 2019, 53, 743–761. [Google Scholar] [CrossRef]
- Mirmirani, S.; Li, H.C. A comparison of VAR and neural networks with genetic algorithm in forecasting price of oil. Adv. Econometr. 2004, 19, 203–223. [Google Scholar]
- Bashiri Behmiri, N.; Pires Manso, J.R. Crude oil Price Forecasting Techniques: A Comprehensive Review of Literature. Altern. Invest. Anal. Rev. 2013, 2, 30–49. [Google Scholar] [CrossRef]
- Mostafa, M.M.; El-Masry, A.A. Oil price forecasting using gene expression programming and artificial neural networks. Econ. Model. 2016, 54, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Kulkarni, S.; Haidar, I. Forecasting model for crude oil price using artificial neural networks and commodity futures prices. arXiv 2009, arXiv:0906.4838. [Google Scholar]
- Xie, W.; Yu, L.; Xu, S.; Wang, S. A new method for crude oil price forecasting based on support vector machines. In Proceeding of the International Conference on Computational Science, Reading, UK, 28–31 May 2006; pp. 444–451. [Google Scholar]
- Shu-rong, L.; Yu-lei, G. Crude oil price prediction based on a dynamic correcting support vector regression machine. Abstr. Appl. Anal. 2013, 2013, 528678. [Google Scholar] [CrossRef]
- Li, T.; Hu, Z.; Jia, Y.; Wu, J.; Zhou, Y. Forecasting crude oil prices using ensemble empirical mode decomposition and sparse Bayesian learning. Energies 2018, 11, 1882. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Athanasopoulos, G.; Hyndman, R.J.; Wang, S. Crude oil price forecasting based on internet concern using an extreme learning machine. Int. J. Forecast. 2018, 34, 665–677. [Google Scholar] [CrossRef]
- Gumus, M.; Kiran, M.S. Crude oil price forecasting using XGBoost. In Proceedings of the 2017 International Conference on Computer Science and Engineering (UBMK), Antalya, Turkey, 5–7 October 2017; pp. 1100–1103. [Google Scholar]
- Tang, L.; Wu, Y.; Yu, L. A non-iterative decomposition-ensemble learning paradigm using RVFL network for crude oil price forecasting. Appl. Soft Comput. 2018, 70, 1097–1108. [Google Scholar] [CrossRef]
- Mingming, T.; Jinliang, Z. A multiple adaptive wavelet recurrent neural network model to analyze crude oil prices. J. Econ. Bus. 2012, 64, 275–286. [Google Scholar] [CrossRef]
- Yu, L.; Dai, W.; Tang, L.; Wu, J. A hybrid grid-GA-based LSSVR learning paradigm for crude oil price forecasting. Neural Comput. Appl. 2016, 27, 2193–2215. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; He, K.; Zheng, A. Multi-step-ahead crude oil price forecasting using a hybrid grey wave model. Phys. A Stat. Mech. Appl. 2018, 501, 98–110. [Google Scholar] [CrossRef]
- Wang, S.; Yu, L.; Lai, K.K. A novel hybrid AI system framework for crude oil price forecasting. In Proceedings of the Chinese Academy of Sciences Symposium on Data Mining and Knowledge Management, Beijing, China, 12–14 July 2004; pp. 233–242. [Google Scholar]
- Tehrani, R.; Khodayar, F. A hybrid optimized artificial intelligent model to forecast crude oil using genetic algorithm. Afr. J. Bus. Manag. 2011, 5, 13130. [Google Scholar] [CrossRef]
- Li, T.; Zhou, Y.; Li, X.; Wu, J.; He, T. Forecasting daily crude oil prices using improved CEEMDAN and ridge regression-based predictors. Energies 2019, 12, 3603. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Li, T.; Shi, J.; Qian, Z. A CEEMDAN and XGBOOST-based approach to forecast crude oil prices. Complexity 2019, 2019, 4392785. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Qian, Z.; He, T. Short-term Load Forecasting with Improved CEEMDAN and GWO-based Multiple Kernel ELM. Complexity 2020, 2020, 1209547. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, T.; Li, T. Detecting Epileptic Seizures in EEG Signals with Complementary Ensemble Empirical Mode Decomposition and Extreme Gradient Boosting. Entropy 2020, 22, 140. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.; Zhang, X.; Yu, L.; Lai, K.K.; Wang, S. An integrated model using wavelet decomposition and least squares support vector machines for monthly crude oil prices forecasting. New Math. Natural Comput. 2011, 7, 299–311. [Google Scholar] [CrossRef]
- He, K.; Zha, R.; Wu, J.; Lai, K.K. Multivariate EMD-based modeling and forecasting of crude oil price. Sustainability 2016, 8, 387. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Zhou, M.; Guo, C.; Luo, M.; Wu, J.; Pan, F.; Tao, Q.; He, T. Forecasting crude oil price using EEMD and RVM with adaptive PSO-based kernels. Energies 2016, 9, 1014. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wu, H.; Li, Y. Smart wind speed forecasting using EWT decomposition, GWO evolutionary optimization, RELM learning and IEWT reconstruction. Energy Convers. Manag. 2018, 161, 266–283. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C.; Wu, C. Modelling of carbon price in two real carbon trading markets. J. Clean. Prod. 2020, 244, 118556. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Niu, T.; Du, P. A hybrid forecasting system based on a dual decomposition strategy and multi-objective optimization for electricity price forecasting. Appl. Energy 2019, 235, 1205–1225. [Google Scholar] [CrossRef]
- Khorramdel, B.; Azizi, M.; Safari, N.; Chung, C.; Mazhari, S. A Hybrid Probabilistic Wind Power Prediction Based on An Improved Decomposition Technique and Kernel Density Estimation. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Deng, W.; Liu, H.; Xu, J.; Zhao, H.; Song, Y. An improved quantum-inspired differential evolution algorithm for deep belief network. IEEE Trans. Instrum. Meas. 2020. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Yang, X.; Xiong, J.; Sun, M.; Li, B. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Appl. Soft Comput. 2017, 59, 288–302. [Google Scholar] [CrossRef]
- Hekimoğlu, B. Sine-cosine algorithm-based optimization for automatic voltage regulator system. Trans. Inst. Meas. Control 2019, 41, 1761–1771. [Google Scholar] [CrossRef]
- Majhi, S.K. An efficient feed foreword network model with sine cosine algorithm for breast cancer classification. Int. J. Syst. Dyn. Appl. 2018, 7, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Pao, Y.H.; Takefuji, Y. Functional-link net computing: Theory, system architecture, and functionalities. Computer 1992, 25, 76–79. [Google Scholar] [CrossRef]
- Igelnik, B.; Pao, Y.H. Stochastic choice of basis functions in adaptive function approximation and the functional-link net. IEEE Trans. Neural Netw. 1995, 6, 1320–1329. [Google Scholar] [CrossRef] [Green Version]
- Aggarwal, A.; Tripathi, M. Short-term solar power forecasting using random vector functional link (RVFL) network. In Ambient Communications and Computer Systems; Springer: Singapore, 2018; pp. 29–39. [Google Scholar]
- Li, T.; Shi, J.; Li, X.; Wu, J.; Pan, F. Image encryption based on pixel-level diffusion with dynamic filtering and DNA-level permutation with 3D Latin cubes. Entropy 2019, 21, 319. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Shi, J.; Li, T. A novel image encryption approach based on a hyperchaotic system, pixel-level filtering with variable kernels, and DNA-level diffusion. Entropy 2020, 22, 5. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Yang, M.; Wu, J.; Jing, X. A novel image encryption algorithm based on a fractional-order hyperchaotic system and DNA computing. Complexity 2017, 2017, 9010251. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Xie, Z.; Wu, J.; Li, T. Image encryption based on dynamic filtering and bit cuboid operations. Complexity 2019, 2019, 7485621. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Xu, J.; Deng, W. Performance prediction using high-order differential mathematical morphology gradient spectrum entropy and extreme learning machine. IEEE Trans. Instrum. Meas. 2019. [Google Scholar] [CrossRef]
- Qiu, X.; Suganthan, P.N.; Amaratunga, G.A. Electricity load demand time series forecasting with empirical mode decomposition based random vector functional link network. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 001394–001399. [Google Scholar]
- Ren, Y.; Suganthan, P.N.; Srikanth, N.; Amaratunga, G. Random vector functional link network for short-term electricity load demand forecasting. Inf. Sci. 2016, 367, 1078–1093. [Google Scholar] [CrossRef]
- EIA Website. Available online: https://www.eia.gov/dnav/pet/hist/rwtcD.htm (accessed on 14 February 2020).





| Method | Description | Parameters |
|---|---|---|
| EEMD | Ensemble empirical mode decomposition | Noise standard deviation: 0.2 |
| Number of realizations: 100 | ||
| ICEEMDAN | Improved complete EEMD with adaptive noise | Noise standard deviation: 0.2 |
| Number of realizations: 100 | ||
| ARIMA | Autoregressive integrated moving average | Akaike information criterion (AIC) to determine parameters (p-d-q) |
| BPNN | Back propagation neural network | Size of the hidden layer: 10 |
| Maximum training epochs: 1000 | ||
| Learning rate: 0.001 | ||
| LSSVR | Least square support vector regression with a RBF kernel | Regularization parameter: |
| Width of the RBF kernel: | ||
| RVFL | Random vector functional link | Number of hidden neurons: 10 |
| Activation Function: Sigmoid | ||
| Random type: Gaussian | ||
| SCA | Sine cosine algorithm | Population size: 50 |
| Maximum generation: 150 | ||
| Fitness function: RMSE | ||
| ICEEMDAN-SCA-RVFL | The proposed ensemble model | Noise standard deviation in ICEEMDAN: [0.01, 0.4] |
| Number of realizations in ICEEMDAN: [50, 500] | ||
| Number of hidden neurons in RVFL: [5, 50] | ||
| Activation Function in RVFL: {1: sigmoid, 2: sine, 3: hardlim, 4: tribas, 5: radbas, 6: sign} | ||
| Mode in RVFL: {1: regularized least square, 2: Moore-Penrose pseudoinverse} | ||
| Lag in RVFL: [3, 20] | ||
| Bias in RVFL: {1: true, 2: false} | ||
| Random type in RVFL: {1: Gaussian, 2: uniform} | ||
| Scale in RVFL: [0.1, 1] | ||
| Scale mode in RVFL: {1: scale the features for all neurons 2: scale the features for each hidden neuron, 3: scale the range of the randomization for uniform distribution} |
| Horizon | Criterion | SCA-RVFL | RVFL | LSSVR | BPNN | ARIMA |
|---|---|---|---|---|---|---|
| MAPE | 0.0157 | 0.0157 | 0.0158 | 0.0158 | 0.0160 | |
| 1 | RMSE | 1.2183 | 1.2205 | 1.2234 | 1.2307 | 1.2365 |
| Dstat | 0.7522 | 0.7516 | 0.5073 | 0.5032 | 0.4959 | |
| MAPE | 0.0272 | 0.0273 | 0.0274 | 0.0275 | 0.0280 | |
| 3 | RMSE | 2.0331 | 2.0498 | 2.0505 | 2.0613 | 2.1022 |
| Dstat | 0.6486 | 0.6562 | 0.5061 | 0.5073 | 0.5029 | |
| MAPE | 0.0384 | 0.0384 | 0.0392 | 0.0398 | 0.0412 | |
| 6 | RMSE | 2.8463 | 2.8834 | 2.8854 | 2.9320 | 3.0276 |
| Dstat | 0.6248 | 0.6178 | 0.4933 | 0.4986 | 0.4956 |
| Horizon | Tested Model | Benchmark Model | |||
|---|---|---|---|---|---|
| RVFL | LSSVR | BPNN | ARIMA | ||
| SCA-RVFL | −0.6246(0.5323) | −1.2119(0.2257) | −2.3647(0.0018) | −2.7381(0.0062) | |
| RVFL | −0.9619(0.3362) | −1.4704(0.1416) | −2.1955(0.0283) | ||
| 1 | LSSVR | −1.0765(0.2819) | −1.8863(0.0594) | ||
| BPNN | −0.8578(0.3912) | ||||
| SCA-RVFL | −3.2376(0.0012) | −3.8828(0.0001) | −4.9342(0.0000) | −4.1835(0.0000) | |
| RVFL | −0.17891(0.8580) | −4.1226(0.0000) | −2.8057(0.0051) | ||
| 3 | LSSVR | −4.1267(0.0000) | −2.7791(0.0055) | ||
| BPNN | 0.3392(0.7345) | ||||
| SCA-RVFL | −4.4805(0.0000) | −5.2037(0.0000) | −5.5660(0.0000) | −5.5436(0.0000) | |
| RVFL | −0.3742(0.7083) | −3.9099(0.0000) | −3.7978(0.0002) | ||
| 6 | LSSVR | −3.7347(0.0002) | −3.8514(0.0001) | ||
| BPNN | −2.3321(0.0198) | ||||
| Decomposition | Horizon | Criterion | SCA-RVFL | RVFL | LSSVR | BPNN | ARIMA |
|---|---|---|---|---|---|---|---|
| 1 | MAPE | 0.0086 | 0.0087 | 0.0097 | 0.0101 | 0.0163 | |
| RMSE | 0.6340 | 0.6624 | 0.7027 | 0.7430 | 1.1439 | ||
| Dstat | 0.8045 | 0.8092 | 0.7912 | 0.7941 | 0.7027 | ||
| EEMD | 3 | MAPE | 0.0099 | 0.0100 | 0.0106 | 0.0112 | 0.0337 |
| RMSE | 0.7445 | 0.7538 | 0.7876 | 0.8252 | 2.3392 | ||
| Dstat | 0.7755 | 0.7720 | 0.7650 | 0.7342 | 0.5794 | ||
| 6 | MAPE | 0.0126 | 0.0128 | 0.0133 | 0.0138 | 0.1328 | |
| RMSE | 0.9351 | 0.9614 | 0.9879 | 1.0236 | 8.2344 | ||
| Dstat | 0.7080 | 0.7027 | 0.6992 | 0.7010 | 0.5207 | ||
| 1 | MAPE | 0.0035 | 0.0040 | 0.0047 | 0.0045 | 0.0121 | |
| RMSE | 0.2801 | 0.3187 | 0.3559 | 0.3601 | 0.8205 | ||
| Dstat | 0.9273 | 0.9186 | 0.9093 | 0.8988 | 0.7720 | ||
| ICEEMDAN | 3 | MAPE | 0.0074 | 0.0076 | 0.0078 | 0.0078 | 0.0348 |
| RMSE | 0.5655 | 0.5874 | 0.6007 | 0.5943 | 2.3152 | ||
| Dstat | 0.8418 | 0.8389 | 0.8301 | 0.8325 | 0.6021 | ||
| 6 | MAPE | 0.0105 | 0.0107 | 0.0113 | 0.0117 | 0.1322 | |
| RMSE | 0.7981 | 0.8165 | 0.8596 | 0.858 | 7.8432 | ||
| Dstat | 0.7615 | 0.7487 | 0.7452 | 0.7406 | 0.5183 |
| Horizon | Decomposition | Tested Model | ICEEMDAN | EEMD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RVFL | LSSVR | BPNN | ARIMA | SCA-RVFL | RVFL | LSSVR | BPNN | ARIMA | ||||
| 1 | ICEEMDAN | SCA-RVFL | −5.5700(0.0000) | −9.4457(0.0000) | −6.2371(0.0000) | −27.9480(0.0000) | −21.4060(0.0000) | −21.4970(0.0000) | −22.6060(0.0000) | −22.2160(0.0000) | −30.1000(0.0000) | |
| RVFL | −3.3976(0.0007) | −3.0759(0.0021) | −26.1540(0.0000) | −18.5100(0.0000) | −18.6720(0.0000) | −20.2940(0.0000) | −20.3720(0.0000) | −29.2790(0.0000) | ||||
| LSSVR | −0.3439(0.7309) | −25.8850(0.0000) | −18.6780(0.0000) | −18.8750(0.0000) | −20.7850(0.0000) | −20.6620(0.0000) | −29.0770(0.0000) | |||||
| BPNN | −24.1350(0.0000) | −16.6170(0.0000) | −16.8710(0.0000) | −19.0640(0.0000) | −19.4070(0.0000) | −28.4780(0.0000) | ||||||
| ARIMA | 10.4890(0.0000) | 10.0040(0.0000) | 6.5318(0.0000) | 3.8888(0.0001) | −19.2830(0.0000) | |||||||
| EEMD | SCA-RVFL | −4.6072(0.0000) | −10.0130(0.0000) | −10.6500(0.0000) | −20.9060(0.0000) | |||||||
| RVFL | −8.9065(0.0000) | −9.8407(0.0000) | −20.5820(0.0000) | |||||||||
| LSSVR | −5.8255(0.0000) | −18.5970(0.0000) | ||||||||||
| BPNN | −16.0660(0.0000) | |||||||||||
| 3 | ICEEMDAN | SCA-RVFL | −2.8872(0.0039) | −4.4986(0.0000) | −3.9116(0.0000) | −27.0070(0.0000) | −13.6560(0.0000) | −13.9180(0.0000) | −15.5620(0.0000) | −17.3230(0.0000) | −33.1140(0.0000) | |
| RVFL | −1.9809(0.0478) | −0.9605(0.3369) | −26.8910(0.0000) | −12.7810(0.0000) | −13.3050(0.0000) | −14.6030(0.0000) | −16.9960(0.0000) | −32.9940(0.0000) | ||||
| LSSVR | 0.8108(0.4176) | −26.9710(0.0000) | −12.0680(0.0000) | −12.5820(0.0000) | −14.3300(0.0000) | −15.7790(0.0000) | −33.0980(0.0000) | |||||
| BPNN | −26.8710(0.0000) | −12.8150(0.0000) | −13.3570(0.0000) | −14.2760(0.0000) | −16.2940(0.0000) | −32.9630(0.0000) | ||||||
| ARIMA | 25.7040(0.0000) | 25.6680(0.0000) | 25.6240(0.0000) | 24.8070(0.0000) | −1.1371(0.2557) | |||||||
| EEMD | SCA-RVFL | −2.6908(0.0072) | −3.0556(0.0023) | −9.6047(0.0000) | −31.5370(0.0000) | |||||||
| RVFL | −2.4007(0.0165) | −8.5477(0.0000) | −31.5140(0.0000) | |||||||||
| LSSVR | −2.4394(0.0148) | −31.5540(0.0000) | ||||||||||
| BPNN | −30.4040(0.0000) | |||||||||||
| 6 | ICEEMDAN | SCA-RVFL | −2.8224(0.0048) | −6.2393(0.0000) | −6.8481(0.0000) | −44.3450(0.0000) | −10.2880(0.0000) | −11.5500(0.0000) | −12.4570(0.0000) | −13.2560(0.0000) | −47.3470(0.0000) | |
| RVFL | −4.4022(0.0000) | −5.3816(0.0000) | −44.3100(0.0000) | −8.9581(0.0000) | −10.7610(0.0000) | −11.4000(0.0000) | −12.4550(0.0000) | −47.3210(0.0000) | ||||
| LSSVR | 0.1737(0.8621) | −44.2780(0.0000) | −5.3218(0.0000) | −6.8608(0.0000) | −9.5910(0.0000) | −9.3727(0.0000) | −47.2820(0.0000) | |||||
| BPNN | −44.3260(0.0000) | −5.8458(0.0000) | −7.5255(0.0000) | −9.2845(0.0000) | −10.6020(0.0000) | −47.2740(0.0000) | ||||||
| ARIMA | 44.1850(0.0000) | 44.1270(0.0000) | 44.1660(0.0000) | 44.0680(0.0000) | −4.2675(0.0000) | |||||||
| EEMD | SCA-RVFL | −4.4304(0.0000) | −6.4338(0.0000) | −8.5997(0.0000) | −47.1810(0.0000) | |||||||
| RVFL | −2.9815(0.0029) | −5.8995(0.0000) | −47.1380(0.0000) | |||||||||
| LSSVR | −3.7208(0.0002) | −47.1570(0.0000) | ||||||||||
| BPNN | −47.0580(0.0000) | |||||||||||
| Horizon | Criterion | ICEEMDAN-SCA-RVFL | ICEEMDAN-DE-RR | CEEMD-A&S-SBL | EEMD-APSO-RVM |
|---|---|---|---|---|---|
| 1 | MAPE | 0.0035 | 0.0037 | 0.0046 | 0.0090 |
| RMSE | 0.2801 | 0.2915 | 0.3524 | 0.6668 | |
| Dstat | 0.9273 | 0.9226 | 0.9093 | 0.8016 | |
| 3 | MAPE | 0.0074 | 0.0077 | 0.0082 | 0.0110 |
| RMSE | 0.5655 | 0.5888 | 0.6285 | 0.8273 | |
| Dstat | 0.8418 | 0.8371 | 0.8173 | 0.7487 | |
| 6 | MAPE | 0.0105 | 0.0117 | 0.0119 | 0.0139 |
| RMSE | 0.7981 | 0.8835 | 0.8962 | 1.0277 | |
| Dstat | 0.7615 | 0.7208 | 0.7283 | 0.6928 |
| Horizon | Tested Model | Benchmark Model | ||
|---|---|---|---|---|
| ICEEMDAN-DE-RR | CEEMD-A&S-SBL | EEMD-APSO-RVM | ||
| 1 | ICEEMDAN-SCA-RVFL | −4.5250(0.0000) | −12.7310(0.0000) | −20.1070(0.0000) |
| ICEEMDAN-DE-RR | −11.3950(0.0000) | −20.0280(0.0000) | ||
| CEEMD-A&S-SBL | −18.1600(0.0000) | |||
| 3 | ICEEMDAN-SCA-RVFL | −3.9699(0.0000) | −7.5493(0.0000) | −15.7140(0.0000) |
| ICEEMDAN-DE-RR | −6.0151(0.0000) | −16.4830(0.0000) | ||
| CEEMD-A&S-SBL | −14.5060(0.0000) | |||
| 6 | ICEEMDAN-SCA-RVFL | −9.1429(0.0000) | −7.9592(0.0000) | −13.2130(0.0000) |
| ICEEMDAN-DE-RR | −1.3989(0.1620) | −9.7131(0.0000) | ||
| CEEMD-A&S-SBL | −8.1452(0.0000) | |||
| Tested Model | Component | RMSE | MAPE | Dstat |
|---|---|---|---|---|
| IMF1 | 0.2885 | 3.6136 | 0.8493 | |
| IMF2 | 0.1119 | 1.1606 | 0.9221 | |
| IMF3 | 0.0136 | 0.4906 | 0.9820 | |
| IMF4 | 0.0019 | 0.0075 | 0.9971 | |
| IMF5 | 0.0003 | 0.0017 | 1.0000 | |
| ICEEMDAN-SCA-RVFL | IMF6 | 1.0000 | ||
| IMF7 | 1.0000 | |||
| IMF8 | 1.0000 | |||
| IMF9 | 1.0000 | |||
| IMF10 | 1.0000 | |||
| IMF11 | 1.0000 | |||
| Residue | 0.9994 | |||
| Raw oil price series | 0.2801 | 0.0035 | 0.9273 | |
| IMF1 | 0.3192 | 4.4029 | 0.8307 | |
| IMF2 | 0.1141 | 1.8793 | 0.9157 | |
| IMF3 | 0.0147 | 0.4197 | 0.9848 | |
| IMF4 | 0.0021 | 0.01579 | 0.9948 | |
| IMF5 | 0.0003 | 0.0010 | 1.0000 | |
| ICEEMDAN-RVFL | IMF6 | 1.0000 | ||
| IMF7 | 1.0000 | |||
| IMF8 | 1.0000 | |||
| IMF9 | 1.0000 | |||
| IMF10 | 1.0000 | |||
| IMF11 | 1.0000 | |||
| Residue | 0.0001 | 0.9779 | ||
| Raw oil price series | 0.3187 | 0.0040 | 0.9186 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Miu, F.; Li, T. Daily Crude Oil Price Forecasting Based on Improved CEEMDAN, SCA, and RVFL: A Case Study in WTI Oil Market. Energies 2020, 13, 1852. https://doi.org/10.3390/en13071852
Wu J, Miu F, Li T. Daily Crude Oil Price Forecasting Based on Improved CEEMDAN, SCA, and RVFL: A Case Study in WTI Oil Market. Energies. 2020; 13(7):1852. https://doi.org/10.3390/en13071852
Chicago/Turabian StyleWu, Jiang, Feng Miu, and Taiyong Li. 2020. "Daily Crude Oil Price Forecasting Based on Improved CEEMDAN, SCA, and RVFL: A Case Study in WTI Oil Market" Energies 13, no. 7: 1852. https://doi.org/10.3390/en13071852
APA StyleWu, J., Miu, F., & Li, T. (2020). Daily Crude Oil Price Forecasting Based on Improved CEEMDAN, SCA, and RVFL: A Case Study in WTI Oil Market. Energies, 13(7), 1852. https://doi.org/10.3390/en13071852