Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part I—Experimental Study and Charge Injection Hypothesis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Manufacturing
2.2. Roughness Enhanced Charge Injection
2.3. Space Charge Measurement
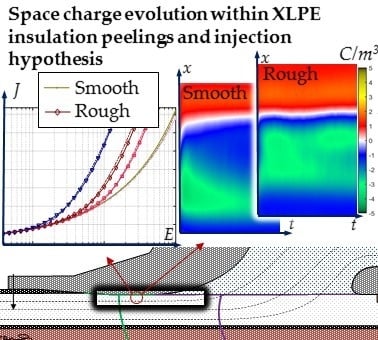
3. Results
3.1. Roughness Enhanced Charge Injection
3.2. Space Charge Measurement
3.2.1. Impact of Sample Orientation and Polarity
3.2.2. Impact of Poling Field Strength
3.2.3. Impact of Temperature
4. Discussion
4.1. Roughness Enhanced Charge Injection
4.2. Overall Observations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tanaka, T. Space charge injected via interfaces and tree initiation in polymers. IEEE Trans. Dielectr. Electr. Insul. 2001, 8, 733–743. [Google Scholar] [CrossRef]
- Morshuis, P. Interfaces: To be avoided or to be treasured? What do we think we know? In Proceedings of the IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Taleb, M.; Teyssedre, G.; Le Roy, S. Role of the interface on charge build-up in a low-density polyethylene: Surface roughness and nature of the electrode. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Virginia Beach, VA, USA, 18–21 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 112–115. [Google Scholar] [CrossRef]
- Novikov, S.V. Rough electrode surface: Effect on charge carrier injection and transport in organic devices. Macromol. Symp. 2004, 212, 191–200. [Google Scholar] [CrossRef]
- Doedens, E.H. Characterization of Different Interface Types for HVDC Extruded Cable Applications. Lic. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2018. Available online: https://research.chalmers.se/publication/502706/file/502706_Fulltext.pdf (accessed on 6 April 2020).
- Doedens, E.; Jarvid, M.; Serdyuk, Y.V.; Guffond, R.; Charrier, D. Local Surface Field- and Charge Distributions and Their Impact on Breakdown Voltage for HVDC Cable Insulation. In Proceedings of the International Conference on Insulated Power Cables (Jicable), Cigré, Versailles, France, 23–27 June 2019. [Google Scholar]
- Doedens, E.; Jarvid, E.M.; Frohne, C.; Gubanski, S.M. Enhanced charge injection in rough HVDC extruded cable interfaces. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1911–1918. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v.5.3. Available online: www.comsol.com (accessed on 16 April 2020).
- Doedens, E.; Jarvid, M.; Gubanski, S.; Frohne, C. Cable surface preparation: Chemical, physical and electrical characterization and impact on breakdown voltage. In Proceedings of the International Symposium on HVDC Cable Systems (Jicable-HVDC), Dunkirk, France, 20–22 November 2017. [Google Scholar]
- Good, R.H.; Müller, E.W. Field Emission. In Electron-Emission Gas Discharges I/Elektronen-Emission Gasentladungen, I. Encyclopedia of Physics/Handbuch der Physik; Springer: Berlin/Heidelberg, Germany, 1956; pp. 176–231. ISBN 978-3-642-45846-0. [Google Scholar]
- Guffond, R.; Combessis, A.; Hole, S. Contribution of polymer microstructure to space charge, dielectric properties and electrical conduction. In Proceedings of the 2016 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Toronto, ON, Canada, 16–19 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 141–144. [Google Scholar] [CrossRef]
- Baudoin, F.; Laurent, C.; Le Roy, S.; Teyssedre, G. Charge packets modeling in insulating polymers based on transport description. In Proceedings of the Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Montreal, QC, Canada, 14–17 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 665–668. [Google Scholar] [CrossRef]
- Moyassari, A.; Unge, M.; Hedenqvist, M.S.; Gedde, U.W.; Nilsson, F. First-principle simulations of electronic structure in semicrystalline polyethylene. J. Chem. Phys. 2017, 146, 204901. [Google Scholar] [CrossRef] [PubMed]
- Hoang, A.; Pallon, L.; Liu, D.; Serdyuk, Y.; Gubanski, S.; Gedde, U. Charge Transport in LDPE Nanocomposites Part I—Experimental Approach. Polymers 2016, 8, 87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoang, A.T.; Serdyuk, Y.V.; Gubanski, S.M. Charge Transport in LDPE Nanocomposites Part II—Computational Approach. Polymers 2002, 8, 103. [Google Scholar] [CrossRef] [PubMed]
- Serra, S.; Tosatti, E.; Iarlori, S.; Scandolo, S.; Santoro, G.; Albertini, M. Interchain states and the negative electron affinity of polyethylene. In Proceedings of the 1998 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (Cat. No.98CH36257), Atlanta, GA, USA, 25–28 October 1998; IEEE: Piscataway, NJ, USA, 1998; Volume 1, pp. 19–22. [Google Scholar] [CrossRef]
- Nilsson, S.; Hjertberg, T.; Smedberg, A. Structural effects on thermal properties and morphology in XLPE. Eur. Polym. J. 2010, 46, 1759–1769. [Google Scholar] [CrossRef]
- Boufayed, F.; Teyssèdre, G.; Laurent, C.; Le Roy, S.; Dissado, L.A.; Ségur, P.; Montanari, G.C. Models of bipolar charge transport in polyethylene. J. Appl. Phys. 2006, 100, 104–105. [Google Scholar] [CrossRef] [Green Version]











| Surface Type | A: Rough Abraded | B: Abraded | C: Smooth Abraded | D: Backside | E: Remolded |
|---|---|---|---|---|---|
| Roughness, Sa 1 | 74.6 | 34.6 | 19.0 | 12.5 | 1 |
| Roughness, Sdq 1 | 75.3 | 37.6 | 23.6 | 12.4 | 1 |
| Max field enhancement, FEFmax 2 | 9 | 6 | 4 | 1.8 | 1.1 |
| Injection field parameter, βs, βFN 3 | 13 (9) | 6.5 | 4.3 | 1.9 | 1.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doedens, E.; Jarvid, E.M.; Guffond, R.; Serdyuk, Y.V. Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part I—Experimental Study and Charge Injection Hypothesis. Energies 2020, 13, 2005. https://doi.org/10.3390/en13082005
Doedens E, Jarvid EM, Guffond R, Serdyuk YV. Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part I—Experimental Study and Charge Injection Hypothesis. Energies. 2020; 13(8):2005. https://doi.org/10.3390/en13082005
Chicago/Turabian StyleDoedens, Espen, E. Markus Jarvid, Raphaël Guffond, and Yuriy V. Serdyuk. 2020. "Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part I—Experimental Study and Charge Injection Hypothesis" Energies 13, no. 8: 2005. https://doi.org/10.3390/en13082005
APA StyleDoedens, E., Jarvid, E. M., Guffond, R., & Serdyuk, Y. V. (2020). Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part I—Experimental Study and Charge Injection Hypothesis. Energies, 13(8), 2005. https://doi.org/10.3390/en13082005