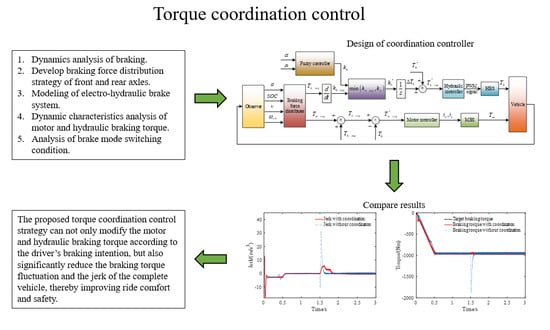
The dynamic coordination control strategy of brake mode switching developed in this paper is shown in the
Figure 8. Firstly, the target hydraulic braking torque,
, and the target motor braking torque,
, are preliminarily distributed based on the vehicle state parameters by the braking force distribution controller. Secondly, the target hydraulic braking torque is modified through fuzzy control rules based on the pedal opening and its change rate, to reflect the driver’s braking intention. Then, the target motor braking torque is corrected by the actual hydraulic braking torque (
) output by the HBS, and the rapid response of the MBS is used to compensate for the hydraulic braking torque, to achieve a smooth transition of the braking mode. Finally, the HBS and the MBS are controlled by the hydraulic and motor braking controller, respectively, to respond to the modified target braking torque
and
, and then output the actual hydraulic braking torque,
, and actual motor braking torque,
, to decelerate the vehicle.
4.2.1. The Modification of Target Hydraulic Braking Torque
The target change rates of target hydraulic braking torque during braking are
where
represents the target change rates of hydraulic braking torque.
During the mode switching, the upper limit of the change rate of the hydraulic braking torque,
, is determined by the fuzzy controller, which is designed based on the brake pedal stroke,
, and its change rate,
. Then the upper limit of the change rate,
, is compared with the target change rate
, to determine the modified target change rate.
The increment of the modified target hydraulic braking torque,
, can be obtained by the integration of the modified target change rate. Therefore, the modified target braking torque of the HBS is
where
represents the target braking torque of the HBS modified by the coordination controller; and
is the initial braking torque at the moment when the mode is switched.
During mode switching, the driver’s braking intention is reflected by the brake pedal stroke and the brake pedal stroke change rate. Then the fuzzy controller outputs the upper limit of the change rate of the target hydraulic braking torque, so as to realize the modification of the target hydraulic braking torque. The fuzzy subsets of brake pedal stroke, brake pedal stroke change rate, and the upper limit of the change rate of the hydraulic braking torque are
; therefore, the input and output of the fuzzy controller can be described as
where VS, S, MS, M, ML, L, and VL represent very small, small medium, medium, medium large, large, and very large, respectively.
The fuzzy control rules are shown in
Table 8, and the membership function of input and output variables of fuzzy controller are shown in
Figure 9,
Figure 10 and
Figure 11. The fuzzy control rules are formulated based on the following experiences:
Criterion 1: If and are S, then is MS. In this case, the brake pedal stroke and its change rate are small; it can be considered that the driver pays more attention to the ride comfort during mode switching, and the upper limit of the change rate of the hydraulic braking torque takes a medium-small value.
Criterion 2: If is S and is L, then is ML. In this case, the braking pedal opening is small and its change rate is large, which indicates that the driver pays more attention to the braking safety during mode switching. Therefore, the upper limit of the change rate of the hydraulic braking torque takes a medium-large value.
Criterion 3: If is VL and is S, then is L. In this case, the braking pedal opening is very large and its change rate is small, indicating that the driver pays attention to both braking safety and ride comfort during mode switching, so the upper limit of the change rate of the hydraulic braking torque takes a large value.
According to the modified target hydraulic braking torque , the hydraulic controller determines the duty ratio of high-speed on–off valve, and directly controls the inlet valve and outlet valve of wheel cylinder through PWM modulation, so as to make the tracking pressure of wheel cylinders follow the modified target pressure changes.
4.2.2. The Modification of Target Motor Braking Torque
According to the analysis in
Section 3.3 of this paper, the response time of the MBS is shorter than that of the HBS, thus the rapid response of MBS can be used to compensate for the insufficient braking torque caused by the slow response of HBS, so as to solve the fluctuation of total braking torque and the jerk of the complete vehicle during brake mode switching. Therefore, during mode switching, the MBS need to provide the target motor brake torque
, which is determined by the braking force distribution controller and additionally provide the difference between the target hydraulic braking torque
and the current actual hydraulic braking torque
; that is,
The sum of target hydraulic braking torque
and target motor braking torque
is the total braking torque
required by the driver, so Equation (15) can be rewritten as
The motor control parameters and are output by the motor controller according to the modified target motor braking torque , so that the MBS outputs the actual motor braking torque to act on the vehicle.
According to the braking force distribution control strategy of this paper, the HBS starts to provide braking torque when the braking strength required by driver is greater than . If the braking torque required by driver changes, in order to maintain the coordinated compensation ability of the MBS to the hydraulic braking torque during mode switching, the target braking torque allocated by the braking force distribution controller to the MBS should be smaller than the maximum braking torque that can be provided by the MBS. When the braking torque required by the driver continues to increase, and the required braking strength satisfy , the target braking torque determined by braking force distribution controller should increase to gradually. If the braking torque required by driver remains unchanged, the maximum braking torque that can be provided by the MBS remains at at the braking torque distribution stage.