Online State-of-Charge Estimation Based on the Gas–Liquid Dynamics Model for Li(NiMnCo)O2 Battery
Abstract
:1. Introduction
1.1. Contribution of This Paper
1.2. Organization of This Paper
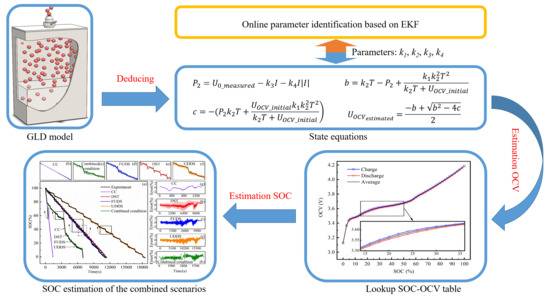
2. Identification of Battery Model Parameters
2.1. Battery Modelling
2.2. Offline Parameters Identification
2.3. Online Parameters Identification by Extended Kalman Filter (EKF)
2.4. Combination of Offline Parameters and Online Parameters for SOC Estimation
- (1)
- InitializationThe covariance between the true value and the best estimate at the initial time:All parameters in physical equations have actual physical meaning, so all parameters are non-negative including .and they cannot be initialized to be zero. Therefore, the initial parameters for online identification are set to close to zero which is (0.001,0.001,0.001,0.001). Additionally, step k is set as 1.
- (2)
- AssignmentThe current electron flow, terminal voltage and ambient temperature could be obtained by corresponding sensors at step k, noted as, . These three variables are assigned to corresponding variables and , respectively.
- (3)
- Calculation 1According to Equation (17) and offline parameters in Section 4.1, the estimated open-circuit voltage :Then, is set as one of the inputs to obtain estimated terminal voltage :Afterwards, the Jacobian matrix could be given by:
- (4)
- PredictionThe discrete Kalman filter predictions for the online parameters and covariance between the true value and the predicted value:
- (5)
- UpdateAccording to the prior state estimate and estimated covariance calculated in (4), the updates for the Kalman gain , posteriori state estimate , the covariance between the true value and the best estimate are given by:
- (6)
- Calculation 2Using the best estimate of the parameters as one of the inputs of Equation (16), the best estimate of the open-circuit voltage could be obtained:
- (7)
- Look-up tableAccording to the relationship between the SOC and OCV, the SOC at a specific OCV can be obtained by looking up the table.The flowchart of the joint SOC estimation algorithm is shown in Figure 2.
3. Experimental Details
3.1. Experimental Setup
3.2. Battery Tests
3.2.1. Hybrid Pulse Power Characterization
- (1)
- Capacity calibration: a LIB is completely discharged by 1 C constant current with the cut-off voltage of 3.0 V, charged under 1 C constant current until the voltage reaches 4.2 V, and then turned to 4.2 V constant voltage charge with the cut-off current of 1/20 C. This step is circulated three times. The calibration capacity is the average of the capacities under the three tests.
- (2)
- OCV data: the load time t, C-rate l and count N are ruled in Equation (56).After finishing a one-time load, the LIB is switched into the open-circuit condition for six hours.
- (3)
- Step 2 is repeated N times under the charge or discharge process. These experimental data are used to identify the offline parameters of the model and determined the SOC vs. OCV curve. Figure 4 shows the test results of HPPC when N and l are equal to 50 and 2 C, respectively. The OCV vs. SOC curves under the charge and discharge almost coincide. However, the large deviation between these two curves occurs at approximately SOC = 14–35% corresponding to the phase transition areas (LixCoO2, 0.75 < × < 0.93 is the mixed α + β phase) [39]. Although the extension of the standing time might reduce the deviation, this method is time-consuming. Alternatively, the more accurate OCV can be obtained by calculating their average values under the same SOC, as shown in the black curve (Figure 4).
3.2.2. Standard Tests and Combined Test
4. Results and Discussion
4.1. Model Offline Parameters Identification
4.2. Online SOC Estimation Based on Combined Online and Offline Parameter Identification
4.3. Analysis of the Sampling Time
4.4. Robustness Analysis of the Initial Value
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, J.; Wu, F.; Qiu, X.; Li, N.; Su, Y. Effect of CeO2-coating on the electrochemical performances of LiFePO4/C cathode material. Electrochim. Acta 2011, 56, 5587–5592. [Google Scholar] [CrossRef]
- Hoque, M.M.; Hannan, M.A.; Mohamed, A.; Ayob, A. Battery charge equalization controller in electric vehicle applications: A review. Renew. Sustain. Energy Rev. 2017, 75, 1363–1385. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery management systems in electric and hybrid vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Pattipati, B.; Pattipati, K.; Christopherson, J.P.; Namburu, S.M.; Prokhorov, D.V.; Qiao, L. Automotive Battery Management Systems; IEEE: Piscataway, NJ, USA, 2008; pp. 581–586. [Google Scholar] [CrossRef]
- Li, W.; Cao, D.; Jöst, D.; Ringbeck, F.; Kuipers, M.; Frie, F.; Sauer, D.U. Parameter sensitivity analysis of electrochemical model-based battery management systems for lithium-ion batteries. Appl. Energy 2020, 269, 115104. [Google Scholar] [CrossRef]
- Xia, B.; Lao, Z.; Zhang, R.; Tian, Y.; Chen, G.; Sun, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M.; et al. Online parameter identification and state of charge estimation of lithium-ion batteries based on forgetting factor recursive least squares and nonlinear Kalman filter. Energies 2018, 11, 3. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L.; Cai, Y.; Deng, H.; Sun, L. Online available capacity prediction and state of charge estimation based on advanced data-driven algorithms for lithium iron phosphate battery. Energy 2016, 112, 469–480. [Google Scholar] [CrossRef]
- Moya, A.A. Identification of characteristic time constants in the initial dynamic response of electric double layer capacitors from high-frequency electrochemical impedance. J. Power Sources 2018, 397, 124–133. [Google Scholar] [CrossRef]
- Liu, C.; Liu, W.; Wang, L.; Hu, G.; Ma, L.; Ren, B. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, L.; Zhu, J.; Wang, G.; Jiang, J. Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 2016, 180, 424–434. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part II: Pseudo-two-dimensional model simplification and state of charge estimation. J. Power Sources 2015, 278, 814–825. [Google Scholar] [CrossRef]
- Wang, Q.K.; He, Y.J.; Shen, J.N.; Hu, X.S.; Ma, Z.F. State of Charge-Dependent Polynomial Equivalent Circuit Modeling for Electrochemical Impedance Spectroscopy of Lithium-Ion Batteries. IEEE Trans. Power Electron. 2018, 33, 8449–8460. [Google Scholar] [CrossRef]
- Jiani, D.; Youyi, W.; Changyun, W. Li-ion battery SOC estimation using particle filter based on an equivalent circuit model. IEEE Int. Conf. Control Autom. 2013, 580–585. [Google Scholar] [CrossRef]
- Zhong, F.; Li, H.; Zhong, Q. An approach for SOC estimation based on sliding mode observer and fractional order equivalent circuit model of lithium-ion batteries. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 1497–1503. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Chen, Z. Kalman filter for onboard state of charge estimation and peak power capability analysis of lithium-ion batteries. J. Power Sources 2016, 328, 615–626. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, H.; Sun, H.; Yu, M.; Yang, J.; Li, H.; Wang, Y.; Chen, L.; Pan, C. A new gas–liquid dynamics model towards robust state of charge estimation of lithium-ion batteries. J. Energy Storage 2020, 29, 101343. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Liao, C.; Wang, L.; Xu, D. Recursive modeling and online identification of lithium-ion batteries for electric vehicle applications. Sci. China Technol. Sci. 2014, 57, 403–413. [Google Scholar] [CrossRef]
- Khare, N.; Chandra, S.; Govil, R. Statistical modeling of SoH of an automotive battery for online indication. In Proceedings of the INTELEC 2008—2008 IEEE 30th International Telecommunications Energy Conference, San Diego, CA, USA, 14–18 September 2008. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Wang, T.; Pei, L.; Lu, R.; Zhu, C.; Wu, G. Online parameter identification for lithium-ion cell in battery management system. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014. [Google Scholar] [CrossRef]
- Pei, L.; Zhu, C.; Wang, T.; Lu, R.; Chan, C.C. Online peak power prediction based on a parameter and state estimator for lithium-ion batteries in electric vehicles. Energy 2014, 66, 766–778. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on State of Charge estimation of batteries with adaptive extended kalman filter by experiment approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Wei, G.; Zhu, C. Online estimation of model parameters and state of charge of LiFePO4 batteries using a novel open-circuit voltage at various ambient temperatures. Energies 2015, 8, 2950–2976. [Google Scholar] [CrossRef] [Green Version]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Fu, Y.; Xu, J.; Gong, X. Online battery state of health estimation based on Genetic Algorithm for electric and hybrid vehicle applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- van Huysduynen, H.H.; Terken, J.; Martens, J.-B.; Eggen, B. Measuring driving styles: A validation of the multidimensional driving style inventory. In Proceedings of the 7th International Conference on Automotive User Interfaces and Interactive Vehicular Applications, Nottingham, UK, 1–3 September 2015; pp. 257–264. [Google Scholar]
- Du, Q.; Han, Q.; Zhang, Y.; Liu, Z.; Tian, S.; Zhang, Z. Adopting combined strategies to make state of charge (SOC) estimation for practical use. J. Renew. Sustain. Energy 2018, 10. [Google Scholar] [CrossRef]
- Li, J.; Barillas, J.K.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Sangwan, V.; Kumar, R.; Rathore, A.K. State-of-charge estimation for Li-ion battery using extended Kalman filter (EKF) and central difference Kalman filter (CDKF). In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Seo, B.H.; Nguyen, T.H.; Lee, D.C.; Lee, K.B.; Kim, J.M. Condition monitoring of lithium polymer batteries based on a sigma-point Kalman filter. J. Power Electron. 2012, 12, 778–786. [Google Scholar] [CrossRef]
- Movassagh, K.; Raihan, S.A.; Balasingam, B. Performance analysis of coulomb counting approach for state of charge estimation. In Proceedings of the 2019 IEEE Electrical Power and Energy Conference (EPEC), Montreal, QC, Canada, 16–18 October 2019; Volume 3, pp. 1–6. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Li, W.; Liang, L.; Liu, W.; Wu, X. State of Charge Estimation of Lithium-Ion Batteries Using a Discrete-Time Nonlinear Observer. IEEE Trans. Ind. Electron. 2017, 64, 8557–8565. [Google Scholar] [CrossRef]
- Hasan, A.; Skriver, M.; Johansen, T.A. Exogenous kalman filter for lithium-ion batteries state-of-charge estimation in electric vehicles. arXiv 2018, arXiv:1810.09014, 1403–1408. [Google Scholar]
- Isa, A.I.; Hamza, M.F. Effect of sampling time on PID controller design for a heat exchanger system. IEEE Int. Conf. Adapt. Sci. Technol. 2015. [Google Scholar] [CrossRef]
- Reimers, J.N.; Dahn, J.R. Electrochemical and In Situ X-Ray Diffraction Studies of Lithium Intercalation in Li x CoO2. J. Electrochem. Soc. 1992, 139, 2091–2097. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. Online estimation of model parameters and state-of-charge of Lithium-Ion battery using Unscented Kalman Filter. Proc. Am. Control Conf. 2012, 3962–3967. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness Evaluation of Extended and Unscented Kalman Filter for Battery State of Charge Estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar] [CrossRef]
- Wang, Q.; Kang, J.; Tan, Z.; Luo, M. An online method to simultaneously identify the parameters and estimate states for lithium ion batteries. Electrochim. Acta 2018, 289, 376–388. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, H.; Zou, C.; Li, Z.; Zhang, L. Co-Estimation of State of Charge and State of Health for Lithium-Ion Batteries Based on Fractional-Order Calculus. IEEE Trans. Veh. Technol. 2018, 67, 10319–10329. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Yang, D.; Chen, Z. An on-line estimation of battery pack parameters and state-of-charge using dual filters based on pack model. Energy 2016, 115, 219–229. [Google Scholar] [CrossRef]
- Hansen, T.; Wang, C.J. Support vector based battery state of charge estimator. J. Power Sources 2005, 141, 351–358. [Google Scholar] [CrossRef]
- Pattipati, B.; Balasingam, B.; Avvari, G.V.; Pattipati, K.R.; Bar-Shalom, Y. Open circuit voltage characterization of lithium-ion batteries. J. Power Sources 2014, 269, 317–333. [Google Scholar] [CrossRef]









| GLD Battery Model Parameters | Actual Battery Parameters |
|---|---|
| Pressure of gas at the nozzle | Terminal voltage |
| Gas flow velocity | Electron flow |
| Pressure of gas before opening the valve | Initial open-circuit voltage |
| Pressure of gas after rebalance | Estimated open-circuit voltage |
| Temperature in cans | Temperature of the battery |
| Condition | CC | DST | FUDS | UDDS | Combined Condition |
|---|---|---|---|---|---|
| MAE (%) | 0.50 | 0.43 | 0.39 | 0.35 | 0.49 |
| ME (%) | 1.59 | 2.50 | 2.02 | 2.42 | 2.51 |
| Reference | Estimation Technique | Model | Parameter Identification | Test Condition | MAE (%) |
|---|---|---|---|---|---|
| [40] | EKF | PNGV | Online | DST | <2.1 |
| [40] | UKF | PNGV | Online | DST | <1.05 |
| [41] | UKF | Combined | Offline | FUDS | 0.8 |
| [42] | RLS + EKF | 2RC | Online | FUDS | 1.1 |
| [43] | Dual UKF | 2RC | Online | DST | 0.29 |
| [44] | Dual EKF | 2RC | Online | FUDS | 0.34 |
| [45] | EKF + UKF | 2RC | Online | DST | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Chen, X.; Liu, Y.; Zhao, Q.; Li, H.; Chen, B. Online State-of-Charge Estimation Based on the Gas–Liquid Dynamics Model for Li(NiMnCo)O2 Battery. Energies 2021, 14, 324. https://doi.org/10.3390/en14020324
Jiang H, Chen X, Liu Y, Zhao Q, Li H, Chen B. Online State-of-Charge Estimation Based on the Gas–Liquid Dynamics Model for Li(NiMnCo)O2 Battery. Energies. 2021; 14(2):324. https://doi.org/10.3390/en14020324
Chicago/Turabian StyleJiang, Haobin, Xijia Chen, Yifu Liu, Qian Zhao, Huanhuan Li, and Biao Chen. 2021. "Online State-of-Charge Estimation Based on the Gas–Liquid Dynamics Model for Li(NiMnCo)O2 Battery" Energies 14, no. 2: 324. https://doi.org/10.3390/en14020324
APA StyleJiang, H., Chen, X., Liu, Y., Zhao, Q., Li, H., & Chen, B. (2021). Online State-of-Charge Estimation Based on the Gas–Liquid Dynamics Model for Li(NiMnCo)O2 Battery. Energies, 14(2), 324. https://doi.org/10.3390/en14020324