Performance Assessment of Global Horizontal Irradiance Models in All-Sky Conditions
Abstract
:1. Introduction
2. Data Collection
- ;
- ;
- .
- Visible (0.67 μm);
- Shortwave infrared (3.7 μm);
- Water vapor (6.7 μm);
- Infrared (10.8 μm);
- Infrared (12.0 μm).
3. Global Horizontal Irradiance Estimation
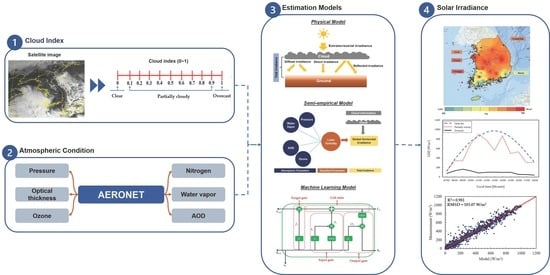
3.1. Cloud Estimation
3.2. FARMS
3.3. LSTM
3.4. Hammer Model
3.5. Model Performance Criteria
4. Result Analysis
5. Conclusions
- Compared to the Hammer model, the FARMS provides a more precise estimation because the FARMS takes advantage of more detailed information of atmospheric conditions. On the other hand, the Hammer model is more accessible since the input parameters are fewer and commonly measured by an open-access organization.
- In general, the LSTM outperforms the FARMS and the Hammer model in estimating GHI. In comparison to the slight improvement in rRMSD, the improvement in rMBD by the LSTM is significant. The rMBD value less than 1% indicates that long-term means of GHI can be accurately estimated.
- The LSTM using the FARMS input parameters produces the best accuracy, with a difference in rRMSD of 4.44% compared to its Hammer model counterpart.
- Based on the climate, the FARMS was subjected to considerable bias and error in locations with a temperate, dry winter, and hot summer climate due to the distinct seasonal fluctuations. On the other hand, the Hammer model tends to overestimate in the cities with no dry season since the value of precipitable water varies. Conversely, the LSTM was primarily unaffected by the change in climate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Air mass | |
| Cloud index | |
| Satellite pixel value | |
| Normalized satellite pixel value | |
| Raw satellite pixel value | |
| Extraterrestrial irradiance | |
| Clearness index | |
| Local pressure, hPa | |
| Temperature, °C | |
| Linke turbidity | |
| Ozone, atm-cm | |
| Optical thickness, cm | |
| Nitrogen, atm-cm | |
| Precipitable water, cm | |
| Greek Symbols | |
| Backscattering angle, deg | |
| Satellite zenith angle, deg | |
| Solar zenith angle, deg | |
| Normalized variation of the sun-to-earth distance from its mean value | |
| Albedo | |
| Rayleigh optical thickness | |
| Angstrom coefficient | |
| Angstrom turbidity | |
| Subscripts | |
| Clear case | |
| Cloudy case | |
| Abbreviations | |
| Diffuse Horizontal Irradiance, W/m2 | |
| Direct Normal Irradiance, W/m2 | |
| Global Horizontal Irradiance, W/m2 | |
| Recurrent Neural Network | |
| Long Short-Term Memory | |
| Mean Bias Differences (W/m2) | |
| Root Mean Square Differences (W/m2) | |
| Relative Mean Bias Differences (%) | |
| Relative Root Mean Square Differences (%) | |
| Fast All-sky Radiation Model for Solar applications | |
| Radiative Transfer | |
| Korea Meteorological Administration | |
| Communication, Ocean, and Meteorological Satellite | |
| The National Aeronautics and Space Administration |
References
- Inman, R.H.; Pedro, H.; Coimbra, C.F. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. (Eds.) Solar Engineering of Thermal Processes, 4th ed.; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-1-118-41541-2. [Google Scholar]
- Kleissl, J. Solar Energy Forecasting and Resource Assessment; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Paudel, I.; Cohen, S.; Stanhill, G. The Role of Clouds in Global Radiation Changes Measured in Israel during the Last Sixty Years. Am. J. Clim. Chang. 2019, 8, 61–76. [Google Scholar] [CrossRef] [Green Version]
- Lappalainen, K.; Valkealahti, S. Recognition and modelling of irradiance transitions caused by moving clouds. Sol. Energy 2015, 112, 55–67. [Google Scholar] [CrossRef]
- Zelenka, A.; Perez, R.; Seals, R.; Renné, D. Effective Accuracy of Satellite-Derived Hourly Irradiances. Theor. Appl. Clim. 1999, 62, 199–207. [Google Scholar] [CrossRef]
- Mouhamet, D.; Tommy, A.; Primerose, A.; Laurent, L. Improving the Heliosat-2 method for surface solar irradiation estimation under cloudy sky areas. Sol. Energy 2018, 169, 565–576. [Google Scholar] [CrossRef]
- Kim, B.-Y.; Cha, J. Cloud Observation and Cloud Cover Calculation at Nighttime Using the Automatic Cloud Observation System (ACOS) Package. Remote. Sens. 2020, 12, 2314. [Google Scholar] [CrossRef]
- Kim, C.K.; Kim, H.-G.; Kang, Y.-H.; Yun, C.-Y. Toward Improved Solar Irradiance Forecasts: Comparison of the Global Horizontal Irradiances Derived from the COMS Satellite Imagery Over the Korean Peninsula. Pure Appl. Geophys. 2017, 174, 2773–2792. [Google Scholar] [CrossRef]
- Mommert, M. Cloud Identification from All-sky Camera Data with Machine Learning. Astron. J. 2020, 159, 178. [Google Scholar] [CrossRef]
- Huo, J.; Lu, D. Cloud Determination of All-Sky Images under Low-Visibility Conditions. J. Atmos. Ocean. Technol. 2009, 26, 2172–2181. [Google Scholar] [CrossRef]
- Wacker, S.; Gröbner, J.; Zysset, C.; Diener, L.; Tzoumanikas, P.; Kazantzidis, A.; Vuilleumier, L.; Stöckli, R.; Nyeki, S.; Kämpfer, N. Cloud observations in Switzerland using hemispherical sky cameras. J. Geophys. Res. Atmos. 2015, 120, 695–707. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Zhang, L.; Zhang, Z.; Wang, C.; Xiao, B. Automatic Cloud Detection for All-Sky Images Using Superpixel Segmentation. IEEE Geosci. Remote. Sens. Lett. 2014, 12, 354–358. [Google Scholar] [CrossRef]
- Kim, B.-Y.; Jee, J.-B.; Zo, I.-S.; Lee, K.-T. Cloud cover retrieved from skyviewer: A validation with human observations. Asia-Pac. J. Atmos. Sci. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Moore, K.; Kmiecik, M.; Chain, C.; George, R.; Vignola, F. A new operational model for satellite-derived irradiances: Description and validation. Sol. Energy 2002, 73, 307–317. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Perez, R.; Seals, R.; Zelenka, A. Comparing satellite remote sensing and ground network measurements for the production of site/time specific irradiance data. Sol. Energy 1997, 60, 89–96. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Ingram, W.; Tsushima, Y.; Satoh, M.; Roberts, M.; Vidale, P.L.; O’Gorman, P.A. Relative humidity changes in a warmer climate. J. Geophys. Res. Atmos. 2010, 115, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Rubel, F.; Brugger, K.; Haslinger, K.; Auer, I. The climate of the European Alps: Shift of very high resolution Köppen-Geiger climate zones 1800–2100. Meteorol. Z. 2017, 26, 115–125. [Google Scholar] [CrossRef]
- Köppen, W. The thermal zones of the Earth according to the duration of hot, moderate and cold periods and to the impact of heat on the organic world. Meteorol. Z. 2011, 20, 351–360. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]
- Qingyuan, Z.; Huang, J.; Siwei, L. Development of Typical Year Weather Data for Chinese Locations. ASHRAE Trans. 2002, 108, 1063–1075. [Google Scholar]
- Hu, Y.X.; Stamnes, K. An accurate parameterization of the radiative properties of water clouds suitable for use in climate models. J. Clim. 1993, 6, 728–742. [Google Scholar] [CrossRef] [Green Version]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Space Phys. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Berk, A.; Bernstein, L.; Anderson, G.; Acharya, P.; Robertson, D.; Chetwynd, J.; Adler-Golden, S. MODTRAN Cloud and Multiple Scattering Upgrades with Application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Xie, Y.; Sengupta, M.; Dudhia, J. A Fast All-sky Radiation Model for Solar applications (FARMS): Algorithm and performance evaluation. Sol. Energy 2016, 135, 435–445. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.K.; Kim, H.-G.; Kang, Y.-H.; Yun, C.-Y.; Lee, S.-N. Evaluation of Global Horizontal Irradiance Derived from CLAVR-x Model and COMS Imagery Over the Korean Peninsula. New Renew. Energy 2016, 12, 13–20. [Google Scholar] [CrossRef]
- Fu, C.-L.; Cheng, H.-Y. Predicting solar irradiance with all-sky image features via regression. Sol. Energy 2013, 97, 537–550. [Google Scholar] [CrossRef]
- Hammer, A.; Heinemann, D.; Hoyer, C.; Kuhlemann, R.; Lorenz, E.; Müller, R.; Beyer, H.G. Solar energy assessment using remote sensing technologies. Remote. Sens. Environ. 2003, 86, 423–432. [Google Scholar] [CrossRef]
- Rigollier, C.; Lefèvre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Aslam, M.; Lee, J.-M.; Kim, H.-S.; Lee, S.-J.; Hong, S. Deep Learning Models for Long-Term Solar Radiation Forecasting Considering Microgrid Installation: A Comparative Study. Energies 2019, 13, 147. [Google Scholar] [CrossRef] [Green Version]
- Ramadhan, R.A.; Heatubun, Y.R.; Tan, S.F.; Lee, H.-J. Comparison of physical and machine learning models for estimating solar irradiance and photovoltaic power. Renew. Energy 2021, 178, 1006–1019. [Google Scholar] [CrossRef]
- Garniwa, P.M.P.; Ramadhan, R.A.A.; Lee, H.-J. Application of Semi-Empirical Models Based on Satellite Images for Estimating Solar Irradiance in Korea. Appl. Sci. 2021, 11, 3445. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Ruiz-Arias, J.A. Extensive worldwide validation and climate sensitivity analysis of direct irradiance predictions from 1-min global irradiance. Sol. Energy 2016, 128, 1–30. [Google Scholar] [CrossRef]
- Lave, M.; Hayes, W.; Pohl, A.; Hansen, C.W. Evaluation of Global Horizontal Irradiance to Plane-of-Array Irradiance Models at Locations Across the United States. IEEE J. Photovolt. 2015, 5, 597–606. [Google Scholar] [CrossRef]
- Komhyr, W.D.; Grass, R.D.; Leonard, R.K. Dobson spectrophotometer 83: A standard for total ozone measurements, 1962–1987. J. Geophys. Res. Space Phys. 1989, 94, 9847–9861. [Google Scholar] [CrossRef]
- Mcpeters, R.D.; Bhartia, P.K.; Krueger, A.J.; Herman, J.R.; Wellemeyer, C.G.; Seftor, C.J.; Jaross, G.; Schlesinger, B.M.; Torres, O.; Labow, G.; et al. Earth Probe Total Ozone Mapping Spectrometer (TOMS) Data; NASA Technical Publication: Greenbelt, MD, USA, 1996.
- Levelt, P.F.; Van Den Oord, G.H.J.; Dobber, M.R.; Malkki, A.; Visser, H.; De Vries, J.; Stammes, P.; Lundell, J.O.V.; Saari, H. The ozone monitoring instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1093–1101. [Google Scholar] [CrossRef]
- Holben, B.; Eck, T.; Slutsker, I.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.; Kaufman, Y.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Holben, B.N.; Tanré, D.; Smirnov, A.; Eck, T.F.; Slutsker, I.; Abuhassan, N.; Newcomb, W.W.; Schafer, J.S.; Chatenet, B.; Lavenu, F.; et al. An emerging ground-based aerosol climatology: Aerosol optical depth from AERONET. J. Geophys. Res. Space Phys. 2001, 106, 12067–12097. [Google Scholar] [CrossRef]
- Kasten, F.; Young, A.T. Revised optical air mass tables and approximation formula. Appl. Opt. 2000, 28, 4735–4738. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sedlacek, A.J.; DeSá, S.S.; Martin, S.T.; Alexander, M.L.; Alexander, M.L.; Watson, T.B.; Aiken, A.C.; Springston, S.R.; Artaxo, P. Deriving brown carbon from multiwavelength absorption measurements: Method and application to AERONET and Aethalometer observations. Atmos. Chem. Phys. 2016, 16, 12733–12752. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gueymard, C.A. REST2: High-performance solar radiation model for cloudless-sky irradiance, illuminance, and photosynthetically active radiation—Validation with a benchmark dataset. Sol. Energy 2008, 82, 272–285. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.; Lee, H.-J. A Review on Deep Learning Models for Forecasting Time Series Data of Solar Irradiance and Photovoltaic Power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Kim, H.Y.; Won, C.H. Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH-type models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Paola, J.D.; Schowengerdt, R.A. A review and analysis of backpropagation neural networks for classification of remotely-sensed multi-spectral imagery. Int. J. Remote Sens. 1995, 16, 3033–3058. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, L.; Hou, C.; Han, H.; Liu, Z.; Sun, Y.; Zheng, M. Wind Power Short-Term Prediction Based on LSTM and Discrete Wavelet Transform. Appl. Sci. 2019, 9, 1108. [Google Scholar] [CrossRef] [Green Version]
- Remund, J.; Wald, L.; Lefèvre, M.; Ranchin, T.; Page, J. Worldwide Linke Turbidity Information. ISES 2003, 400, 13–26. [Google Scholar] [CrossRef] [Green Version]









| Reference | Year | Area | Köppen–Geiger Classification | Number of Locations | Model | RMSD (W/m2) | rRMSD (%) |
|---|---|---|---|---|---|---|---|
| Xie et al. [27] | 2016 | United States | Temperate (Cfa) | 1 | Physical | 130 | - |
| Kim et al. [28] | 2016 | Korea | Continental (Dwa) | 4 | Physical | 146 | 57 |
| Fu et al. [29] | 2016 | Asia | Temperate (Cfa) | 1 | Physical | 169 | - |
| Hammer et al. [30] | 2003 | Europe | Temperate (Cfa Cfb, Cfc, Csa, Csb) Continental (Dfa, Dfb) | 1 | Semi-empirical | - | 35 |
| Perez et al. [15] | 2002 | United States | Temperate (All subtypes) Continental (All subtypes) | 10 | Semi-empirical | 118 | - |
| Rigollier et al. [31] | 2004 | Europe | Temperate (Cfa, Cfb, Cfc, Csa, Csb) Continental (Dfa, Dfb) | 35 | Semi-empirical | - | 45 |
| Aslam et al. [32] | 2019 | Korea | Temperate (Cwa) | 2 | Machine learning | 113 | - |
| Ramadhan et al. [33] | 2021 | Korea | Temperate (Cwa) | 1 | Machine learning | 102 | 26 |
| Garniwa et al. [34] | 2021 | Korea | Temperate (Cwa) | 1 | Machine learning | 76 | 21 |
| Station Name | Locations | Köppen-Geiger Climate |
|---|---|---|
| Seoul | 37.4580° N, 126.9511° E | Cold, dry winter, hot summer (Dwa) |
| Gangneung | 37.7710° N, 128.8670° E | Cold, no dry season, hot summer (Dfa) |
| Gwangju | 35.2282° N, 126.8431° E | Temperate, no dry season, hot summer (Cfa) |
| Seosan | 36.5385° N, 126.3301° E | Temperate, dry winter, hot summer (Cwa) |
| Busan | 37.3388° N, 127.2658° E | Temperate, dry winter, hot summer (Cwa) |
| Model | Data Input |
|---|---|
| FARMS | , , , , , , , , |
| Hammer | , , , , |
| LSTM-FARMS | , , , , , , , , |
| LSTM-Hammer | , , , , |
| Location | Model | RMSD (W/m2) | rRMSD (%) | MBD (W/m2) | rMBD (%) |
|---|---|---|---|---|---|
| Seoul | FARMS | 125.34 | 32.06 | 18.14 | 4.64 |
| LSTM-FARMS | 100.64 | 25.74 | 0.54 | 0.14 | |
| Hammer | 119.65 | 30.61 | 34.28 | 8.77 | |
| LSTM-Hammer | 114.39 | 29.26 | 9.85 | 2.52 | |
| Gangneung | FARMS | 134.23 | 31.57 | 11.95 | 2.81 |
| LSTM-FARMS | 103.07 | 24.24 | 2.38 | 0.56 | |
| Hammer | 136.14 | 32.02 | 36.22 | 8.52 | |
| LSTM-Hammer | 121.85 | 28.66 | 9.69 | 2.28 | |
| Seosan | FARMS | 148.75 | 33.57 | 4.53 | 1.02 |
| LSTM-FARMS | 114.40 | 25.82 | 1.46 | 0.33 | |
| Hammer | 138.64 | 31.29 | 18.87 | 4.26 | |
| LSTM-Hammer | 124.29 | 28.05 | 2.53 | 0.57 | |
| Gwangju | FARMS | 140.19 | 32.52 | 13.58 | 3.15 |
| LSTM-FARMS | 102.26 | 23.72 | 3.84 | 0.89 | |
| Hammer | 141.29 | 32.78 | 37.80 | 8.77 | |
| LSTM-Hammer | 123.33 | 28.61 | 7.55 | 1.75 | |
| Busan | FARMS | 146.37 | 32.78 | 32.82 | 7.35 |
| LSTM-FARMS | 110.60 | 24.77 | 5.49 | 1.23 | |
| Hammer | 130.91 | 29.32 | 32.68 | 7.32 | |
| LSTM-Hammer | 130.43 | 29.21 | 4.55 | 1.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamil, R.; Garniwa, P.M.P.; Lee, H. Performance Assessment of Global Horizontal Irradiance Models in All-Sky Conditions. Energies 2021, 14, 7939. https://doi.org/10.3390/en14237939
Kamil R, Garniwa PMP, Lee H. Performance Assessment of Global Horizontal Irradiance Models in All-Sky Conditions. Energies. 2021; 14(23):7939. https://doi.org/10.3390/en14237939
Chicago/Turabian StyleKamil, Raihan, Pranda M. P. Garniwa, and Hyunjin Lee. 2021. "Performance Assessment of Global Horizontal Irradiance Models in All-Sky Conditions" Energies 14, no. 23: 7939. https://doi.org/10.3390/en14237939
APA StyleKamil, R., Garniwa, P. M. P., & Lee, H. (2021). Performance Assessment of Global Horizontal Irradiance Models in All-Sky Conditions. Energies, 14(23), 7939. https://doi.org/10.3390/en14237939