On Optimistic and Pessimistic Bilevel Optimization Models for Demand Response Management
Abstract
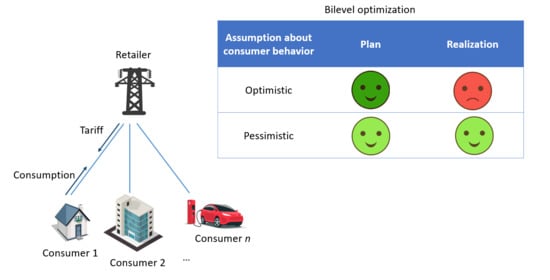
:1. Introduction
2. Literature Review
3. Problem Definition
4. Preliminaries
4.1. The Continuous Knapsack Problem
- 1.
- for , for ;
- 2.
- .
4.2. General Properties of Optimal Solutions
- for ;
- ;
- ;
- ;
- .
5. Polynomially Solvable Special Cases with One Consumer Only
5.1. The Optimistic Variant
- If , then , and is decreased by , while is increased by for all , where .
- If , then , and is increased by , while increases by for all , where .
5.2. The Pessimistic Variant
6. The General Case with Multiple Consumers
6.1. Solution of the General Optimistic Variant
6.2. Solution of the General Pessimistic Variant
- Either , or
- , and for .
- ;
- If for some , then ;
- If for some , then ;
- If then , and
- If then for each follower i.
- If , then and the order of the two time periods does not change.
- If and then three cases can be distinguished:
- -
- If and then . Hence, the order of periods and will change for in order to satisfy the optimality conditions.
- -
- If and then . Hence, the order of and will not change for .
- -
- If , then the order of and will not change for .
| Algorithm 1. Pessimistic Solution |
|
7. Experimental Evaluation
7.1. Numerical Example
7.2. Computational Experiments
8. Conclusions and Managerial Implications
8.1. Managerial Implications
8.2. Directions for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- de Souza Dutra, M.D.; Alguacil, N. Optimal residential users coordination via demand response: An exact distributed framework. Appl. Energy 2020, 279, 115851. [Google Scholar] [CrossRef]
- Kovács, A. Bilevel programming approach to demand response management with day-ahead tariff. J. Mod. Power Syst. Clean Energy 2019, 7, 1632–1643. [Google Scholar] [CrossRef] [Green Version]
- Wei, W.; Liu, F.; Mei, S. Energy Pricing and Dispatch for Smart Grid Retailers Under Demand Response and Market Price Uncertainty. IEEE Trans. Smart Grid 2015, 6, 1364–1374. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. Supply-demand balancing for power management in smart grid: A Stackelberg game approach. Appl. Energy 2016, 164, 702–710. [Google Scholar] [CrossRef]
- Zugno, M.; Morales, J.M.; Pinson, P.; Madsen, H. A bilevel model for electricity retailers’ participation in a demand response market environment. Energy Econ. 2013, 36, 182–197. [Google Scholar] [CrossRef]
- Dempe, S. Foundations of Bilevel Programming; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Cupelli, L.; Schumacher, M.; Monti, A.; Mueller, D.; De Tommasi, L.; Kouramas, K. Simulation Tools and Optimization Algorithms for Efficient Energy Management in Neighborhoods. In Energy Positive Neighborhoods and Smart Energy Districts; Monti, A., Pesch, D., Ellis, K., Mancarella, P., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 57–100. [Google Scholar]
- Bracken, J.; McGill, J.T. Mathematical programs with optimization problems in the constraints. Oper. Res. 1973, 21, 37–44. [Google Scholar] [CrossRef]
- Bard, J.F. Practical Bilevel Optimization: Algorithms and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1998. [Google Scholar]
- Colson, B.; Marcotte, P.; Savard, G. An overview of bilevel optimization. Ann. Oper. Res. 2007, 153, 235–256. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bard, J.F.; Falk, J.E. An explicit solution to the multi-level programming problem. Comput. Oper. Res. 1982, 9, 77–100. [Google Scholar] [CrossRef]
- Ye, J.; Zhu, D. Optimality conditions for bilevel programming problems. Optimization 1995, 33, 9–27. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.J.; Zhu, D. New necessary optimality conditions for bilevel programs by combining the MPEC and value function approaches. SIAM J. Optim. 2010, 20, 1885–1905. [Google Scholar] [CrossRef]
- Dempe, S.; Mordukhovich, B.S.; Zemkoho, A.B. Necessary optimality conditions in pessimistic bilevel programming. Optimization 2014, 63, 505–533. [Google Scholar] [CrossRef]
- Dempe, S.; Mordukhovich, B.S.; Zemkoho, A.B. Two-level value function approach to non-smooth optimistic and pessimistic bilevel programs. Optimization 2019, 68, 433–455. [Google Scholar] [CrossRef] [Green Version]
- Zeng, B. A Practical Scheme to Compute the Pessimistic Bilevel Optimization Problem. INFORMS J. Comput. 2020, 32, 1128–1142. [Google Scholar] [CrossRef]
- Dempe, S.; Kalashnikov, V.; Pérez-Valdés, G.A.; Kalashnykova, N. Bilevel Programming Problems: Theory, Algorithms and Applications to Energy Networks; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ben-Ayed, O. Bilevel linear programming. Comput. Oper. Res. 1993, 20, 485–501. [Google Scholar] [CrossRef]
- Lozano, L.; Smith, J.C. A value-function-based exact approach for the bilevel mixed-integer programming problem. Oper. Res. 2017, 65, 768–786. [Google Scholar] [CrossRef]
- Brotcorne, L.; Labbé, M.; Marcotte, P.; Savard, G. A bilevel model and solution algorithm for a freight tariff-setting problem. Transp. Sci. 2000, 34, 289–302. [Google Scholar] [CrossRef] [Green Version]
- Loridan, P.; Morgan, J. Weak via strong Stackelberg problem: New results. J. Glob. Optim. 1996, 8, 263–287. [Google Scholar] [CrossRef]
- Wiesemann, W.; Tsoukalas, A.; Kleniati, P.M.; Rustem, B. Pessimistic bilevel optimization. SIAM J. Optim. 2013, 23, 353–380. [Google Scholar] [CrossRef]
- Kovács, A. On the Computational Complexity of Tariff Optimization for Demand Response Management. IEEE Trans. Power Syst. 2018, 33, 3204–3206. [Google Scholar] [CrossRef] [Green Version]
- Wei, F.; Jing, Z.; Wu, P.Z.; Wu, Q. A Stackelberg game approach for multiple energies trading in integrated energy systems. Appl. Energy 2017, 200, 315–329. [Google Scholar] [CrossRef]
- Yoon, A.Y.; Kang, H.K.; Moon, S.I. Optimal Price Based Demand Response of HVAC Systems in Commercial Buildings Considering Peak Load Reduction. Energies 2020, 13, 862. [Google Scholar] [CrossRef] [Green Version]
- Jalali, M.; Zare, K.; Seyedi, H. Strategic decision-making of distribution network operator with multi-microgrids considering demand response program. Energy 2017, 141, 1059–1071. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Nguyen, H.T.; Le, L.B. Dynamic Pricing Design for Demand Response Integration in Power Distribution Networks. IEEE Trans. Power Syst. 2016, 31, 3457–3472. [Google Scholar] [CrossRef]
- Soliman, H.; Leon-Garcia, A. Game-Theoretic Demand-Side Management With Storage Devices for the Future Smart Grid. IEEE Trans. Smart Grid 2014, 5, 1475–1485. [Google Scholar] [CrossRef]
- Song, X.; Lin, H.; De, G.; Li, H.; Fu, X.; Tan, Z. An Energy Optimal Dispatching Model of an Integrated Energy System Based on Uncertain Bilevel Programming. Energies 2020, 13, 477. [Google Scholar] [CrossRef] [Green Version]
- Vardanyan, Y.; Madsen, H. Stochastic Bilevel Program for Optimal Coordinated Energy Trading of an EV Aggregator. Energies 2019, 12, 3813. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Zhang, S.; Wang, X.; Li, X.; Wu, L. Conditional-Robust-Profit-Based Optimization Model for Electricity Retailers with Shiftable Demand. Energies 2020, 13, 1308. [Google Scholar] [CrossRef] [Green Version]
- Alves, M.J.; Antunes, C.H. A semivectorial bilevel programming approach to optimize electricity dynamic time-of-use retail pricing. Comput. Oper. Res. 2018, 92, 130–144. [Google Scholar] [CrossRef]






| t | 1 | 2 |
|---|---|---|
| 10 | 50 | |
| 20 | 20 | |
| 40 | 40 | |
| 10 | 30 | |
| 0 | 0 | |
| 1 | 1 |
| t | 1 | 2 |
|---|---|---|
| 10 | 50 | |
| 20 | 20 | |
| 40 | 40 | |
| 40 | 40 | |
| 0 | 0 | |
| 1 | 1 |
| m | T | Opt | Time [s] | Gap [%] | |
|---|---|---|---|---|---|
| Avg. | Max. | ||||
| 5 | 12 | 10 | 0.08 | - | - |
| 24 | 10 | 0.16 | - | - | |
| 36 | 10 | 0.72 | - | - | |
| 48 | 10 | 1.40 | - | - | |
| 10 | 12 | 10 | 0.28 | - | - |
| 24 | 10 | 2.73 | - | - | |
| 36 | 10 | 5.06 | - | - | |
| 48 | 10 | 13.92 | - | - | |
| 15 | 12 | 10 | 1.83 | - | - |
| 24 | 10 | 6.01 | - | - | |
| 36 | 10 | 30.85 | - | - | |
| 48 | 10 | 47.88 | - | - | |
| 20 | 12 | 10 | 4.39 | - | - |
| 24 | 8 | 81.29 | 0.58 | 5.34 | |
| 36 | 9 | 66.10 | 0.20 | 2.03 | |
| 48 | 7 | 172.74 | 1.37 | 12.76 | |
| 25 | 12 | 10 | 5.00 | - | - |
| 24 | 5 | 185.13 | 0.90 | 3.41 | |
| 36 | 5 | 250.15 | 2.12 | 11.81 | |
| 48 | 5 | 203.51 | 13.11 | 100.00 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kis, T.; Kovács, A.; Mészáros, C. On Optimistic and Pessimistic Bilevel Optimization Models for Demand Response Management. Energies 2021, 14, 2095. https://doi.org/10.3390/en14082095
Kis T, Kovács A, Mészáros C. On Optimistic and Pessimistic Bilevel Optimization Models for Demand Response Management. Energies. 2021; 14(8):2095. https://doi.org/10.3390/en14082095
Chicago/Turabian StyleKis, Tamás, András Kovács, and Csaba Mészáros. 2021. "On Optimistic and Pessimistic Bilevel Optimization Models for Demand Response Management" Energies 14, no. 8: 2095. https://doi.org/10.3390/en14082095
APA StyleKis, T., Kovács, A., & Mészáros, C. (2021). On Optimistic and Pessimistic Bilevel Optimization Models for Demand Response Management. Energies, 14(8), 2095. https://doi.org/10.3390/en14082095