1. Introduction
The important and currently up-to-date steps aimed at rational energy use require optimization of technological installations in terms of energy demand, mainly electricity or heat. Actions taken in this area involve both existing installations, as well as new, redesigned, or significantly upgraded installations. If they are used to carry out processes on liquid substances, their indispensable elements include systems dedicated to pumping substrates, semi-finished products, and final products. It is often the case that the energy consumption of a given technological operation is not determined by the course of the process carried out in a specific apparatus, but by the energy necessary to provide it with the appropriate volume or mass flow rates of process fluids. We can mention installations used for the implementation of heat or mass transfer as an example, although pipeline fluid conveying systems form the most common examples in this area.
The process fluid feeding systems primarily include pumps. Their design is diverse, as it often depends on the specific properties of the substances that need to be pumped. In practice, these are not single-component homogeneous liquids, but multi-component solutions or multiphase mixtures. Regardless of the principle of operation of such pumps, the energy required for its correct operation is directly related to the demand for pumping power. As we know, this power results from the product of the flow rate of the substance flow and the overpressure generated by the pump that is necessary to overcome certain flow resistance. It is also worth recalling that the mechanical performance of a pump does not depend on the phenomena that occur in the pipeline.
Therefore, efforts made to reduce the demand for energy required to pump a substance need to involve measures taken with the purpose of drag reduction in the pipes of process installations. It is of particular importance when these are substances with high viscosities. It is assumed that their viscosity is 100 times greater than that of water, which practically eliminates all gases and vapors from this group. However, there are a large number of various liquids and solutions and multiphase systems. In this respect, petroleum-derived substances attract particular interest in research. These are hydrophobic liquids with a complex composition and high viscosity, whose pumping in pipes of technological installations requires a significant input of energy.
The reduction of the pressure losses of the liquid flowing in a pipe of a certain diameter and length is possible only by reducing inherent forces developed in it, which are the reaction of the substance to its strain rate. The value of these forces results directly from the phenomenon of inherent friction, i.e., fluid viscosity. Thus, an effective way to lower the energy required to pump any liquid would be to lower its viscosity, which is easily accomplished by increasing the temperature. However, such an action is not commonly technically viable, and besides, it generates a considerable demand for another form of energy, i.e., heat.
The outcomes related to lowering the drag resistance of liquid substances can be more feasibly obtained using surfactants. With regard to conveying highly viscous petroleum liquids or permanent emulsions in a pipeline, the essence of such activities and a description of its results is reported by Zaki [
1], Mowla and Naderi [
2], as well as Gillies et al. [
3]. These studies indicate that the presence of appropriately selected surfactants can reduce the shear stresses on the pipe wall, and thus the flow resistance. However, the type of pipe material and the condition of its surface are important, as clearly indicated in their works by Angeli and Hewitt [
4] or Ioannou et al. [
5]. Practical examples of the effectiveness of such activities in relation to crude oil are given by Hassanean et al. [
6], Nesyn et al. [
7], as well as Eshrati [
8]. A reduction of flow resistance of up to 50% forms a feasible option using even very small amounts of surfactants. It is most often a high-molecular polymer, the concentration of which ranges from 20 to 100 ppm. The level of drag reduction caused by the addition of a small amount of an appropriately selected polymer is possible not only in relation to oil liquids with high viscosities. A similar effect can also be obtained in the case of hydrophilic liquids. Moreover, in practice, it is even easier to achieve, since a number of additives applied for this purpose (e.g., polyacrylamide) are more easily distributed in the volume of the slightly viscous water phase than in the oil phase. Surfactants are also used to reduce the drag resistance of a two-phase mixture, including a liquid–liquid system (Edowmonyi-Out [
9]).
However, the application of surfactants with the purpose of lowering the drag resistance of highly viscous oil liquids may have significant limitations. The first of them is faced when even a small content of them is undesirable in the substance processed in a given technology. Complete removal of these additives from the already pumped liquid is practically impossible. The second problem is the flow of those oily substances which contain small volumes of water. In this case, the presence of surfactants promotes the formation of a permanent emulsion. If it is an unplanned and spontaneous phenomenon, its effects may be adverse or even dangerous for the correct operation of a given technological installation. It should also be remembered that the separation of emulsion components is difficult to implement, and its rheological properties may differ significantly from those of its components in a pure state (Krynke et al. [
10]). However, the greatest obstacle is related to the fact that the actual effect of the surfactant cannot be predicted only on the basis of theoretical calculations, and thus at the design stage of the flow system. The selection of the type and amount of surfactant is most often completely based on empirical grounds. Meanwhile, to conduct optimization calculations, it is necessary to have mathematical models (equations) describing the course of a given phenomenon or process. Importantly, such models exist because they describe the results of experimental studies concerning, for example, the resistance of two-phase liquid–liquid flow. One of the few specific phenomena revealed during such flow is the resistance reduction effect.
Any liquid with hydrophobic properties can form the component of the liquid non-permanent two-phase system. However, in technical applications, these are mostly petroleum products or oil substances of various origins. In turn, the hydrophilic liquid is most often just water. Experimental studies concerned with the flow of this type of two-phase liquid–liquid systems carried out on various scales demonstrate the effect of reducing the flow resistance of the highly viscous oil phase can be obtained by introducing a certain amount of water into the pipe, e.g., as described in study Mc Kibben et al. [
11,
12]. Moreover, a decrease in the flow resistance of a highly viscous substance can also be caused by introducing a small amount of a gas phase into the pipe. Such a method is of particular importance when permanent emulsion systems are pumped (in particular, ones classified as O/W type). In their case, the use of water leads to the variations in the volume fraction of the continuous phase and leads to the dilution of the emulsion, and this can adversely affect its functional properties.
The occurrence of the drag reduction effect accompanying two-phase liquid–liquid flow is confirmed by various researchers. In publications of a theoretical nature, the description of the level of this reduction is related to the ratio of the volumes of the phases forming the two-phase system, and thus the variations in the tube surface wetting by each of the liquids and the fluctuations in the distribution of their local velocities. Such an approach is well known because it was presented a long time ago by, among others, Charles and Redberger [
13]. However, in experimental papers, the dominant view is that the drag reduction effect results from changes in two-phase flow structures. These changes lead to phase inversion and thus to a change in the type of liquid–liquid system and its physical properties. Such conclusions are provided by Nädler and Mewes [
14] and Soleimani et al. [
15] among other studies.
The study and description of the phenomena accompanying two-phase liquid–liquid flows still forms a current topic. The study by Ahmed and John [
16] outlines the areas that are related to the scope of the problems that need to be explored and better described. Hence, research is still being carried out with regard to reduction of drag reduction caused by the presence of specific additives (Dosumu et al. [
17]) as well as with the purpose of the better assessment of the flow hydraulics of water–oil systems in straight-axial pipes (Luo et al. [
18]) and process apparatus (Ali et al. [
19]). In addition to completely experimental tests, numerical simulations are also carried out in this area, including studies carried out for two-phase liquid–liquid flow in pipes with large diameter (Rodriguez et al. [
20]) and in microchannels (Kahouadji et al. [
21]).
Regardless of the means applied to explain the reasons responsible for the reduction of drag resistance accompanying two-phase liquid–liquid flow, the authors of the research also propose their own equations that allow to calculate the value of the pressure loss resulting from the flow of a substance in a pipe. Thus, it is possible to use this type of mathematical function in the optimization calculation procedure of flow-through installations. The form of the equations is as comprehensive as can be, and they are supposed to apply to various substances and the conditions of their flow. However, it should be remembered that their scope of applicability is always limited, as these are empirical relationships.
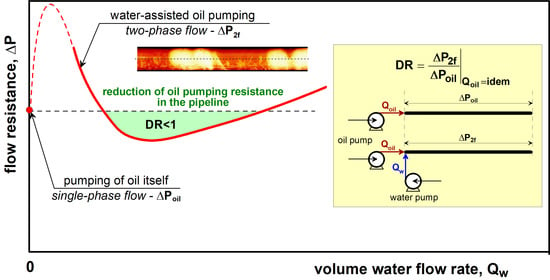
The study reported in this paper contains a proposition of the practical use of one of such equations as a method of predicting drag resistance reduction of a highly viscous oily liquid. The drag resistance effect will result from selection of an adequately controlled flow rate of water fed into the oil flowing in the pipe, i.e., creation of specific conditions for two-phase liquid–liquid flow.
3. Example of Quantitative Assessment of Drag Reduction and Pumping Power
Several series of simulations were performed in order to describe the effects of the practical application of Equation (14). Their aim was to assess the potential energy benefits of accompanying the flow of viscous oil liquids when they are combined with a flux of water.
It is worth recalling that such calculations can be made at the stage of designing the installation or planning its structure modification. At the same time, however, it should be emphasized that the adopted values and the range of the variations in the parameters related to the flow conditions cannot be completely random. First of all, they must correspond to the W/O systems. This can be determined on the basis of the previously mentioned map of flow structures (Hapanowicz et al. [
22]). The appropriate value of
go,s can be derived on the basis of appropriate selection of the diameter of the pipe through which the oil with water needs to be pumped. The determination of a specific diameter of the pipe must be made at the stage of designing or modifying the structure of the installation.
Simultaneously, we need to note that the adopted range of variations in input quantities should correspond to the conditions of applicability of Equation (14). Although its form was developed on the basis of a large set of experimental data, this relation is typically empirical. Under the assumption of the scope of data necessary to conduct simulations, we can notably check whether the limit indicating the possibility of the formation of a permanent emulsion in the pipe will not be exceeded for high flow velocities. The boundaries of emulsion formation are generally indicated by the blue lines shown in
Figure 1, while their location for a specific case can be derived on the basis of the study by Brauner and Ullmann [
28].
In consideration of the above, the simulations adopted the following input data:
oil mass flux: from go,s = 100 to go,s = 600 [kg/(m2·s)];
water mass flux: from gw,s=20 [kg/(m2·s)] to the value that is limited by the results of the simulations;
diameter of flow pipe: d=38 [mm];
densities: for water ρw = 1000 [kg/m3],and oil ρo = 880 [kg/m3];
relative density of highly viscous oil phase in relation to the density of the supplemented water: ρr=ρo/ρw 0.88. This parameter in the liquid–liquid systems is only slightly variable.
viscosities: for water ηw=1 [mPa·s], for oil: ηw=25, 50, 100, 200 and 300 [mPa·s];
relative viscosity of oil in relation to water: ηr= 25, 50, 100, 200, 300.
The results of the calculations offered the possibility of developing series of graphs to illustrate the conditions and the level of drag reduction. However, in the further part of the article, only some of them are presented, as it was sufficient to assess the trend of changes in the course of the described phenomenon and the resulting reduction effect.
Figure 3 illustrates the variations in specific flow resistance of the two-phase mixture ∆
P2f/L recorded for several constant values of mass flux of oil with a viscosity 0.1 [Pa·s]. This value means that oil can be considered as a highly viscous liquid. The variations in the resistances depended on the values of
φw. It is a parameter that is easiest to control in practice and its value, as it results from the relations of liquid feed rates pumped into the pipe. The points on the line have not been marked on the chart on purpose, as the course overlaps exactly with the function (14).
As we can see from
Figure 3, effective changes in the flow resistance of two-phase mixture occur only within a certain range of variations in the water volume ratios. This range is the wider the smaller the flow rate of oil in the pipe. Moreover, it is pointless to exceed a certain value of the water volume ratio (i.e., its flow rate), as it does not lead to a further decrease in the flow resistance of the mixture. It further remains permanent at a certain level. Therefore, it can be concluded that from now on that the decrease in frictional forces (viscosity) resulting from the content of water in non-permanent two-phase system flow can be offset by the increase in its total mass flow rate.
Similar effects can be recorded for systems formed by water and oil with even greater viscosities, which is confirmed by the diagram shown in
Figure 4. It becomes obvious that the flow resistance of such a mixture will be greater compared to the case when the mixture contains oil with a lower viscosity. Clear differences in this respect can be seen by comparing the course of the respective lines in
Figure 3 and
Figure 4.
Similar characteristics in terms of variations in the flow resistance were also obtained in the case of the simulation results gained for systems comprising oil with a different viscosity. This means that the drag reduction effect is also possible in such a case. We can note that the form of the function (14) can be applied to predict the possibility of a decrease in the resistance despite the total increase in the flux of the substance flowing in the pipe. This is also confirmed by the graphs presented in this section.
However, it turns out that the decrease in two-phase flow resistance does not guarantee the drag reduction effect required for pumping the pure oil phase.
Figure 5 contains the simulation results for the
DR index expressed by the Equation (5). The diagram applies to the case of flow of oil with the viscosity
ηr = 100. We can see that the level of drag reduction increases along with an increase in mass flux of oil that is carried in the pipe. It is true that the decreasing characteristics of the changes in the value of index of drag reduction is revealed in the cases of various water volume ratios. However, the increase in its flow rate ultimately leads to the stabilization of the value expressed by
DR. Furthermore, it appears that under certain conditions, despite the phenomenon of drag reduction of the liquid–liquid system, its value still exceeds the flow resistance of the pure oil phase. In
Figure 5, such conditions apply to the part of the line plotted for
go,s = 100 [kg/(m
2·s)], i.e., for the case when the value of
DR is greater than one. We can add that extrapolation of the course of the remaining lines to include a range of small water ratios which can offer similar effects. This fact confirms the very high flow resistance of liquid–liquid systems containing a small amount of water droplets, as noted already earlier in the study.
An increase in oil viscosity leads to the conditions in which it is less probable to gain the value of
DR greater than 1, even for lower mass flux densities of oil, i.e., for its lower flow velocity in the pipe. This is confirmed by the graph contained in
Figure 6, which was developed on the basis of simulations for an oil with a relative viscosity of 300.
In addition, it turns out that as this viscosity increases, the achievable value of
DR becomes even lower (which is considered beneficial). This can be easily confirmed by comparing the course of the lines in
Figure 5 and
Figure 6. There is an obvious conclusion about the beneficial effects of supporting the flow of highly viscous liquids with a water flux, which is well known and presented in the publications of various researchers.
However, the application of this method with regard to any oily liquid does not always prove effective. The graph shown in
Figure 7 was compiled on the basis of the results of calculations performed for oil with a viscosity only 25 times higher than that of water.
As we can see from the arrangement of the lines on the graph, in this case, there is virtually no possibility of obtaining the value DR < 1. The resistance of two-phase flow significantly exceeds the value for pure oil. Nevertheless, the proposed method does not provide the possibility of determining such a range of oil viscosities in which case feeding water into the pipeline would be always unfeasible. Hence, each actual case needs to be assessed separately. However, we should remember that the discussed method of reducing the energy demand for pumping a substance applies to oil liquids of high viscosity. Therefore, their viscosity should be at least one hundred times greater than that of water. In practice, the viscosity of many hydrophobic substances meets this condition, and it is precisely their pressing that consumes energy.
The need to install a water pump also needs to be considered as part of a comprehensive assessment of the possibility of reducing the energy demand for pumping the viscous oil phase. The level of the variations in the total energy resulting from the operation of both pumps can be expressed by the
PR index, which is defined by the expression in (7) and, consequently, one in (10). The values of
PR can be found in
Figure 8, and the presentation contains the simulation results obtained for an oil with a relative viscosity of 25 and confirms that the generation of a two-phase liquid–liquid flow in the pipe can have an effect completely different from one that was projected. The values of
PR for all oil flow rates are greater than one, regardless of the flow rate of water at the inlet to the pipe. However, even with high-viscosity oil, the energies reduction effect becomes very clearly visible. The graphs shown in
Figure 9 and
Figure 10 refer to the results obtained for oil with relative viscosities of 100 and 300, respectively. As we can easily notice, in the case of a more viscous oil, the effect of reducing the pump power will be possible for all considered oil streams.
When we take on an analysis of the course of the lines in
Figure 8,
Figure 9 and
Figure 10, we can easily note that the PR index takes a minimum value before increasing again as
φw is increased further. The relations between parameters marked by
PRmin and
φw gained for oil with various levels of relative viscosity are presented in
Figure 11.
The value of PRmin represents the smallest possible power/energies reduction ratio for the operation of a set of feed pumps. Thus, at the same time, we can state that in the conditions of water flow rate equal to PRmin in the two-phase mixture fed into the pipe, the demand for pumping power will be the lowest. However, this does not mean that at the same time the demand will be smaller from the energy input required for a single-phase flow of pure oil. In order to achieve an effective reduction effect, PRmin value must be lower than 1. If this is not the case, it means that the effect of reducing oil flow resistance cannot be achieved by introducing a much less viscous liquid into the pipe, in this case water.
The analysis of the results of simulations, we can apply a detailed section of the map of two-phase liquid–liquid flow structures (Hapanowicz et al. [
22]). This section is presented in
Figure 12 and three constant oil mass flow rates are marked with blue arrows (as an example).
For these three mass flow rates of oil, simulations were carried out to assess the degree of drag reduction, which also means that we need to assess the power reduction index of the pumping equipment. The colored “stars” represent the conditions corresponding to the lowest power/energy reduction ratio for the given oil flow rate. The presented data refer to an oil with a relative viscosity of ηr = 100, but the simulation results for a different oil mass flux or for an oil with a different viscosity can be presented in a similar way. It should be added that the reduction will also take place outside the conditions indicated by the PRmin but in such a case its level will not be just as considerable.
The analysis of the data in the diagram demonstrates that the value
PRmin decreases with the increase in the flow rate of oil in the pipe. This fact should not come as a surprise, because then the total stream of substances increases. It is important, however, that the values of
PRmin are lower than one, which at the same time means that the effect of reducing energy demand is achievable. Its level will be higher when a water-in-oil dispersion structure is formed in the pipe. Under these conditions, the contact of water with the inner surface of the pipe is more effective compared to the flow of a small number of relatively large water droplets (see flow structures in
Figure 2). It also turns out that the value of the
PRmin index increases (which is adverse) along with the increase in the value of
φ. The reason for this is associated with an increase in the required water stream, and thus a greater demand for energy necessary for its pumping.
On the basis of
Figure 12, we can note the identical value of
gw,s corresponding to
PRmin for all three selected oil mass flux densities. However, this is nothing peculiar. On the basis of the analysis in detail of the form of Equation (14), we can conclude that for a given constant value of
go,s for a given pipe diameter and constant physical properties of both liquids, the value of ∆
P2f is solely the function of the water mass flux. The local extreme of this function corresponds to the lowest flow resistance, and taking into account the form of expressions (7), (9), or (10) also the values of the
PRmin index. However, it is no longer a constant parameter.
In conclusion, it once again appears that the form of Equation (14) forms a prediction of both the decreasing and increasing characteristics of the variations in the resistance of the two-phase liquid–liquid flow. For this reason, it can be applied to conduct simulation and optimization calculations in terms of determining the conditions necessary to reduce the amount of energy necessary for pumping highly viscous oil liquids in the pipe