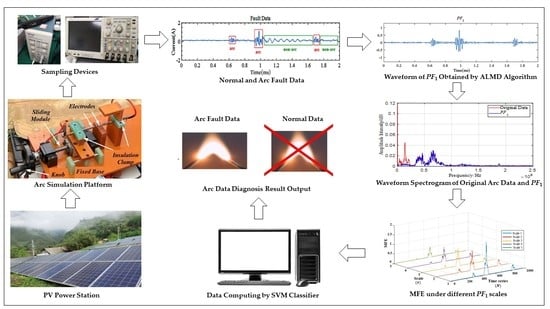
Adaptive Local Mean Decomposition and Multiscale-Fuzzy Entropy-Based Algorithms for the Detection of DC Series Arc Faults in PV Systems

Abstract

DC series arc fault detection is essential for improving the productivity of photovoltaic (PV) stations. The DC series arc fault also poses severe fire hazards to the solar equipment and surrounding building. DC series arc faults must be detected early to provide reliable and safe power delivery while preventing fire hazards. However, it is challenging to detect DC series arc faults using conventional overcurrent and current differential methods because these faults produce only minor current variations. Furthermore, it is hard to define their characteristics for detection due to the randomness of DC arc faults and other arc-like transients. This paper focuses on investigating a novel method to extract arc characteristics for reliably detecting DC series arc faults in PV systems. This methodology first uses an adaptive local mean decomposition (ALMD) algorithm to decompose the current samples into production functions (PFs) representing information from different frequency bands, then selects the PFs that best characterize the arc fault, and then calculates its multiscale fuzzy entropies (MFEs). Eventually, MFE values are inputted to the trained SVM algorithm to identify the series arc fault accurately. Furthermore, the proposed technique is compared to the logistic regression algorithm and naive Bayes algorithm in terms of several metrics assessing algorithms’ validity for detecting arc faults in PV systems. Arc fault data acquired from a PV arc-generating experiment platform are utilized to authenticate the effectiveness and feasibility of the proposed method. The experimental results indicated that the proposed technique could efficiently classify the arc fault data and normal data and detect the DC series arc faults in less than 1 ms with an accuracy rate of 98.75%.

1. Introduction

Recently, demand for clean energy has increased in response to growing environmental concerns and a shortage of fossil fuels. Numerous efforts are being made to replace fossil fuels with renewable energy sources. Renewable energy sources have significant implications for energy consumption in public and private sectors [1,2]. Renewable energy resources (wind, solar, tidal, and geothermal) have emerged as a clean and leading energy source over the last few decades. Solar energy is a prevalent form of green energy—a plentiful, vital, and sustainable energy source. PV systems are gaining popularity due to their accessibility, scalability, environmental friendliness, low cost of fuel, simple architecture, and low carbon footprint [3,4,5]. According to the International Renewable Energy Agency (IRENA), the global photovoltaic industry’s installed capacity has steadily increased since 2011. Rooftop photovoltaic (PV) generation or a solar power farm could be essential in supplying power and supporting various loads [6,7]. With the growth of photovoltaic (PV) energy applications, it is critical to ensure stable and long-term PV energy generation. PV power-generation systems generally operate at a high voltage to maximize the overall efficiency and minimize cable costs; for example, 1500 Vdc technology has been applied on a large scale internationally [8,9,10]. However, high voltage makes it easier for the air to ionize, which increases the likelihood of a DC arc fault. Additionally, the operating environment of photovoltaic power plants is typically harsh. As a result, many cables in photovoltaic (PV) plants are susceptible to arcing due to ruptured insulation. Arcs can generate high-temperature plasma, reducing the efficiency of photovoltaic (PV) energy-generation systems. Arc faults can result in fire or explosions, endangering human safety and property [11,12]. Arc faults are hazardous events that should be detected immediately. Hence, detecting these faults in advance is significant because it can inform the user about the failures of a PV system.

There are two types of DC arc faults in PV power plants: parallel and series arc faults. The parallel arc is a short circuit and occurs when an insulation system suffers a breakdown. The insulation between the two wires can become ineffectual due to cracking, UV degradation, moisture, and animals chewing on them. The parallel arc generates a large amount of current, which can easily be detected by overcurrent protection equipment or insulation monitoring sensors quickly [13,14]. The DC series arc happens when a connection is broken while the PV module produces current. These connections could be soldered joints within the module or the connectors found on wire leads connecting to PV modules. However, due to arc impedance and load impedance, the series arc may only cause a relatively minor change in the current, which is insufficient to melt fuses, and standard overcurrent protection devices are unable to detect the series electric arc. Due to the sustainability of PV DC energies, DC series arcs in PV systems may create explosions and even fire mishaps, posing a hazard to human safety and system reliability [15,16,17]. As a result, an additional reliable detection device for DC series arc fault is critical, especially for the building PV systems. Hence, it is necessary to research the detection of series arc faults.

Numerous approaches have been established in the literature to diagnose series arc faults on the DC side of the PV system, which can be classified into time-domain methods and frequency-domain methods [18,19,20,21,22]. Time-domain methods have high requirements for sampling data. However, DC currents of PV stations are frequently flawed by various interference noises, resulting in nonlinearity and instability in data. It is rather challenging to detect series arc faults by utilizing time-domain methods alone [18]. Hence, frequency-domain methods prevail in the field of series arc fault detection. The frequency-domain analysis algorithms, such as fast Fourier transform (FFT) [19], short-time Fourier transform [20], wavelet transform [21], and empirical mode decomposition [22] have been applied to extract the detection features in the field of DC series arc detection. However, it cannot detect the exact time that the arc occurred when using FFT. The parameters in choosing the window function when using short-time Fourier transform are very strict; if it is too narrow or wide, the detection may deteriorate. The wavelet transform suffers the same problem in selecting the wavelet basis; if an improper wavelet basis function is selected, the ability of wavelet transforms to decompose signals will become bad. The empirical mode decomposition is an adaptive signal decomposition method. By using this method, the original signal can be decomposed into several intrinsic mode functions (IMFs) that characterize the information of different frequency bands. However, there is a general phenomenon of mode mixing between these IMFs. If the mode mixing is severe, it will make the decomposition meaningless.

Artificial intelligent methods such as artificial neural network (ANN) algorithms and other machine learning algorithms are used to detect series arc faults [23,24,25,26,27,28,29,30]. The logistic regression algorithm is utilized to efficiently analyze the experimental results of arc fault in the PV system [25]. Additionally, a distributed PV array fault detection technique based on fine-tuning the naive Bayes model is used to examine the fault condition of the PV array [26]. In [27], a principal component analysis algorithm with blind source separation is presented for timely and reliable identification of series electric arcs in PV systems. The short-observation-window singular value decomposition and reconstruction algorithm offered enhanced proficiency in detecting the series arc faults by applying the coupling method [28]. In [29], a novel approach based on voltage differential protection is utilized to detect series arc faults in low-voltage DC distribution systems. However, the good performance of these methodologies is based on large-scale data training and time-consuming human labeling effort. Nevertheless, it is still a challenge for such methods to be used in a strong noise environment. Among intelligent algorithms, the support vector machine (SVM) algorithm is prominent and has been frequently used to diagnose arc faults based on various information by pioneers [30]. These existing techniques have shown good performance. However, the performance of these techniques highly relies on the extracted detection features. Improperly selected detection features might significantly weaken the detection accuracy. For safety issues, high reliability is needed for fault detection devices. However, these methods exhibit uncertainty in detecting series arc faults, requiring further research.

This research intends to investigate the application of the adaptive local mean decomposition (ALMD) algorithm in extracting the suitable characteristics for DC series arc fault detection in PV systems. The ALMD algorithm is a novel self-adaptive time–frequency analysis method, which is particularly suitable for the processing of multi-component amplitude-modulated and frequency-modulated (AM–FM) signals [31]. When DC series arc faults occur in PV systems, the PV array current signals picked up would exactly display AM–FM characteristics. So, it is possible to diagnose arc faults using ALMD. At present, the ALMD algorithm has been successfully used in electroencephalogram (EEG) signal processing and bearing fault diagnosis [32,33]. The ALMD algorithm is utilized in this research to extract the arc characteristic frequency band components. Based on the decomposition result, the nonlinear dynamic analysis methods can be then easily used to derive the detection features for DC series arc. Among these nonlinear dynamic analysis methods, approximate entropy was often used, which has the advantage of strong noise immunity [34]. However, theoretical analysis and experiments proved that approximate entropy has the problem of self-matching. To tackle this problem, sample entropies with higher computational accuracy and independent data length are proposed [35,36]. Considering that the conventional sample entropy can only depict signal features from a single scale, Costa proposed a fuzzy entropy that can characterize multiscale complexity based on the sample entropy [37]. This paper utilizes multiscale fuzzy entropies (MFEs) as the feature to better analyze the signal characteristics. After a comprehensive investigation, this paper proposes an advanced arc detection algorithm combining ALMD, MFE, and SVM to detect DC series arc faults in PV systems. The proposed technique is also compared to the logistic regression algorithm and naive Bayes algorithm in terms of several metrics assessing algorithms’ validity for detecting arc faults in PV systems. Furthermore, the effectiveness of the proposed combination method in detecting DC series arc faults is verified through experiments, with an accuracy of 98.75%.

The primary contribution of this paper lies in the arc feature extraction method by combining the ALMD algorithm and the multiscale fuzzy entropy (MFE), which consequently makes the following SVM classifier perform better in DC series arc fault identification. The benefit of SVM is obvious. As established by [30], SVM is a standard binary classifier with specific advantages for handling issues involving high-dimensional pattern recognition, short sample sizes, and nonlinearity. To our knowledge, this is the first time the ALMD algorithm has been applied in DC series arc fault detection. The features of the proposed method include:

• The use of the ALMD algorithm to obtain the concerned components that best depict the arc characteristic frequency band information from the raw signal, which effectively eliminate the influences of the complex environment noise.
• The choice of the multiscale fuzzy entropy (MFE) of the concerned component as the arc detection feature, which makes the following SVM classifier algorithm perform extraordinarily well in complex nonlinear circumstances with complicated background noise.

The rest of this paper is organized as follows. In Section 2, the arc fault detection algorithm based on ALMD and MFE is proposed. Then, the effect of the proposed DC series arc fault detection algorithm is presented in Section 3. Eventually, Section 4 includes the conclusion of this paper.

2. Algorithm for Detecting Arc Faults

2.1. Characteristics of Arc Fault Data Acquisition

The proposed series arc fault diagnostic approach was applied on the PV power plant, at Songjialiangzi village, Hubei province, China. The front and side view of the PV power plant is shown in Figure 1. To investigate the characteristics of a series arc fault, a PV arc-fault experimental platform structure was created and presented in Figure 2.

The experimental platform consists of a PV array, a breaker, a resistor load, an arc generator, and current sampling equipment. The arc generator is designed in accordance with the UL 1699B standard, and its structure is shown in Figure 3. The sampling frequency is kept at 500 kHz. The sampling rate was tried out through experiments combining the characteristic arc frequency band and the proposed method. The complete module of the arc generator is shown in Figure 4, while the burning arc is captured in Figure 5. Furthermore, the sampling devices such as the oscilloscope (Tektronix DPO 4104B-L) and current probe (Tektronix TCPA300+TCP312A) are utilized in experimental work. In the field, the utilization of the high-frequency current transformer coil and sampling resistor is recommended.

In the experiments, the two electrodes are tightly contacted initially. To induce arcs, the two electrodes are separated to create a gap by rotating the sliding module. Then, the current signal is collected using the acquisition devices (the current probe and the oscilloscope). By removing the arc generator, normal current data can be obtained. The data under different load conditions are obtained by changing the load resistance value. The waveforms of the collected normal current data and the arc fault current data are shown in Figure 6. It can be seen that the waveform of the normal data is relatively smoother, and the waveform of the arc fault data has prominent oscillations.

Figure 7 illustrates the frequency-domain information of normal current and fault current data after a Fourier transform. The information in the 0–100 kHz frequency band (the DC series arc fault characteristic frequency band) differentiates fault data from normal data. For satisfactory results, the authors strongly suggest that the minimum sampling rate and accuracy should be not less than 80 kHz and 5%, respectively. The lower the sampling rate, the lower the detection accuracy for weak and transient arcs. With an 80 kHz sampling rate, the effective signal frequency range is less than 40 kHz and the detection accuracy dropped to less than 92% in our experiments.

2.2. Adaptive Local Mean Decomposition (ALMD) Algorithm

The ALMD algorithm, introduced by Jonathan S. Smith in 2005, is a signal decomposition approach that adaptively decomposes a complex signal into a set of production functions (PFs) [31]. A PF component is obtained by multiplying an envelope signal with a pure frequency modulation (FM) signal. The ALMD algorithm maintains the amplitude and frequency characteristics of the original signal, and the combination of the instantaneous amplitude and instantaneous frequency of all PF components gives the whole time-frequency distribution of the original signal. The decomposition process for an original signal is as follows:

(i)

Find all local extreme points of the original signal x(t), including all maximal and minimal points. Then calculate the i_th mean $m_i$ of each two adjacent extrema $n_i$ and $n_{i+1}$ by Equation (1).

$$m_i=\frac{n_i{+n}_{i+1}}{2}$$

(1)

Connect all mean values $m_i$ by straight lines. Then use the moving averaging method to form a smoothly varying continuous local mean function $m_{11}\left(t\right)$. In this article, the moving averaging algorithm is applied by Equation (2). The detailed steps of the moving averaging algorithm can be found in literature [32].

$$m_{11}\left(t\right)=\frac{1}{3}\left(m_{i-1}+m_i+m_{i+1}\right)$$

(2)

(ii)

The corresponding local magnitude of each half-wave oscillation is calculated by Equation (3).

$$a_i=\frac{\left|n_i-n_{i+1}\right|}{2}$$

(3)

Similarly, connect all the envelope estimates with straight lines. The smoothly varying continuous envelope function a₁₁(t) is obtained by the same smoothing process in step (i).

(iii)

Separate the local mean function $m_{11}\left(t\right)$from the original signal $x\left(t\right)$ using Equation (4).

$$h_{11}\left(t\right)=x\left(t\right)-m_{11}\left(t\right)$$

(4)

(iv)

Then, demodulate $h_{11}\left(t\right)$ by dividing it by $a_{11}\left(t\right)$, as presented in Equation (5).

$$s_{11}\left(t\right)=\frac{h_{11}\left(t\right)}{a_{11}\left(t\right)}$$

(5)

Apply the procedures of step (i) and step (ii) on $s_{11}\left(t\right)$, then the envelope function $a_{12}\left(t\right)$ of $s_{11}\left(t\right)$ can be calculated according to step (iii) and step (iv). If $a_{12}\left(t\right)$ is not equal to 1, it means that $s_{11}\left(t\right)$ is not a pure FM function and the above steps need to be repeated by $n$ iterations until $a_{1\left(n+1\right)}$ is equal to 1—this means that $s_{1n}\left(t\right)$ is a pure FM function. The formula is repeated $n$ times as shown in Equation (6):

$$\begin{array}{c}{h}_{11}\left(t\right)=x\left(t\right)-m_{11}\left(t\right)\\ h_{12}{\left(t\right)=s}_{11}\left(t\right)-m_{12}\left(t\right)\\ ⋮\\ h_{1n}{\left(t\right)=s}_{1(n-1)}\left(t\right)-m_{1n}\left(t\right)\end{array}\}$$

(6)

where:

$$\begin{array}{c}{s}_{11}\left(t\right)=\raisebox{1ex}{$h_{11}\left(t\right)$}\!\left/ \!\raisebox{-1ex}{$a_{11}\left(t\right)$}\right.\\ s_{12}\left(t\right)=\raisebox{1ex}{$h_{12}\left(t\right)$}\!\left/ \!\raisebox{-1ex}{$a_{12}\left(t\right)$}\right.\\ ⋮\\ s_{1n}\left(t\right)=\raisebox{1ex}{$h_{1n}\left(t\right)$}\!\left/ \!\raisebox{-1ex}{$a_{1n}\left(t\right)$}\right.\end{array}\}$$

(7)

The condition for stopping the iteration is shown in Equation (8).

$$\underset{n\to \infty }{\lim }{a}_{1n}\left(t\right)=1$$

(8)

In practice, to reduce the number of iterations and the calculation time, Equation (9) can be used instead of Equation (8) as the termination condition of the iteration without affecting the decomposition effect.

$$a_{1n}\approx 1$$

(9)

(v)

The envelope signal $a_1\left(t\right)$ is obtained by multiplying all the envelope estimation functions $a_{1i}\left(t\right) \left(i=1,2,\dots ,n\right)$ generated during the iterative process according to Equation (10).

$$a_1{\left(t\right)=a}_{11}{\left(t\right)a}_{12}\left(t\right)\cdots a_{1n}\left(t\right)={{\displaystyle \prod }}_{q=1}^n{a}_{1q}\left(t\right)$$

(10)

(vi)

The first production function ${\mathit{PF}}_1\left(t\right)$ of the original signal is obtained by multiplying the resulting envelope signal $a_1\left(t\right)$ with the pure FM signal based on Equation (11).

$${\mathit{PF}}_1{\left(t\right)=a}_1{\left(t\right)s}_{1n}\left(t\right)$$

(11)

(vii)

The first PF component $P{F}_1$ is separated from the original signal $x\left(t\right)$, then a new signal $u_1\left(t\right)$ is obtained. Repeat the above steps with $u_1\left(t\right)$ as the original data. Iterate P times until $u_P\left(t\right)$ is a monotone function according to Equation (12):

$$\begin{array}{c}{u}_1\left(t\right)=x\left(t\right)-{\mathit{PF}}_1\left(t\right)\\ u_2{\left(t\right)=u}_1\left(t\right)-{\mathit{PF}}_2\left(t\right)\\ ⋮\\ u_{\mathrm{P}}{\left(t\right)=u}_{\mathrm{P}-1}\left(t\right)-{\mathit{PF}}_{\mathrm{P}}\left(t\right)\end{array}\}$$

(12)

(viii)

As mentioned above, several PFs can be obtained using the ALMD algorithm, and then the most suitable PF needs to be selected. Since kurtosis can effectively characterize the vibration amplitude, the PF with the largest kurtosis value is selected as the optimum PF, which includes more information about the arc fault. The kurtosis value of each PF is calculated according to Equation (13), and the normalized kurtosis value (NKV) of each PF is calculated by Equation (14).

$$K_p=\frac{1}{H}{{\displaystyle \sum }}_{h=1}^H{\left(P{F}_{ph}\right)}^4$$

(13)

$$U_p=\frac{K_p}{{{\displaystyle \sum }}_{p=1}^P{K}_p}$$

(14)

where $K_p$ represents the kurtosis value of the $p$-th PF, H is the length of the original data x(t), which is also the length of the PFs. The $U_p$ is the normalized kurtosis value (NKV) of the$p$-th PF, and P is the number of PF.

2.3. Multiscale Fuzzy Entropy (MFE)

The multiscale fuzzy entropy (MFE) algorithm is used to measure the complexity of time series signals at different scales. It can be calculated by the following steps.

(i)

First, a segment of data samples in the initial time series signal are chosen using a sliding window of fixed length. Then, the selected sequence of data samples {u(i): 1 ≤ i ≤ N} within the sliding time window has to be coarsened. The coarsened sequence at $\tau$ scale is created by Equation (15).

$$y_{\tau }\left(j\right)=\frac{1}{\tau }{{\displaystyle \sum }}_{i=j}^{j+\tau -1}u\left(i\right), 1\le j\le N-\tau +1$$

(15)

In Equation (15), $\tau$ represents the scale factor used for coarse granulation. When $\tau =1$, the new time series is the same with the original time series.

(ii)

Secondly, the coarsened sequence is transformed into a set of vectors$\{X_j^m:1\le j\le \left(N-\tau -m+2\right)\}$, which is represented as in Equation (16):

$$X_j^m=\left\{y_{\tau }\left(j\right), y_{\tau }\left(j+1\right),\cdots ,y_{\tau }\left(j+m-1\right)\right\}-\overline{y_{\tau }\left(j\right)}, 1\le j\le N-m-\tau +2$$

(16)

In Equation (16), m is the length of the newly constructed vectors. $\overline{y_{\tau }\left(j\right)}$ can be calculated by Equation (17):

$$\overline{y_{\tau }\left(j\right)}=\frac{1}{m}{{\displaystyle \sum }}_{k=0}^{m-1}{y}_{\tau }\left(j+k\right)$$

(17)

Then, define the maximum distance between $X_i^m$ and $X_j^m$ as $d_{ij}^m$:

$$d_{ij}^m=d\left[X_i^m,X_j^m\right]=\underset{k \in \left(0,m-1\right) }{\max }\left|\left(y_{\tau }\left(i+k\right)-\overline{y_{\tau }\left(i\right)}\right)-\left(y_{\tau }\left(j+k\right)-\overline{y_{\tau }\left(j\right)}\right)\right|$$

(18)

Next, the similarity degree $D_{ij}^m$ of vectors $X_j^m$ and $X_i^m$ is defined by fuzzy function $\mu \left(d_{ij}^m,\beta ,\mathrm{r}\right)$, as shown in Equation (19).

$$D_{ij}^m=\mu \left(d_{ij}^m,\beta ,r\right)=\{\begin{array}{c}1, 0\le d_{ij}^m\le r\\ {\mathrm{e}}^{-[\mathit{ln}\left(2\right)]\ast {\left(\frac{d_{ij}^m-r}{r}\right)}^{\beta }}, d_{ij}^m>r\end{array}$$

(19)

where $\beta$ is the width of the fuzzy function boundary; r is the boundary gradient of the fuzzy function boundary.

(iii)

Finally, the multiscale fuzzy entropy at $\tau$ scale of the time series {u(i):1 ≤ i ≤ N} can be calculated as:

$$FuzzyEn\left(m,\beta ,r\right)=\mathit{ln}\left[{\varphi }^m\left(\beta ,r\right)\right]-\mathit{ln}[{\varphi }^{m+1}\left(\beta ,r\right)]$$

(20)

where:

$${\varphi }^m\left(\beta ,r\right)=\frac{1}{N-m}{{\displaystyle \sum }}_{i=1}^{N-m}(\frac{1}{N-m-1}{{\displaystyle \sum }}_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{N-m}{D}_{ij}^m)$$

(21)

And ${\varphi }^{m+1}\left(\beta ,r\right)$is calculated using the same method as ${\varphi }^m\left(\beta ,r\right)$. By calculating MFE through the above steps, the complexity of the time series signal at different scales can be characterized.

2.4. Arc Fault Detection Algorithm Execution Steps

In this paper, the adaptive local mode decomposition (ALMD) algorithm and multiscale fuzzy entropy (MFE) are combined to form a new arc characteristic quantity-detection algorithm to address the complicated background interference noises in the field of the PV system. The specific steps for executing the proposed algorithm are explained below, and the block diagram is illustrated in Figure 8.

(i)

The collected current data is decomposed using the ALMD algorithm to obtain multiple production functions (PFs) in the first step.

(ii)

In the second step, the normalized kurtosis value (NKV) of each production function (PF) is calculated, and the PF with the largest NKV is selected as the PF to be analyzed further.

(iii)

In the third step, the MFE values of the selected PF are calculated. Firstly, the length N of the sliding window for calculating the multiscale fuzzy entropy (MFE), the scale factor τ, the newly-constructed vector size m, the values of β and r are initialized. Then N samples are selected from the selected production functions by using the sliding window. The selected samples {u(i):1 ≤ i ≤ N} are coarsened using Equation (15). Then the coarsened sequence {y_τ (j):1 ≤ j ≤ (N − τ + 1)} is converted into vectors by using Equations (16) and (17). Finally, by defining the distance and similarity functions of these vectors {X_l^m:1 ≤ l ≤ (N − τ − m + 2)}, the MFE of the selected PF data within the sliding time window can be calculated using Equations (18)–(21). Then slide the data window forward, calculate the MFE of the selected PF data within the new sliding time window again. Until all the MFE values of the selected PF are derived window by window.

(iv)

In the final step, whether arc fault occurs is classified by using a support vector machine (SVM) algorithm. The SVM algorithm used in this paper is the LibSVM program provided by Chih-Chung Chang and Chih-Jen Lin, which will not be iterated in this paper [38].

3. Validation of the Proposed DC Series Arc Fault Detection Method

3.1. Selection of the Suitable Production Function (PF) after the ALMD Algorithm

The ALMD algorithm decomposes the original sampled data, which are sampled at a rate of 500 kHz. The waveforms of different production functions (PFs) extracted are shown in Figure 9. It can be seen that PF₁~PF₅ covers various frequency bands without aliasing, and PF₁ contains more arc characteristic frequency band information in the original signal. Fourier transform is performed on the randomly selected original arc data and its decomposed PF₁ signal. The frequency-domain information of the original arc data and its decomposed PF₁ is shown in Figure 10. It can be seen that PF₁ does contain the relevant information in the concerned frequency band and are equivalent to the excellent high-pass filtered result of the original series arc current. Furthermore, when the current changes occur dramatically due to an arc fault, PF₁ will fluctuate synchronously, as shown in Figure 9. Consequently, PF₁ was selected in this method as the most suitable PF associated with the DC series arc fault detection.

The normalized kurtosis value (NKV) of each of the decomposed PFs are calculated and the results are shown in

Table 1. Normalized kurtosis values (NKVs).

Variable	PF1	PF2	PF3	PF4	PF5
NKV	0.95613	0.04343	0.00030	0.00009	0.00005

. According to the previous section, the larger the NKV of a PF, the more signal information it contains. The method of calculating the NKV of the decomposed PFs is more convenient than the method of directly observing information in the time or frequency domain.

In order to authenticate whether PF₁ contains more arc characteristic information and is the most suitable PF in other cases, the ALMD algorithm is performed on three sets of normal and faulty data, respectively, which are selected randomly. The NKV of each decomposed PF is calculated. The results are shown in

Table 2. NKVs of different PFs obtained by decomposing sets of normal and arc data.

NKV	Label	PF1	PF2	PF3	PF4	PF5
Normal	1	0.93467	0.06062	0.00439	0.00021	0.00011
Normal	2	0.97315	0.02642	0.00020	0.00015	0.00008
Normal	3	0.90612	0.08131	0.01240	0.00016	0.00001
Fault	1	0.97959	0.02001	0.00021	0.00011	0.00009
Fault	2	0.97971	0.01855	0.00170	0.00003	0.00003
Fault	3	0.91612	0.08339	0.00025	0.00017	0.00006

. It can be seen that PF₁ decomposed from different signals has the largest NKV in our case, which verifies that PF₁ contains more feature information about the DC series electric arc and is the most suitable PF.

3.2. Calculation of Multiscale Fuzzy Entropy (MFE)

The value of multiscale fuzzy entropy (MFE) is calculated from PF₁. The length N of the sliding window is set to 50 in this study. A too-large value of N will occupy more computing resources and meanwhile will weaken the timeliness of the proposed method. However, a too-small value of N will weaken the detection accuracy. The experimental results show that the result is good with 40 to around 60 samples at a 500 kHz sampling rate. Therefore, the sliding window of 50 is chosen in this study. The scale factor τ is chosen as 5. For the parameters of the similarity function $D_{ij}$, $m$ and $\beta$ are chosen as 3 and 2 respectively. The$r$ is calculated by utilizing Equation (22), where S is the standard deviation of the initial data of the selected production function (PF).

$$r=0.15\ast r$$

(22)

The waveforms of the calculated MFE of the original 1000 data and their PF₁ under different scales are shown in Figure 11. A scale of 1 means the initial data. For comparison convenience, the time-domain waveforms of the original sampled data and its decomposed PF₁ are plotted in Figure 12. The parts circled in red in Figure 12 are the moments when the effects of arc are more prominent. It can be easily observed from Figure 11 and Figure 12 that the MFE successfully meets the requirement to characterize arc fault information. Once the arc fault occurs, there is a significant change in the MFE, and its magnitude is proportional to the severity of the arc.

3.3. Validation of the Proposed DC Series Arc Fault Detection Algorithm

In order to validate the authenticity of the proposed DC series arc detection algorithm, 24 sets of current data were obtained from the experimental platform mentioned in Section 2.1. Twenty-four experiments were carried out at different load resistances, including 12 under the normal condition and 12 under the series arc fault. There were 1000 data samples in each data set at the 500 kHz sampling rate. The ALMD algorithm is executed on the collected current data set. When calculating MFE of the selected production function (PF), the window width was set to 50, and the window shift is set to 1. The MFE was calculated for each data window until all the data of the selected PF are windowed. Consequently, 951 MFE data was obtained for each data set.

In order to train and validate the support vector machine (SVM) algorithm effectively, 3200 MFE data were manually selected out from these 24 sets of 951 MFE data. A set of 2400 MFE data, which were randomly selected from the 3200 MFE data, were used for training the SVM algorithm. The remaining 800 MFE data were used for testing. The training and testing data cover both arc fault conditions and normal conditions.

The SVM program used in this paper is the LibSVM program provided by Chih-Chung Chang and Chih-Jen Lin [38]. The radial basis function (RBF) is presented as the kernel function of the SVM, and the particle swarm optimization (PSO) algorithm is used to select the optimal penalty parameter c and kernel function parameter g for the SVM.

Table 3. Testing results.

Result Type	TP	FP	TN	FN	Total
Number	260	0	530	10	800
Percentage	32.5%	0%	66.25%	1.25%	100%

presents the test result of the proposed method on the 800 testing data, in which TP, FP, TN, and FN are four types of detection results.

• TP (true positive): The number of arc fault data that are classified as representing an arc fault condition.
• TN (true negative): The number of normal data that are classified as representing a normal condition.
• FP (false positive): The number of normal data that are classified as representing an arc fault condition.
• FN (false negative): The number of arc fault data that are classified as representing a normal condition.

The TP and TN represent cases of accurate detection, whereas the FP and FN represent examples of the wrong detection. From Table 3, it can be seen that 790 of the 800 samples are correctly identified with an accuracy of 98.75%. The evaluation metrics in

Table 4. Comparison of different metrics measuring the validity of the proposed DC series arc fault detection algorithm with other algorithms.

Different Algorithms	Metrics
	Accuracy	Misclassification	Precision	Specificity	Sensitivity (Recall)
Logistic regression	93%	7%	100%	100%	82.8%
Naive Bayes	97.75%	2.25%	96.54%	98.33%	96.54%
The proposed method	98.75%	1.25%	100%	100%	96.30%

are defined as following:

• Accuracy (total correct outcomes/total outcomes) = (TP + TN)/(TP + TN + FP + FN).
• Precision (true positive outcomes/predicted positive outcomes) = (TP)/(TP + FP).
• Misclassification (total incorrect outcomes/total outcomes) = (FP + FN)/(TP + TN + FP + FN).
• Specificity (true negative outcomes/total actual negative outcomes) = (TN)/(TN + FP).
• Sensitivity (recall) (true positive outcomes/total actual positive outcomes) = (TP)/(TP + FN).

Table 4 presents the comparison of the proposed algorithm with other algorithms (logistic regression [25] and naive Bayes [26]) in terms of different metrics measuring the validity of the specified algorithm in detecting DC series arcs in the PV system. The logistic-regression-based arc detection method achieves an efficiency of 93%, while the naive-Bayes-based arc diagnosis algorithm attains an accuracy of 97.75%. It can be observed that the proposed DC series arc detection method performs well, with an accuracy rate of 98.75%, 100% precision, 1.25% misclassification, 100% specificity, and 96.30% recall. Only 10 out of 800 samples were incorrectly identified. The evidence presented here supports the notion that the suggested algorithm is sufficiently robust to detect DC series arc faults effectively. The arc detection time for the proposed method is less than 1 ms, whereas the DC series arc fault is detected within 15 ms by utilizing an approach based on voltage differential protection [29]. However, the authors would like to point out that high-level wide-band noise might dim the performance of the method suggested in this study. It is highly suggested that noise-band analysis and arc characteristic frequency band analysis should be conducted before applying the proposed method. Meanwhile, the sampling rate should be designed according to the concerned arc characteristic frequency band. Correspondingly, the scale factor τ should be also carefully designed to get a balance between the calculating complex and capability of detecting transient arcs at an early stage.

4. Conclusions

This paper proposes a novel fault detection method for DC series arcs based on the combination of adaptive local mean decomposition (ALMD), multiscale fuzzy entropy (MFE), and support vector machine (SVM) algorithms for PV systems. In the arc feature derivation process, the data is first decomposed into several production functions (PFs) using the ALMD algorithm. Then the PF most strongly related to the arc fault characteristics is selected to calculate the MFEs, which are used as the arc detection features. The derived MFE values are inputted to the SVM, and the trained SVMs were used to identify arc faults. Arc fault data acquired from a PV arc-generating experiment platform were utilized to authenticate the effectiveness and feasibility of the proposed method with a 98.75% accuracy rate. A DC series arc fault was detected within 1 ms by utilizing this proposed methodology. The main advantages of the proposed arc fault detection methodology include that the ALMD algorithm performs better in protruding the arc characteristic in this methodology, effectively eliminating the influences of the complex environment noise and making the subsequent classification algorithm easier. The MFE successfully converts the selected production function (PF) vibration into an amplitude change of an arc detection characteristic, making it straightforward to use the SVM algorithm. The suggested methodology’s computational time and fault detection speed can be enhanced by decreasing the sliding window. However, the relevance of the results may suffer at the same time. Users can maintain a suitable balance between them based on the requirements of the specific application under consideration.