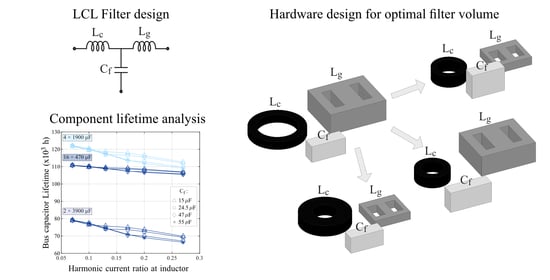
LCL Filter Parameter and Hardware Design Methodology for Minimum Volume Considering Capacitor Lifetimes

Abstract

A design methodology for minimum volume of LCL filters applied to grid connected converters is proposed. It combines the determination of filter parameter values (inductances and capacitances) to hardware design (component technology and inductor construction). Using the proposed strategy, different combinations of L-C-L that meet standard restrictions are determined. The influence of the harmonic content that results from filter design is considered in order to estimate component losses, and filter and bus capacitor lifetimes. Results are presented for filters that lead to the smallest volume, highest capacitor lifetime, or a compromise between both. A case study with three different magnetic material technologies and two types of capacitors is done. The design methodology is experimentally validated for a 1 kW converter. Step-by-step procedures for the determination of filter parameters and inductor hardware design are provided.

1. Introduction

Be it for renewable energy generation or uninterruptible power sources, the use of pulse-width modulated power converters enables the synthesis of voltages with low harmonic distortion. These converters operate at switching frequencies well above the fundamental of $50/60$ Hz [1,2]. Switching produces high frequency harmonics that must be attenuated to avoid disturbances to other loads connected to the grid. Therefore, there are specific standards that determine the harmonic injection limits [3,4,5].

The use of passive filters is common for the mitigation of harmonic currents at switching frequency, well above the control system active range. However, due to their low attenuation rate, purely inductive filters (L) may result in large and heavy components, because a high inductive reactance is needed; which also leads to a high voltage drop [6]. For these motives, the use of LCL filters becomes attractive due to their reduced component dimensions. The main disadvantage associated to LCL filters is the instability caused by the resonance of filter elements, demanding some sort of damping [7,8,9,10].

The definition of the electrical parameters of the LCL inductance and capacitance is not a trivial task. Based on a limit of harmonic injection determined by the standard, the LCL filter design methodologies are diverse [1,2,6,7,8,9,11,12,13,14,15]. The most common strategy consists of setting a fixed value for the filter capacitance ($C_f$), usually chosen as a value equal to or below 5% of the base capacitance ($C_b$), and to design the converter ($L_c$) and grid ($L_g$) side inductors with a ratio “r” between them. This ratio is sometimes adjusted to achieve a desired filter performance [8,11,16].

A slightly different approach is to set $C_f\le 0.05C_b$ and determine $L_c$ for a desired current ripple ($\Delta$I) at the converter input, calculating $L_g$ using the ratio “r” [6,7,9,14]. Similarly, it is also possible to design $L_c$ to obtain a certain harmonic current amplitude at the switching frequency [12]. Other methodologies of designing LCL filters may include modeling the system using the extended harmonic domain [2], using filter transfer functions [6,13], or employing genetic algorithms [17].

With respect to the component design, a discussion on the relation of losses to the inductance value, including damping losses, was done by [1], where it was shown that there is a minimum value for the inductance of the LCL filter to minimize losses. Another work [18], seeks to optimize the relationship between losses and volume, taking into consideration the temperature of the magnetic materials. However, neither authors have evaluated the impact of the technologies they used on the losses and volume, which are decisive to the design. In [16] the use of different magnetic material technologies for the LCL filter is studied, but not from a design methodology perspective. In [19] a design methodology for the LCL filter including EMI consideration is presented; nanocrystalline cores are chosen among four materials, but no comparative analysis among component designs is included.

In the aforementioned works that analyzed the LCL filter considering component design, none have considered the influence of the filter design on the capacitors, despite the fact that the current ripple on the converter side influences the losses and lifetime of the filter and DC bus capacitors ($C_{bus}$) [20]. On the other hand, works that discuss capacitor lifetime do not do it in conjunction with the parametric and hardware design of the filter. These works aim to evaluate the capacitor lifetime using mission profiles [20,21], or seek optimization of volume, cost, reliability, and losses, making use of linearized models of the physical characteristics of the capacitors [22].

This way, the literature on the subject lacks design methodologies that propose to optimize the parametric LCL filter design (values of L and C) in light of losses, volume and capacitor lifetime; discussing the advantages and disadvantages from decisions in the parametric design; considering the impact on the hardware and addressing the used technologies.

A common objective for optimization is cost [23,24,25,26], for competitive market reasons. However, component cost has periodical and local variations, involving non-deterministic variables that depend of technological development, competition among manufacturers, geopolitical factors, availability, and market segment. This way, the obtained results in a cost optimization may be localized, and not applicable to other situations. On the other hand, volume and loss optimization can be more useful, and employed in different situations, permitting an ideal compromise among design variables.

With this in mind, this work employs a design methodology based on the sweeping of $C_f$ values, and of the amplitude of the switching frequency harmonic current in $L_c$ (converter-side). Based on the specifications of the converter and normative restrictions, numerous combinations of L-C-L are found by sweeping. The discretion of possible solutions is made by analyzing the hardware design of each component, considering the use of different technologies, present on a database. With the converter waveforms, losses and temperature in each component are estimated, as well as the lifetimes of capacitors $C_f$ and $C_{bus}$. With this, the objective is to, while meeting normative restrictions, minimize filter volume, maximize capacitor lifetimes, or find a suitable compromise between both. The design methodology is summarized in Figure 1.

The parametric design is validated by waveform measurement, demonstrating compliance to the adopted standard. The hardware design is validated by loss measurement, since it is dependent on their adequate estimation.

2. Filter Parametric Design

As a case study, the input stage of a double-conversion uninterruptible power source (UPS) will be analyzed, as illustrated in Figure 2. This UPS topology consists of two converters connected back-to-back: a rectifier in the input stage, which regulates DC bus voltage and corrects power factor; and an inverter on the output stage, which provides a sinusoidal voltage to the load [27].

As mentioned, the LCL filter is designed to meet the restrictions of injected harmonics into the grid. In this work, the IEC 61000-3-4 standard [5] is considered. The LCL filter is designed per-phase, since this topology allows the converter to be split into three single-phase half-bridge converters. The L-C-L values are determined using the transfer function of the filter.

In order to find an optimal design considering losses, volume and capacitor lifetimes, the developed methodology performs a sweep of filter capacitance ($C_f$) values and of harmonic current amplitudes ($I_{c,f_s}$) on the converter-side inductor ($L_c$). The purpose of this sweep is to explore the filter design possibilities considering normative limits, while not being restricted to a predetermined value of current ripple and/or filter capacitance. The reduction of filter volume is evaluated in light of a possible compromise with capacitor lifetimes.

The developed methodology does not consider the presence of grid inductance nor of an input transformer, since these are typically unknowns. Therefore, the filter is designed for a grid without any inductive characteristic, meeting by itself the restrictions determined by the adopted standard. Otherwise, the grid and transformer leakage inductances would add to the grid-side inductor ($L_g$).

2.1. Converter-Side Inductor

With a phase-shifted PWM modulation, the expression for the converter-side voltage ($v_c$) comprises its DC and fundamental components, as well as its switching harmonics and side lobes. The LCL filter is designed to attenuate the highest amplitude harmonic generated by the converter, which occurs at the switching frequency ($f_s$):

$$V_{c,f_s}=\frac{2V_{DC}sin\left(\frac{\pi }{2}\right)}{\pi }{J}_0\left(\frac{\pi }{2}{m}_a\right)$$

(1)

at which $V_{DC}$ is the bus voltage, $m_a$ the modulation index, and $J_0$ a zero order Bessel function. Disregarding voltage drops on the inductors, $m_a$ can be determined by:

$$m_a=\frac{V_{g}2\sqrt{2}}{V_{DC}}$$

(2)

where $V_g$ is the grid voltage (RMS value).

Assuming a Thévenin equivalent circuit in which $L_g$ and $C_f$ are part of the grid impedance, the value of $L_c$ can be determined using the transfer function of an L filter:

$$\frac{I_c\left(s\right)}{V_c\left(s\right)}=\frac{1}{s{L}_c}$$

(3)

where $V_c\left(s\right)$ is replaced by $V_{c,f_s}$ from (1), and $I_c\left(s\right)$ is replaced by the amplitude of the current harmonic of $L_c$ at the switching frequency ($I_{c,f_s}$), which is varied by the sweep.

2.2. Grid-Side Inductor

The grid-side inductor is designed to attenuate the remaining harmonics that are not filtered by $L_c$ and $C_f$. The transfer function of the LCL filter with passive damping is used:

$$\frac{I_g\left(s\right)}{V_c\left(s\right)}=\frac{C_f{R}_{f}s+1}{L_c{L}_g{C}_f{s}^3+\left(L_c+L_g\right)C_f{R}_f{s}^2+\left(L_c+L_g\right)s}$$

(4)

at which $R_f$ is the value of the damping resistor, $V_c\left(s\right)$ once more is replaced by $V_{c,f_s}$, and $I_g\left(s\right)$ is replaced by its highest harmonic amplitude ($I_{g,f_s}$).

The value of $I_{g,f_s}$ is determined using the limit of admissible harmonic current, set by the standard. It is specified in terms of the ratio between the amplitudes of the switching frequency to the low frequency current: $I_{g,f_s}/I_{g,lf}$. For IEC 61000-3-4, $I_{g,f_s}/I_{g,lf}$ must be ≤0.6%.

The dependence of $L_g$ with regards to $C_f$, $L_c$ and $R_f$ is shown in (4). $R_f$ is related to the resonant frequency ($f_{res}$), which must be between 10 times the low frequency and 0.5 times the switching frequency [6,7]:

$$\begin{array}{c}\hfill f_{res}=\frac{1}{2\pi }\sqrt{\frac{L_c+L_g}{L_c{L}_g{C}_f}}\end{array}$$

(5)

$$\begin{array}{c}\hfill R_f=\frac{1}{3\left(2\pi f_{res}{C}_f\right)}.\end{array}$$

(6)

Since $R_f$ and $L_g$ are both unknowns, the procedure of obtaining the value of $L_g$ is iterative. As a starting point, $f_{res}=f_s/2$ can be assumed. $R_f$ is calculated by (6) and used in (4) to estimate $L_g$. Then, $f_{res}$ and $R_f$ are re-calculated, and (4) is used once more. With the second estimate of $L_g$, $f_{res}$ and $R_f$ are adjusted with (5) and (6). This procedure reduces the need for iterations of $L_g$ and $f_{res}$, that must be repeated until the desired attenuation of $I_{g,f_s}/I_{g,lf}$ is obtained.

The main drawback of LCL filters is its instability, caused by the resonance of its elements. Several works have approached this subject, proposing resonance damping passively [1,2,6,7,14,18], actively [8,9,10,11,12,28,29], or without any damping [13]. In spite of passive damping resulting in ohmic losses, in this work it was adopted because of its robustness and simplicity.

The developed methodology results in a set of $L_c$, $L_g$ and $C_f$ that meet standard restrictions. Given a converter with the specifications shown in

Table 1. Converter specifications.

Parameter	Value
Rated power	15 kW
Switching frequency	20 kHz
AC side voltage	127 V/60 Hz
DC side voltage	450 V

, the resulting inductances are illustrated in Figure 3, for a sweep of $C_f$ from 1.8% to 6.7% of $C_b$. The values of $L_c$ and $L_g$ are plotted as a function of $I_{c,f_s}$ normalized with respect to the amplitude of the low frequency component ($I_{c,f_s}/I_{c,lf}$). This ratio is varied from 7% to 27%. The values chosen for the sweep of $C_f$ and $I_{c,f_s}/I_{c,lf}$ may vary according to the rated power of the converter and component availability. In Figure 3, the inverse proportion of $L_c$ and $L_g$ is observed, and how the increase of $C_f$ reduces the value of $L_g$ required to meet the standard.

3. Filter Hardware Design

Typically, LCL filter design methodologies are limited to the determination of electrical parameters of capacitance and inductance. These are seldom considered in conjunction with the technologies that will be used to construct the filter. The process of designing the components involves adequately modeling the particular characteristics of each technology. The combined analysis of the parametric and hardware design is proposed, in order to determine the optimal relation or compromise for LCL filter losses and volume, and capacitor lifetimes of $C_f$ and $C_{bus}$.

3.1. Inductor Sizing

In the developed methodology, different magnetic material technologies are considered for the construction of the inductors. To determine the volume and losses of the LCL filter inductors, the design is performed considering three magnetic core technologies for $L_g$ and $L_c$: non-grain oriented silicon steel (NGO steel) [30], for its low cost and high magnetic flux density; Kool Mµ [31], for its relatively high magnetic flux density, but lower core losses than silicon steel; and 3C92 ferrite [32], for its low magnetic losses.

A database is built to compare the design of each inductor using these technologies. It contains 21 sizes of NGO steel sheet (EI geometry), with lengths ranging from 14 mm to 300 mm; 35 sizes of Kool Mµ core (toroid geometry), considering up to 5 stacked cores, totaling 175 possible core sizes, with relative magnetic permeabilities ranging from 26 to 125; and 28 sizes of 3C92 ferrite (EE geometry), considering up to 5 stacked cores, totaling 140 possible solutions. For conductors, solid copper wires are considered for $L_g$ and stranded wire for $L_c$, because the latter operates with high frequency.

A step-by-step procedure for the design of each inductor is shown in Appendix A. By using the proposed strategy for inductor sizing, their design will be limited by temperature rise, as a function of copper and core losses. As an indirect consequence of designing the inductors for the smallest possible volume, as is intended in the proposed methodology, when considering losses and heating, the inductor must also have low losses, in order to limit temperature rise.

3.2. Capacitor Losses and Lifetime

To achieve an optimized LCL filter, it is necessary that the capacitors be designed considering metrics that go beyond the traditional approach of simply defining the total required capacitance. While the capacitor losses can be used as a metric, a more useful parameter is the estimated capacitor lifetime. This allows a design choice that brings the best cost-benefit considering the system lifetime, since capacitors are notoriously known for being one of the electronic components most prone to failure [33].

The capacitor loss model is approximated by considering only its equivalent series resistance (ESR). This value is obtained from manufacturer datasheets, valid for steady state operation, and is a function of the frequency. The ESR is multiplied by the capacitor current harmonic spectrum, and by summing the individual contribution of each harmonic, the total electrical loss in the capacitor is obtained. Thus, for both $C_f$ and $C_{bus}$, losses ($P_C$) and temperature ($T_C$) are determined as:

$$\begin{array}{c}{P}_C=\sum _{i=1}^{\infty }{I_{C,i}}^2·ES{R}_i\left(T_C\right)\end{array}$$

(7)

$$\begin{array}{c}{T}_C=P_C{R}_{Th}+T_{amb}\end{array}$$

(8)

where $I_{C,i}$ is the RMS amplitude of the ith current harmonic and $ES{R}_i$ its corresponding ESR, that varies with temperature. $R_{Th}$ is the total thermal resistance of the capacitor, given by the manufacturer, and $T_{amb}$ the ambient temperature. When there are capacitors in parallel in the DC bus, the current $I_C$ is split.

Since losses and temperature are interdependent, $P_C$ and $T_C$ are determined iteratively. The initial temperature used to determine $P_C$ is $T_C=T_{amb}$; with this value, the $ES{R}_i$ are determined, and $P_C$ is calculated, with which a new $T_C$ is estimated; this process is repeated until the change in $T_C$ between iterations is below 1%. Only the thermal equilibrium state is analyzed.

The $T_{amb}$ to be considered in the loss and lifetime calculations will depend on the positioning of heat sources around the converter and filter, and the type of cooling system employed. This determination is complex and beyond the scope of this work. With this in mind, it is assumed that only natural convection is present and that $T_{amb}=50{}^{\circ }$C.

One of the main reasons for capacitor failure is the degradation of its dielectric, caused by voltage and temperature stresses building up over time. Thus, it is possible to estimate lifetime using a parameterized model, created from statistical failure data for each component under stress conditions [20,34].

Each capacitor technology has particular characteristics that influence its behavior in terms of losses and lifetime. For the hardware of the filter, film capacitors (C4AF series [35]) are chosen, due to its advantages in terms of cost and volume. For similar reasons, electrolytic capacitors (Type DCMC [36]) are chosen for the DC bus.

Given a determined electrothermal stress, the lifetime ($L{t}_{C_f}$) of the film capacitor $C_f$ is [20]:

$$L{t}_{C_f}=L{t}_{r_f}{2}^{0.1\left(T_{r_f}-T_{c_f}\right)}{\left(\frac{V_{r_f}}{V_{C_f}}\right)}^{n_{C_f}}$$

(9)

where $L{t}_{r_f}$ is the rated lifetime of the film capacitor, $V_{r_f}$ and $T_{r_f}$ its rated voltage and temperature, $V_{C_f}$ the voltage over $C_f$, and $n_{C_f}$ its voltage stress coefficient.

The lifetime ($L{t}_{C_{bus}}$) of an electrolytic capacitor ($C_{bus}$) is [20]:

$$L{t}_{C_{bus}}=L{t}_r{2}^{0.1\left(T_r-T_{amb}\right)}{2}^{\left(1-{\left(I_{C_{bus}}/I_r\right)}^2\right)·\frac{\Delta T_r}{n_1}}{\left(\frac{V_r}{V_{C_{bus}}}\right)}^{n_2}$$

(10)

where $L{t}_r$ is the rated lifetime for the electrolytic capacitor, $T_r$ its rated temperature, $V_r$ its rated voltage, $V_{C_{bus}}$ the voltage over $C_{bus}$, $n_2$ the voltage stress factor, $I_{C_{bus}}$ the capacitor current, $I_r$ the rated current, $\Delta T_r$ the temperature rise at $I_r$, and $n_1$ the temperature stress coefficient. Only the nominal voltage and power levels were considered for the UPS system.

4. Application of the Proposed Methodology

To demonstrate the combination of the LCL filter parametric (Section 2) and hardware (Section 3) design methodologies, the converter specifications from Table 1 and the values of $L_g$, $L_c$ and $C_f$ shown in Figure 3 are used. The design of each component is addressed in the following sections.

4.1. Filter Inductors $L_g$ and $L_c$

The volumes of $L_g$ and $L_c$, for each magnetic material technology (NGO Steel, Kool Mµ and 3C92 ferrite) are presented in Figure 4. The technologies are being identified for each point of $I_{c,fs}/I_{c,lf}$ and $C_f$. Similar to the behavior of inductance shown in Figure 3, the volumes for $L_g$ tend to increase as $I_{c,f_s}/I_{c,lf}$ gets higher, with larger volumes associated to smaller capacitances for $C_f$. For $L_c$, the volumes tend to reduce as $I_{c,f_s}/I_{c,lf}$ gets higher.

For $L_g$, it is observed that the inductors built with 3C92 ferrite are the largest, due to their low flux density capacity. Inversely, the NGO steel inductors result in the lowest volumes due to the high flux density supported by the material. This fact makes NGO steel the most indicated for the construction of $L_g$. Kool Mµ material supports intermediate flux density levels relative to the others, and results in volumes smaller than 3C92 ferrite, but larger than NGO steel.

For $L_c$, the smallest volumes are obtained with Kool Mµ material for most points of $I_{c,f_s}/I_{c,lf}$. The inductor volumes reduce as $I_{c,f_s}/I_{c,lf}$ is increased for Kool Mµ and 3C92 ferrite cores, following the behavior of Figure 3. The opposite happens to NGO steel cores, due to the significant increase in core losses. This is predicted because the inductor is designed considering its relationship of losses, volume and temperature, as described in Appendix A. When high losses are estimated, larger cores are selected to reduce magnetic flux density, also increasing the surface area for heat transfer. Thus, volumes for $L_c$ using NGO Steel increase rather than decrease when $I_{c,f_s}/I_{c,lf}$ rises. For this same reason, at the last point of $I_{c,f_s}/I_{c,lf}$ in Figure 4, it is possible to build an $L_c$ with 3C92 ferrite core that is smaller than a Kool Mµ-built inductor: the latter material has a higher core loss characteristic than the former, which stands out as $I_{c,f_s}/I_{c,lf}$ is increased.

Based on the characteristics of each technology, the application of the proposed methodology makes it possible to select the magnetic material that will result in the smallest volume for $L_g$ and $L_c$, for the considered values of $I_{c,f_s}/I_{c,lf}$ and $C_f$. The selection of the smallest volume for $L_c$ and $L_g$ for the converter from Table 1 will result in the volumes of $L_c+L_g$ shown in Figure 5. In it, the coloration of the markers identify which magnetic material resulted in the smallest volume for each inductor. The left side of the marker corresponds to the magnetic material of $L_g$, and the right side to $L_c$.

Having a freedom of choice for combinations of L-C-L considering normative restrictions, it is demonstrated that there is a specific value of $I_{c,f_s}/I_{c,lf}$ that will result in the smallest inductor volumes.

4.2. Filter Capacitor $C_f$

The complete analysis of the LCL filter volume is done considering the contribution of $C_f$. Figure 6 shows the variation of the total volume ($C_f+L_g+L_c$) of the filter for the swept values of $I_{c,f_s}/I_{c,lf}$ and $C_f$. Similarly to Figure 5, the coloration of the markers identify which magnetic material resulted in the smallest volume for each inductor. The individual contribution of each component to the total filter volume is also shown. The combined volumes show that even if the largest capacitor values (47 µF and 55 µF) result in smallest inductor volumes (Figure 5), the intermediate value of 24.5 µF results in the smallest volume for the LCL filter (Figure 6).

The value of $I_{c,f_s}/I_{c,lf}=17\%$ minimized filter volume, which corresponds to a $\Delta$I of approximately $28\%$ of the peak value of the sinusoid. The obtained value of $L_c=0.6L_g$ differs from the recurrent decision to choose $L_c=L_g$ [1,8,15,37]. The capacitance value that minimized filter volume, $C_f=24.5$ µF, corresponds to 2.9% of $C_b$, which is in accordance to the usual $C_f\le 5\%$ of $C_b$ [6,7,9,14,15,17].

The second parameter under consideration for the LCL filter design is the filter capacitor lifetime. It is estimated using (9), resulting in Figure 7. For low $I_{c,f_s}/I_{c,lf}$, there is a longer estimated lifetime, due to the low harmonic content absorbed by the capacitor (at low $I_{c,f_s}/I_{c,lf}$ most harmonics are filtered by $L_c$). As $I_{c,f_s}/I_{c,lf}$ is increased, more harmonics are filtered by $C_f$, increasing losses and reducing lifetime. Since $R_{Th}$ and ESR are higher for the smaller capacitance values, the lifetime estimation for the 15 µF and 24.5 µF is significantly smaller than the others as $I_{c,f_s}/I_{c,lf}$ is increased.

As can be seen in Figure 7, the highest estimated lifetime for all values of $C_f$ is given at the lowest value of $I_{c,f_s}/I_{c,lf}$ (7%). If the $C_f$ value that minimizes filter volume (24.5 µF) is chosen for $I_{c,f_s}/I_{c,lf}=7\%$, the maximum $L{t}_{C_f}$ design would result in an LCL filter with a volume 9.5% higher than the minimum volume, which was obtained at $I_{c,f_s}/I_{c,lf}=17\%$. In contrast, at $I_{c,f_s}/I_{c,lf}=17\%$ the estimated lifetime is 29% smaller than at $I_{c,f_s}/I_{c,lf}=7\%$, choosing the latter could be considered a reasonable trade-off.

4.3. Bus Capacitors $C_{bus}$

The last parameter under consideration is the bus capacitor lifetime. The total required capacitance ($C_{bus}^{*}$) is calculated as a function of hold-up time [38]. The minimum capacitance of the DC Bus for the converter from Table 1 is estimated as $C_{bus}^{*}=3.76$ mF. The following combinations of parallel capacitors were considered for each half of the DC bus: $16\times 470$ µF, $4\times 1900$ µF, or $2\times 3900$ µF. Their volumes are (each bus half): 632 cm${}^3$, 352 cm${}^3$, and 374 cm${}^3$, respectively. The lifetime for each individual capacitor in the DC bus is estimated using (10), resulting in Figure 8. The variation of lifetime using the three possible combinations of parallel capacitors are plotted for comparison.

Given the tested configurations for the DC Bus, the overall best result in estimated lifetime was achieved using $4\times 1900$ µF, besides having the smallest volume. This result may seem counter-intuitive, as it is expected that when the current stresses are divided among more capacitors (e.g., $16\times 470$ µF), estimated lifetime will increase. However, taking into consideration actual capacitor $R_{Th}$, ESR and current limits, when individual lifetimes are being considered, it is slightly worse to use 470 µF capacitors than using 1900 µF, for the DCMC series [36]. This seemingly counter-intuitive result demonstrates the importance of considering individual characteristics when designing the hardware, as was similarly shown in Section 4.1 for the inductors.

Similarly to $C_f$, when $I_{c,f_s}/I_{c,lf}$ increases, the estimated lifetime of $C_{bus}$ decreases, because of the higher harmonic currents (Figure 8). $L{t}_{C_{bus}}$ is also influenced by $C_f$, with higher values increasing harmonic currents in $C_{bus}$, reducing lifetime.

As discussed in Section 4.2, when using $C_f=24.5$ µF, the minimum volume for the LCL filter was obtained with $I_{c,f_s}/I_{c,lf}=17\%$, but the volume difference to $I_{c,f_s}/I_{c,lf}=7\%$ (lowest value considered) was of 9.5%. Given the same capacitance value in the filter (24.5 µF), and with $4\times 1900$ µF in the DC bus, the difference in $L{t}_{C_{bus}}$ between $I_{c,f_s}/I_{c,lf}=17\%$ and $7\%$ is of 4.4%. This difference in lifetime is smaller than what was found for $L{t}_{C_f}$, which was of 29%. Since using $I_{c,f_s}/I_{c,lf}=7\%$ benefits both $L{t}_{C_{bus}}$ and $L{t}_{C_f}$, the possible trade-off between filter volume and capacitor lifetime, mentioned at the end of Section 4.2, may continue be considered reasonable.

5. Experimental Results

The developed methodology for the LCL filter design is validated experimentally using two metrics. The first one is verifying that the designed filter meets the normative restrictions (IEC 61000-3-4), validating the parametric design (Section 2).

The second metric is the conformity of estimated power loss to the loss measurement, corresponding to the hardware design (Section 3). Capacitor lifetimes are directly related to their losses, as given by (7) through (10); and estimating inductor losses correctly is crucial for the entire design procedure, as described in Appendix A.

A 3 kW converter is considered as the case study for experimental results. To simplify the prototype, only a single-phase (1 kW) half-bridge is built, since the topology of Figure 2 allows that the LCL filter be designed per-phase. Furthermore, as described in Section 2, the LCL filter is designed to meet normative restrictions by itself, and therefore inductances of the grid and/or transformers at the input are disregarded. To avoid these influences, the converter is operated with reversed power flow, with a DC source at the bus, and a 1 kW load in series with $L_g$ (AC side). Either way, the LCL filter is attenuating the harmonics generated by converter switching.

The test setup is shown in Figure 9. Waveforms are measured with a Tektronix MDO3034 oscilloscope, and losses are measured using a Yokogawa WT1600 power meter. Total losses are $P_{loss}=P_{in}-P_{out}$. To separate semiconductor, filter, and DC Bus losses, the MOSFET losses ($P_{MOS}$) are estimated using the method presented by [39,40]. The estimated $P_{loss}$ is equal to the sum of all estimated losses,

$$P_{loss}=P_{L_g}+P_{L_c}+P_{C_f}+P_{C_{bus}}+P_{R_f}+P_{MOS}$$

(11)

where $P_{L_g}$ and $P_{L_c}$ are the total losses (A15) estimated in the grid and converter-side inductors, $P_{C_f}$ and $P_{C_{bus}}$ the losses (7) in the filter and bus capacitors, and $P_{R_f}$ joule losses in the damping resistor ($P_{R_f}=R_f{I}_{C_f}^2$).

The converter specifications for the experimental results (single-phase) are shown in

Table 2. Converter specifications for experimental results (single-phase).

Parameter	Value
Rated power	1 kW
Switching frequency	20 kHz
AC side voltage	127 V/60 Hz
DC side voltage	430 V

. The methodology is applied considering a sweep of $C_f$ from 1.5% to 9.12% of $C_b$, and $I_{c,f_s}/I_{c,lf}$ from 3% to 17%. The resulting volumes are shown in Figure 10. The estimated lifetimes $L{t}_{C_f}$ and $L{t}_{C_{bus}}$ are shown in Figure 11. Only one 1900 µF capacitor is used for each half of the DC bus.

The filter volume is minimized with $C_f=5$ µF and $I_{c,f_s}/I_{c,lf}=7\%$, as shows Figure 10. For these values, the lifetime of $C_f$ is only 1.5% smaller than the maximum value (at $I_{c,f_s}/I_{c,lf}=3\%$), and for $C_{bus}$ the lifetime is 0.3% smaller, as shows Figure 11. Though the capacitor lifetime is not maximized in this solution, it is considered a good compromise, and more useful than selecting $I_{c,f_s}/I_{c,lf}=3\%$, whose volume is 9.5% larger.

For the chosen operating point with $C_f=5$ µF, the corresponding inductances are $L_g=423$ µH and $L_c=1.48$ mH. The filter is designed to meet the IEC 61000-3-4 standard with a safety margin of 2/3 of the maximum admissible harmonic amplitude, or $I_{g,fs}/I_{g,lf}\approx 0.4\%$.

The oscilloscope and power meter measurements are shown in Figure 12. The oscilloscope waveforms in channel 1 show the drain-to-source voltage over the MOSFET; channel 2 the AC-side voltage; channel 3 the current in $L_c$; and channel 4 the current in $L_g$. The total losses measurement is: $P_{loss}=1001.7-960.6=41.1$ W, corresponding to the reading of elements $P1-P5$. Measurements were taken at other points of the circuit: $P1-P2=22.1$ W represents the losses of the converter (MOSFET and DC Bus combined); $P2-P3=12.6$ W represent $P_{L_c}$; $P3-P4=3.3$ W represent $P_{C_f}$ and $P_{R_f}$ combined; $P4-P5=3.1$ W represent $P_{L_g}$. Estimated losses were: 3.66 W for $P_{L_g}$; 13.38 W for $P_{L_c}$; 0.10 W for $P_{C_f}$; 2.19 W for $P_{R_f}$; 16.49 W for $P_{MOS}$; and 3.50 W for $P_{C_{bus}}$, adding up to 39.32 W. The difference between the measured and estimated value is of 1.78 W, corresponding to 4.33% of the measured value.

In Figure 13 the harmonic amplitudes of current over the frequency spectrum in $L_c$ and $L_g$ are presented. The measured ratio of $I_{g,f_s}/I_{g,lf}$ is of 0.41%, close to the stipulated value of approximately 0.4%.

6. Conclusions

In this work a two-stage methodology for parametric and hardware design of LCL filters for grid-connected converters was presented. The first stage (parametric design) is based on the sweep of possible filter capacitances ($C_f$) and harmonic current content at the converter ($I_{c,f_s}$). It is employed to determine different combinations of L-C-L that meet the restrictions of the standard. The second stage (filter hardware design) determines the hardware for each combination of L-C-L that was obtained in the first stage, taking into account practical aspects and particularities of each technology.

The influence of using different technologies for the core material of the inductors of the LCL filter was discussed. It was addressed how their individual characteristics relate to the frequency and switching harmonics, distinctly influencing the final design of each inductor. A step-by-step procedure for the parametric and hardware design of the components was presented. The relationship among the value of $C_f$, the amount of harmonics absorbed by it, and how these influence the total volume of the LCL filter was also considered.

In addition to the filter volume criterion, the lifetime of the filter and bus capacitors was considered. In this way, a broader perspective design-wise was possible, where compromises between filter volume and capacitor lifetimes were discussed.

The results have shown that when using the proposed methodology, the joint analysis of the parametric and hardware designs makes it possible to identify the values of current harmonics and capacitances that minimize the filter volume, maximize the lifetimes of the capacitors, or a compromise between both, with all methods meeting the normative restrictions.