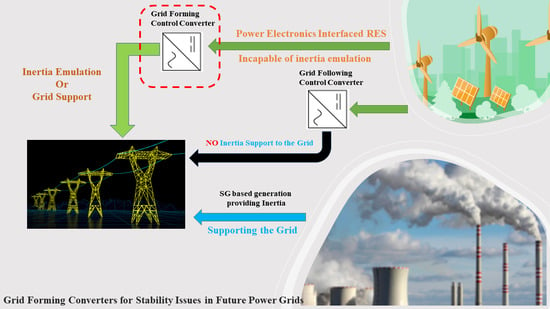
Grid-Forming Converters for Stability Issues in Future Power Grids
Abstract
:1. Introduction and Literature Review
2. Grid-Forming Converters and Power System Stability
2.1. Large-Signal Stability Issues
2.2. Frequency Stability
- Should the grid-forming controls be categorized similarly to hierarchical controls based on time scale?
- Considering the stochastic nature of RES, new dynamic models need to be derived to guarantee the system reserve and security margin.
- GFM-controlled sources can generate a fast frequency response when storage reserves are made available. What is the optimal placement amount and location of these reserves?
- Do the maximum and minimum frequency limits need to be changed for a low-inertia or converter-dominated grid?
- Does the simultaneous operation of the GFM, GFL, and SG improve the system stability or worsen it?
- What is each regulator’s optimal and maximum allowable share, such as GFL or GFM?
- How can the nature of RES (such as PV and wind) impact the frequency regulation for a GFM-controlled converter?
2.3. Voltage Stability
- When GFM replaces GFL controls on a large scale, it will shift the reactive power control from a centralized to the local level. How will it affect the system control and stability?
- How can their interaction be optimized in a hybrid system that includes both machines and GFM inverter-based sources?
- Will the combination of machines, GFL controls, and GFM controls strengthen or weaken the system’s stability? How can the optimal share of each be identified?
- How can the input and output impedances of GFM converters be modeled and characterized to improve the system’s overall dynamic response?
- Investigation of the possible issues in the implementation of VAR controls for GFM converters.
3. Grid-Forming Converters Topologies
3.1. Synchronverter
3.2. Matching Control
3.3. Virtual Oscillator Control (VOC)
3.4. Dispatchable Virtual Oscillator (dVOC)
3.5. Direct Voltage (V-f) Control
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Monti, A. Low Inertia Grids: Towards a power electronics-based power system. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ‘19 ECCE Europe), Genova, Italy, 3–5 September 2019; p. 1. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbi, G. Foundations and Challenges of Low-Inertia Systems. In Proceedings of the Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- ENTSOE—System Operation Committee (SOC). One Vision 2030 Internal Report; ENTSOE: Brussels, Belgium, 2019. [Google Scholar]
- IEA. Energy Policies of IEA Countries: Denmark 2017 Review; IEA: Paris, France, 2017; Available online: https://www.iea.org/reports/energy-policies-of-iea-countries-denmark-2017-review (accessed on 4 April 2022).
- IEA. Global Energy Review 2021; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/global-energy-review-2021 (accessed on 4 April 2022).
- Electricity Reliability Council of Texas (ERCOT). Future Ancillary Services in ERCOT; ERCOT: Austin, TX, USA, 2013. [Google Scholar]
- Matevosyan, J.; Sharma, S.; Huang, S.H.; Woodfin, D.; Ragsdale, K.; Moorty, S.; Wattles, P.; Li, W. Proposed future Ancillary Services in Electric Reliability Council of Texas. In Proceedings of the IEEE PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; p. 6. [Google Scholar]
- Julia Matevosyan-ERCOT. Inertia Trends in ERCOT. 25 February 2020. Available online: https://www.esig.energy/inertia-trends-in-ercot/ (accessed on 2 February 2022).
- National Grid ESO. O I NEEE; National Grid ESO: Warwick, UK, 2020. [Google Scholar]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of dq small-signal impedance of grid-tied inverters. IEEE Trans. Power Electron. 2015, 31, 675–687. [Google Scholar] [CrossRef]
- Pattabiraman, D.; Lasseter, R.H.; Jahns, T.M. Comparison of Grid Following and Grid Forming Control for a High Inverter Penetration Power System. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ackermann, T.; Prevost, T.; Vittal, V.; Roscoe, A.J.; Matevosyan, J.; Miller, N. Paving the Way: A Future Without Inertia Is Closer Than You Think. IEEE Power Energy Mag. 2017, 15, 61–69. [Google Scholar] [CrossRef] [Green Version]
- Ray, I. Grid-Forming Converter Control Method to Improve DC-Link Stability in Inverter-Based AC Grids. Ph.D. Thesis, The University of Tennessee, Knoxville, TN, USA, 2021. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Interconnection of two very weak AC systems by VSC-HVDC links using power-synchronization control. IEEE Trans. Power Syst. 2011, 26, 344–355. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, D.M.; Loh, P.C. Design, analysis, and realtime testing of a controller for multibus microgrid system. IEEE Trans. Power Electron. 2004, 19, 1195–1204. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vicuna, L.G.; Matas, J.; Castilla, M.; Miret, J. A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems. IEEE Trans. Power Electron. 2004, 19, 1205–1213. [Google Scholar] [CrossRef]
- Zhong, Q.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhong, Q.; Nguyen, P.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef] [Green Version]
- Johnson, B.B.; Sinha, M.; Ainsworth, N.G.; Dörfler, F.; Dhople, S.V. Synthesizing virtual oscillators to control islanded inverters. IEEE Trans. Power Electron. 2016, 31, 6002–6015. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Hug, G. Partial grid forming concept for 100% inverter-based transmission systems. In Proceedings of the 2018 IEEE Power Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Pico, H.N.V.; Johnson, B.B. Transient Stability Assessment of Multi-Machine Multi-Converter Power Systems. IEEE Trans. Power Syst. 2019, 34, 3504–3514. [Google Scholar] [CrossRef]
- Schöll, C.; Lens, H. Design- and simulation-based comparison of grid-forming converter control concepts. In Proceedings of the 20th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants (WIW 2021), Berlin, Germany, 29–30 September 2021; pp. 310–316. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.C. Small-signal modeling and parameters design for virtual synchronous generators. IEEE Trans. Ind. Electron. 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z.; Zhang, L.; Wu, K.; Hu, J. Transient stability analysis and control design of droop-controlled voltage source converters considering current limitation. IEEE Trans. Smart Grid 2019, 10, 578–591. [Google Scholar] [CrossRef]
- Khan, S.A.; Liu, C.; Ansari, J.A. Unified voltage droop control strategy for VSC-MTDC in HVDC system. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online, 2–3 July 2020; pp. 846–851. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-oriented transient stability analysis of grid-connected converters with power synchronization control. IEEE Trans. Ind. Electron. 2019, 66, 6473–6482. [Google Scholar] [CrossRef] [Green Version]
- Geng, H.; Liu, L.; Li, R.Q. Synchronization and reactive current support of PMSG-based wind farm during severe grid fault. IEEE Trans. Sustain. Energy 2018, 9, 1596–1604. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-oriented transient stability analysis of PLL-synchronized voltage-source converters. IEEE Trans. Power Electron. 2020, 35, 3573–3589. [Google Scholar] [CrossRef] [Green Version]
- Hart, P.; Lesieutre, B. Energy function for a grid-tied, droop-controlled inverter. In Proceedings of the 2014 North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014; pp. 1–6. [Google Scholar]
- Fu, X.; Sun, J.; Huang, M.; Tian, Z.; Yan, H.; Iu, H.H.C.; Hu, P.; Zha, H. Large-Signal Stability of Grid-Forming and Grid-Following Controls in Voltage Source Converter: A Comparative Study. IEEE Trans. Power Electron. 2021, 36, 7832–7840. [Google Scholar] [CrossRef]
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid Forming Converters in Renewable Energy Sources Dominated Power Grid: Control Strategy, Stability, Application, and Challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Mei, L.; Ding, L.; Wang, Z.; Cai, D.; Ding, R.; Wang, J.; Xu, H. Synchronization Stability of PLL-Based Power Converters Connected to Weak AC Grid. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 1436–1440. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Hou, X.; Han, H.; Zhong, C.; Yuan, W.; Yi, M.; Chen, Y. Improvement of transient stability in inverter-based AC microgrid via adaptive virtual inertia. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Wu, H.; Wang, X. A mode-adaptive power-angle control method for transient stability enhancement of virtual synchronous generators. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1034–1049. [Google Scholar] [CrossRef]
- Lan, Z.; Gan, D.; Shi, L.; Ni, Y. A study on the control of ac/dc power systems based on system dynamic COI. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Oureilidis, K.O.; Demoulias, C.S. A fault clearing method in converter-dominated microgrids with conventional protection means. IEEE Trans. Power Electron. 2016, 31, 4628–4640. [Google Scholar] [CrossRef]
- Paquette, A.D.; Divan, D.M. Virtual impedance current limiting for inverters in microgrids with synchronous generators. IEEE Trans. Ind. Appl. 2015, 51, 1630–1638. [Google Scholar] [CrossRef]
- Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Villegas Pico, H.N.; Seo, G.-S.; Pierre, B.J.; Ellis, A. Research Roadmap on Grid-Forming Inverters; NREL/TP-5D00-73476; National Renewable Energy Laboratory: Golden, CO, USA, 2020. [Google Scholar]
- Zografos, D. Power System Inertia Estimation and Frequency Response Assessment. Ph.D. Dissertation, KTH Royal Institute of Technology, Stockholm, Sweden, 2019. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-263786 (accessed on 5 May 2022).
- Bottrell, N.; Green, T.C. Comparison of current-limiting strategies during fault ride-through of inverters to prevent latch-up and wind-up. IEEE Trans. Power Electron. 2014, 29, 3786–3797. [Google Scholar] [CrossRef] [Green Version]
- Hou, X.; Sun, Y.; Zhang, X.; Lu, J.; Wang, P.; Guerrero, J.M. Improvement of frequency regulation in VSG-based AC microgrid via adaptive virtual inertia. IEEE Trans. Power Electron. 2020, 35, 1589–1602. [Google Scholar] [CrossRef]
- Sato, T.; Asharif, F.; Umemura, A.; Takahashi, R.; Tamura, J. Cooperative Virtual Inertia and Reactive Power Control of PMSG Wind Generator and Battery for Improving Transient Stability of Power System. In Proceedings of the 2020 IEEE International Conference on Power and Energy (PECon), Penang, Malaysia, 7–8 December 2020; pp. 101–106. [Google Scholar] [CrossRef]
- Yu, H.; Awal, M.A.; Tu, H.; Husain, I.; Lukic, S. Comparative transient stability assessment of droop and dispatchable virtual oscillator controlled gridconnected inverters. IEEE Trans. Power Electron. 2021, 36, 2119–2130. [Google Scholar] [CrossRef]
- Chen, J.; Prystupczuk, F.; O’Donnell, T. Use of voltage limits for current limitations in grid-forming converters. CSEE J. Power Energy Syst. 2020, 6, 259–269. [Google Scholar]
- Kkuni, K.V.; Yang, G. Effects of current limit for grid forming converters on transient stability: Analysis and solution. arXiv 2021, arXiv:2106.13555. [Google Scholar]
- Afshari, E.; Moradi, G.R.; Rahimi, R.; Farhangi, B.; Yang, Y.; Blaabjerg, F.; Farhangi, S. Control strategy for three-phase grid-connected PV inverters enabling current limitation under unbalanced faults. IEEE Trans. Ind. Electron. 2017, 64, 8908–8918. [Google Scholar] [CrossRef] [Green Version]
- Binu Krishnan, U.; Mija, S.J.; Cheriyan, E.P. Small signal stability analysis of droop controlled microgrid with state feedback controller. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, WA, Australia, 10–12 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fan, W.; Yan, X.; Hua, T. Adaptive parameter control strategy of VSG for improving system transient stability. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017-ECCE Asia), Kaohsiung, China, 3–7 June 2017; pp. 2053–2058. [Google Scholar]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient stability of voltage-source converters with grid-forming control: A design-oriented study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Institute of Electrical and Electronics Engineers (IEEE); North American Electric Reliability Corporation (NERC). Task Force on Short-Circuit and System Performance Impact of Inverter Based Generation. In Impact of Inverter Based Generation on Bulk Power System Dynamics and Short-Circuit Performance; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2018. [Google Scholar]
- Alegria, E.; Brown, T.; Minear, E.; Lasseter, R.H. CERTS Microgrid Demonstration with Large-Scale Energy Storage and Renewable Generation. IEEE Trans. Smart Grid 2014, 5, 937–943. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-Phase PLLs: A Review of Recent Advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Huang, S.-H.; Schmall, J.; Conto, J.; Adams, J.; Zhang, Y.; Carter, C. Voltage control challenges on weak grids with high penetration of wind generation: Ercot experience. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- IEEE Std 1204–1997; IEEE Guide for Planning DC Links Terminating at AC Locations Having Low Short-Circuit Capacities. IEEE: Piscataway, NJ, USA, 1997; pp. 1–216.
- North American Electric Reliability Corporation (NERC). Protection System Response to Power Swings; NERC System Protection and Control Subcommittee Report; NERC: Atlanta, GA, USA, 2013. [Google Scholar]
- Erickson, M.J.; Jahns, T.M.; Lasseter, R.H. Improved Power Control Bandwidth of Grid-Forming Sources in a CERTS Microgrid. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2012; pp. 2366–2373. [Google Scholar]
- Hossain, M.; Pota, H.; Issa, W.; Hossain, M. Overview of ac microgrid controls with inverter-interfaced generations. Energies 2017, 10, 1300. [Google Scholar] [CrossRef]
- NERC. Inverter-Based Resource Performance Guideline; NERC: Atlanta, GA, USA, 2018. [Google Scholar]
- Deng, Z.; Wang, H.; Qin, Y.; Zhang, J.; Zhu, C.; Cai, X. Matching-Control of Wind Power System Based on Current Source Converter. In Proceedings of the 10th Renewable Power Generation Conference (RPG 2021), Online, 14–15 October 2021; pp. 144–150. [Google Scholar] [CrossRef]
- Dhople, S.V.; Johnson, B.B.; Hamadeh, A.O. Virtual Oscillator Control for voltage source inverters. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 1359–1363. [Google Scholar] [CrossRef]
- Seo, G.-S.; Colombino, M.; Subotic, I.; Johnson, B.; Gross, D.; Dorfler, F. Dispatchable Virtual Oscillator Control for Decentralized Inverter-Dominated Power Systems: Analysis and Experiments. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; National Renewable Energy Laboratory: Golden, CO, USA, 2019. [Google Scholar]
- Tayyebi, A.; Dörfler, F.; Kupzog, F.; Miletic, Z.; Hribernik, W. Grid-forming converters—Inevitability, control strategies and challenges in future grid applications. In Proceedings of the Workshop on Microgrids and Local Energy Communities (CIRED 2018), Ljubljana, Slovenia, 7–8 June 2018. [Google Scholar]
- Kim, J.; Guerrero, J.M.; Rodriguez, P.; Teodorescu, R.; Nam, K. Mode Adaptive Droop Control With Virtual Output Impedances for an Inverter-Based Flexible AC Microgrid. IEEE Trans. Power Electron. 2011, 26, 689–701. [Google Scholar] [CrossRef]
- Hesse, R.; Turschner, D.; Beck, H. Micro grid stabilization using the virtual synchronous machine (VISMA). Renew. Energy Power Qual. J. 2009, 1, 676–681. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H. Dynamic properties of the virtual synchronous machine (VISMA). Renew. Energy Power Qual. J. 2011, 11, 755–759. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H. Comparison of methods for implementing virtual synchronous machine on inverters. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’12), Santiago de Compostela, Spain, 28–30 March 2012; pp. 734–739. [Google Scholar]
- Hirase, Y.; Abe, K.; Sugimoto, K.; Shindo, Y. A grid connected inverter with virtual synchronous generator684 model of algebraic type. IEEE Trans. Power Energy 2012, 132, 371–380. [Google Scholar] [CrossRef]
- Li, M.; Huang, W.; Tai, N.; Duan, D. Virtual Inertia Control of the Virtual Synchronous Generator: A Review. arXiv 2021, arXiv:2109.07590. [Google Scholar]
- Liu, J.; Miura, Y.; Ise, T. Dynamic characteristics and stability comparisons between virtual synchronous generator and droop control in inverter-based distributed generators. In Proceedings of the 2014 International Power Electronics Conference (IPEC—Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 1536–1543. [Google Scholar]
- Ashabani, M.; Freijedo, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-Less Converters with Auto-Synchronization and Emulated Inertia Capability. IEEE Trans. Smart Grid 2016, 7, 1660–1674. [Google Scholar] [CrossRef] [Green Version]
- Driesen, J.; Visscher, K. Virtual synchronous generators. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–3. [Google Scholar]
- Morren, J.; Pierik, J.; de Haan, S.W.H. Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Günther, K.; Sourkounis, C. Investigation of Virtual Synchronous Machine Control for the Grid-Side Converter of Wind Turbines with Permanently Excited Synchronous Generator. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 2395–2401. [Google Scholar]
- Shang, L.; Hu, J.; Yuan, X.; Huang, Y. Improved virtual synchronous control for grid-connected VSCs under grid voltage unbalanced conditions. J. Mod. Power Syst. Clean Energy 2019, 7, 174–185. [Google Scholar] [CrossRef]


















| Time and Date | 2013 14 March 2013 3:00 a.m. | 2014 30 March 2014 3:00 a.m. | 2015 25 November 2015 2:00 a.m. | 2016 10 April 2016 2:00 a.m. | 2017 27 October 2017 4:00 a.m. | 2018 3 November 2018 3:30 a.m. |
|---|---|---|---|---|---|---|
| Min Synch Inertia (GW’s) | 132 | 135 | 152 | 143 | 130 | 128.8 |
| System Load at Min. Synch Inertia (MW) | 24,726 | 24,540 | 27,190 | 27,831 | 28,425 | 28,397 |
| Non-Synch Gen. in % of system Load | 31 | 34 | 42 | 47 | 54 | 53 |
| Priority Rank | Issues |
|---|---|
| 1 | Inertia |
| 2 | Transient stability |
| 3 | Variety of load during frequency containment |
| 4 | Power converters integration |
| 5 | Lack of reactive power |
| 6 | Power oscillations |
| 7 | Voltage and frequency dip |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, S.A.; Wang, M.; Su, W.; Liu, G.; Chaturvedi, S. Grid-Forming Converters for Stability Issues in Future Power Grids. Energies 2022, 15, 4937. https://doi.org/10.3390/en15144937
Khan SA, Wang M, Su W, Liu G, Chaturvedi S. Grid-Forming Converters for Stability Issues in Future Power Grids. Energies. 2022; 15(14):4937. https://doi.org/10.3390/en15144937
Chicago/Turabian StyleKhan, Shahid Aziz, Mengqi Wang, Wencong Su, Guanliang Liu, and Shivam Chaturvedi. 2022. "Grid-Forming Converters for Stability Issues in Future Power Grids" Energies 15, no. 14: 4937. https://doi.org/10.3390/en15144937
APA StyleKhan, S. A., Wang, M., Su, W., Liu, G., & Chaturvedi, S. (2022). Grid-Forming Converters for Stability Issues in Future Power Grids. Energies, 15(14), 4937. https://doi.org/10.3390/en15144937