Gas Hold-Up in Vessel with Dual Impellers and Different Baffles
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
- -
- impeller speed n;
- -
- superficial gas velocity wog;
- -
- the type of the upper impeller (A315(L)-RT(U), A315(L)-CD6(U), A315(L)-HE3(U));
- -
- the type of the lower agitator (RT(L)-A315(U), CD6(L)-A315(U));
- -
- replacement of two impellers on the shaft (A315(L)-RT(U), RT(L)-A315(U) or A315(L)-CD6(U), CD6(L)-A315(U));
- -
- type of liquid in the system (distilled water, aqueous solutions NaCl of concentration c = 0.4 kmol/m3 and c = 0.8 kmol/m3, aqueous solution of sucrose of concentration c = 2.5% mass., 5% mass., 5% mass. aqueous solution of sucrose of concentration and yeast suspension concentration ys = 1% mass.);
- -
- type of baffles (four planar standard baffles or 24 vertical tubular baffles) on gas hold-up.
3.1. Analysis of the Results Obtained in the Vessel with Planar Baffles
3.2. Analysis of the Results Obtained in the Vessel with Vertical Tubular Baffles
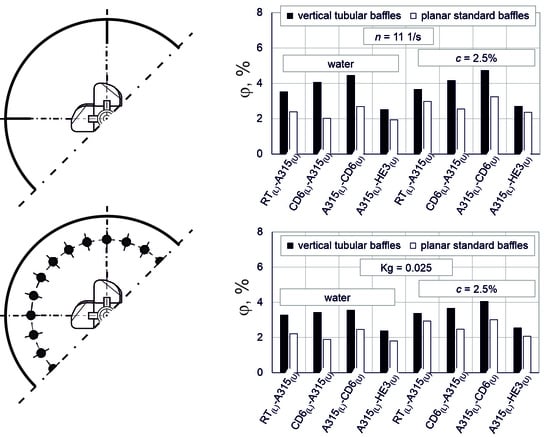
3.3. Comparison of the Results Obtained in the Vessels with Planar Baffles and Vertical Tubular Baffles
4. Conclusions
- For all tank–baffle–impeller configurations, gas hold-up φ increases with an increase in impeller speed and with an increase in the superficial gas velocity in the vessel. The influence of impeller speed and superficial gas velocity in the vessel on the value of gas hold-up φ depends on the configurations of the impeller, the type of baffles and the type of liquid in the system.
- Regardless of the type of baffles used in the tests, higher values of φ were obtained when the A315 impeller was installed on the lower shaft. In this case, higher values of gas hold-up φ, both for the vessels with planar or vertical tubular baffles, were obtained when the upper shaft was equipped with an impeller generating radial–axial circulation (RT or CD6) compared to the values of φ obtained when the upper impeller used was an HE3 impeller.
- The influence of the lower impeller on gas hold-up decreased with an increase in superficial gas velocity in the vessel with four planar baffles. The opposite tendency could be noticed in the case when 24 vertical tubular baffles were installed in the vessel. Then, they increased differently between the tested systems with an increase in superficial gas velocity in the vessel.
- Adding electrolytes or sucrose to the water–air system increases the value of gas hold-up φ. On the other hand, when yeast suspension was added to the system of aqueous sucrose solution with air, the value of φ decreased. The rheological properties of the fluid may affect the reduction in gas hold-up values for a three-phase system compared to two-phase systems. In the analyzed two-phase systems, the liquids occurring in them can be classified as Newtonian liquids, whereas the three-phase system in which yeast was added to the aqueous sucrose solution showed the properties of a non-Newtonian fluid.
- Comparing the values of critical impellers speed for both tank–baffle configurations, it was found that good dispersion was obtained faster for the system with 24 vertical tubular baffles when the A315 impeller was installed as the lower impeller. In the situation when the A315 impeller was mounted in the upper position, good dispersion was obtained when four planar baffles were installed in the vessel.
- In all the analyzed cases, assuming stability of other parameters, higher values of gas hold-up were obtained for the vessel with 24 vertical tubular baffles compared to the vessel with four planar standard baffles.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | length of the impeller blade [m] |
| B | width of the baffle [m] |
| b | width of the impeller blade [m] |
| c | concentration [% mass., kmol/m3] |
| D | inner diameter of the vessel [m] |
| DB | diameter of the tubular coil (baffles) [m] |
| d | diameter of the impeller [m] |
| dg | sparger diameter [m] |
| do | holes on the sparger [m] |
| e | off-bottom clearance of gas sparger [m] |
| f | activity |
| H | liquid height in the vessel [m] |
| hL | distance between lower impeller and bottom of the vessel [m] |
| hU | distance between upper impeller and bottom of the vessel [m] |
| hg−L | height of a gas–liquid mixture in the vessel [m] |
| i | number of holes on the ring sparger |
| J | number of baffles |
| n | impeller speed [1/s] |
| R | gas constant, J/molK |
| r | radius of curvature of the impeller blade |
| T | temperature [K] |
| gas flow rate [m3/s] | |
| wog | superficial gas velocity, [m/s] |
| Y | parameter |
| ys | yeast concentration [% mass.] |
| Z | number of impeller blades |
| Greek symbols | |
| β | pitch of the impeller blade [deg] |
| μ | dynamic viscosity of the liquid [Pas] |
| φ | gas hold-up |
| ρ | density of the liquid [kg/m3] |
| σ | surface tension [N/m] |
| Subscripts | |
| g | refers to gas phase |
| l | refers to liquid phase |
| L | refers to lower impeller |
| U | refers to upper impeller |
References
- Stręk, F. Agitation and Agitated Vessels; WNT: Warszawa, Poland, 1981. (In Polish) [Google Scholar]
- Kamieński, J. Agitation of Multiphase Systems; WNT: Warszawa, Poland, 2004. (In Polish) [Google Scholar]
- Chinnasamy, G.; Kaliannan, S.; Eldho, A.; Nadarajan, D. Development and performance analysis of a novel agitated vessel. Korean J. Chem. Eng. 2016, 33, 1181–1185. [Google Scholar] [CrossRef]
- Khalili, F.; Nasr, M.R.J.; Kazemzadeh, A.; Ein-Mozaffari, F. Analysis of gas holdup and bubble behavior in a biopolymer solution inside a bioreactor using tomography and dynamic gas disengagement techniques. J. Chem. Technol. Biotechnol. 2018, 93, 340–349. [Google Scholar] [CrossRef]
- Liu, B.; Zheng, Y.; Cheng, R.; Xu, Z.; Wang, M.; Jin, Z. Experimental study on gas-liquid dispersion and mass transfer in shear-thinning system with coaxial mixer. Chin. J. Chem. Eng. 2018, 26, 1785–1791. [Google Scholar] [CrossRef]
- Major-Godlewska, M.; Radecki, D. Experimental analysis of gas hold-up for gas-liquid system agitated in a vessel equipped with two impellers and vertical tubular baffles. Pol. J. Chem. Technol. 2018, 20, 7–12. [Google Scholar] [CrossRef] [Green Version]
- Cudak, M. The effect of vessel scale on gas hold-up in gas-liquid systems. Chem. Process Eng. 2020, 41, 241–256. [Google Scholar] [CrossRef]
- Barros, P.A.; Ein-Mozaffari, F.; Lohi, A. Gas Dispersion in Non-Newtonian Fluid with Mechanically Agitated Systems: A review. Processes 2022, 10, 275. [Google Scholar] [CrossRef]
- Major-Godlewska, M.; Karcz, J. Process characteristics for a gas-liquid system agitated in a vessel equipped with a turbine impeller and tubular baffles. Chem. Pap. 2011, 65, 132–138. [Google Scholar] [CrossRef]
- Major-Godlewska, M.; Karcz, J. Agitation of a gas–solid–liquid system in a vessel with high-speed impeller and vertical tubular coil. Chem. Pap. 2012, 66, 566–573. [Google Scholar] [CrossRef]
- Kiełbus-Rąpała, A.; Karcz, J. Experimental analysis of the hydrodynamics of a three-phase system in a vessel with two impellers. Chem. Pap. 2012, 66, 574–582. [Google Scholar] [CrossRef]
- Jamshed, A.; Cooke, M.; Ren, Z.; Rodgers, T.L. Gas–liquid mixing in dual agitated vessels in the heterogeneous regime. Chem. Eng. Res. Des. 2018, 133, 55–69. [Google Scholar] [CrossRef]
- de Jesus, S.S.; Moreira Neto, J.; Filho, R.M. Hydrodynamics and mass transfer in bubble column, conventional airlift, stirred airlift and stirred tank bioreactors, using viscous fluid: A comparative study. Biochem. Eng. J. 2017, 118, 70–81. [Google Scholar] [CrossRef]
- Cudak, M. Hydrodynamic characteristics of mechanically agitated air-aqueous sucrose solutions. Chem. Process Eng. 2014, 35, 97–107. [Google Scholar] [CrossRef] [Green Version]
- Jamshidzadeh, M.; Ein-Mozaffari, F.; Lohi, A. Local and overall gas holdup in an aerated coaxial mixing system containing a non-Newtonian fluid. AIChE J. 2020, 66, e17016. [Google Scholar] [CrossRef]
- Saravanan, K.; Ramamurthy, V.; Chandramohan, K. Gas hold-up in multiple impeller agitated vessels. Mod. Appl. Sci. 2009, 3, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Karcz, J.; Szoplik, J.; Major-Godlewska, M.; Cudak, M.; Kiełbus-Rąpała, A. Agitation efficiency of different physical systems. Chem. Process Eng. 2021, 41, 139–156. [Google Scholar] [CrossRef]
- Busciglio, A.; Grisafi, F.; Scargiali, F.; Brucata, A. On the measurement of local gas hold-up, interfacial area and bubble size distribution in gas-liquid contactors via light sheet and image analysis: Imaging technique and experimental results. Chem. Eng. Sci. 2013, 102, 551–566. [Google Scholar] [CrossRef]
- Wan, X.; Takahata, Y.; Takahashi, K. Power consumption and gas-liquid dispersion in turbulently agitated vessels with vertical dual-array tubular coil baffle. Chem. Pap. 2016, 70, 445–453. [Google Scholar] [CrossRef]
- Wan, X.; Takahata, Y.; Takahashi, K. Power consumption, gas holdup, and mass-transfer coefficient of triple-impeller configurations in a stirred vessels with vertical tubular coils. Can. J. Chem. Eng. 2016, 94, 349–354. [Google Scholar] [CrossRef]
- Petricek, R.; Moucha, T.; Rejl, F.J.; Valenz, L.; Haidl, J.; Cmelikova, T. Volumetric mass transfer coefficient, power input and gas hold-up in viscous liquid in mechanically agitated fermenters. Measurements and scale-up. Int. J. Heat Mass Transf. 2018, 124, 1117–1135. [Google Scholar] [CrossRef]
- Amiraftabi, M.; Khiadani, M.; Mohammed, H.A. Performance of a dual helical ribbon impeller in a two-phase (gas-liquid) stirred tank reactor. Chem. Eng. Process. Process Intensif. 2020, 148, 107811. [Google Scholar] [CrossRef]
- Liu, B.; Xiao, Q.; Gao, P.; Sunder, B.; Fan, F. Investigation of gas–liquid dispersion and mass transfer performance of wide-viscosity-range impellers in water solutions of xanthan gum. Chem. Eng. Res. Des. 2020, 154, 60–69. [Google Scholar] [CrossRef]
- Bao, Y.; Yang, J.; Wang, B.; Gao, Z. Influence of impeller diameter on local gas dispersion properties in a sparged multi-impeller stirred tank. Chin. J. Chem. Eng. 2015, 23, 615–622. [Google Scholar] [CrossRef]
- Busciglio, A.; Opletal, M.; Moucha, T.; Montante, G.; Paglianti, A. Measurement of gas hold-up distribution in stirred vessels equipped with pitched blade turbines by means of Electrical Resistance Tomography. Chem. Eng. Trans. 2017, 57, 1273–1278. [Google Scholar] [CrossRef]
- Machoň, V.; Vlček, J.; Kudrna, V. Gas hold-up in agitated aqueous solutions of strong inorganic salts. Collect. Czechoslov. Chem. Commun. 1978, 43, 593–603. [Google Scholar] [CrossRef]
- Lee, J.C.; Meyrick, D.L. Gas–Liquid interfacial areas in salt solutions in an agitated tank. Trans. Inst. Chem. Eng. 1970, 48, 37–45. [Google Scholar]
- Cudak, M. The gas hold-up for the gas-liquid system in a vessel with two impellers. Inż. Ap. Chem. 2018, 57, 93–94. (In Polish) [Google Scholar]












| No. | Impeller | a/d | b/d | Z | β | r |
|---|---|---|---|---|---|---|
| 1. | Rushton turbine (RT) | 0.25 | 0.2 | 6 | - | |
| 2. | Smith turbine (CD6) | 0.25 | 0.2 | 6 | b/2 | |
| 3. | A315 | - | 0.34 | 4 | 45 | |
| 4. | HE3 | - | 0.2 | 3 | 30 |
| Impeller Configuration | C | a | b | e | g | ±Δ, % | Range |
|---|---|---|---|---|---|---|---|
| A315(L)-CD6(U) | 3.44 × 10−4 | 0.63 | 0.93 | 10.84 | −13.10 | 7 | Kg ∈ <1.94 × 10−2–7.20 × 10−2> We ∈ <653–2117> |
| CD6(L)-A315(U) | 7.62 × 10−4 | 0.82 | 0.89 | 9.64 | −7.93 | 6 | Kg ∈ <1.94 × 10−2–7.78 × 10−2> We ∈ <600–2117> |
| RT(L)-A315(U) | 7.64 × 10−4 | 0.72 | 0.85 | 9.59 | −24.68 | 5 | Kg ∈ <1.99 × 10−2–6.48 × 10−2> We ∈ <709–2112> |
| A315(L)-RT(u) | 4.47 × 10−4 | 0.49 | 0.84 | 11.70 | −17.98 | 8 | Kg ∈ <1.99 × 10−2–7.20 × 10−2> We ∈ <500–2117> |
| A315(L)-HE3(U) | 3.69 × 10−4 | 0.66 | 0.89 | 10.39 | −4.55 | 8 | Kg ∈ <1.94 × 10−2–6.94 × 10−2> We ∈ <767–2117> |
| Impeller Configuration | C | a | b | d | ±Δ, % | Range | Gas–Liquid System |
|---|---|---|---|---|---|---|---|
| A315(L)-CD6(u) | 1.7 × 10−4 | 0.4 | 0.971 | 1 | 10% | Kg ∈ <8,84 × 10−3–64.8 × 10−3>; We ∈ <476–2551>; Y = 1 | Air–Water |
| Kg ∈ <8.84 × 10−3–70.69 × 10−3>; We ∈ <428–2556>; Y = 1.36 | Air–NaCl c = 0.4 kmol/m3 | ||||||
| Kg ∈ <8.84 × 10−3–77.76 × 10−3>; We ∈ <431–2577>; Y = 1.6 | Air–NaCl c = 0.8 kmol/m3 | ||||||
| CD6(L)-A315(U) | 4.35 × 10−4 | 0.533 | 0.9 | 0.95 | 8% | Kg ∈ <8.84 × 10−3–44.43 × 10−3>; We ∈ <896–2566>; Y = 1 | Air–Water |
| Kg ∈ <8.84 × 10−3–53.63 × 10−3>; We ∈ <584–2563>; Y = 1.36 | Air–NaCl c = 0.4 kmol/m3 | ||||||
| Kg ∈ <8.84 × 10−3–51.84 × 10−3>; We ∈ <589-2584>; Y = 1.6 | Air–NaCl c = 0.8 kmol/m3 | ||||||
| RT(L)-A315(U) | 1.64 × 10−4 | 0.426 | 0.958 | 0.8 | 6% | Kg ∈ <8.84 × 10−3–44.43 × 10−3>; We ∈ <899–2574>; Y = 1 | Air–Water |
| Kg ∈ <8.84 × 10−3–51.84 × 10−3>; We ∈<585–2567>; Y = 1.36 | Air–NaCl c = 0.4 kmol/m3 | ||||||
| Kg ∈ <8.84 × 10−3–51.84 × 10−3>; We ∈ <589–2586>; Y = 1.6 | Air–NaCl c = 0.8 kmol/m3 | ||||||
| A315(L)-HE3(U) | 1.22 × 10−4 | 0.622 | 1.053 | 0.796 | 10% | Kg ∈ <8.84 × 10−3–62.2 × 10−3>; We ∈ <430–2567>; Y = 1 | Air–Water |
| Kg ∈ <8.84 × 10−3–74 × 10−3>; We ∈ <338–2559>; Y = 1.36 | Air–NaCl c = 0.4 kmol/m3 | ||||||
| Kg ∈ <8.84 × 10−3–74 × 10−3>; We ∈ <341–2578>; Y = 1.6 | Air–NaCl c = 0.8 kmol/m3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Major-Godlewska, M.; Cudak, M. Gas Hold-Up in Vessel with Dual Impellers and Different Baffles. Energies 2022, 15, 8685. https://doi.org/10.3390/en15228685
Major-Godlewska M, Cudak M. Gas Hold-Up in Vessel with Dual Impellers and Different Baffles. Energies. 2022; 15(22):8685. https://doi.org/10.3390/en15228685
Chicago/Turabian StyleMajor-Godlewska, Marta, and Magdalena Cudak. 2022. "Gas Hold-Up in Vessel with Dual Impellers and Different Baffles" Energies 15, no. 22: 8685. https://doi.org/10.3390/en15228685
APA StyleMajor-Godlewska, M., & Cudak, M. (2022). Gas Hold-Up in Vessel with Dual Impellers and Different Baffles. Energies, 15(22), 8685. https://doi.org/10.3390/en15228685