Use of Cluster Analysis to Group Organic Shale Gas Rocks by Hydrocarbon Generation Zones
Abstract
:1. Introduction
- -
- conventional (traditional) reservoirs,
- -
- unconventional reservoirs [1].
- -
- tight gas,
- -
- shale gas,
- -
- gas reservoirs in coal seams,
- -
- reservoirs of gas trapped in hydrates [2].
- -
- variable lithology, from ‘pure’ shales, to shales with siltstone insets,
- -
- variable porosity, from relatively high, to low,
- -
- variable TOC, from high to low,
- -
- variable ratio of adsorbed to free gas, from high, to low values,
- -
- variable quartz content and type,
- -
- the rock can be solid or/and naturally fractured [6].
- -
- medium or small surface area,
- -
- medium or small thickness,
- -
- very good and good porosity of the reservoir rock,
- -
- very good and good permeability of the reservoir rock,
- -
- high and medium well outputs [7].
- -
- very large or large surface area,
- -
- large and medium thickness,
- -
- low porosity of the reservoir rock,
- -
- very low permeability of the reservoir rock,
- -
- -
- horizontal well technology,
- -
- slim hole technology,
- -
- multi-section fracturing technology [12].
- -
- neural networks, which are applied to analyzea large amount of data on geology, geophysics, and extraction,
- -
- genetic algorithms, which are used to analyze geological and petrophysical data, for reservoir simulations and to plan the fracturing procedures,
- -
- fuzzy set logic, which is employed for petrophysical analyses, characterization of reservoir parameters, drilling exploration of reservoirs, planning the stimulation procedures, increasing the depletion ratio of the reservoirs, and for analyses supporting the making of investment decisions.
2. Materials and Methods
2.1. Materials
2.2. Methods
- optimizing-iterative, involving the division of a set of objects into a specified number of k subsets, following one of the optimising criteria:
- -
- K-means—the groups are represented by a ‘center of gravity’.
- -
- K-medoids—the groups are represented by one of the objects.
- hierarchical, under which clusters of a higher level contain clusters of a lower level. Hierarchical methods include agglomerative and divisive techniques.
- selecting the initial set of clusters,
- finding the closest pair of clusters and merging them into one,
- repeating step 2 until fulfilling the rule of completion.
- -
- the lack of cluster pairs located less than a given threshold distance apart (dmax),
- -
- merging of all clusters into a single set.
- -
- Euclidean distance described by Formula (1):
- -
- City block (Manhattan) distance described by Formula (2):
- -
- Chebyshev distance described by Formula (3) [42]:
- The nearest neighbor method (single linkage)—the distance between clusters is the distance between the two closest objects.
- The farthest neighbor method (complete linkage)—the distance between clusters is the distance between the two most distant objects.
- The median method—the distance between two clusters is the median of the distance between the units of the first and the second cluster.
- The group average method—the distance between two clusters is the average distance between the units of the first and the second cluster.
- The center of gravity method—the distance between two clusters is the distance between the centres of gravity of the first and the second cluster.
- The Ward method—sampling the merging of all cluster pairs and selecting such merging in which the variance of distance inside a formed cluster is the smallest.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| TOC | total organic carbon, % by weight |
| Tmax | temperature at which the maximum quantity of hydrocarbons is produced during kerogen cracking, °C |
| S1 | free hydrocarbon content, mg HC/g of rock |
| S2 | amount of hydrocarbons released during kerogen cracking, mg HC/g of rock |
| HI | hydrogen index, mg HC/g TOC |
| OI | oxygen index, mg CO2/g TOC |
| Ro | vitrinite reflectance, % |
| S | standard deviations were calculated for the mean values of Ro, % |
| dmax | maximum distance between the objects described by the standardized data |
References
- Mandal, P.P.; Rezaee, R.; Emelyanova, I. Ensemble Learning for Predicting TOC from Well-Logs of the Unconventional Goldwyer Shale. Energies 2021, 15, 216. [Google Scholar] [CrossRef]
- Holditch, S.A. Tight Gas Sands. J. Pet. Technol. 2006, 58, 86–93. [Google Scholar] [CrossRef]
- Nie, H.; Jin, Z.; Zhang, J. Characteristics of three organic matter pore types in the Wufeng-Longmaxi Shale of the Sichuan Basin, Southwest China. Sci. Rep. 2018, 8, 7014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Josh, M.; Esteban, L.; Piane, C.D.; Sarout, J.; Dewhurst, D.; Clennell, M. Laboratory characterisation of shale properties. J. Pet. Sci. Eng. 2012, 88–89, 107–124. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Slater, T.; Dowey, P.J.; Yue, S.; Rutter, E.; Taylor, K.G.; Lee, P.D. Hierarchical integration of porosity in shales. Sci. Rep. 2018, 8, 11683. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T.S. Current perspectives on gas hydrate resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Piesik-Buś, B.; Filar, B. Analysis of the current state of natural gas resources in domestic deposits and a forecast of domestic gas production until 2030. Nafta-Gaz 2016, 6, 376–382. [Google Scholar] [CrossRef]
- Song, Y.; Li, Z.; Jiang, L.; Hong, F. The concept and the accumulation characteristics of unconventional hydrocarbon resources. Pet. Sci. 2015, 12, 563–572. [Google Scholar] [CrossRef] [Green Version]
- Das, B.; Chatterjee, R. Mapping of porepressure, in-situ stress and brittleness in unconventional shale reservoir of Krishna-Godavari basin. J. Nat. Gas Sci. Eng. 2018, 50, 74–89. [Google Scholar] [CrossRef]
- Piane, C.D.; Almqvist, B.S.; MacRae, C.; Torpy, A.; Mory, A.J.; Dewhurst, D. Texture and diagenesis of Ordovician shale from the Canning Basin, Western Australia: Implications for elastic anisotropy and geomechanical properties. Mar. Pet. Geol. 2015, 59, 56–71. [Google Scholar] [CrossRef]
- Rezaee, R. (Ed.) . Fundamentals of Gas Shale Reservoirs; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Xie, J. Rapid shale gas development accelerated by the progress in key technologies: A case study of the Changning–Weiyuan National Shale Gas Demonstration Zone. Nat. GasInd. B 2018, 5, 283–292. [Google Scholar] [CrossRef]
- Adamus, W.; Florkowski, W.J. The evolution of shale gas development and energy security in Poland: Presenting a hierarchical choice of priorities. Energy Res. Soc. Sci. 2016, 20, 168–178. [Google Scholar] [CrossRef]
- Lozano-Maya, J.R. Looking through the prism of shale gas development: Towards a holistic framework for analysis. Energy Res. Soc. Sci. 2016, 20, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Syed, F.I.; Muther, T.; Dahaghi, A.K.; Negahban, S. AI/ML assisted shale gas production performance evaluation. J. Pet. Explor. Prod. Technol. 2021, 11, 3509–3519. [Google Scholar] [CrossRef]
- Sowiżdżał, K.; Słoczyński, T.; Stadtműller, M.; Kaczmarczyk, W. Lower Palaeozoic petroleum systems of the Baltic Basin in northern Poland: A 3D basin modeling study of selected areas (onshore and offshore). Interpretation 2018, 6, SH117–SH132. [Google Scholar] [CrossRef]
- Poprawa, P. Lower Paleozoic oil and gas shale in the Baltic-Podlasie-Lublin Basin (central and eastern Europe)—Areview. Geol. Q. 2020, 64, 515. [Google Scholar] [CrossRef]
- Mroczkowska-Szerszeń, M.; Ziemianin, K.; Brzuszek, P.; Matyasik, I.; Jankowski, L. The organic matter type in the shale rock samples assessed by FTIR-ART analyses. Nafta-Gaz 2015, 6, 361–369. [Google Scholar]
- Botor, D. Hydrocarbon generation in the Upper Cambrian—Lower Silurian source rocks of the Baltic Basin (Poland), implications for shale gas exploration. In Proceedings of the 16-th International Scientific GeoConference SGEM, Vienna, Austria, 2–5 November 2016; Book1, Oil and Gas Section. pp. 127–134. [Google Scholar] [CrossRef]
- Botor, D.; Kotarba, M.; Kosakowski, P. Petroleum generation in the Carboniferous strata of the Lublin Trough (Poland): An integrated geochemical and numerical modelling approach. Org. Geochem. 2002, 33, 461–476. [Google Scholar] [CrossRef]
- Kosakowski, P.; Wróbel, M.; Poprawa, P. Hydrocarbon generation and expulsion modelling of the lower Paleozoic source rocks in the Polish part of the Baltic region. Geol. Q. 2010, 54, 241–256. [Google Scholar]
- Jarvie, D.M.; Hill, R.J.; Ruble, T.E.; Pollastro, R.M. Unconventional shale-gas systems: The Mississippian Barnett Shale of north-central Texas as one model for thermogenic shale-gas assessment. AAPG Bull. 2007, 91, 475–499. [Google Scholar] [CrossRef]
- Nehring-Lefeld, M.; Modliński, Z.; Swadowska, E. Thermal evolution of the Ordovician in the western margin of the East-European Platform: CAI and RO data. Geol. Q. 1997, 41, 129–137. [Google Scholar]
- Grotek, I. Origin and thermal maturity of the organic matter in the Lower Paleozoic rocks of the Pomerania Caledonides and their foreland (N Poland). Geol. Q. 1999, 43, 297–312. [Google Scholar] [CrossRef]
- Swadowska, E.; Sikorska, M. Burial history of Cambrian constrained by vitrinite-like macerals in Polish part of the East European Platform. Przegląd Geol. 1998, 46, 699–706. [Google Scholar]
- Zdanaviciute, O. Perspectives of oil field exploration in Middle Cambrian sandstones of Western Lithuania. Geologija 2005, 51, 10–18. [Google Scholar]
- Więcław, D.; Kotarba, M.J.; Kosakowski, P.; Kowalski, A.; Grotek, I. Habitat and hydrocarbon potential of the Lower Palaeozoic source rocks of the Polish part of the Baltic region. Geol. Q. 2010, 54, 159–182. [Google Scholar]
- Więcław, D.; Kosakowski, P.; Kotarba, M.J.; Koltun, Y.V.; Kowalski, A. Assessment of hydrocarbon potential of the Lower Palaeozoic strata in the Tarnogród–Stryi area (SE Poland and western Ukraine). Ann. Soc. Geol. Pol. 2012, 82, 65–80. [Google Scholar]
- Wang, P.; Peng, S. A New Scheme to Improve the Performance of Artificial Intelligence Techniques for Estimating Total Organic Carbon from Well Logs. Energies 2018, 11, 747. [Google Scholar] [CrossRef] [Green Version]
- Klaja, J.; Łykowska, G. Wyznaczenie typów petrofizycznych skał czerwonego spągowca z rejonu południowo-zachodniej części niecki poznańskiej na podstawie analizy statycznej wyników pomiarów laboratoryjnych. Nafta-Gaz 2014, 11, 757–764. [Google Scholar]
- Puskarczyk, E. Application of Multivariate Statistical Methods and Artificial Neural Network for Facies Analysis from Well Logs Data: An Example of Miocene Deposits. Energies 2020, 13, 1548. [Google Scholar] [CrossRef] [Green Version]
- Radzikowski, K.; Nowak, R.; Arabas, J.; Budak, P.; Łętkowski, P. Classification of Polish shale gas boreholes using measurement data. In Proceedings of the XXXVIII-th IEEE-SPIE Joint Symposium on Photonics, Web Engineering, Electronics for Astronomy and High Energy Physics Experiments, Wilga, Poland, 30 May–6 June 2016; Volume 10031. [Google Scholar] [CrossRef]
- Khoshbakht, F.; Mohammadnia, M. Assessment of Clustering Methods for Predicting Permeability in a Heterogeneous Carbonate Reservoir. J. Pet. Sci. Technol. 2012, 2, 50–57. [Google Scholar]
- Abdideh, M.; Ameri, A. Cluster An alysis of Petrophysical and Geological Parameters for Separating the Electrofacies of a Gas Carbonate Reservoir Sequence. Nonrenewable Resour. 2020, 29, 1843–1856. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Ali, A.Z.; Abouelresh, M.; Abdulraheem, A. Evaluation of the Total Organic Carbon (TOC) Using Different Artificial Intelligence Techniques. Sustainability 2019, 11, 5643. [Google Scholar] [CrossRef] [Green Version]
- Torghabeh, A.K.; Rezaee, R.; Harami, R.M.; Pimentel, N. Using electrofacies cluster analysis to evaluate shale-gas potential: Carynginia Formation, Perth Basin, Western Australia. Int. J. Oil Gas Coal Technol. 2015, 10, 250. [Google Scholar] [CrossRef]
- Farzi, R.; Bolandi, V. Estimation of organic facies using ensemble methods in comparison with conventional intelligent approaches: A case study of the South Pars Gas Field, Persian Gulf, Iran. Model. Earth Syst. Environ. 2016, 2, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Baiyegunhi, T.L.; Liu, K.; Gwavava, O.; Wagner, N.; Baiyegunhi, C. Geochemical Evaluation of the Cretaceous Mudrocks and Sandstones (Wackes) in the Southern Bredasdorp Basin, Offshore South Africa: Implications for Hydrocarbon Potential. Minerals 2020, 10, 595. [Google Scholar] [CrossRef]
- Kadkhodaie, A.; Sfidari, E.; Najjari, S. Comparison of intelligent and statistical clustering approaches to predicting total organic carbon using intelligent systems. J. Pet. Sci. Eng. 2012, 86–87, 190–205. [Google Scholar] [CrossRef]
- Alizadeh, B.; Najjari, S.; Kadkhodaie, A. Artificial neural network modeling and cluster analysis for organic facies and burial history estimation using well log data: A case study of the South Pars Gas Field, Persian Gulf, Iran. Comput. Geosci. 2012, 45, 261–269. [Google Scholar] [CrossRef]
- Łętkowski, P.; Gołąbek, A.; Budak, P.; Szpunar, T.; Nowak, R.; Arabas, J. Determination of the statistical similarity of the physicochemical measurement data of shale formations based on the methods of cluster analysis. Nafta-Gaz 2016, 72, 910–918. [Google Scholar] [CrossRef]
- Prasath, V.S.; Alfeilat, H.A.A.; Hassanat, A.B.; Lasassmeh, O.; Tarawneh, A.S.; Alhasanat, M.B.; Salman, H.S.E. Effects of Distance Measure Choice on KNN Classifier Performance-A Review. arXiv 2017, arXiv:1708.04321. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R. Algorithms for Clustering Data; Prentice Hall: Hoboken, NJ, USA, 1988. [Google Scholar] [CrossRef]
- Papiernik, B.; Botor, D.; Golonka, J.; Porębski, S.J. Insight from three-dimensional modelling of total organic carbon and thermal maturity. Ann. Soc. Geol. Pol. 2019, 89, 511. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, Y.; Ran, B.; Liu, W.; Li, X.; Wang, C. Chemostratigraphic Analysis of Wufeng and Longmaxi Formation in Changning, Sichuan, China: Achieved by Principal Componentand Constrained Clustering Analysis. Energies 2021, 14, 7048. [Google Scholar] [CrossRef]
- Waszkiewicz, S.; Krakowska-Madejska, P.I. Vitrinite Equivalent Reflectance Estimation from Improved Maturity Indicator and Well Logs Based on Statistical Methods. Energies 2021, 14, 6182. [Google Scholar] [CrossRef]
- Huang, X.; Gu, L.; Li, S.; Du, Y.; Liu, Y. Absolute adsorption of light hydrocarbons on organic-rich shale: An efficient determination method. Fuel 2021, 308, 121998. [Google Scholar] [CrossRef]






| Cluster No. | Number of Elements | TOC | Tmax | S1 | S2 | HI | OI | Ro | Cluster Characteristics |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 14 | 0.25 | 432 | 0.16 | 2.01 | 169.85 | 101.25 | 0.77 | Ro = 0.77% − oil window; Ro + S = 0.91% − part in the condensate window. Silurian = 57%; Ordovician = 7%; Cambrian = 36% |
| 2 | 12 | 1.31 | 449 | 1.22 | 1.43 | 22.02 | 13.04 | 1.11 | Ro = 1.11%; Ro − S = 0.95% − condensate window; Ro + S = 1.27% − part in the gas window. Silurian = 83%; Ordovician = 17%; Cambrian = 0% |
| 3 | 23 | 0.81 | 446 | 0.40 | 0.58 | 50.08 | 41.80 | 1.25 | Ro = 1.25%; Ro − S = 1.13% − condensate window; Ro + S = 1.36% − part in the gas window. Silurian = 83%; Ordovician = 13%; Cambrian = 4% |
| 4 | 5 | 6.29 | 456 | 2.27 | 5.20 | 2.96 | 2.96 | 1.30 | Ro = 1.30%; Ro − S = 1.28% − gas window. Silurian = 80%; Ordovician = 20%; Cambrian = 0% |
| 5 | 4 | 0.15 | 493 | 0.05 | 0.50 | 100.05 | 133.97 | 1.44 | Ro = 1.44%; Ro − S = 1.33% − gas window. Silurian = 0%; Ordovician = 0%; Cambrian = 100% |
| 6 | 7 | 0.46 | 425 | 1.59 | 28.05 | 351.17 | 71.98 | 0.71 | Ro = 0.71%; Ro + S = 0.78% − oil window. Silurian = 0%; Ordovician = 57%; Cambrian = 43% |
| 8 | 4 | 0.13 | 437 | 0.30 | 4.50 | 339.66 | 275.61 | 0.77 | Ro = 0.77% − oil window; Ro + S = 0.85% − part in the condensate window. Silurian = 25%; Ordovician = 0%; Cambrian = 75% |
| Mean | 1.34 | 448 | 0.86 | 6.04 | 147.97 | 91.52 | 1.05 |
| Cluster No. | Number of Elements | TOC | Tmax | S1 | S2 | HI | OI | Ro | Cluster Characteristics |
|---|---|---|---|---|---|---|---|---|---|
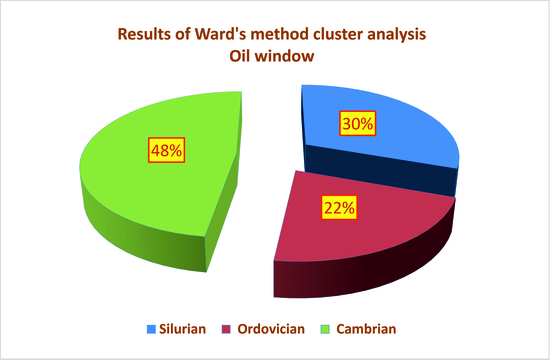
| 1 | 10 | 0.24 | 433 | 0.07 | 0.47 | 171.04 | 105.88 | 0.72 | Ro = 0.72%; Ro + S = 0.79% − oil window. Silurian = 60%; Ordovician = 10%; Cambrian = 30% |
| 2 | 14 | 1.28 | 448 | 1.14 | 1.35 | 32.17 | 13.24 | 1.11 | Ro = 1.11%; Ro − S = 0.96%; Ro + S = 1.25% − condensate window. Silurian = 86%; Ordovician = 14%; Cambrian = 0% |
| 3 | 11 | 0.59 | 435 | 0.34 | 0.46 | 77.96 | 81.40 | 1.20 | Ro = 1.20%; Ro − S = 1.07% − condensate window; Ro + S = 1.32% − part in the gas window. Silurian = 73%; Ordovician = 18%; Cambrian = 9% |
| 4 | 12 | 0.90 | 454 | 0.36 | 0.62 | 26.99 | 28.16 | 1.29 | Ro = 1.29% − gas window; Ro − S = 1.20% − part in the condensate window. Silurian = 92%; Ordovician = 8%; Cambrian = 8% |
| 5 | 5 | 6.29 | 456 | 2.27 | 5.20 | 2.96 | 2.96 | 1.30 | Ro = 1.30%; Ro − S = 1.28% − gas window. Silurian = 80%; Ordovician = 20%; Cambrian = 0% |
| 6 | 4 | 0.15 | 493 | 0.05 | 0.50 | 100.05 | 133.97 | 1.44 | Ro = 1.44%; Ro − S = 1.33% − gas window. Silurian = 0%; Ordovician = 0%; Cambrian = 100% |
| 7 | 8 | 0.13 | 422 | 1.08 | 19.90 | 278.67 | 28.25 | 0.77 | Ro = 0.77%; Ro + S = 0.78% − oil window. Silurian = 0%; Ordovician = 0%; Cambrian = 100% |
| 8 | 4 | 0.69 | 427 | 1.76 | 29.84 | 381.63 | 105.16 | 0.67 | Ro = 0.67%; Ro + S = 0.73% − oil window. Silurian = 0%; Ordovician = 100%; Cambrian = 0% |
| 10 | 4 | 0.13 | 437 | 0.30 | 4.50 | 339.66 | 275.61 | 0.77 | Ro = 0.77% − oil window; Ro + S = 0.85% − part in the condensate window. Silurian = 25%; Ordovician = 0%; Cambrian = 75% |
| 11 | 4 | 0.21 | 417 | 0.03 | 0.06 | 137. 06 | 287.87 | 1.33 | Ro = 1.33% − gas window; Ro − S = 1.02% − part in the condensate window. Silurian = 50%; Ordovician = 0%; Cambrian = 50% |
| Mean | 1.06 | 442 | 0.74 | 6.29 | 154.82 | 106.25 | 1.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwilosz, T.; Filar, B.; Miziołek, M. Use of Cluster Analysis to Group Organic Shale Gas Rocks by Hydrocarbon Generation Zones. Energies 2022, 15, 1464. https://doi.org/10.3390/en15041464
Kwilosz T, Filar B, Miziołek M. Use of Cluster Analysis to Group Organic Shale Gas Rocks by Hydrocarbon Generation Zones. Energies. 2022; 15(4):1464. https://doi.org/10.3390/en15041464
Chicago/Turabian StyleKwilosz, Tadeusz, Bogdan Filar, and Mariusz Miziołek. 2022. "Use of Cluster Analysis to Group Organic Shale Gas Rocks by Hydrocarbon Generation Zones" Energies 15, no. 4: 1464. https://doi.org/10.3390/en15041464
APA StyleKwilosz, T., Filar, B., & Miziołek, M. (2022). Use of Cluster Analysis to Group Organic Shale Gas Rocks by Hydrocarbon Generation Zones. Energies, 15(4), 1464. https://doi.org/10.3390/en15041464