Measuring and Analyzing Operational Efficiency and Returns to Scale in a Time Horizon: Assessment of China’s Electricity Generation & Transmission at Provincial Levels
Abstract
:1. Introduction
2. Previous Studies
3. Methods
- : the ith input of the jth DMU at the tth period,
- : the rth output of the jth DMU at the tth period,
- : the inefficiency score of the kth DMU at the tth period,
- : the data range adjustment on the ith input,
- : the data range adjustment on the rth output,
- : the intensity variable of the jth DMU at the tth period,
- : a prescribed very small number (e.g., 0.0001 in this research),
- : the dual variable (multiplier) of the ith input,
- : the dual variable (multiplier) of the rth output,
- : the dual variable that indicates an intercept of the supporting hyperplane.
3.1. Operational Efficiency
3.2. Durbin-Watson Statistic
3.3. K-Means Clustering and Group Classification
4. Returns to Scale
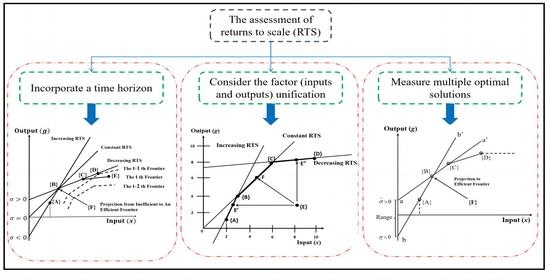
4.1. A Visual Description
4.2. A Supporting Hyperplane
4.3. Types of RTS and Chi-Square Test
4.4. Differences between Proposed Approach and Standard Approach
5. RTS Measurement under Multiple Solutions
6. Empirical Application
6.1. Data
6.2. OE Measures
6.3. RTS Measures
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 6, 429–444. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Goto, M. Environmental Assessment on Energy and Sustainability by Data Envelopment Analysis; John Wiley & Sons: London, UK, 2018; pp. 265–350. [Google Scholar]
- Banker, R.D. Estimating most productive scale size using data envelopment analysis. Eur. J. Oper. Res. 1984, 17, 35–44. [Google Scholar] [CrossRef]
- Chang, K.P.; Guh, Y.Y. Linear production functions and data envelopment analysis. Eur. J. Oper. Res. 1991, 52, 215–223. [Google Scholar] [CrossRef]
- Sueyoshi, T. DEA duality on Returns to Scale (RTS) in production and cost analyses. Manag. Sci. 1999, 45, 1593–1608. [Google Scholar] [CrossRef]
- International Energy Agency. Available online: https://www.iea.org/reports/world-energy-outlook-2019 (accessed on 22 December 2022).
- BP (British Petroleum 2022): BP Statistical Review of World Energy. Available online: http://www.bp.com/statisticalreview (accessed on 18 December 2022).
- Newbery, D. Electricity Liberalization in Britain and the Evolution of Market Design; Elsevier: Oxford, UK, 2006; pp. 109–143. [Google Scholar]
- Green, R. Electricity Deregulation in England and Wales; Springer: Boston, MA, USA, 2012; pp. 179–202. [Google Scholar]
- Taleb, M.; Khalid, R.; Ramli, R.; Ghasemi, M.; Ignatius, J. An integrated bi-objective data envelopment analysis model for measuring returns to scale. Eur. J. Oper. Res. 2022, 296, 967–979. [Google Scholar] [CrossRef]
- Mousavi, S.; Amirteimoori, A.; Kordrostami, S.; Vaez-Ghasemi, M. Non-radial two-stage network DEA model to estimate returns to scale. J. Model. Manag. 2021. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Liu, J.; Shuai, C. Is the photovoltaic poverty alleviation project the best way for the poor to escape poverty? A DEA and GRA analysis of different projects in rural China. Energy Policy 2020, 137, 111105. [Google Scholar] [CrossRef]
- Kuo, K.; Lu, W.; Le, M. Exploring the performance and competitiveness of Vietnam port industry using DEA. Asian J. Shipp. Logist. 2020, 36, 136–144. [Google Scholar] [CrossRef]
- Deng, F.; Xu, L.; Fang, Y.; Gong, Q.; Li, Z. PCA-DEA-Tobit regression assessment with carbon emission constraints of China’s logistics industry. J. Clean. Prod. 2020, 271, 122548. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Goto, M. The intermediate approach to sustainability enhancement and scale-related measures in environmental assessment. Eur. J. Oper. Res. 2019, 276, 744–756. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, H.; Gao, F.; Zhang, Q.; Zhang, J.; Zhou, Y. Multi-attribute decision making on reverse logistics based on DEA-TOPSIS. J. Clean. Prod. 2019, 214, 730–737. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, G.; Wang, C.; Wu, J. Modeling undesirable output with a DEA approach based on an exponential transformation. J. Clean. Prod. 2019, 236, 117717. [Google Scholar] [CrossRef]
- Taleb, M.; Khalid, R.; Ramli, R. Estimating the returns to scale of an integrated data envelopment analysis model: Efficiency assessment of a higher education institution. Arab. J. Basic Appl. Sci. 2019, 26, 144–152. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Beigi, Z.; Hougaard, J.; Gholami, K. Measurement of returns-to-scale using interval data envelopment analysis models. Comput. Ind. Eng. 2018, 117, 94–107. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Wang, M. Measuring scale efficiency and returns to scale on large commercial rooftop photovoltaic systems in California. Energy Econ. 2017, 65, 389–398. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Goto, M. Measurement of returns to scale on large photovoltaic power stations in the United States and Germany. Energy Econ. 2017, 64, 306–320. [Google Scholar] [CrossRef]
- Clercq, D.D.; Wen, Z.; Lu, X.; Caicedo, L.; Cao, X.; Fan, F. Determinants of efficiency in an industrial-scale anaerobic digestion food waste-to-biogas project in an Asian megacity based on data envelopment analysis and exploratory multivariate statistics. J. Clean. Prod. 2017, 168, 983–996. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y. Returns to damage under undesirable congestion and damages to return under desirable congestion measured by DEA environmental assessment with multiplier restriction. Energy Econ. 2016, 56, 288–309. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Goto, M. DEA radial measurement for environmental assessment. Appl. Energy 2014, 115, 502–513. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, H.; Yang, X.; Zhai, W.; Xia, Q.; Li, Y. An estimation of returns to scale of airport airsides under multiple optimal solutions in DEA. J. Air Transp. Manag. 2014, 40, 149–156. [Google Scholar] [CrossRef]
- Du, G.; Lin, W.; Zhang, B. The improved CCR returns to scale method in DEA. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC 2011), Dengfeng, China, 8–10 August 2011; pp. 3490–3494. [Google Scholar]
- Korhonen, P.J.; Soleimani-damaneh, M.; Wallenius, J. Ratio-based RTS determination in weight-restricted DEA models. Eur. J. Oper. Res. 2011, 215, 431–438. [Google Scholar] [CrossRef]
- Zhang, R.; Wei, Q.; Li, A.; Ren, L. Measuring efficiency and technology inequality of China’s electricity generation and transmission system: A new approach of network Data Envelopment Analysis prospect cross-efficiency models. Energy 2022, 246, 123274. [Google Scholar] [CrossRef]
- Li, W.; Ji, Z.; Dong, F. Global renewable energy power generation efficiency evaluation and influencing factors analysis. Sustain. Prod. Consum. 2022, 33, 438–453. [Google Scholar] [CrossRef]
- Xiao, Q.; Tian, Z.; Ren, F. Efficiency assessment of electricity generation in China using meta-frontier data envelopment analysis: Cross-regional comparison based on different electricity generation energy sources. Energy Strategy Rev. 2022, 39, 100767. [Google Scholar] [CrossRef]
- Eguchi, S.; Takayabu, H.; Lin, C. Sources of inefficient power generation by coal-fired thermal power plants in China. Renew. Sustain. Energy Rev. 2021, 138, 110562. [Google Scholar] [CrossRef]
- Fidanoski, F.; Simeonovski, K.; Cvetkoska, V. Energy Efficiency in OECD Countries. Energies 2021, 14, 1185. [Google Scholar] [CrossRef]
- Nakaishi, T.; Kagawa, S.; Takayabu, H.; Lin, C. Determinants of technical inefficiency in China’s coal-fired power plants and policy recommendations for CO2 mitigation. Environ. Sci. Pollut. Res. 2021, 28, 52064–52081. [Google Scholar] [CrossRef]
- Tavassoli, M.; Ketabi, S.; Ghandehari, M. Developing a network DEA model for sustainability analysis of Iran’s electricity distribution network. Electr. Power Energy Syst. 2020, 122, 106187. [Google Scholar] [CrossRef]
- Alizadeh, R.; Beiragh, R.; Soltanisehat, L.; Soltanzadeh, E.; Lund, P.D. Performance evaluation of complex electricity generation systems. Energy Econ. 2020, 91, 104894. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Qu, J.; Li, A.; Xie, C. Understanding the efficiency evolution for the Chinese provincial power industry. J. Clean. Prod. 2020, 277, 122371. [Google Scholar] [CrossRef]
- Cuadros, S.; Rodriguez, Y.; Contreras, J. Dynamic Data Envelopment Analysis Model Involving Undesirable Outputs in the Electricity Power Generation Sector. Energies 2020, 13, 6624. [Google Scholar] [CrossRef]
- Mahmoudi, R.; Emrouznejad, A.; Khosroshahi, H.; Khashei, M.; Parisa, R. Performance evaluation of thermal power plants considering CO2 emission. J. Clean. Prod. 2019, 223, 641–650. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Liang, Z.; Zhang, X.; Zhu, L. Efficiency evaluation of thermal power plants in China based on the weighted Russell directional distance method. J. Clean. Prod. 2019, 222, 573–583. [Google Scholar] [CrossRef]
- Lee, C. Decentralized allocation of emission permits by Nash data envelopment analysis in the coal-fired power market. J. Environ. Manag. 2019, 241, 353–362. [Google Scholar] [CrossRef]
- Halkos, G.E.; Polemis, M.L. The impact of economic growth on environmental efficiency of the electricity sector. J. Environ. Manag. 2018, 211, 334–346. [Google Scholar] [CrossRef]
- Sun, C.; Liu, X.; Li, A. Measuring unified efficiency of Chinese fossil fuel power plants. Energy Policy 2018, 123, 8–18. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Li, A.; Gao, Y. Sector sustainability on fossil fuel power plants across Chinese provinces. J. Clean. Prod. 2018, 187, 819–829. [Google Scholar] [CrossRef]
- Bi, G.; Shao, Y.; Song, W.; Yang, F.; Luo, Y. A performance evaluation of China’s coal-fired power generation with pollutant mitigation options. J. Clean. Prod. 2018, 171, 867–876. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, W.; Tian, J.; He, R.; Chen, L. Eco-efficiency assessment of coal-fired combined heat and power plants in Chinese eco-industrial parks. J. Clean. Prod. 2017, 168, 963–972. [Google Scholar] [CrossRef]
- Barros, C.P.; Wanke, P.; Dumbo, S.; Manso, J. Efficiency in Angolan hydro-electric power station. Renew. Sustain. Energy Rev. 2017, 78, 588–596. [Google Scholar] [CrossRef]
- Arabi, B.; Munisamy, S.; Emrouznejad, A.; Toloo, M.; Ghazizadeh, M. Eco-efficiency considering the issue of heterogeneity among power plants. Energy 2016, 111, 722–735. [Google Scholar] [CrossRef] [Green Version]
- Rutledge, D.N.; Barros, A.S. Durbin–Watson statistic as a morphological estimator of information content. Anal. Chim. Acta 2002, 454, 277–295. [Google Scholar] [CrossRef]
- Purohit, P.; Joshi, R. A New Efficient Approach towards K-means Clustering Algorithm. Int. J. Comput. Appl. 2013, 65, 7–10. [Google Scholar]
- Zhou, L.; Zhang, R.; Li, A. New concepts for bootstrap-based cross-efficiency and relative weight analysis and an application to China’s governance-finance-innovation-sustainability system. J. Clean. Prod. 2022, 379, 134549. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, G.; Zhang, J. The estimation of China’s provincial capital stock: 1952–2000. Econ. Res. J. 2004, 10, 10. [Google Scholar]
- China Electricity Council (2006–2019). Available online: https://bbs.pinggu.org/thread-10851578-1-1.html (accessed on 13 May 2021).
- Goto, M.; Sueyoshi, T. Sustainable development and convergence under energy sector transition in industrial nations: An application of DEA environment assessment. Socio-Econ. Plan. Sci. 2022, 101316. [Google Scholar] [CrossRef]






| Articles | Coverage | Addressing Problem of Multiple Solutions | Methods | Orientation | Time Horizon |
|---|---|---|---|---|---|
| Taleb et al. [10] | 39 airports, Spain, 2008 | Yes | Non-radial model | Non-oriented | No |
| Mousavi et al. [11] | 19 commercial branches, Iran, 2018 | Yes | Non-radial model | Non-oriented | No |
| Wang et al. [12] | 8 provinces, China, 2013–2017 | No | BCC | Input-oriented | No |
| Kuo et al. [13] | 53 ports, Vietnam, 2012–2016 | No | Context-dependent DEA | Output-oriented | No |
| Deng et al. [14] | 30 provinces, China, 2016 | No | Slack-Based Measure | Non-oriented | No |
| Sueyoshi and Goto [15] | 23 districts, Japan, 2014 | Yes | Intermediate approach | Output-oriented | No |
| Wang et al. [16] | 7 companies, China, 2017 | No | Slack-Based Measure | Non-oriented | No |
| Zhou et al. [17] | 38 sectors, China, 2010–2014 | No | BCC, CCR | Input-oriented | No |
| Taleb et al. [18] | 20 public universities, Malaysia, 2011 | No | Radial model | Output-oriented | No |
| Hatami-Marbini et al. [19] | 28 cities, China, 1983 | Yes | CCR | Input-oriented | No |
| Sueyoshi and Wang [20] | 855 PV systems, U.S., 2013 | Yes | Radial model | Input-oriented | No |
| Sueyoshi and Goto [21] | 160 PV power stations, U.S., Germany | Yes | Radial model | Input-oriented/Output-oriented | No |
| Clercq et al. [22] | 15 cities, Asia, 2015–2017 | No | BCC | Input-oriented | No |
| Sueyoshi and Yuan [23] | 30 provinces, China, 2005–2012 | Yes | Radial model | Output-oriented | No |
| Sueyoshi and Goto [24] | 31 chemical and pharmaceutical firms, Japan, 2007–2010 | Yes | Radial model | Output-oriented | No |
| Zhang et al. [25] | 37 airport airsides, China, 2009 | Yes | BCC, CCR | Output-oriented | No |
| Du et al. [26] | 15 companies, Japan, 1995 | Yes | CCR | Input-oriented | No |
| Korhonen et al. [27] | 80 secondary schools, Iran, 1994 | Yes | BCC, CCR | Input-oriented | No |
| Articles | Coverage | Inputs a | Outputs b | Methods c | Other Assisting Methods | RTS |
|---|---|---|---|---|---|---|
| Zhang et al. [28] | 30 provinces, China, 2010–2019 | K, coal, generation investment, grid investment | EL, electricity sold, electricity loss | Network DEA model | Mann-Whitney U test | No |
| Li et al. [29] | 36 countries, 2009–2018 | K | EL | Super-efficiency DEA | Random forest regression | No |
| Xiao et al. [30] | 31 provinces, China, 2013–2017 | K, L | EL, CO2 | Epsilon-based measure | Technology gap ratio | No |
| Eguchi et al. [31] | Power plants, China, 2009–2011 | Coal, capital | EL | Slack-Based Measure | No | No |
| Fidanoski et al. [32] | 30 countries, 2001–2018 | K, primary energy trade dependence, primary energy from renewables, electricity from renewables, R&D expenditure rate, urbanization rate | Primary energy intensity, electricity intensity, electricity loss ratio, CO2 | Output-oriented BCC model | No | No |
| Nakaishi et al. [33] | 28 provinces, China, 2014 | K, coal, electricity used | EL | Input-oriented radial model | Tobit regression analysis | No |
| Tavassoli et al. [34] | 16 electricity distribution networks, Iran, 2017 | L, oil, natural gas, purchases from neighbor, internal consumption, network length | EL, electricity transmission, sales volume, service area, loss electricity | Network DEA model | Sensitivity analysis, correlation coefficient | No |
| Alizadeh et al. [35] | 16 regional electrical companies, Iran, 2017–2019 | K, L, fuel | Sold energy, number of customers, distribution transformer, transmission line length | Dynamic DEA model | No | No |
| Sueyoshi et al. [36] | 30 provinces, China, 2009–2015 | K, L, energy | EL, CO2 | Radial model | Discriminant Analysis | No |
| Cuadros et al. [37] | 24 countries, 2000–2016 | Gross domestic product per capita, K | EL, CO2 | Dynamic slack-based DEA model | Moran’s Index | No |
| Mahmoudi et al. [38] | 24 thermal power plants, Iran, 2018 | K, L, C, fuel, total hours of operation, internal consumption | EL, CO2, revenue | Game DEA model | Principal Component Analysis, Shannon Entropy method | No |
| Xie et al. [39] | 30 provinces, China, 2012–2014 | L, asset, energy | Generation capacity, CO2 | Directional distance function | Mann-Whitney U test, Kolmogorov-Smirnov test | No |
| Lee [40] | 33 coal-burning power plants, China, 2013 | K, coal, operating hours | EL, CO2 | Nash DEA model | Wilcoxon matched-pairs signed-rank test | No |
| Halkos and Polemis [41] | 789 electric utilities, U.S., 2000–2012 | C, energy transmission | Utilization of net capacity, CO2, SO2, NOx | DEA window model | Fixed-effects panel data model | No |
| Sun et al. [42] | 30 provinces, China, 2005–2015 | K, L, energy | EL, CO2 | Intermediate approach | Mann-Whitney U test | No |
| Sueyoshi et al. [43] | 30 provinces, China, 2015 | K, L, energy | EL, CO2 | Radial model, non-radial model, intermediate approach | Mann-Whitney U test | No |
| Bi et al. [44] | 28 coal-fired power plants, China, 2010 | K, L, coal | EL, SO2 | Two-stage DEA model | No | No |
| Guo et al. [45] | 44 coal-fired combined heat and power plants, China, 2012 | C, coal, freshwater, capital depreciation | EL, heat, GHG emissions | Slack-Based Measure | Sensitivity analysis | No |
| Barros et al. [46] | 10 hydro-electric power stations, Angola, 2004–2014 | K, C | EL | Dynamic RAM model | Simplex regression | No |
| Arabi et al. [47] | 52 power plants, Iran, 2003–2010 | C, fuel, capital, depreciation | EL, SO2, operational availability, deviation charges | Non-radial model | Malmquist Luenberger indices | No |
| Indicators | Inputs | Outputs | |||
|---|---|---|---|---|---|
| Installed Capacity | Raw Coal | Grid Investment | Electricity | Equivalent User | |
| 103 kW | 103 tons | 109 RMB | 109 kWh | Household | |
| Average | 42,034.94 | 54,897.81 | 21.69 | 136.77 | 168,651.10 |
| Standard Deviation | 29,084.67 | 46,441.00 | 18.26 | 107.07 | 194,549.90 |
| Minimum | 2580.00 | 360.00 | 1.45 | 7.44 | 4674.00 |
| Maximum | 140,440.00 | 267,920.00 | 130.90 | 611.80 | 1,488,872.00 |
| Groups | Provinces | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 (low efficiency) | Anhui | 0.75 | 0.72 | 0.59 | 0.56 | 0.62 | 0.69 | 0.75 | 0.81 | 0.74 | 0.70 | 0.64 | 0.65 | 0.66 | 0.67 | 0.68 |
| Chongqing | 0.67 | 0.62 | 0.83 | 0.68 | 0.63 | 0.63 | 0.60 | 0.82 | 0.83 | 0.80 | 0.84 | 0.91 | 0.91 | 0.96 | 0.76 | |
| Gansu | 0.88 | 0.86 | 0.83 | 0.76 | 0.65 | 0.63 | 0.72 | 0.70 | 0.73 | 0.69 | 0.63 | 0.65 | 0.70 | 0.81 | 0.73 | |
| Guizhou | 0.94 | 0.89 | 0.88 | 0.78 | 0.78 | 0.72 | 0.76 | 0.75 | 0.82 | 0.81 | 0.78 | 0.74 | 0.72 | 0.79 | 0.80 | |
| Heilongjiang | 0.98 | 0.78 | 0.69 | 0.65 | 0.68 | 0.72 | 0.76 | 0.73 | 0.84 | 0.87 | 0.73 | 0.72 | 0.81 | 1.00 | 0.78 | |
| Hubei | 0.68 | 0.65 | 0.64 | 0.60 | 0.65 | 0.64 | 0.65 | 0.72 | 0.62 | 0.66 | 0.79 | 0.87 | 0.82 | 0.94 | 0.71 | |
| Hunan | 0.67 | 0.63 | 0.55 | 0.55 | 0.61 | 0.65 | 0.72 | 0.78 | 0.92 | 0.87 | 0.84 | 0.84 | 0.85 | 0.96 | 0.75 | |
| Inner Mongolia | 0.88 | 0.89 | 0.85 | 0.87 | 0.98 | 0.68 | 0.49 | 0.57 | 0.63 | 0.61 | 0.55 | 0.55 | 0.60 | 0.70 | 0.70 | |
| Jiangxi | 0.66 | 0.60 | 0.70 | 0.68 | 0.72 | 0.80 | 0.87 | 0.88 | 0.90 | 0.85 | 0.81 | 0.77 | 0.90 | 0.88 | 0.79 | |
| Jilin | 0.74 | 0.83 | 0.77 | 0.67 | 0.70 | 0.62 | 0.74 | 0.96 | 0.81 | 0.88 | 0.79 | 0.79 | 0.83 | 1.00 | 0.80 | |
| Ningxia | 0.88 | 0.96 | 0.77 | 0.78 | 0.75 | 0.82 | 0.80 | 0.78 | 0.73 | 0.58 | 0.51 | 0.64 | 0.72 | 0.84 | 0.75 | |
| Shaanxi | 0.74 | 0.70 | 0.62 | 0.50 | 0.62 | 0.63 | 0.64 | 0.65 | 0.71 | 0.68 | 0.67 | 0.67 | 0.64 | 0.65 | 0.65 | |
| Shanxi | 0.70 | 0.68 | 0.64 | 0.57 | 0.60 | 0.79 | 0.78 | 0.96 | 0.68 | 0.55 | 0.51 | 0.63 | 0.82 | 0.80 | 0.69 | |
| Sichuan | 0.80 | 0.71 | 0.71 | 0.60 | 0.65 | 0.69 | 0.68 | 0.70 | 0.67 | 0.74 | 0.81 | 0.87 | 0.87 | 0.99 | 0.75 | |
| Tianjin | 0.86 | 0.73 | 0.68 | 0.58 | 0.62 | 0.66 | 0.67 | 0.83 | 0.75 | 0.67 | 0.71 | 0.69 | 0.80 | 0.75 | 0.71 | |
| Xinjiang | 0.92 | 0.72 | 0.84 | 0.62 | 0.52 | 0.51 | 0.54 | 0.58 | 0.64 | 0.62 | 0.56 | 0.65 | 0.57 | 0.56 | 0.63 | |
| Group average | 0.80 | 0.75 | 0.72 | 0.65 | 0.67 | 0.68 | 0.70 | 0.76 | 0.75 | 0.72 | 0.70 | 0.73 | 0.76 | 0.83 | 0.73 | |
| Group 2 (high efficiency) | Beijing | 1.00 | 1.00 | 0.95 | 0.96 | 0.99 | 1.00 | 1.00 | 1.00 | 0.91 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 |
| Fujian | 0.65 | 0.64 | 0.73 | 0.77 | 0.75 | 0.81 | 0.83 | 0.82 | 0.78 | 0.87 | 1.00 | 0.86 | 0.89 | 0.94 | 0.81 | |
| Guangdong | 0.93 | 0.95 | 0.96 | 0.96 | 0.98 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | |
| Guangxi | 0.94 | 0.88 | 0.91 | 0.76 | 0.79 | 0.85 | 0.86 | 0.86 | 0.93 | 0.95 | 0.84 | 0.85 | 0.92 | 0.87 | 0.87 | |
| Hainan | 1.00 | 0.92 | 1.00 | 0.88 | 0.80 | 0.83 | 0.84 | 0.88 | 0.97 | 0.87 | 0.83 | 0.89 | 0.84 | 0.84 | 0.88 | |
| Hebei | 1.00 | 0.98 | 0.97 | 0.95 | 0.98 | 1.00 | 1.00 | 0.97 | 1.00 | 0.95 | 0.92 | 0.95 | 0.94 | 0.97 | 0.97 | |
| Henan | 0.69 | 0.73 | 0.76 | 0.77 | 0.83 | 0.87 | 0.87 | 1.00 | 0.85 | 0.79 | 0.78 | 0.79 | 0.82 | 0.81 | 0.81 | |
| Jiangsu | 0.79 | 0.84 | 0.89 | 0.90 | 0.94 | 0.96 | 0.97 | 1.00 | 1.00 | 0.99 | 0.99 | 0.98 | 0.99 | 1.00 | 0.95 | |
| Liaoning | 0.94 | 0.87 | 0.88 | 0.81 | 0.80 | 0.83 | 0.81 | 0.94 | 0.82 | 0.84 | 0.82 | 0.83 | 0.84 | 0.88 | 0.85 | |
| Qinghai | 1.00 | 0.91 | 0.90 | 0.85 | 0.90 | 0.87 | 0.83 | 0.92 | 0.92 | 0.87 | 0.79 | 0.88 | 0.98 | 0.84 | 0.89 | |
| Shandong | 0.73 | 0.73 | 0.75 | 0.75 | 0.89 | 0.94 | 0.93 | 0.94 | 0.86 | 0.79 | 0.75 | 0.74 | 0.79 | 0.81 | 0.81 | |
| Shanghai | 0.81 | 0.87 | 0.85 | 0.82 | 0.91 | 0.98 | 0.95 | 0.98 | 0.84 | 0.83 | 0.86 | 0.90 | 0.88 | 0.92 | 0.89 | |
| Yunnan | 0.73 | 0.72 | 0.80 | 0.71 | 0.76 | 0.91 | 0.83 | 0.87 | 0.88 | 0.85 | 0.93 | 0.98 | 0.95 | 1.00 | 0.85 | |
| Zhejiang | 0.71 | 0.75 | 0.77 | 0.78 | 0.86 | 0.89 | 0.93 | 0.93 | 0.88 | 0.88 | 0.89 | 0.89 | 0.90 | 0.97 | 0.86 | |
| Group average | 0.85 | 0.84 | 0.87 | 0.83 | 0.87 | 0.91 | 0.90 | 0.94 | 0.90 | 0.89 | 0.89 | 0.89 | 0.91 | 0.92 | 0.89 | |
| China’s average | 0.82 | 0.79 | 0.79 | 0.74 | 0.76 | 0.79 | 0.79 | 0.84 | 0.82 | 0.80 | 0.79 | 0.81 | 0.83 | 0.87 | 0.80 | |
| Indicators | Group 1 (Low Efficiency) | Group 2 (High Efficiency) |
|---|---|---|
| Maximum | 1.00 | 1.00 |
| Minimum | 0.49 | 0.64 |
| Average | 0.73 | 0.89 |
| Standard Deviation | 0.05 | 0.06 |
| Number of efficient observations | 2 | 30 |
| Groups | Provinces | d | Groups | Provinces | d |
|---|---|---|---|---|---|
| Group 1 | Anhui | 0.007 | Group 2 | Beijing | 0.001 |
| Chongqing | 0.015 | Fujian | 0.007 | ||
| Gansu | 0.006 | Guangdong | 0.000 | ||
| Guizhou | 0.003 | Guangxi | 0.006 | ||
| Heilongjiang | 0.016 | Hainan | 0.005 | ||
| Hubei | 0.009 | Hebei | 0.001 | ||
| Hunan | 0.007 | Henan | 0.006 | ||
| Inner Mongolia | 0.023 | Jiangsu | 0.001 | ||
| Jiangxi | 0.006 | Liaoning | 0.004 | ||
| Jilin | 0.017 | Qinghai | 0.006 | ||
| Ningxia | 0.015 | Shandong | 0.004 | ||
| Shaanxi | 0.007 | Shanghai | 0.004 | ||
| Shanxi | 0.032 | Yunnan | 0.006 | ||
| Sichuan | 0.007 | Zhejiang | 0.002 | ||
| Tianjin | 0.012 | ||||
| Xinjiang | 0.026 |
| Yeas | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | |||||||
| Provinces | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound |
| Beijing | 0.015 | −0.246 | 0.017 | −0.300 | −0.226 | −0.226 | −0.216 | −0.216 | −0.205 | −0.205 | 0.375 | −0.203 | 0.372 | −0.174 |
| Tianjin | −0.099 | −0.099 | −0.206 | −0.206 | −0.042 | −0.042 | −0.033 | −0.033 | 0.357 | 0.357 | 0.344 | 0.344 | 0.334 | 0.334 |
| Hebei | 0.036 | −0.045 | 0.058 | 0.058 | 0.055 | 0.055 | 0.047 | 0.047 | 0.043 | 0.043 | 0.135 | 0.039 | 0.089 | 0.078 |
| Shanxi | −0.039 | −0.039 | 0.001 | 0.001 | 0.002 | 0.002 | 0.002 | 0.002 | 0.030 | 0.030 | −0.051 | −0.051 | −0.048 | −0.048 |
| Inner Mongolia | −0.093 | −0.093 | 0.050 | 0.050 | 0.043 | 0.043 | 0.041 | 0.041 | 0.040 | 0.040 | 0.030 | 0.030 | −0.033 | −0.033 |
| Liaoning | −0.043 | −0.043 | 0.044 | 0.044 | 0.042 | 0.042 | 0.072 | 0.072 | 0.059 | 0.059 | 0.116 | 0.116 | 0.115 | 0.115 |
| Jilin | −0.093 | −0.093 | −0.164 | −0.164 | −0.117 | −0.117 | −0.064 | −0.064 | −0.114 | −0.114 | −0.043 | −0.043 | −0.074 | −0.074 |
| Heilongjiang | −0.169 | −0.169 | −0.126 | −0.126 | −0.060 | −0.060 | −0.050 | −0.050 | −0.048 | −0.048 | −0.051 | −0.051 | −0.048 | −0.048 |
| Shanghai | 0.004 | 0.004 | 0.004 | 0.004 | 0.003 | 0.003 | 0.095 | 0.095 | 0.003 | 0.003 | −0.037 | −0.037 | −0.029 | −0.029 |
| Jiangsu | 0.102 | 0.102 | 0.091 | 0.091 | 0.090 | 0.090 | 0.085 | 0.085 | 0.075 | 0.075 | 0.068 | 0.068 | 0.063 | 0.063 |
| Zhejiang | 0.112 | 0.112 | 0.107 | 0.107 | 0.101 | 0.101 | 0.095 | 0.095 | 0.088 | 0.088 | 0.081 | 0.081 | 0.075 | 0.075 |
| Anhui | −0.056 | −0.056 | −0.047 | −0.047 | −0.036 | −0.036 | 0.003 | 0.003 | 0.003 | 0.003 | −0.032 | −0.032 | −0.029 | −0.029 |
| Fujian | −0.023 | −0.023 | −0.019 | −0.019 | −0.021 | −0.021 | −0.018 | −0.018 | 0.013 | 0.013 | −0.014 | −0.014 | −0.025 | −0.025 |
| Jiangxi | −0.083 | −0.083 | −0.059 | −0.059 | −0.065 | −0.065 | −0.049 | −0.049 | −0.044 | −0.044 | −0.046 | −0.046 | −0.041 | −0.041 |
| Shandong | 0.024 | 0.024 | 0.041 | 0.041 | 0.069 | 0.069 | 0.091 | 0.091 | 0.116 | 0.116 | 0.100 | 0.100 | 0.065 | 0.065 |
| Henan | 0.002 | 0.002 | 0.029 | 0.029 | 0.048 | 0.048 | 0.080 | 0.080 | 0.072 | 0.072 | 0.081 | 0.081 | 0.078 | 0.078 |
| Hubei | −0.023 | −0.023 | −0.020 | −0.020 | −0.018 | −0.018 | −0.016 | −0.016 | −0.015 | −0.015 | −0.013 | −0.013 | 0.032 | 0.032 |
| Hunan | −0.025 | −0.025 | −0.021 | −0.021 | 0.015 | 0.015 | 0.201 | 0.201 | 0.136 | 0.136 | 0.123 | 0.123 | −0.018 | −0.018 |
| Guangdong | 0.079 | 0.079 | 0.075 | 0.075 | 0.072 | 0.072 | 0.080 | 0.080 | 0.071 | 0.071 | 0.061 | 0.061 | 0.112 | 0.049 |
| Guangxi | −0.040 | −0.040 | −0.030 | −0.030 | −0.027 | −0.027 | −0.024 | −0.024 | −0.022 | −0.022 | −0.021 | −0.021 | −0.035 | −0.035 |
| Hainan | −0.446 | −1.000 | −0.417 | −0.417 | −0.287 | −1.000 | −0.352 | −0.352 | −0.263 | −0.263 | −0.175 | −0.175 | −0.309 | −0.309 |
| Chongqing | −0.084 | −0.084 | −0.071 | −0.071 | −0.064 | −0.064 | −0.050 | −0.050 | 0.004 | 0.004 | 0.008 | 0.008 | −0.050 | −0.050 |
| Sichuan | −0.019 | −0.019 | −0.017 | −0.017 | 0.014 | 0.014 | 0.012 | 0.012 | 0.127 | 0.127 | 0.113 | 0.113 | 0.044 | 0.044 |
| Guizhou | −0.099 | −0.099 | −0.078 | −0.078 | −0.074 | −0.074 | −0.023 | −0.023 | −0.016 | −0.016 | −0.015 | −0.015 | −0.014 | −0.014 |
| Yunnan | −0.037 | −0.037 | −0.029 | −0.029 | −0.020 | −0.020 | 0.014 | 0.014 | 0.012 | 0.012 | 0.011 | 0.011 | 0.026 | 0.026 |
| Shaanxi | −0.065 | −0.065 | −0.055 | −0.055 | −0.037 | −0.037 | 0.003 | 0.003 | −0.037 | −0.037 | 0.003 | 0.003 | 0.001 | 0.001 |
| Gansu | −0.069 | −0.069 | −0.059 | −0.059 | −0.053 | −0.053 | −0.031 | −0.031 | −0.031 | −0.031 | −0.019 | −0.019 | −0.033 | −0.033 |
| Qinghai | −0.105 | −0.815 | −0.112 | −0.112 | −0.101 | −0.101 | −0.139 | −0.139 | −0.108 | −0.108 | −0.089 | −0.089 | −0.098 | −0.098 |
| Ningxia | −0.119 | −0.119 | −0.118 | −0.118 | −0.093 | −0.093 | −0.082 | −0.082 | −0.064 | −0.064 | −0.102 | −0.102 | −0.078 | −0.078 |
| Xinjiang | −0.328 | −0.328 | −0.114 | −0.114 | −0.196 | −0.196 | −0.073 | −0.073 | −0.052 | −0.052 | −0.039 | −0.039 | −0.029 | −0.029 |
| Years | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |||||||
| Provinces | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound | Upper bound | Lower bound |
| Beijing | 0.427 | −0.208 | 0.334 | 0.334 | −0.248 | −0.248 | −0.008 | −0.331 | −0.182 | −1.000 | −0.009 | −0.009 | 0.844 | −1.000 |
| Tianjin | −0.060 | −0.060 | −0.046 | −0.046 | 0.257 | 0.257 | −0.043 | −0.043 | −0.041 | −0.041 | −0.044 | −0.044 | −0.039 | −0.039 |
| Hebei | 0.077 | 0.077 | 0.373 | −0.036 | 0.078 | 0.078 | 0.075 | 0.075 | 0.065 | 0.065 | 0.060 | 0.060 | 0.057 | 0.057 |
| Shanxi | 0.147 | 0.147 | −0.041 | −0.041 | −0.010 | −0.010 | −0.009 | −0.009 | 0.023 | 0.023 | 0.027 | 0.027 | 0.024 | 0.024 |
| Inner Mongolia | 0.022 | 0.022 | 0.024 | 0.024 | 0.024 | 0.024 | 0.020 | 0.020 | 0.017 | 0.017 | 0.016 | 0.016 | 0.364 | 0.364 |
| Liaoning | 0.105 | 0.105 | 0.105 | 0.105 | −0.020 | −0.020 | −0.020 | −0.020 | −0.019 | −0.019 | 0.026 | 0.026 | −0.018 | −0.018 |
| Jilin | −0.075 | −0.075 | −0.071 | −0.071 | −0.091 | −0.091 | −0.073 | −0.073 | −0.063 | −0.063 | −0.069 | −0.069 | 0.087 | −0.157 |
| Heilongjiang | −0.047 | −0.047 | −0.086 | −0.086 | −0.085 | −0.085 | −0.036 | −0.036 | −0.034 | −0.034 | −0.058 | −0.058 | 0.363 | −0.326 |
| Shanghai | −0.037 | −0.037 | 0.170 | 0.170 | 0.187 | 0.187 | 0.156 | 0.156 | 0.131 | 0.131 | 0.169 | 0.169 | 0.014 | 0.014 |
| Jiangsu | 1.000 | 0.013 | 0.264 | 0.048 | 0.103 | 0.103 | 0.236 | 0.236 | 0.215 | 0.215 | 0.238 | 0.238 | 0.979 | 0.035 |
| Zhejiang | 0.070 | 0.070 | 0.073 | 0.073 | 0.072 | 0.072 | 0.058 | 0.058 | 0.055 | 0.055 | 0.050 | 0.050 | 0.048 | 0.048 |
| Anhui | −0.024 | −0.024 | −0.026 | −0.026 | −0.019 | −0.019 | 0.025 | 0.025 | 0.023 | 0.023 | 0.021 | 0.021 | 0.020 | 0.020 |
| Fujian | −0.013 | −0.013 | 0.010 | 0.010 | −0.022 | −0.022 | 0.872 | −0.311 | 0.029 | 0.029 | 0.027 | 0.027 | −0.019 | −0.019 |
| Jiangxi | −0.041 | −0.041 | −0.039 | −0.039 | −0.035 | −0.035 | −0.030 | −0.030 | −0.027 | −0.027 | −0.029 | −0.029 | −0.027 | −0.027 |
| Shandong | 0.061 | 0.061 | 0.063 | 0.063 | 0.063 | 0.063 | 0.058 | 0.058 | 0.185 | 0.185 | 0.177 | 0.177 | 0.170 | 0.170 |
| Henan | 0.844 | −0.025 | 0.076 | 0.076 | 0.076 | 0.076 | 0.072 | 0.072 | 0.067 | 0.067 | 0.057 | 0.057 | 0.081 | 0.081 |
| Hubei | 0.155 | 0.155 | 0.136 | 0.136 | 0.165 | 0.165 | −0.041 | −0.041 | −0.040 | −0.040 | −0.036 | −0.036 | 0.015 | 0.015 |
| Hunan | −0.029 | −0.029 | −0.031 | −0.031 | −0.029 | −0.029 | −0.029 | −0.029 | 0.155 | 0.155 | 0.050 | 0.050 | −0.026 | −0.026 |
| Guangdong | 0.052 | 0.052 | 0.164 | 0.037 | 0.045 | 0.045 | 0.044 | 0.044 | 0.643 | 0.004 | 0.664 | 0.129 | 1.000 | 0.113 |
| Guangxi | −0.019 | −0.019 | −0.034 | −0.034 | −0.034 | −0.034 | −0.030 | −0.030 | −0.071 | −0.071 | −0.027 | −0.027 | 0.011 | 0.011 |
| Hainan | −0.162 | −0.162 | −0.159 | −0.159 | −0.155 | −0.155 | −0.182 | −0.182 | −0.179 | −0.179 | −0.159 | −0.159 | −0.151 | −0.151 |
| Chongqing | −0.047 | −0.047 | −0.045 | −0.045 | −0.043 | −0.043 | −0.048 | −0.048 | −0.041 | −0.041 | −0.037 | −0.037 | −0.037 | −0.037 |
| Sichuan | 0.043 | 0.043 | 0.043 | 0.043 | 0.253 | 0.253 | 0.772 | 0.772 | 0.723 | 0.723 | 0.649 | 0.649 | −0.059 | −0.059 |
| Guizhou | −0.013 | −0.013 | −0.013 | −0.013 | −0.024 | −0.024 | −0.022 | −0.022 | −0.019 | −0.019 | 0.027 | 0.027 | −0.018 | −0.018 |
| Yunnan | 0.010 | 0.010 | −0.013 | −0.013 | 0.046 | 0.046 | 0.704 | 0.704 | 0.656 | 0.656 | 0.203 | 0.203 | 0.621 | −0.062 |
| Shaanxi | 0.003 | 0.003 | −0.032 | −0.032 | −0.024 | −0.024 | −0.016 | −0.016 | −0.014 | −0.014 | −0.013 | −0.013 | −0.012 | −0.012 |
| Gansu | −0.031 | −0.031 | −0.034 | −0.034 | −0.064 | −0.064 | −0.056 | −0.056 | −0.057 | −0.057 | −0.037 | −0.037 | −0.058 | −0.058 |
| Qinghai | −0.035 | −0.035 | −0.076 | −0.076 | −0.079 | −0.079 | −0.071 | −0.071 | −0.073 | −0.073 | −0.208 | −0.208 | −0.184 | −0.184 |
| Ningxia | −0.070 | −0.070 | −0.041 | −0.041 | −0.021 | −0.021 | −0.019 | −0.019 | −0.033 | −0.033 | −0.055 | −0.055 | 0.068 | 0.068 |
| Xinjiang | −0.013 | −0.013 | −0.057 | −0.057 | −0.050 | −0.050 | −0.044 | −0.044 | −0.050 | −0.050 | −0.039 | −0.039 | −0.036 | −0.036 |
| Groups | Provinces | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 | Anhui | I | I | I | D | D | I | I | I | I | I | D | D | D | D |
| Chongqing | I | I | I | I | D | D | I | I | I | I | I | I | I | I | |
| Gansu | I | I | I | I | I | I | I | I | I | I | I | I | I | I | |
| Guizhou | I | I | I | I | I | I | I | I | I | I | I | I | D | I | |
| Heilongjiang | I | I | I | I | I | I | I | I | I | I | I | I | I | C | |
| Hubei | I | I | I | I | I | I | D | D | D | D | I | I | I | D | |
| Hunan | I | I | D | D | D | D | I | I | I | I | I | D | D | I | |
| Inner Mongolia | I | D | D | D | D | D | I | D | D | D | D | D | D | D | |
| Jiangxi | I | I | I | I | I | I | I | I | I | I | I | I | I | I | |
| Jilin | I | I | I | I | I | I | I | I | I | I | I | I | I | C | |
| Ningxia | I | I | I | I | I | I | I | I | I | I | I | I | I | D | |
| Shaanxi | I | I | I | D | I | D | D | D | I | I | I | I | I | I | |
| Shanxi | I | D | D | D | D | I | I | D | I | I | I | D | D | D | |
| Sichuan | I | I | D | D | D | D | D | D | D | D | D | D | D | I | |
| Tianjin | I | I | I | I | D | D | D | I | I | D | I | I | I | I | |
| Xinjiang | I | I | I | I | I | I | I | I | I | I | I | I | I | I | |
| Aggregation | Increasing RTS | 16 | 14 | 12 | 10 | 9 | 10 | 12 | 11 | 13 | 12 | 13 | 11 | 10 | 9 |
| Constant RTS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | |
| Decreasing RTS | 0 | 2 | 4 | 6 | 7 | 6 | 4 | 5 | 3 | 4 | 3 | 5 | 6 | 5 | |
| Group 2 | Beijing | C | C | I | I | I | C | C | C | D | I | I | I | I | C |
| Fujian | I | I | I | I | D | I | I | I | D | I | C | D | D | I | |
| Guangdong | D | D | D | D | D | D | D | D | D | D | D | D | D | D | |
| Guangxi | I | I | I | I | I | I | I | I | I | I | I | I | I | D | |
| Hainan | I | I | I | I | I | I | I | I | I | I | I | I | I | I | |
| Hebei | C | D | D | D | D | D | D | D | C | D | D | D | D | D | |
| Henan | D | D | D | D | D | D | D | C | D | D | D | D | D | D | |
| Jiangsu | D | D | D | D | D | D | D | D | D | D | D | D | D | D | |
| Liaoning | I | D | D | D | D | D | D | D | D | I | I | I | D | I | |
| Qinghai | I | I | I | I | I | I | I | I | I | I | I | I | I | I | |
| Shandong | D | D | D | D | D | D | D | D | D | D | D | D | D | D | |
| Shanghai | D | D | D | D | D | I | I | I | D | D | D | D | D | D | |
| Yunnan | I | I | I | D | D | D | D | D | I | D | D | D | D | C | |
| Zhejiang | D | D | D | D | D | D | D | D | D | D | D | D | D | D | |
| Aggregation | Increasing RTS | 6 | 5 | 6 | 5 | 4 | 5 | 5 | 5 | 4 | 6 | 5 | 5 | 4 | 4 |
| Constant RTS | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 2 | 1 | 0 | 1 | 0 | 0 | 2 | |
| Decreasing RTS | 6 | 8 | 8 | 9 | 10 | 8 | 8 | 7 | 9 | 8 | 8 | 9 | 10 | 8 |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | overall |
|---|---|---|---|---|---|---|---|---|
| χ2 | 12.468 *** | 8.769 ** | 3.214 * | 2.143 | 2.330 | 2.832 | 5.105 * | 59.890 *** |
| p-value | 0.002 | 0.012 | 0.073 | 0.143 | 0.127 | 0.243 | 0.078 | 0.000 |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
| χ2 | 4.470 | 8.670 ** | 3.214 * | 6.725 ** | 3.274 * | 3.453 * | 2.493 | |
| p-value | 0.107 | 0.013 | 0.073 | 0.035 | 0.070 | 0.063 | 0.287 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sueyoshi, T.; Zhang, R.; Li, A. Measuring and Analyzing Operational Efficiency and Returns to Scale in a Time Horizon: Assessment of China’s Electricity Generation & Transmission at Provincial Levels. Energies 2023, 16, 1006. https://doi.org/10.3390/en16021006
Sueyoshi T, Zhang R, Li A. Measuring and Analyzing Operational Efficiency and Returns to Scale in a Time Horizon: Assessment of China’s Electricity Generation & Transmission at Provincial Levels. Energies. 2023; 16(2):1006. https://doi.org/10.3390/en16021006
Chicago/Turabian StyleSueyoshi, Toshiyuki, Ruchuan Zhang, and Aijun Li. 2023. "Measuring and Analyzing Operational Efficiency and Returns to Scale in a Time Horizon: Assessment of China’s Electricity Generation & Transmission at Provincial Levels" Energies 16, no. 2: 1006. https://doi.org/10.3390/en16021006
APA StyleSueyoshi, T., Zhang, R., & Li, A. (2023). Measuring and Analyzing Operational Efficiency and Returns to Scale in a Time Horizon: Assessment of China’s Electricity Generation & Transmission at Provincial Levels. Energies, 16(2), 1006. https://doi.org/10.3390/en16021006