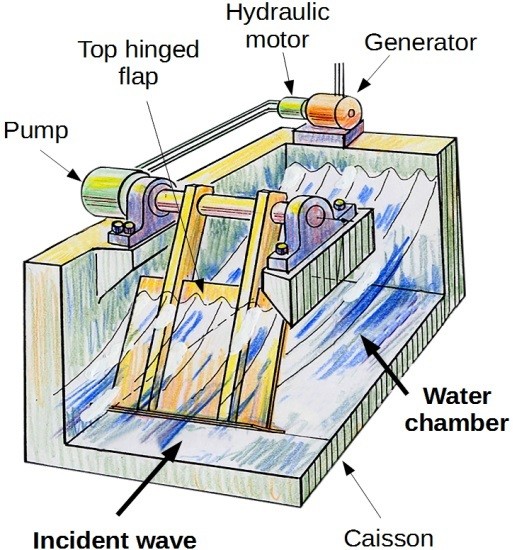
Study on the Performance of the “Pendulor” Wave Energy Converter in an Array Configuration
Abstract
:1. Introduction
2. Formulation of the Problem
2.1. Governing Equation
2.2. Governing Equation in Frequency Domain (Linear System)
2.3. Governing Equation in Time Domain
2.3.1. Radiation Moment Function in Sea Side
2.3.2. Radiation Moment Function in Chamber Side
2.4. System Identification
2.4.1. Sea Side System Identification
2.4.2. Chamber Side System Identification
3. Characteristics of the Plant
3.1. The Case of Regular Waves
3.1.1. Linear Damping
3.1.2. Coulomb Damping
3.2. The Case of Irregular Waves
3.3. Influence of the Chamber Length
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations and Notations
| FDI | frequency domain identification |
| OWC | oscillation water column |
| OSWC | oscillating Surge Wave Converter |
| PTO | power take off system |
| SSM | state space models |
| TDI | time domain identification |
| TF | transfer function |
imaginary part of the radiation impedance | |
frequency dependent radiation moment (real part of the radiation impedance) | |
| b | width of the flap |
group velocity | |
capture factor | |
| d | Chamber length (length from flap tp back wall of the flap) |
non-dimensional chamber length | |
effective chamber length (when plant tuned at T = 12 s) | |
buoyancy moment | |
drag moment on the flap | |
excitation moment | |
hydro dynamic and static moments applying on the flap | |
restoring moment due to mass of the flap | |
external mechanical torque on the flap | |
radiation moment | |
| g | acceleration due to gravity |
| H | amplitude of the incoming wave |
significant wave height | |
| h | water depth of the chamber |
moment of inertia of the flap | |
| I | frequency dependent added inertia |
| k | hydrostatic restoring coefficient |
root of the dispersion relationship | |
restoring coefficient of PTO | |
restoring coefficient due to mass of the flap | |
non-dimensional wave length | |
| l | free surface of water to hinged point of the flap |
length from hinged point of the flap to gravity centre of the flap | |
| m | mass of the flap |
| N | damping coefficient of PTO |
absorbed power of the device | |
available power irregular wave | |
time averaged power of incoming wave | |
frequency spectra of the sea | |
| T | time period of the incoming wave |
significant wave period | |
external coulomb damping moment on the flap | |
optimum coulomb damping moment at T = 12 s, and H = 1.35 m | |
impulse response function | |
| θ | angle of oscillation of the flap |
amplitude of angle of oscillation of the flap | |
| ω | frequency (rad/s) |
resonance frequency (rad/s) | |
| ρ | static density of water |
| λ | wave length |
non-dimensional wave length |
Appendix A. 2D potential theory for Pendulor device
Appendix A.1. Velocity Potential
Appendix A.1.1. Sea Side Velocity Potential
Appendix A.1.2. Chamber Side Velocity Potential
Appendix A.2. Hydrodynamic Parameters of the Device
Appendix A.2.1. Chamber Side Hydrodynamic Parameters
Appendix A.2.2. Sea Side Hydrodynamic Parameters
Appendix A.2.3. Excitation Moment
References
- Watabe, T.; Kondo, H.; Matsuda, T.; Yano, K.; Dote, Y.; Takagi, M. Method and Apparatus for Generating Electric Power by Waves. U.S. Patent 4,490,621, 25 December 1984. [Google Scholar]
- Watabe, T. “Pendulor” wave power converter—Fifteen years study and future prospect. In Proceedings of the International Symposium on Ocean Energy Development for Overcoming the Energy & Environmental Crises, Muroran, Hokkaido, Japan, 26–27 August 1993; pp. 41–52.
- Watabe, T.; Kondo, H.; Shirai, H.; Seino, K. Re-modeling of Muroran wave test plant. In Proceedings of the Forth International Offshore and Polar Engineering conference, Osaka, Japan, 10–15 April 1994; Volume 1, pp. 353–358.
- Watabe, T.; Yokouchi, H.; Kondo, H.; Inoya, M.; Kudo, M. Installation of the new “Pendulor” for the 2nd stage sea test. In Proceedings of the Ninth International Offshore and Polar Engineering Conference, Brest, France, 30 May–4 June 1999. Number ISOPE-I-99-021.
- Watabe, T.; Kondo, H. A new rotary vane pump for ocean wave power conversion. In Proceedings of the 2nd International Symposium on Fluid Power Transmission and Control ISFP’95, Shanghai, China, 5–7 October 1995; pp. 48–52.
- Kondo, H.; Watabe, T.; Yano, K. Wave power extraction at coastal structure by means of moving body in the chamber. Coast. Eng. 1984, 1, 2875–2891. [Google Scholar]
- Watabe, T. Utilization of the Ocean Wave Energy; Fuji Print Company Ltd.: Muroran, Japan, 2007. [Google Scholar]
- Park, J.; Shin, S.; Hong, K.; Kim, S. A study on the wave response and efficiency of a pendulum wave energy converter. In Proceedings of the Twenty-second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; pp. 601–606.
- Folley, M.; Whittaker, T.; Osterried, M. The oscillating wave surge converter. Int. J. Offshore Polar Eng. 2004, 1, 1–5. [Google Scholar]
- Gunawaradane, S.D.G.S.P.; Abeysekara, M.P.; Uyanwaththa, D.M.A.R.; Tennakoon, S.B.; Wijekoon, W.M.J.S.; Ranasinghe, R.A.P.C. Model study on “Pendulor” type wave energy device to utilize ocean wave energy in Sri Lanka. In Proceedings of the International Conference on Sustainable Built Environment (ICSBE-2010), Kandy, Sri Lanka, 13–14 December 2010; pp. 297–303.
- Watabe, T.; Yokouchi, H.; Gunawardane, S.; Obeyesekera, B.; Dissanayake, U. Preliminary study on wave energy utilization in Sri Lanka. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; Volume I, pp. 596–603.
- Ferri, F.; Ambühl, S.; Fischer, B.; Kofoed, J.P. Balancing power output and structural fatigue of wave energy converters by means of control strategies. Energies 2014, 7, 2246–2273. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Function and Ship Motions. 1962. Available online: https://dome.mit.edu/handle/1721.3/49049 (accessed on 6 April 2016).
- Taghipour, R.; Perez, T.; Moan, T. Hybrid frequency-time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar] [CrossRef]
- Duarte, T.; Sarmento, A.; Alves, M.; Jonkman, J. State-space realization of the wave-radiation force within FAST. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013.
- Chen, M.; Eatock, R.; Sang, Y. Time domain modeling of a dynamic impact oscillator under wave excitations. Ocean Eng. 2014, 76, 40–51. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J. Power capture performance of an oscillating-body WEC with nonlinear snap through PTO systems in irregular waves. Appl. Ocean Res. 2015, 52, 261–273. [Google Scholar] [CrossRef]
- Amarasekara, H.W.K.M.; Abeynayake, P.A.G.S.; Fernando, M.A.R.M.; Atputharajah, A.; Uyanwaththa, D.M.A.R.; Gunawardane, S.D.G.S.P.; Gerdin, L.; Keijser, M.; Fåhraeus, M.W.; Fernando, I.M.K.; et al. A prefeasibility study on ocean wave power generation for the Southern Coast of Sri Lanka: Electrical feasibility. Int. J. Distrib. Energy Resour. Smart Grids 2014, 10, 79–93. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interaction Including Wave Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Budal, K.; Falnes, J. Interacting Point Absorbers with Controlled Motion. In Power from Sea Waves; Count, B., Ed.; Academic Press: London, UK, 1980; pp. 381–399. [Google Scholar]
- Costa, P.R.; Garcia-Rosa, P.B.; Estefen, S.F. Phase control strategy for a wave energy hyperbaric converter. Ocean Eng. 2010, 37, 1483–1490. [Google Scholar] [CrossRef]
- Perez, T.; Fossen, T.I. Practical aspects of frequency-domain identification of dynamic models of marine structures from hydrodynamic data. Ocean Eng. 2011, 38, 426–435. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O. Modelling and control of oscillating-body wave energy converters with hydraulic power take-off and gas accumulator. Ocean Eng. 2007, 34, 2021–2032. [Google Scholar] [CrossRef]
- Deen, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Co. Pte. Ltd.: Singapore, Singapore, 2000; Volume 2. [Google Scholar]
- Anami, K.; Ishii, N.; Knisely, C.W. Added mass and wave radiation damping for flow-induced rotational vibrations of skinplates of hydraulic gates. J. Fluids Struct. 2012, 35, 213–228. [Google Scholar] [CrossRef]
- Lewandowski, E.M. The Dynamics of Marine Craft Maneuvering and Seakeeping; World Scientific Publishing Co. Pte. Ltd.: Singapore, Singapore, 2004; p. 420. [Google Scholar]
- Porter, R.; Biggs, N.R.T. Wave Energy Absorption by a Flap-Type Oscillating Wave Surge Converter. University of Bristol–Department of Mathematics–Study. Available online: http://www.maths.bris.ac.uk/marp/publications.html (accessed on 6 April 2016).
- Zurkinden, A.S.; Ferri, F.; Beatty, S.; Kofoed, J.P.; Kramer, M.M. Non-linear numerical modeling and experimental testing of a point absorber wave energy converter. Ocean Eng. 2014, 78, 11–21. [Google Scholar] [CrossRef]
- Ogilvie, T. Recent progress towards the understanding and prediction of ship motions. In Proceedings of the Fifth Symposium on Naval Hydrodynamics, Bergen, Norway, 10–12 September 1964.
- MATLAB User Manual; The MathWorks Inc: Natick, MA, USA, 2014.
- Murakami, T.; Imai, Y.; Nagata, S. Experimental study on load characteristics in a floating type pendulum wave energy converter. J. Therm. Sci. 2014, 23, 465–471. [Google Scholar] [CrossRef]
- Beards, C.F.; Eng, C. Structural Vibration: Analysis and Damping; Halsted Press, an imprint of John Wiley & Sons Inc: New York, NY, USA, 1996; p. 287. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing Co. Pte. Ltd.: Singapore, Singapore, 2000; Volume 15, p. 443. [Google Scholar]
- Scheffer, H.; Fernando, K.; Fittschen, T. Directional Wave Climate Study South-West Coast of Sri Lanka Report on the Wave Measurements off Galle; Sri Lankan–German Cooperation CCD-GTZ Coast Conservation Project: Colombo, Sri Lanka, 1994. [Google Scholar]
- Rusu, E. Evaluation of the wave energy conversion efficiency in various coastal environments. Energies 2014, 7, 4002–4018. [Google Scholar] [CrossRef]
- Wang, L.; Isberg, J. Nonlinear passive control of a wave energy converter subject to constraints in irregular waves. Energies 2015, 8, 6528–6542. [Google Scholar] [CrossRef]
- Watabe, T.; Yokouchi, H.; Gunawardane, S.D.G.S.P.; Thakker, A. Autonomous optimization control and the controllor for “Pendulor”. In Proceedings of the JFPS International Symposium on Fluid Power, Nara, Japan, 12–15 November 2002; pp. 843–848.
- Falcão, A.F.D.O. Phase control through load control of oscillating-body wave energy converters with hydraulic PTO system. Ocean Eng. 2008, 35, 358–366. [Google Scholar] [CrossRef]
- Folley, M.; Whittaker, T.J.T.; Henry, A. The effect of water depth on the performance of a small surging wave energy converter. Ocean Eng. 2007, 34, 1265–1274. [Google Scholar] [CrossRef]



















| Parameter | Unit |
|---|---|
| Still water height, h | 4 m |
| Chamber length, d | 18 m |
| Inner width of the chamber, b | 3 m |
| Flap length from hinge to still water level, l | 4 m |
| Flap mass, m | 3750 kg |
| Distance from the hinge to the flap centre of gravity, | 4.5 m |
| Design wave height, | 1 m |
| Design wave period | 12 s |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunawardane, S.P.; Kankanamge, C.J.; Watabe, T. Study on the Performance of the “Pendulor” Wave Energy Converter in an Array Configuration. Energies 2016, 9, 282. https://doi.org/10.3390/en9040282
Gunawardane SP, Kankanamge CJ, Watabe T. Study on the Performance of the “Pendulor” Wave Energy Converter in an Array Configuration. Energies. 2016; 9(4):282. https://doi.org/10.3390/en9040282
Chicago/Turabian StyleGunawardane, Sudath Prasanna, Chathura Jayan Kankanamge, and Tomiji Watabe. 2016. "Study on the Performance of the “Pendulor” Wave Energy Converter in an Array Configuration" Energies 9, no. 4: 282. https://doi.org/10.3390/en9040282
APA StyleGunawardane, S. P., Kankanamge, C. J., & Watabe, T. (2016). Study on the Performance of the “Pendulor” Wave Energy Converter in an Array Configuration. Energies, 9(4), 282. https://doi.org/10.3390/en9040282