Power Production Losses Study by Frequency Regulation in Weak-Grid-Connected Utility-Scale Photovoltaic Plants
Abstract
:1. Introduction
2. Frequency Regulation
2.1. Grid Code Requirements
2.2. Frequency Regulation Methods
2.3. Battery Energy Storage System Rule-Based Control
3. Frequency Regulation Behaviour Methods in Weak Grids
3.1. Weak Grids Frequency Excursions
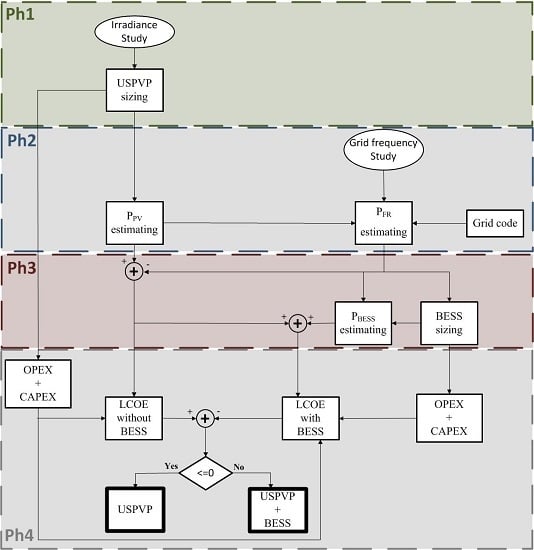
3.2. Utility-Scale PhotoVoltaic Plants Sizing
4. Frequency Regulation Results
4.1. Power Losses Applying Frequency Regulation
5. Battery Energy Storage System Results
5.1. Reducing Losses with Battery Energy Storage System
5.2. Battery Energy Storage System Life Cycle
5.3. Levelized Cost of Electricity Estimation
6. Conclusions
- Frequency excursions could remian for very long inside the range of FR, up to 50 min for some cases.
- However, the mean time of frequency excursions is much shorter, about 1 or 2 min for all studied cases.
- When the frequency fault exceeded the FR operating range, the fault duration could be significantly longer. This effect is due to the FR saturation control.
- Frequency excursions are hourly time dependent. The ocurrence probability of faults is higher in day time, increasing USPVP losses. Moreover, it is distributed irregularly with some remarked peaks, probably due to peak demand hours.
- BESS could improve other features as constant power ramp rates over production.
- Energy saved could be used at any time when the utility grid needs it, complementing the uncertainty of renewable sources. Moreover, BESS could perform perform peak shaving actions and load management.
- BESS could be used also as static voltage compensators (SVCs), adding reactive power capacity to the plant.
- BESS could smooth PV plant output production over cloudy conditions.
- BESS could be used to perform load shifting actions to help the grid stability.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Morjaria, M.; Anichkov, D.; Chadliev, V.; Soni, S. A grid-friendly plant: The role of utility-scale photovoltaic plants in grid stability and reliability. IEEE Power Energy Mag. 2014, 12, 87–95. [Google Scholar] [CrossRef]
- Grid Connection Code for Renewable Power Plants (RPPs) Connected to the Electricity Transmission System (TS) or the Distribution System (DS) in South Africa; Version 2.6; National Energy Regulator of South Africa (NERSA): Pretoria, South Africa, 2012.
- Guideline for Generating Plants, Connection to and Parallel Operation with the Medium-Voltage Network; German Association of Energy and Water Industries (BDEW): Berlin, Germany, 2008.
- Regolazione Tecnica dei Requisiti di Sistema Della Generazione Distribuita; Terna Group: Rome, Italy, 2012. (In Italian)
- Norma Técnica de Seguridad y Calidad de Servicio; Electric National Commission (CNE): Santiago de Chile, Chile, 2015. (In Spanish)
- Minimum Technical Requirements for Photovoltaic Generation (PV) Projects; Puerto Rico Electric Power Authority (PREPA): San Juan, Puerto Rico, 2012.
- Reglas Generales de Interconexión al Sistema Eléctrico; Comisión Federal de Electricidad (CFE): Mexico City, Mexico, 2014. (In Spanish)
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A voltage and frequency droop control method for parallel inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Lu, L.Y.; Chu, C.C. Autonomous Power Management and Load Sharing in Isolated Micro-Grids by Consensus-Based Droop Control of Power Converters. In Proceedings of the Future Energy Electronics Conference, Tainan, Taiwan, 3–6 November 2013; pp. 365–370.
- Xin, H.; Liu, Y.; Wang, Z.; Gan, D.; Yang, T. A new frequency regulation strategy for photovoltaic systems without energy storage. IEEE Trans. Sustain. Energy 2013, 4, 985–993. [Google Scholar] [CrossRef]
- Vasconcelos, H.; Moreira, C.; Madureira, A.; Lopes, J.P.; Miranda, V. Advanced control solutions for operating isolated power systems: Examining the Portuguese islands. IEEE Electrific. Mag. 2015, 3, 25–35. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, H.; Wang, Z.; Gan, D. Control of virtual power plant in microgrids: a coordinated approach based on photovoltaic systems and controllable loads. IET Gener. Transm. Distrib. 2015, 9, 921–928. [Google Scholar] [CrossRef]
- Trivedi, A.; Jain, D.; Singh, M. A Modified Droop Control Method for Parallel Operation of VSI’s in Microgrid. In Proceedings of the IEEE ISGT Asia, Bangalore, India, 10–13 November 2013; pp. 1–5.
- Kahrobaeian, A.; Mohamed, Y.R. Robust single-loop direct current control of LCL-filtered converter-based DG units in grid-connected and autonomous microgrid modes. IEEE Trans. Power Electron. 2014, 29, 5605–5619. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; RodriÌAguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Ashabani, M.; Mohamed, Y.A.R.I. Integrating VSCs to weak grids by nonlinear power damping controller with self-synchronization capability. IEEE Trans. Power Syst. 2014, 29, 805–814. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. A power management strategy for PV/battery hybrid systems in islanded microgrids. IEEE Trans. Power Syst. 2014, 2, 870–882. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dorfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary frequency and voltage control of islanded microgrids via distributed averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Yuen, C.; Oudalov, A.; Timbus, A. The provision of frequency control reserves from multiple microgrids. IEEE Trans. Ind. Electron. 2011, 58, 173–183. [Google Scholar] [CrossRef]
- Shi, H.T.; Zhuo, F.; Yi, H.; Wang, F.; Zhang, D.; Geng, Z. A novel real-time voltage and frequency compensation strategy for photovoltaic-based microgrid. IEEE Trans. Ind. Electron. 2015, 62, 3545–3556. [Google Scholar] [CrossRef]
- Chow, J.H.; Wu, F.F.; Momoh, J.A. Applied Mathematics for Restructured Electric Power Systems; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Balancing and Frequency Control; North American Electric Reliability Corporation: Princeton, NJ, USA, 2011.
- Hanley, M.A. Frequency Instability Problems in North American Interconnections; National Energy Technology Laboratory: Pittsburgh, PA, USA, 2011. [Google Scholar]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-connected photovoltaic systems: An overview of recent research and emerging PV converter technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Romero-Cadaval, E.; Spagnuolo, G.; Franquelo, L.G.; Ramos-Paja, C.A.; Suntio, T.; Xiao, W.M. Grid-connected photovoltaic generation plants: Components and operation. IEEE Ind. Electron. Mag. 2013, 7, 6–20. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Hui, D.; Lai, X. Battery energy storage station (BESS)-based smoothing control of photovoltaic (PV) and wind power generation fluctuations. IEEE Trans. Sustain. Energy 2013, 4, 464–473. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Aichhorn, A.; Zheng, J.; Greenleaf, M. Sizing strategy of distributed battery storage system with high penetration of photovoltaic for voltage regulation and peak load shaving. IEEE Trans. Smart Grid 2014, 5, 982–991. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.R.I. Market-oriented energy management of a hybrid wind-battery energy storage system via model predictive control with constraints optimizer. IEEE Trans. Ind. Electron. 2015, 62, 6658–6670. [Google Scholar] [CrossRef]
- Graditi, G.; Ippolito, M.G.; Telaretti, E.; Zizzo, G. An innovative conversion device to the grid interface of combined RES-based generators and electric storage systems. IEEE Trans. Ind. Electron. 2015, 62, 2540–2550. [Google Scholar] [CrossRef]
- DiOrio, N.; Dobos, A.; Janzou, S. Economic Analysis Case Studies of Battery Energy Storage with SAM; National Renewable Energy Laboratory: Denver, CO, USA, 2015. [Google Scholar]
- Battery Storage for Renewables: Market Status and Technology Outlook; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2015.
- Ekus, B. Storage Incentives or Demand Side Management: Is PV on the Right Track? International Battery & Energy Storage Alliance: Paris, France, 2015. [Google Scholar]
- Integrated Resource Planning Report; Hawaiian Electric Company: Honolulu, HI, USA, 2013.
- Gomez-Exposito, A.; Conejo, A.J.; Cañizares, C. Electric Energy Systems: Analysis and Operation; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Roberts, O.; Andreas, A. United States Virgin Islands: St. Thomas (Bovoni) & St. Croix (Longford) (Data); National Renewable Energy Laboratory, CS Division, University of California: Oakland, CA, USA, 1997. [Google Scholar]
- Solutions for Utility-Scale, Power Management and Grid Integration; GPTech: Seville, Spain, 2015.
- Sunny Central 800 MV/1000 MV/1250 MV Datasheet; SMA Solar Technology AG: Rocklin, CA, USA, 2015.
- Ingecon Sun 830TL B300 Indoor Datasheet; Ingetam: Sarrigurem, Spain, 2015.
- Lave, M.; Ellis, A.; Stein, J.S. Simulating Solar Power Plant Variability: A Review of Current Methods; Sandia National Laboratories: Alburquerque, NM, USA, 2013. [Google Scholar]
- Lave, M.; Kleissl, J.; Stein, J.S. A wavelet-based variability model (WVM) for solar PV power plants. IEEE Trans. Sustain. Energy 2013, 4, 501–509. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J. Testing a Wavelet-Based Variability Model (WVM) for Solar PV Power Plants. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–6.
- Lithium Battery Life; La Société des Accumulateurs Fixes et de Traction (SAFT): Bagnolet, France, 2014.
- Intensium Max 20P High Power Lithium-Ion Container; La Société des Accumulateurs Fixes et de Traction (SAFT): Bagnolet, France, 2013.
- Advanced Battery for Energy Storage System; Lucky Goldstar Chemicals (LG Chem): Seoul, Korea, 2015.
- Levelized Cost of Electricity: Renewable Energy Technologies Study; Franhofer ISE: Freiburg, Germany, 2013.
- Lazard’s Levelized Cost of Electricity Analysis Version 8.0; Lazard: New York, NY, USA, 2014.
- Sarasa-Maestro, C.; Dulfo-López, R.; Bernal-Agustín, J. Photovoltaic remuneration policies in the European Union. Energy Policy 2013, 55, 317–328. [Google Scholar] [CrossRef]
- Badcock, J.; Lenzen, M. Subsidies for electricity-generating technologies: A review. Energy Policy 2010, 38, 5038–5047. [Google Scholar] [CrossRef]
- López Polo, A.; Haas, R. An international overview of promotion policies for grid-connected photovoltaic systems. Prog. Photovolt. Res. Appl. 2014, 22, 248–273. [Google Scholar] [CrossRef]
- Sgroi, F.; Tudisca, S.; Di Trapani, A.; Testa, R.; Squatrito, R. Efficacy and efficiency of Italian energy policy: The case of PV systems in greenhouse farms. Energies 2014, 7, 3985–4001. [Google Scholar] [CrossRef]
- Giannini, E.; Moropoulou, A.; Maroulis, Z.; Siouti, G. Penetration of Photovoltaics in Greece. Energies 2015, 8, 6497–6508. [Google Scholar] [CrossRef]






















| Country | FRT | FR |
|---|---|---|
| Germany (BDEW) |  |  |
| Italy (CEI) |  |  |
| South Africa (NERSA) |  |  |
| Mexico (CFE) |  |  |
| Puerto Rico (PREPA) |  |  |
| Chile (CNE) |  |  |
| Parameter | Chile | Puerto Rico |
|---|---|---|
| Power plant capacity | 300 MW | 300 MW |
| PV panels density | 41 W/m | 41 W/m |
| PV plant area | square | square |
| PV panels tilt | ||
| Cloud speed | 10 m/s | 10 m/s |
| Latitude | ||
| Longitude |
| Parameter | Chile | Puerto Rico |
|---|---|---|
| Start droop over frequency () | 50.2 Hz | 60.012 Hz |
| Stop droop over frequency () | 50.5–52 Hz | 60.3 Hz |
| Maximum droop over frequency () | 1 p.u. | 1 p.u. |
| Start droop under frequency () | N/A | 59.988 Hz |
| Stop droop under frequency () | N/A | 59.7 Hz |
| Maximum droop under frequency () | N/A | 0.1 p.u. |
| Recovery ramp rate () | 0.2 p.u./s. | N/A |
| BESS Settings | |||||
|---|---|---|---|---|---|
| Parameter | |||||
| Value | 0.1 p.u. | 0.1 p.u. | 0.02 p.u. | 0.2 p.u. | 0.9 p.u. |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Debt | Debt interest | ||
| Tax equity | Tax equity interest | ||
| Equity | Equity interest | ||
| - | - | WACC |
| Description | Case | Chile | Puerto Rico |
|---|---|---|---|
| BESS | Technology | Li-ion | Li-ion |
| Nominal power | 30 MW | 30 MW | |
| Capacity | 0.15 hp.u. | 0.25 hp.u. | |
| Capital cost | 1.5 /Wh | 1.5 /Wh | |
| Efficency cycle | |||
| Facility life | 20 years | 20 years | |
| O&M costs | 165,000 /year | 165,000 /year | |
| USPVP | Technology | Polycristaline | Polycristaline |
| Nominal power | 300 MW | 300 MW | |
| Capital cost | 0.86 /Wh | 0.86 /Wh | |
| Facility life | 20 years | 20 years | |
| O&M costs | 6,000,000 /year | 6,000,000 /year |
| Country | Case | Without BESS | With BESS |
|---|---|---|---|
| Chile | Production | 749 GWh/year | 767 GWh/year |
| OPEX | $ | $ | |
| CAPEX | $ | $ | |
| LCOE | 46.83 /MWh | 46.82 /MWh | |
| Puerto Rico | Production | 656 GWh/year | 702 GWh/year |
| OPEX | $ | $ | |
| CAPEX | $ | $ | |
| LCOE | 53.50 /MWh | 51.99 /MWh |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz-Cruzado-Alba, J.; Rojas, C.A.; Kouro, S.; Galván Díez, E. Power Production Losses Study by Frequency Regulation in Weak-Grid-Connected Utility-Scale Photovoltaic Plants. Energies 2016, 9, 317. https://doi.org/10.3390/en9050317
Muñoz-Cruzado-Alba J, Rojas CA, Kouro S, Galván Díez E. Power Production Losses Study by Frequency Regulation in Weak-Grid-Connected Utility-Scale Photovoltaic Plants. Energies. 2016; 9(5):317. https://doi.org/10.3390/en9050317
Chicago/Turabian StyleMuñoz-Cruzado-Alba, Jesús, Christian A. Rojas, Samir Kouro, and Eduardo Galván Díez. 2016. "Power Production Losses Study by Frequency Regulation in Weak-Grid-Connected Utility-Scale Photovoltaic Plants" Energies 9, no. 5: 317. https://doi.org/10.3390/en9050317
APA StyleMuñoz-Cruzado-Alba, J., Rojas, C. A., Kouro, S., & Galván Díez, E. (2016). Power Production Losses Study by Frequency Regulation in Weak-Grid-Connected Utility-Scale Photovoltaic Plants. Energies, 9(5), 317. https://doi.org/10.3390/en9050317