A Review of Wave-to-Wire Models for Wave Energy Converters
Abstract
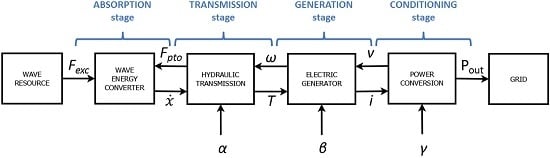
:1. Introduction
- Absorption stage
- Transmission stage
- Generation stage
- Conditioning stage
1.1. Existing Wave-to-Wire Models
- Balanced parsimonious models for each stage of the drive train (including nonlinearities where required);
- Consideration of all possible control inputs at the various stages in the drive train;
- Articulation of constraints, energy losses and efficiency curves for each component;
- Specification of physical constraints for each component, e.g., displacement, velocity and force (for mechanical components), pressure (for hydraulic components), current, voltage (for electrical components) and power specification (at all levels). The specification of electrical grid constraints, including power quality measures, is also important, as appropriate.
1.2. The Control Problem
2. Absorption Stage
3. Transmission Stage
3.1. Pneumatic Transmission
3.1.1. Hydrodynamics for OWC Converters
3.1.2. Thermodynamics in the Chamber
3.1.3. Air Turbines
3.2. Hydraulic Transmission
3.2.1. Hydraulic Cylinder
Discrete Displacement Cylinder
3.2.2. Valves
3.2.3. Hydraulic Motor
- Bent-axis
- Swash-plate
- Digital Displacement
3.2.4. Accumulators
3.2.5. Hoses
3.3. Mechanical Transmission
3.3.1. Rack and Pinion Mechanism
3.3.2. Belt Drive System
3.3.3. Ratchet Wheel Mechanism
3.3.4. Screw Mechanisms
3.4. Magnetic Transmission
4. Generation Stage
4.1. Rotary Generation
4.1.1. Fixed-Speed Generation
4.1.2. Variable-Speed Generation
4.2. Direct Conversion
4.2.1. Linear Permanent Magnet Generators
4.2.2. Snapper
5. Conditioning Stage
6. The Electricity Network
6.1. Voltage Variations
6.2. Frequency Variations
6.3. Voltage Waveform Quality
6.3.1. Harmonic Correction
6.3.2. Phase Imbalance
6.3.3. Rapid Fluctuations-Flicker
6.4. Renewable Energy Sources
6.4.1. Ride through Capability after Voltage Sags
6.4.2. Reactive Power
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sjolte, J. Marine Renewable Energy Conversion: Grid and Off-Grid Modeling, Design and Operation. Ph.D. Thesis, Norges Teknisk-Naturvitenskapelige Universitet (NTNU), Fakultet for Informasjonsteknologi, Matematikk og Elektroteknikk, Institutt for Elkraftteknikk, Trondheim, Norway, 2014. [Google Scholar]
- Babarit, A.; Hals, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]
- De Andrés, A.D.; Guanche, R.; Armesto, J.A.; del Jesus, F.; Vidal, C.; Losada, I.J. Time domain model for a two-body heave converter: Model and applications. Ocean Eng. 2013, 72, 116–123. [Google Scholar] [CrossRef]
- De Andrés, A.D.; Guanche, R.; Weber, J.W.; Costello, R. Finding gaps on power production assessment on WECs: Wave definition analysis. Renew. Energy 2015, 83, 171–187. [Google Scholar] [CrossRef]
- Robertson, B.; Bailey, H.; Clancy, D.; Ortiz, J.P.; Buckham, B.J. Influence of wave resource assessment methodology on wave energy production estimates. Renew. Energy 2016, 86, 1145–1160. [Google Scholar] [CrossRef]
- Igic, P.; Zhou, Z.; Knapp, W.; MacEnri, J.; Sorensen, H.C.; Friis-Madsen, E. Multi-megawatt offshore wave energy converters—Electrical system configuration and generator control strategy. IET Renew. Power Gener. 2011, 5, 10–17. [Google Scholar] [CrossRef]
- Amundarain, M.; Alberdi, M.; Garrido, A.J.; Garrido, I. Modeling and Simulation of Wave Energy Generation Plants: Output Power Control. IEEE Trans. Ind. Electron. 2011, 58, 105–117. [Google Scholar] [CrossRef]
- Josset, C.; Babarit, A.; Clément, A.H. A wave-to-wire model of the SEAREV wave energy converter. Proc. Inst. Mech. Eng. Part M: J. Eng. Marit. Environ. 2007, 221, 81–93. [Google Scholar] [CrossRef]
- Ricci, P.; Lopez, J.; Santos, M.; Ruiz-Minguela, P.; Villate, J.L.; Salcedo, F.; Falcão, A.F.O. Control strategies for a wave energy converter connected to a hydraulic power take-off. IET Renew. Power Gener. 2011, 5, 234–244. [Google Scholar] [CrossRef]
- Garcia-Rosa, P.B.; Vilela Soares Cunha, J.P.; Lizarralde, F.; Estefen, S.F.; Machado, I.R.; Watanabe, E.H. Wave-to-Wire Model and Energy Storage Analysis of an Ocean Wave Energy Hyperbaric Converter. IEEE J. Ocean. Eng. 2014, 39, 386–397. [Google Scholar] [CrossRef]
- Bailey, H.; Ortiz, J.P.; Robertson, B.; Buckhamn, B.J.; Nicoll, R.S. A methodology for wave-to-wire wec simulations. In Proceedings of the 2nd Marine Energy Technology Symposium (METS), Seattle, WA, USA, 15–18 April 2015.
- Forehand, D.I.; Kiprakis, A.E.; Nambiar, A.J.; Wallace, A.R. A Fully Coupled Wave-to-Wire Model of an Array of Wave Energy Converters. IEEE Trans. Sustain. Energy 2015, 7, 118–128. [Google Scholar] [CrossRef]
- Hansen, R.H. Design and Control of the PowerTake-Off System for a Wave Energy Converter with Multiple Absorbers. Ph.D. Thesis, Aalborg Universitet, Aalborg, Denmark, 2013. [Google Scholar]
- Tedeschi, E.; Carraro, M.; Molinas, M.; Mattavelli, P. Effect of Control Strategies and Power Take-Off Efficiency on the Power Capture From Sea Waves. IEEE Trans. Energy Convers. 2011, 26, 1088–1098. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.P.; Ju, P.; Sterling, M.J. Modeling and Control of AWS-Based Wave Energy Conversion System Integrated Into Power Grid. IEEE Trans. Power Syst. 2008, 23, 1196–1204. [Google Scholar]
- O Sullivan, A.C.; Lightbody, G. Wave to Wire Power Maximisation from a Wave Energy Converter. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- Ringwood, J.V.; Bacelli, G.; Fusco, F. Energy-Maximizing Control of Wave-Energy Converters: The Development of Control System Technology to Optimize Their Operation. IEEE Control Syst. 2014, 34, 30–55. [Google Scholar] [CrossRef]
- Paparella, F.; Monk, K.; Winands, V.; Lopes, M.F.; Conley, D.; Ringwood, J.V. Up-wave and autoregressive methods for short-term wave forecasting for an oscillating water column. IEEE Trans. Sustain. Energy 2015, 6, 171–178. [Google Scholar] [CrossRef]
- Fusco, F.; Ringwood, J.V. Short-term wave forecasting for real-time control of wave energy converters. IEEE Trans. Sustain. Energy 2010, 1, 99–106. [Google Scholar] [CrossRef]
- Penalba, M.; Mérigaud, A.; Gilloteaux, J.C.; Ringwood, J.V. Nonlinear Froude-Krylov force modelling for two heaving wave energy point absorbers. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- Bacelli, G.; Genest, R.; Ringwood, J.V. Nonlinear control of flap-type wave energy converter with a non-ideal power take-off system. Annu. Rev. Control 2015, 40, 116–126. [Google Scholar] [CrossRef]
- Genest, R.; Bonnefoy, F.; Clément, A.H.; Babarit, A. Effect of non-ideal power take-off on the energy absorption of a reactively controlled one degree of freedom wave energy converter. Appl. Ocean Res. 2014, 48, 236–243. [Google Scholar] [CrossRef]
- Hals, J.; Falnes, J.; Moan, T. Constrained optimal control of a heaving buoy wave-energy converter. J. Offshore Mech. Arct. Eng. 2011, 133, 011401. [Google Scholar] [CrossRef] [Green Version]
- Bacelli, G.; Ringwood, J.V. Numerical optimal control of wave energy converters. IEEE Trans. Sustain. Energy 2015, 6, 294–302. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Function and Ship Motions; AD0288277; DTIC: Washington, DC, USA, 1962; pp. 101–109. [Google Scholar]
- Bacelli, G.; Ringwood, J.V. Numerical optimal control of wave energy converters. IEEE Trans. Sustain. Energy 2015, 6, 294–302. [Google Scholar] [CrossRef]
- Paparella, F.; Bacelli, G.; Paulmeno, A.; Mouring, S.E.; Ringwood, J.V. Multibody Modelling of Wave Energy Converters Using Pseudo-Spectral Methods With Application to a Three-Body Hinge-Barge Device. IEEE Trans. Susta. Energy 2016, 7, 966–974. [Google Scholar] [CrossRef]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- WAMIT Inc., M. WAMIT v7.0 Manual; WAMIT Inc., M.: Chestnut Hill, MA, USA, 2013. [Google Scholar]
- Zurkinden, A.S.; Ferri, F.; Beatty, S.; Kofoed, J.P.; Kramer, M.M. Non-linear numerical modeling and experimental testing of a point absorber wave energy converter. Ocean Eng. 2014, 78, 11–21. [Google Scholar] [CrossRef]
- Giorgi, S.; Davidson, J.; Ringwood, J.V. Identification of nonlinear excitation force kernels using numerical wave tank experiments. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- Merigaud, A.; Gilloteaux, J.C.; Ringwood, J.V. A nonlinear extension for linear boundary element methods in wave energy device modelling. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 615–621.
- Gilloteaux, J.C. Mouvements de Grande Amplitude d’un Corps Flottant en Fluide Parfait. Application a la Recuperation de L’energie des Vagues. Ph.D. Thesis, Ecole Centrale de Nantes (ECN), Nantes, France, 2007. [Google Scholar]
- Bhinder, M.A.; Babarit, A.; Gentaz, L.; Ferrant, P. Assessment of Viscous Damping via 3D-CFD Modelling of a Floating Wave Energy Device. In Proceedings of the 9th European Wave and Tidal Energy Conference (EWTEC), Southampton, UK, 5–9 September 2011.
- Kramer, M.; Ferri, F.; Zurkinden, A.; Vidal, E.; Kofoed, J.P. Experimental Validation of Numerical Models for Wave Energy Absorbers. In Proceedings of the 2nd SDWED symposium, Advances in Modelling of Wave Energy Devices, Lyngby, Denmark, 26 April 2012.
- Ferri, F.; Kramer, M.M.; Pecher, A. Validation of a wave-body interaction model by experimental tests. In Proceedings of the The Twenty-third International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, Anchorage, Alaska, 30 June–4 July 2013.
- Previsic, M.; Shoele, K.; Epler, J. Validation of Theoretical Performance Results using Wave Tank Testing of Heaving Point Absorber Wave Energy Conversion Device working against a Subsea Reaction Plate; Technical report; ReVision Consulting: Sacramento, CA, USA, 2014. [Google Scholar]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Review of Non-Linear Approaches for Wave Energy Converter Modelling. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 1–6 September 2015.
- Bhinder, M.A.; Babarit, A.; Gentaz, L.; Ferrant, P. Effect of viscous forces on the performance of a surging wave energy converter. In Proceedings of the The Twenty-second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012.
- Morison, J.R.; O’Brien, M.P.; Johnson, J.W.; Schaaf, S.A. The forces exerted by surface waves on pliles. Petroleum Trans. AIME. 1950, 189, 149–157. [Google Scholar]
- Heath, T.; Whittaker, T.J.T.; Boake, C.B. The design, construction and operation of the LIMPET wave energy converter (Islay, Scotland). In Proceedings of the 4th European Wave Energy Conference, Aalborg, Denmark, 4–6 December 2000.
- Taylor, J.; Caldwell, N. Design and construction of the variable-pitch air turbine for the Azores wave energy plant. In Proceedings of the Third European Wave Power Conference, Patras, Greece; 1998; Volume 30. [Google Scholar]
- Torre-Enciso, Y.; Ortubia, I.; López de Aguileta, L.I.; Marqués, J. Mutriku Wave Power Plant: From the thinking out to the reality. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009; pp. 319–329.
- Falcão, A.F.O.; Henriques, J.C.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Rea, J.; Kelly, J.; Alcorn, R.; O’Sullivan, D. Development and operation of a power take off rig for ocean energy research and testing. In Proceedings of the European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011.
- Alcorn, R.; Blavette, A.; Healy, M.; Lewis, A. FP7 EU funded CORES wave energy project: A coordinators’ perspective on the Galway Bay sea trials. Underw. Technol. 2014, 32, 51–59. [Google Scholar] [CrossRef]
- Washio, Y.; Osawa, H.; Nagata, Y.; Fujii, F.; Furuyama, H.; Fujita, T. The offshore floating type wave power device “Mighty Whale”: Open sea tests. In Proceedings of the Tenth International Offshore and Polar Engineering Conference, Seattle, WA, USA, 27 May–2 June 2000.
- Weber, J.W.; Thomas, G.P. An investigation into the importance of the air chamber design of an oscillating water column wave energy device. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001.
- Sheng, W.; Alcorn, R.; Lewis, A. Assessment of primary energy conversions of oscillating water columns. I. Hydrodynamic analysis. J. Renew. Sustain. Energy 2014, 6, 053113. [Google Scholar] [CrossRef]
- Sheng, W.; Alcorn, R.; Lewis, A. Assessment of primary energy conversions of oscillating water columns. II. Power take-off and validations. J. Renew. Sustain. Energy 2014, 6, 053114. [Google Scholar] [CrossRef]
- Kelly, J.F.; Wright, W.M.D.; Sheng, W.; O’Sullivan, K. Implementation and Verification of a Wave-to-Wire Model of an Oscillating Water Column With Impulse Turbine. IEEE Trans. Sustain. Energy 2016, 7, 546–553. [Google Scholar] [CrossRef]
- Evans, D.V. The oscillating water column wave-energy device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Sarmento, A.J.N.A. Wave generation by a periodic surface pressure and its application in wave-energy extraction. In Proceedings of the 15th International Congress of Theoritical and Applied Mechanics, Toronto, ON, Canada, 17–23 August 1980.
- Evans, D.V. Wave-power absorption by systems of oscillating surface pressure distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Evans, D.V. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Falcão, A.F.O. Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion. Renew. Energy 2012, 44, 328–339. [Google Scholar] [CrossRef]
- Sarmento, A.J.N.A.; Falcão, A.F.O. Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 1985, 150, 467–485. [Google Scholar] [CrossRef]
- Jefferys, R.; Whittaker, T. Latching control of an oscillating water column device with air compressibility. In Hydrodynamics of Ocean Wave-Energy Utilization; Springer: Berlin, Germany, 1986; pp. 281–291. [Google Scholar]
- Sheng, W.; Alcorn, R.; Lewis, A. On thermodynamics in the primary power conversion of oscillating water column wave energy converters. J. Renew. Sustain. Energy 2013, 5, 023105. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Justino, P.A.P. OWC wave energy devices with air flow control. Ocean Eng. 1999, 26, 1275–1295. [Google Scholar] [CrossRef]
- Henriques, J.C.C.; Gato, L.M.C.; Lemos, J.M.; Gomes, R.P.F.; Falcão, A.F.O. Peak-power control of a grid-integrated oscillating water column wave energy converter. Energy 2016, 109, 378–390. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Rodrigues, R.J.A. Stochastic modelling of OWC wave power plant performance. Appl. Ocean Res. 2002, 24, 59–71. [Google Scholar] [CrossRef]
- Thakker, A.; Jarvis, J.; Sahed, A. Design charts for impulse turbine wave energy extraction using experimental data. Renew. Energy 2009, 34, 2264–2270. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Falcão, A.F.O.; Gato, L.M.C. Air Turbines. In Comprehensive Renewable Energy; Sayigh, A., Ed.; Elsevier: Oxford, UK, 2012; pp. 111–149. [Google Scholar]
- Wells, A.A. Fluid driven rotary transducer. Br. Pat. Spec. 1976, 1, 595–700. [Google Scholar]
- Setoguchi, T.; Santhakumar, S.; Maeda, H.; Takao, M.; Kaneko, K. A review of impulse turbines for wave energy conversion. Renew. Energy 2001, 23, 261–292. [Google Scholar] [CrossRef]
- Cruz, J. Ocean Wave Energy: Current Status and Future Prespectives; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Curran, R.; Denniss, T.; Boake, C.B. Multidisciplinary design for performance: ocean wave energy conversion. In Proceedings of the Tenth International Offshore and Polar Engineering Conference, Seattle, WA, USA, 27 May–2 June 2 2000.
- Finnigan, T.; Auld, D. Model testing of a variable-pitch aerodynamic turbine. In Proceedings of the Thirteenth International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003.
- Falcão, A.F.O.; Gato, L.M.C.; Nunes, E.P.A.S. A novel radial self-rectifying air turbine for use in wave energy converters. Renew. Energy 2013, 50, 289–298. [Google Scholar] [CrossRef]
- Raghunathan, S. The Wells air turbine for wave energy conversion. Prog. Aerosp. Sci. 1995, 31, 335–386. [Google Scholar] [CrossRef]
- Faÿ, F.X.; Henriques, J.C.C.; Robles, E.; Marcos, M. Review of control strategies for oscillating water column wave energy converters. In Proceedings of the European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- Hoskin, R.E.; Count, B.M.; Nichols, N.K.; Nicol, D.A.C. Phase Control for the Oscillating Water Column; Hydrodynamics of Ocean Wave-Energy Utilization: IUTAM Symposium Lisbon/Portugal 1985; Springer: Berlin/Heidelberg, Germany, 1985; pp. 257–268. [Google Scholar]
- Henriques, J.C.C.; Gato, L.M.C.; Falcão, A.F.O.; Robles, E.; Faÿ, F.X. Latching control of a floating oscillating-water-column wave energy converter. Renew. Energy 2016, 90, 229–241. [Google Scholar] [CrossRef]
- Gato, L.M.C.; Falcão, A.F.O. Aerodynamics of the wells turbine: Control by swinging rotor-blades. Int. J. Mech. Sci. 1989, 31, 425–434. [Google Scholar] [CrossRef]
- Gato, L.M.C.; Eça, L.R.C.; Falcão, A.F.O. Performance of the Wells turbine with variable pitch rotor blades. J. Energy Resour. Technol. 1991, 113, 141–146. [Google Scholar] [CrossRef]
- Henriques, J.C.C.; Gomes, R.P.F.; Gato, L.M.C.; Falcão, A.F.O.; Robles, E.; Ceballos, S. Testing and control of a power take-off system for an oscillating-water-column wave energy converter. Renew. Energy 2016, 85, 714–724. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Vieira, L.C.; Justino, P.A.P.; André, J.M.C.S. By-pass air-valve control of an OWC wave power plant. J. Offshore Mech. Arctic Eng. 2003, 125, 205–210. [Google Scholar] [CrossRef]
- Falcão, A.F.O. Control of an oscillating-water-column wave power plant for maximum energy production. Appl. Ocean Res. 2002, 24, 73–82. [Google Scholar] [CrossRef]
- Jelali, M.; Kroll, A. Hydraulic Servo-Systems: Modelling, Identification and Control; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Yeaple, F. Fluid Power Design Handbook; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Olsson, H.; Åström, K.J.; De Wit, C.C.; Gäfvert, M.; Lischinsky, P. Friction models and friction compensation. Eur. J. Control 1998, 4, 176–195. [Google Scholar] [CrossRef]
- Hansen, R.H.; Andersen, T.O.; Pedersen, H.C. Model based design of efficient power take-off systems for wave energy converters. In Proceedings of the 12th Scandinavian International Conference on Fluid Power, Tampere, Finland, 18–20 May 2011.
- Hals, J.; Taghipour, R.; Moan, T. Dynamics of a force-compensated two-body wave energy converter in heave with hydraulic power take-off subject to phase control. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007.
- Kalinin, V. A Wave Energy Conversion System. WO Patent WO2009153329 A3, January 2011. [Google Scholar]
- Pizer, D.; Retzler, C.; Yemm, R. Floating Apparatus and Method for Extracting Power from Sea Waves. WO Patent WO2000017519 A1, March 2000. [Google Scholar]
- Hansen, R.H.; Kramer, M.M.; Vidal, E. Discrete displacement hydraulic power take-off system for the wavestar wave energy converter. Energies 2013, 6, 4001–4044. [Google Scholar] [CrossRef]
- Hansen, R.H.; Andersen, T.O.; Pedersen, H.C.; Hansen, A.H. Control of a 420 KN Discrete Displacement Cylinder Drive for the Wavestar Wave Energy Converter. In Proceedings of the ASME/BATH 2014 Symposium on Fluid Power and Motion Control, Bath, UK, 10–12 September 2014; pp. V001T01A021–V001T01A021.
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Renew. Energy 2006, 31, 271–283. [Google Scholar] [CrossRef]
- Salter, S.H.; Rampen, W.H.S. The Wedding Cake Multi-Eccentric Radial Piston Hydraulic Machine with Direct Computer Control of Displacement. In Proceedings of the 10th International Conference on Fluid Power, Brugge, Belgium, 5–7 April 1993; pp. 47–64.
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors : Principles, Design, Performance, Modelling, Analysis, Control and Testing; Tech Books International: New Delhi, India, 2003. [Google Scholar]
- Costello, R.; Ringwood, J.V.; Weber, J.W. Comparison of two alternative hydraulic PTO concepts for wave energy conversion. In Proceedings of the 9th European Wave and Tidal Energy Conference (EWTEC), Southampton, UK, 5–9 September 2011.
- Hansen, R.H.; Andersen, T.O.; Perdersen, H.C. Analysis of discrete pressure level systems for wave energy converters. In Proceedings of the International Conference on Fluid Power and Mechatronics (FPM), Beijing, China, 17–20 August 2011; pp. 552–558.
- Andersen, T.O.; Hansen, R.H.; Hansen, A. Simulation of Utilisation of Pressure Propagation for Increased Efficiency of Secondary Controlled Discrete Displacement Cylinders. In Proceedings of the 16th International Conference on Fluid Dynamic and Mechanical & Electrical Control Engineering (FDMECE), Chongqing, China, 10–11 November 2012.
- Stella, J.P.L.; Tornabene, M.G. Ocean Wave Energy Device. US Patent US4,599,858, 15 July 1986. [Google Scholar]
- Corey, G. Rack and Pinion Wave Motor Power Plant. US Patent US4,108,578, 22 August 1978. [Google Scholar]
- Eder, J.; Stewart, D. Wave Energy Converter and Power Take Off System. US Patent US8487459 B2, 14 April 2011. [Google Scholar]
- CorPower Ocean AB. Available online: http://www.corpowerocean.com/ (accessed on 27 June 2016).
- Albady, D.; Öhman, C. Characterization of a Cascade Gear Box for a Wave Energy Converter. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2013. [Google Scholar]
- Hals, J.; Ásgeirsson, S.G.; Hjálmarsson, E.; Maillet, J.; Moller, P.; Pires, P.; Guérinel, M.; Lopes, M. Tank testing of an inherently phase controlledWave Energy Converter. In Proceedings of the 11th EuropeanWave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- Metcalfe, M. Gearing up for efficiency. Gear Solut. 2012, 10, 50–55. [Google Scholar]
- Hansen, N.A.; Hansen, K.K. Wave Power Machine. US Patent US6,925,800, 9 August 2005. [Google Scholar]
- Pecher, A.; Kofoed, J.P.; Larsen, T. Design specifications for the Hanstholm WEPTOS wave energy converter. Energies 2012, 5, 1001–1017. [Google Scholar] [CrossRef]
- Merk, K. Device for Generating Energy Using Water Waves. WO Patent App. PCT/DE1998/001,087, 14 October 1999. [Google Scholar]
- Barness Industries Ltd. Precision Ball Screws. Available online: http://www.barnesballscrew.com/ball-screws/ (accessed on 27 June 2016).
- SKF Group leaflet. Roller Screws; PUB MT/P1 14489 EN; SKF Group: Gothenburg, Sweden, April 2014. [Google Scholar]
- Stewart, D.; Gerber, J. Wave Energy Converter Utilizing Internal Reaction Mass and Spring. CA Patent 2,632,158, 17 February 2015. [Google Scholar]
- Buoy and Ball Screw Combined Sea Wave Generator. CN Patent App. CN 200,910,180,062, 4 May 2011.
- Agamloh, E.B.; Wallace, A.K.; von Jouanne, A. A novel direct-drive ocean wave energy extraction concept with contact-less force transmission system. Renew. Energy 2008, 33, 520–529. [Google Scholar] [CrossRef]
- Holm, R.K.; Berg, N.I.; Walkusch, M.; Rasmussen, P.O.; Hansen, R.H. Design of a magnetic lead screw for wave energy conversion. IEEE Trans. Ind. Appl. 2013, 49, 2699–2708. [Google Scholar] [CrossRef]
- Datta, R.; Ranganathan, V.T. Variable-speed wind power generation using doubly fed wound rotor induction machine-a comparison with alternative schemes. IEEE Trans. Energy Convers. 2002, 17, 414–421. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; Martínez de Alegría, I.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Mohan, N. Advanced Electric Drives: Analysis, Control, and Modeling Using MATLAB/Simulink; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Ahmed, T.; Nishida, K.; Nakaoka, M. Grid power integration technologies for offshore ocean wave energy. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 2378–2385.
- Schlemmer, K.; Fuchshumer, F.; Böhmer, N.; Costello, R.; Villegas, C. Design and control of a hydraulic power take-off for an axi-symmetric heaving point absorber. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011.
- Sjolte, J.; Tjensvoll, G.; Molinas, M. Power collection from wave energy farms. Appl. Sci. 2013, 3, 420–436. [Google Scholar] [CrossRef]
- Zhou, Z.; Knapp, W.; MacEnri, J.; Sorensen, H.C.; Madsen, E.F.; Masters, I.; Igic, P. Permanent magnet generator control and electrical system configuration for Wave Dragon MW wave energy take-off system. In Proceedings of the IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 1580–1585.
- Sjolte, J.; Sandvik, C.M.; Tedeschi, E.; Molinas, M. Exploring the potential for increased production from the wave energy converter lifesaver by reactive control. Energies 2013, 6, 3706–3733. [Google Scholar] [CrossRef] [Green Version]
- Pan, C.T.; Liaw, J.H. A robust field-weakening control strategy for surface-mounted permanent-magnet motor drives. IEEE Trans. Energy Convers. 2005, 20, 701–709. [Google Scholar] [CrossRef]
- Jasinski, M.; Malinowski, M.; Kazmierkowski, M.P.; Sorensen, H.C.; Friis-Madsen, E.; Swierczynski, D. Control of AC/DC/AC converter for multi MW wave dragon offshore energy conversion system. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 2685–2690.
- Baker, N.J. Linear generators for direct drive marine renewable energy converters. Ph.D. Thesis, Durham University, Durham, UK, 2003. [Google Scholar]
- Danielsson, O.; Leijon, M.; Sjostedt, E. Detailed study of the magnetic circuit in a longitudinal flux permanent-magnet synchronous linear generator. IEEE Trans. Magn. 2005, 41, 2490–2495. [Google Scholar] [CrossRef]
- Danielsson, O. Wave Energy Conversion: Linear Synchronous Permanent Magnet Generator; Uppsala University: Uppsala, Sweden, 2006. [Google Scholar]
- Baker, N.J.; Mueller, M.; Spooner, E. Permanent magnet air-cored tubular linear generator for marine energy converters. In Proceedings of the Second International Conference on Power Electronics, Machines and Drives, Edinburgh, UK, 31 March–2 April 2004; Volume 2, pp. 862–867.
- Hodgins, N.; Keysan, O.; McDonald, A.S.; Mueller, M.A. Design and testing of a linear generator for wave-energy applications. IEEE Trans. Ind. Electron. 2012, 59, 2094–2103. [Google Scholar] [CrossRef]
- Polinder, H.; Damen, M.E.C.; Gardner, F. Linear PM Generator system for wave energy conversion in the AWS. IEEE Trans. Energy Convers. 2004, 19, 583–589. [Google Scholar] [CrossRef]
- Spooner, E.; Grimwade, C.J. SnapperTM: an efficient and compact direct electric power take-off device for wave energy converters. In Proceedings of the World Maritime Technology Conference, London, UK, 6–10 March 2006; pp. 6–10.
- Crozier, R.C. Optimisation and comparison of integrated models of direct-drive linear machines for wave energy conversion. Ph.D. Thesis, University of Edinburgh, Edinburgh, Scotland, 2014. [Google Scholar]
- Crozier, R.C.; Bailey, H.; Spooner, E.; McKeever, P.; Mueller, M.A. Analysis, design and testing of a novel direct-drive wave energy converter system. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011.
- Rasmussen, P.O.; Andersen, T.O.; Jorgensen, F.T.; Nielsen, O. Development of a high-performance magnetic gear. IEEE Trans. Ind. Appl. 2005, 41, 764–770. [Google Scholar] [CrossRef]
- Crozier, R.C.; Bailey, H.; Mueller, M.A.; Spooner, E.; McKeever, P. Analysis, design and testing of a novel direct-drive wave energy converter system. Renew. Power Gener. IET 2013, 7, 565–573. [Google Scholar] [CrossRef]
- McKeever, P.; Ng, C.; Caffrey, B.; Crozier, R.C.; Spooner, E. Snapper wave energy—The machine and grid interface system development. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011.
- Tamura, J. Calculation method of losses and efficiency of wind generators. In Wind Energy Conversion Systems; Springer: Berlin, Germany, 2012; pp. 25–51. [Google Scholar]
- Baroudi, J.A.; Dinavahi, V.; Knight, A.M. A review of power converter topologies for wind generators. In Proceedings of the 2005 IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15–18 May 2005; pp. 458–465.
- Hughes, A.; Drury, B. Electric Motors and Drives: Fundamentals, Types and Applications; Newnes: Burlington, MA, USA, 2013. [Google Scholar]
- Dos Santos, E.; da Silva, E.R. Advanced Power Electronics Converters: PWM Converters Processing AC Voltages; John Wiley & Sons: New York, NY, USA, 2014; Volume 46. [Google Scholar]
- Bai, H.; Wang, F.; Xing, J. Control strategy of combined PWM rectifier/inverter for a high speed generator power system. In Proceedings of the 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007; pp. 132–135.
- Khaburi, D.A.; Nazempour, A. Design and simulation of a PWM rectifier connected to a PM generator of micro turbine unit. Sci. Iran. 2012, 19, 820–828. [Google Scholar] [CrossRef]
- Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis-part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Trzynadlowski, A.M. A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives. IEEE Trans. Power Electron. 2003, 18, 1390–1396. [Google Scholar] [CrossRef]
- Kang, S.S. Advanced cooling for power electronics. In Proceedings of the 7th International Conference on Integrated Power Electronics Systems (CIPS), Nuremberg, Germany, 6–8 March 2012; pp. 1–8.
- Kumar, P.; Singh, A.K. Grid Codes: Goals and Challenges. In Renewable Energy Integration; Springer: Berlin, Germany, 2014; pp. 17–39. [Google Scholar]
- Distribution Code. Technical Report Version 4; Distribution System Operator ESB Networks Limited: Dublin, Ireland, April 2015. [Google Scholar]
- EirGrid Grid Code. Technical Report Version 6; EirGrid Group: Dublin, Ireland, July 2015. [Google Scholar]
- The Grid Code. Technical Report Issue 5; Revision 14; National Grid Electricity Transmission: Warwick, UK, August 2015. [Google Scholar]
- The Indian Electricity Grid Code. Technical Report L-1/18/2010-CERC; Central Electricity Regulatory Commission: New Delhi, India, 2010. [Google Scholar]
- Machado, I.; Arias, I. Grid Codes Comparison. Master’s Thesis, Department of ElectricPower Engineering, Chalmers University of Technology, Gothenburg, Sweden, 2006. [Google Scholar]
- Tissandier, J.; Babarit, A.; Clément, A.H. Study of the smoothing effect on the power production in an array of SEAREV wave energy converters. In Proceedings of the Eighteenth International Offshore and Polar Engineering Conference, Vancouver, BC, Canada, 6–11 July 2008.
- Comech, M.P.; García-Gracia, M.; Arroyo, S.M.; Guillén, M.Á.M. Wind farms and grid codes. In From Turbine to Wind Farms—Technical Requirements and Spin-Off Products; InTECH: Rijeka, Croatia, 2011; p. 17. [Google Scholar]
- Gashi, A.; Kabashi, G.; Kabashi, S.; Ahmetaj, S.; Veliu, V. Simulation the Wind Grid Code Requirements for Wind Farms Connection in Kosovo Transmission Grid. Energy Power Eng. 2012, 4, 25082. [Google Scholar] [CrossRef]
- Fryze, S. Wirk-, Blind-und Scheinleistung in elektrischen Stromkreisen mit nichtsinusförmigem Verlauf von Strom und Spannung. Elektrotech. Z. 1932, 53, 700–702. [Google Scholar]
- Martínez de Alegría, I.; Martín, J.L.; Kortabarria, I.; Andreu, J.; Ibañez Ereño, P. Transmission alternatives for offshore electrical power. Renew. Sustain. Energy Rev. 2009, 13, 1027–1038. [Google Scholar] [CrossRef]
- Sharkey, F.; Conlon, M.; Gaughan, K. Practical Analysis of Key Electrical Interfaces for Wave Energy Converter Arrays. In Proceedings of the 4th International Conference on Ocean Energy, Dublin, Ireland, 17–19 October 2012.

































| References | Hydrodynamic Model | Hydraulic Transmission | Electric Conversion | Grid Requirements | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cylinder | Valves | Accumulators | Motor | Electric Generator | Converter | |||||
| Fully Linear (Cummins) | Nonlinear Effects | Constraints | Losses | Losses | ||||||
| [8] | √ | × | Compressibility | × | adiabatic | × | × | × | ||
| [9] | √ | × | × | × | adiabatic | × | cte. T & | × | × | |
| [10] | √ | × | × | × | isothermal | cte. Pow. loss | dynamic | N/A | √ | |
| [11] | Viscous drag | × | × | × | adiabatic | √ | cte. T & | × | × | |
| [12] | NL restoring | × | × | × | √ | × | dynamic | N/A | √ | |
| [13] | √ | √ | √ | √ | √ | √ | Steady-state dynamics (NO transient) | map | × | |
| N/A | × | |||||||||
| [14] | √ | N/A | √ | √ | × | |||||
| [1] | √ | N/A | √ | √ | √ | |||||
| [15] | √ | N/A | dynamic | √ | ||||||
| [16] | √ | N/A | dynamic | × | ||||||
| Nominal Voltage | Normal Operating Ranges | |
|---|---|---|
| UK | Ireland | |
| 400 kV | 400 kV | 350–420 kV |
| 275 kV | 275 kV | 200–245 kV |
| 132 kV | 132 kV | 99–123 kV |
| Country | Frequency Range | Requirements |
|---|---|---|
| UK | 51.5–52 Hz | At least a period of 15 min of operation |
| 51–51.5 Hz | At least a period of 90 min of operation | |
| 49–51 Hz | Continuous operation | |
| 47.5–49 Hz | At least a period of 90 min of operation | |
| 47–47.5 Hz | At least a period of 20 s of operation | |
| Ireland | 49.5–50.5 Hz | Continuous operation |
| 47.5–52 Hz | Remain connected for a period of 60 min. | |
| 47–47.5 Hz | Remain connected for a period of 20 s | |
| above 50.2 Hz | No extra wind turbine shall be connected |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penalba, M.; Ringwood, J.V. A Review of Wave-to-Wire Models for Wave Energy Converters. Energies 2016, 9, 506. https://doi.org/10.3390/en9070506
Penalba M, Ringwood JV. A Review of Wave-to-Wire Models for Wave Energy Converters. Energies. 2016; 9(7):506. https://doi.org/10.3390/en9070506
Chicago/Turabian StylePenalba, Markel, and John V. Ringwood. 2016. "A Review of Wave-to-Wire Models for Wave Energy Converters" Energies 9, no. 7: 506. https://doi.org/10.3390/en9070506
APA StylePenalba, M., & Ringwood, J. V. (2016). A Review of Wave-to-Wire Models for Wave Energy Converters. Energies, 9(7), 506. https://doi.org/10.3390/en9070506