New Electro-Thermal Battery Pack Model of an Electric Vehicle
Abstract
:1. Introduction
2. Existing Battery Models
3. Overview of Selected Dynamic Battery Models
3.1. Tremblay Battery Model (Battery Model 1)
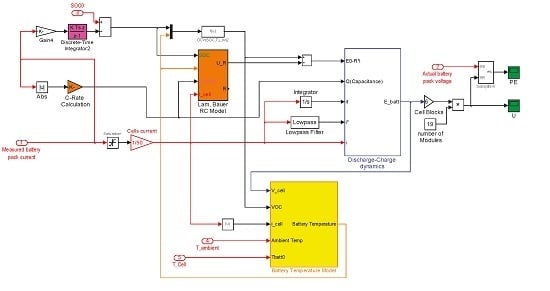
3.2. Lam and Bauer Battery Model (Battery Model 2)
3.3. Wijewardana Battery Model
3.4. Assessment of Battery Models Qualities
4. Battery Thermal Model
5. Experimental Characterization of the Battery and the Vehicle under the Test
5.1. Battery Measurements
5.2. Driving Tests on the Real Vehicle
6. Battery Models Validation
6.1. Evaluating the Open Circuit Voltage Models (VOC)
6.2. Evaluating the Battery Models Output Voltage
6.3. The Proposed Synthesized Battery Model
7. Conclusions
Author Contributions
Conflicts of Interest
Appendix
Appendix A.1. Nomenclature
| Parameter (Unit) | Symbol | Value |
|---|---|---|
| Constant voltage (V) | E0 | 3.21 [23] |
| Constant internal resistance (Ω) | R | 0.0833 |
| Polarization constant (V/(Ah)) or polarization resistance (Ω) | K | 0.0119 [23] |
| Battery capacity (Ah) | Q | Variable |
| Actual battery charge (Ah) | it | Variable |
| Exponential zone amplitude (V) | A | 0.2711 [23] |
| Exponential zone time constant inverse (Ah)−1 | B | 152.130 [23] |
| Battery current (A) | i | Variable |
| Filtered current (A) | i* | Variable |
| Voltage change due to electrolyte electrons transfer formation | ΔVChe | Variable |
| the effective voltage gradient | dVChe/dT | 0.0016 [1] |
| Constant property of electrolyte | CChe | 0.07 [1] |
| Constant property of electrolyte | CChe1 | 0.001 [1] |
| Constant property of electrolyte | b | 0.0012 [1] |
| Constant property of electrolyte | w | 0.012 [1] |
| Voltage change due to electrode film formation | ΔE | Variable |
| voltage gradient | dVr/dT | 0.00003 [1] |
| Constant property | CE1 | 0.00011 [1] |
| Battery module surface area (m2) | A | 0.283954 |
| Battery cell mass (kg) | m | 0.04 [23] |
| Battery module mass (kg) | M | 12 |
| Specific heat capacity (J·kg−1·K−1) | Cp | 1360 [27] |
| Stefane-Boltzmann constant (W·m−2·K4) | σ | 5.67 × 10−8 |
| Emissivity of heat | ε | 0.95 |
| Natural heat convection constant (W·m−2·K−1) | h | 4 |
Appendix A.2. Driving Tests


Appendix A.3. The Vehicle under the Test

| Parameter | Value |
|---|---|
| Rated Power, PN | 45 kW |
| Peak Power, Pmax | 68 kW |
| Peak Torque, Tmax | 210 N·m |
| Rated Speed, nN | 3000 rpm |

References
- Wijewardana, S.; Vepa, R.; Shaheed, M.H. Dynamic battery cell model and state of charge estimation. J. Power Sources 2016, 308, 109–120. [Google Scholar] [CrossRef]
- Doppebattery Model 2auer, M. Hybrid and Electric Vehicles—Lecture Notes; ETI-HEV, Karlsruhe Institute of Technology: Karlsruhe, Germany, 2014.
- Ivers-Tiffee, E. Batteries and Fuel Cells—Lecture Notes; IWE, Karlsruhe Institute of Technology: Karlsruhe, Germany, 2012. [Google Scholar]
- Illig, J. Physically Based Impedance Modelling of Lithium-Ion Cells. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2014. [Google Scholar]
- Tremblay, O.; Dessaint, L.-A. Experimental validation of a battery dynamic model for EV applications. World Electr. Veh. J. 2009, 3, 1–10. [Google Scholar]
- Padhi, A.K.; Nanjundaswamy, K.S.; Goodenough, J.B.D. Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 1997, 144, 1188–1194. [Google Scholar] [CrossRef]
- Valence Technology. U-Charge® XP Rev 2 User Manual; Valence Technology, Inc.: Austin, TX, USA, 2011. [Google Scholar]
- Lin, N.; Ci, S.; Li, H. An enhanced circuit-based battery model with considerations of temperature effect. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 3985–3989.
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Dees, D.W.; Battaglia, V.S.; Bélanger, A. Electrochemical modeling of lithium polymer batteries. J. Power Sources 2002, 110, 310–320. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Hussein, A.A.; Batarseh, I. An overview of generic battery models. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–6.
- Kroeze, R.C.; Krein, P.T. Electrical battery model for use in dynamic electric vehicle simulations. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1336–1342.
- Liu, X.; Ma, Y.; Ying, Z. Research of SOC estimation for lithium-ion battery of electric vehicle based on AMEsim-simulink co-simulation. In Proceedings of the 32nd Chinese Control Conference (CCC), Xi’an, China, 26–28 July 2013; pp. 7680–7685.
- Szumanowski, A.; Chang, Y. Battery management system based on battery nonlinear dynamics modeling. IEEE Trans. Veh. Technol. 2008, 57, 1425–1432. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, W.; Sharkh, S.M. Estimation of state of charge of lithium-ion batteries used in HEV using robust extended Kalman filtering. Energies 2012, 5, 1098–1115. [Google Scholar] [CrossRef]
- Watrin, N.; Roche, R.; Ostermann, H.; Blunier, B.; Miraoui, A. Multiphysical lithium-based battery model for use in state-of-charge determination. IEEE Trans. Veh. Technol. 2012, 61, 3420–3429. [Google Scholar] [CrossRef]
- Lam, L.; Bauer, P.; Kelder, E. A practical circuit-based model for Li-ion battery cells in electric vehicle applications. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, The Netherlands, 9–13 October 2011; pp. 1–9.
- Tremblay, O.; Dessaint, L.A.; Dekkiche, A.I. A generic battery model for the dynamic simulation of hybrid electric vehicles. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 284–289.
- Shepherd, C.M. Design of primary and secondary cells II. An equation describing battery discharge. J. Electrochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Saw, L.H.; Somasundaram, K.; Ye, Y.; Tay, A.A.O. Electro-thermal analysis of Lithium Iron Phosphate battery for electric vehicles. J. Power Sources 2014, 249, 231–238. [Google Scholar] [CrossRef]
- Tan, Y.K.; Mao, J.C.; Tseng, K.G. Modelling of battery temperature effect on electrical characteristics of Li-ion battery in hybrid electric vehicle. In Proceedings of the 2011 IEEE Ninth International Conference on Power Electronics and Drive Systems (PEDS), Singapore, Singapore, 5–8 December 2011.
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Kim, Y.; Siegel, J.B.; Stefanopoulou, A.G. A computationally efficient thermal model of cylindrical battery cells for the estimation of radially distributed temperatures. In Proceedings of the 2013 American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013; pp. 698–703.
- Rad, M.S.; Danilov, D.L.; Baghalha, M.; Kazemeini, M.; Notten, P.H. Thermal modeling of cylindrical LiFeMgPO4 Batteries. J. Mod. Phys. 2013, 4, 1–7. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M.; Pesaran, A.A. A parametric study on thermal management of an air-cooled lithium-ion battery module for plug-in hybrid electric vehicles. J. Power Sources 2013, 238, 301–312. [Google Scholar] [CrossRef]
- Sun, Y. Construction and Validation of a Thermal FEM-Model of an Automobile Battery. Master’s Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2011. [Google Scholar]
- Gießler, M.; Fritz, A.; Paul, J.; Sander, O.; Gauterin, F.; Müller-Glaser, K.D. Converted vehicle for battery electric drive: Aspects on the design of the software-driven vehicle control unit. In Proceedings of the 2nd International Energy Efficient Vehicle Conference (EEVC), Dresden, Germany, 18–19 June 2012.
- Blank, T.; Lipps, C.; Ott, W.; Hoffmann, P.; Weber, M. Influence of environmental conditions on the sensing accuracy of Li-Ion battery management systems with passive charge balancing. In Proceedings of the 17th European Conference on Power Electronics and Applications, Geneva, Switzerland, 8–10 September 2015; pp. 1–9.













| Parameter (Unit) | Value |
|---|---|
| Nominal Module Voltage (V) | 19.2 |
| Nominal Module Capacity (Ah) | 69 |
| Max Continuous Load Current (A) | 120 |
| Peak Current for 30 s (A) | 200 |
| Feature | Battery Model 1 | Battery Model 2 | Battery Model 3 | |||
|---|---|---|---|---|---|---|
| Charge-Discharge hysteresis | ++ | Considered in the output voltage | + | Considered in the internal resistance (R) equations | - | Charge-discharge |
| Open circuit voltage | - | Constant value for E0 | + | VOC(SOC) | + | VOC(SOC) |
| Internal resistance (R) | - | Constant value | ++ | R(SOC,T,C-rate) | + | R(SOC,T) |
| Temperature influence | - | Not considered | + | Considered in the internal resistance model | + | Considered as potential correction terms |
| Capacity fading | - | Not considered | + | Considered in the battery’s used capacity estimation | + | Considered in the battery’s internal resistance (R) estimation |
| Total Assessment | 2 | 6 | 4 | |||
| Constant | Value | Constant | Value |
|---|---|---|---|
| a1 | −1.166 | b1 | −0.9135 |
| a2 | −35 | b2 | −35 |
| a3 | 3.344 | b3 | 3.484 |
| a4 | 0.1102 | b4 | 0.1102 |
| a5 | −0.1718 | b5 | −0.1718 |
| a6 | −2 × 10−3 | b6 | −8 × 10−3 |
| dVOC,d/dT | 0.00125 | dVOC,c/dT | 0.00069 |
| Temperature °C | MSE in Discharge Model % | MSE in Charge Model % |
|---|---|---|
| 10 | 0.5232 | 0.8914 |
| 20 | 0.5320 | 0.5719 |
| 40 | 0.5751 | 0.4522 |
| Constant | Value | Constant | Value | Constant | Value | Constant | Value |
|---|---|---|---|---|---|---|---|
| c1 | 1.080 × 10−2 | c11 | −6.580 | c21 | −6.919 × 10−1 | c31 | −2.398 × 103 |
| c2 | −11.03 | c12 | 12.11 | c22 | 2.902 × 10−1 | c32 | 1.298 × 10−1 |
| c3 | 1.827 × 10−2 | c13 | 2.950 × 10−1 | c23 | 2.130 × 106 | c33 | −2.892 × 10−1 |
| c4 | −6.462 × 10−3 | c14 | −20.00 | c24 | −6.007 × 106 | c34 | 2.273 × 10−1 |
| c5 | −3.697 × 10−4 | c15 | 4.722 × 10−2 | c25 | 6.271 × 106 | c35 | −7.216 × 10−2 |
| c6 | 2.225 × 10−4 | c16 | −2.420 × 10−2 | c26 | −2.958 × 106 | c36 | 8.980 × 10−2 |
| c7 | 1.697 × 102 | c17 | 6.718 × 10−3 | c27 | 5.998 × 105 | c37 | 7.613 × 10−1 |
| c8 | −1.007 × 103 | c18 | −20.00 | c28 | −3.102 × 104 | c38 | 10.14 |
| c9 | 1.408 × 103 | c19 | −5.967 × 10−4 | c29 | 2.232 × 103 | c39 | 2.608 × 102 |
| c10 | 3.897 × 102 | c20 | 6.993 × 10−1 | c30 | 3.128 × 103 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhanouti, M.; Gießler, M.; Blank, T.; Gauterin, F. New Electro-Thermal Battery Pack Model of an Electric Vehicle. Energies 2016, 9, 563. https://doi.org/10.3390/en9070563
Alhanouti M, Gießler M, Blank T, Gauterin F. New Electro-Thermal Battery Pack Model of an Electric Vehicle. Energies. 2016; 9(7):563. https://doi.org/10.3390/en9070563
Chicago/Turabian StyleAlhanouti, Muhammed, Martin Gießler, Thomas Blank, and Frank Gauterin. 2016. "New Electro-Thermal Battery Pack Model of an Electric Vehicle" Energies 9, no. 7: 563. https://doi.org/10.3390/en9070563
APA StyleAlhanouti, M., Gießler, M., Blank, T., & Gauterin, F. (2016). New Electro-Thermal Battery Pack Model of an Electric Vehicle. Energies, 9(7), 563. https://doi.org/10.3390/en9070563