Analytical Calculation of D- and Q-axis Inductance for Interior Permanent Magnet Motors Based on Winding Function Theory

Abstract

Interior permanent magnet (IPM) motors are widely used in electric vehicles (EVs), benefiting from the excellent advantages of a more rational use of energy. For further improvement of energy utilization, this paper presents an analytical method of d- and q-axis inductance calculation for IPM motors with V-shaped rotor in no-load condition. A lumped parameter magnetic circuit model (LPMCM) is adopted to investigate the saturation and nonlinearity of the bridge. Taking into account the influence of magnetic field distribution on inductance, the winding function theory (WFT) is employed to accurately calculate the armature reaction airgap magnetic field and d- and q-axis inductances. The validity of the analytical technique is verified by the finite element method (FEM).

1. Introduction

In recent decades, permanent magnet (PM) motors cover a wide range of industrial applications, especially for electric vehicles (EVs), attributing to the compact structure, high efficiency, high power/torque density and excellent dynamic performances [1,2,3,4,5,6]. As a typical topology of PM motors, the interior permanent magnet (IPM) motors with a V-shape provide a more superior performance of the flux-weakening capability and wider constant-power speed range [7,8,9,10], achieving considerable attention. Along with these excellent advantages, IPM motors offer a great alternative opportunity to contribute for a more rational use of energy, which makes EVs have the potential to provide a perfect solution to energy security and environmental impacts in the future [11,12].

The d- and q-axis inductances are key parameters for the performance design including flux-weakening capability, power factor and control strategy [13,14,15]. For the first stage of the IPM motor design, the calculation of d- and q-axis inductances in no-load condition is crucial.

For IPM motors, on one hand, the magnetic bridges protect the permanent magnets from flying away from the rotor. On the other hand, they provide a path for the permanent-magnet leakage flux and cause saturation. The influence of magnetic bridge saturation is the biggest obstacle for the calculation of d- and q-axis inductances. In addition, the accurate paths of d- and q-axis fluxes are another crucial point.

Various researches on inductance with finite element method (FEM) have been successfully investigated in the past [16], e.g., a 3D FEM model is used to calculate the inductances considering the end effect and magnetic flux leakage [17]. In [18], taking into account saturation and nonlinearity, the cross-coupling inductance characteristics are investigated. FEM can effectively analyze the inductances accounting for the saturation, nonlinearity, complex geometry and cross-coupling influence. However, FEM is too theory-lacking and time-consuming to provide a physical insight to the motor design, especially for the influence of parameter variation at the first stages of the design process.

Comparatively speaking, analytical methods are often preferred. Lumped parameter magnetic circuit model (LPMCM) is a common method. In [19,20], the d- and q-axis inductances are calculated with LPMCMs, which are established based on the d- and q-axis flux paths matching the practical operating point of the control issue. The influence of saturation and nonlinearity is analyzed. In [21], the motor is divided into several mechanical phase regions according to the winding distribution. On the basis of the mechanical phase region and equivalent magnetic circuit, the d- and q-axis inductances are predicted. Although LPMCM has advantages in saturation and nonlinearity, the drawback of the method is that the calculation accuracy is greatly affected by the way flux paths are divided and analytical models are built. On the other hand, though the LPMCM expresses the relationship of permeance, it is complicated to classify the permeance according to their contributions. Especially for the motor with distributed winding, the amount of teeth is too much, which makes it more difficult to classify the flux paths and calculate the inductance based on permeance. Furthermore, the accurate flux used for the inductance calculation is the summation of the main and leakage magnetic field. However, the LPMCM calculates the main permeance, neglecting the influence of leakage permeance, which is what causes calculation error.

This paper presents an analytical method for d- and q-axis inductance calculation in no-load condition based on LPMCM and winding function theory (WFT). LPMCM is adapted to the calculation of magnetic bridge saturation, and WFT is employed to divide accurate paths of d- and q-axis fluxes and consider the influence of magnetic field distribution. The d- and q-axis flux linkages produced by a very small current are calculated, based on which d- and q-axis inductances can be obtained. The FEM results verify the validity of the proposed method.

2. Analytical Method

A 48-slot/8-pole IPM motor with a V-shaped rotor is instanced to verify the proposed method. Figure 1 shows the model with magnetic bridges, where α is the magnet pole-arc to pole-pitch ratio, β is the barrier arc to pole-pitch ratio, R_s is the stator bore radius, R_r is the rotor outer radius, t_b is the bridge thickness, w_bar is the barrier width, l_bar1 and l_bar2 are the barrier length, w_m is the PM width, l_m is the PM length in magnetization direction, w_r is the rib width, l_r is the rib length. For IPM motors, the saturation mainly focuses on the bridge. Here, we assume that the permeability of stator and rotor (except the bridge) core is infinite.

2.1. Saturation Calculation

The leakage fluxes pass the bridges causing different saturation characteristics depending on the rotor shape. For the sake of simplicity, the rotor is divided into two pieces: saturation regions with a constant permeability and non-saturation region with infinite permeability shown in Figure 2. The saturation regions of bridges are widened, where the equivalent bridge width can be expressed as

$$w_b=w_{bar}+2t_b$$

(1)

As shown in Figure 3, the fluxes, produced by magnets, pass the magnet, magnetic bridges, and air-gap. Considering the flux paths around the magnets, an LPMCM is employed to analyze the saturation and nonlinearity of bridges. Figure 4 depicts the LPMCM of one-half of two magnets with opposite poles and the associated bridges behind the magnet halves, where R_m is the reluctance of magnet, R_g is the reluctance of one-half of the per pole air gap, R_b is the reluctance of bridge, Φ_r, Φ₀, Φ_g and Φ_b are the remanent magnet flux, magnet leakage flux, air-gap flux and bridge leakage flux, respectively.

In the LPMCM, the permeability of bridge is a nonlinear uncertain parameter, which is the basic of the solution for the all fluxes. The iterative method is effective for this problem. Figure 5 shows the iterative process:

• Firstly, the initial flux density of bridge is supposed as B_b.
• Secondly, calculate all the reluctances and fluxes according to the material B–H profile and the law of magnetic flux continuity.
• Thirdly, compare the obtained flux density of bridge B_b1 with B_b.
• Finally, adjust B_b and repeat this process until the error is satisfied.

All the parameters can be expressed as:

$$R_m=\frac{l_m}{{\mu }_0{\mu }_r{w}_{m}L}$$

(2)

$$R_g=\frac{R_s-R_r}{{\mu }_0\frac{\left(R_s+R_r\right)}{2}\frac{2\pi }{4p}L}$$

(3)

$$R_b=\frac{w_b}{\mu \left(B_b\right)\cdot t_{b}L}$$

(4)

$${\varphi }_r=B_r{w}_{m}L$$

(5)

$${\varphi }_b=\frac{R_m{R}_g}{R_m{R}_b+R_b{R}_g+R_g{R}_m}{\varphi }_r$$

(6)

$$B_{b1}=\frac{{\varphi }_b}{t_{b}L}$$

(7)

where L is effective length of the rotor and stator, B_r is the remanence of magnet, p is the number of pole pairs, μ_r is the relative permeability of magnet, μ₀ and μ (B_b) are the permeability of air and bridge, respectively.

2.2. Inductance Calculation

When the current is very small, the influence of armature-reaction magnetic field on saturation can be neglected, and the d- and q-axis inductances in no-load condition are obtained by:

$$\{\begin{array}{l}{L}_d=\frac{{\varphi }_d}{I_d}+L_0\\ L_q=\frac{{\varphi }_q}{I_q}+L_0\end{array}$$

(8)

where φ_d and φ_q are the main flux linkages in d- and q-axis, I_d and I_q are the currents in d- and q-axis, respectively. L₀ is the leakage inductance.

Taking into account the influence of magnetic field distribution, the WFT is used to accurately calculate the d- and q-axis inductances. For the clear expression of magnetic motive force (MMF) and rotor magnetic potential, the initial condition is that all the angular positions are expressed with electrical degree.

Based on the winding function, the armature-reaction MMF of each phase can be expanded into a Fourier series as [22,23]:

$$\{\begin{array}{l}{F}_a={\displaystyle \sum _{\nu }\frac{2N{k}_{wv}I}{vp\pi }}\cos \left(\nu {\theta }_s\right)\cos \left(\omega t+\phi \right)\\ F_b={\displaystyle \sum _{\nu }\frac{2N{k}_{wv}I}{vp\pi }}\cos \left(\nu \left({\theta }_s-\frac{2\pi }{3}\right)\right)\cos \left(\omega t+\phi -\frac{2\pi }{3}\right)\\ F_c={\displaystyle \sum _{\nu }\frac{2N{k}_{wv}I}{vp\pi }}\cos \left(\nu \left({\theta }_s-\frac{4\pi }{3}\right)\right)\cos \left(\omega t+\phi -\frac{4\pi }{3}\right)\end{array}$$

(9)

where N is the amount of winding turns in series of stator phase, k_wv is the winding factor, I is the amplitude of phase current, ϕ is the current phase measured from the a-axis, ω is the rated electrical angular velocity, and θ_s is the angular position in the stator reference frame measured from the axis of phase a shown in Figure 6.

The synthetic armature-reaction MMF is obtained by:

$$\begin{array}{l}{F}_s({\theta }_s,t)=F_a+F_b+F_c\\ ={\displaystyle \sum _{v}F}\cos (v{\theta }_s+k_v(\omega t+\phi ))\end{array}$$

(10)

where

$$\{\begin{array}{l}F=3\frac{N{k}_{wv}}{vp\pi }I\\ k_v=-1,forv=6(m-1)+1\\ k_v=1,forv=6m-1\\ m=1,2,\mathrm{3...}\end{array}$$

(11)

2.2.1. D-Axis Magnetic Potential

When ϕ = 0, t = 0 and the d-axis overlaps with the a-axis, the flux passes the d-axis path shown in Figure 7.

As the permeability of the non-saturation region in rotor is much larger than that of the magnet and barrier, the magnet and barrier can be regarded as equal-potential area. The magnetic potential distribution of the rotor in the d-axis is shown in Figure 8. In one-half of the electrical period, the rotor magnetic potential can be expressed as

$$F_d({\theta }_s)=U_{d1}\frac{4}{\pi }{\displaystyle \sum _j\frac{\sin \left(j\frac{\alpha \pi }{2}\right)}{j}}\cos \left(j{\theta }_s\right)+U_{d2}\frac{4}{\pi }{\displaystyle \sum _j\frac{\sin \left(j\frac{\beta \pi }{2}\right)-\sin \left(j\frac{\alpha \pi }{2}\right)}{j}}\cos \left(j{\theta }_s\right)$$

(12)

where U_d1 and U_d2 are the magnetic potentials shown in Figure 7.

According to the continuity of magnetic flux, the flux through the air-gap is equal to that passing the rotor. The path of the d-axis flux in the rotor consists of the magnet, barrier and bridge. Based on the path, the fluxes in the rotor can be calculated by

$$\{\begin{array}{l}{\displaystyle {\int }_{-\frac{\alpha \pi }{2}}^{\frac{\alpha \pi }{2}}(F_s({\theta }_s,0)-F_d({\theta }_s))\frac{{\mu }_0}{p\left(R_s-R_r\right)}\frac{R_s+R_r}{2}Ld{\theta }_s}=U_{d1}\left(\frac{2{\mu }_0{\mu }_r{w}_{m}L}{l_m}+\frac{2{\mu }_0\left(l_{bar1}+l_{bar2}\right)L}{w_{bar}}+\frac{2{\mu }_0\mu \left(B_b\right)t_{b}L}{w_b}\right)\\ {\displaystyle {\int }_{\frac{\alpha \pi }{2}}^{\frac{\beta \pi }{2}}(F_s({\theta }_s,0)-F_d({\theta }_s))\frac{{\mu }_0}{p\left(R_s-R_r\right)}\frac{R_s+R_r}{2}Ld{\theta }_s}=U_{d2}\frac{{\mu }_0\mu \left(B_b\right)t_{b}L}{w_b}\end{array}$$

(13)

Substituting (10) and (12) into (13), the magnetic potentials can be obtained as:

$$\{\begin{array}{l}{U}_{d1}={\displaystyle \sum _v\frac{2F{P}_1\sin \left(\frac{v\alpha \pi }{2}\right)}{v\left(P_2+P_3+P_4+P_5\right)}}\\ U_{d2}={\displaystyle \sum _v\frac{F{P}_1\left(\sin \left(\frac{v\beta \pi }{2}\right)-sin\left(\frac{v\alpha \pi }{2}\right)\right)}{v\left(0.5P_5+P_6\right)}}\end{array}$$

(14)

where

$$P_1=\frac{{\mu }_0}{p\left(R_s-R_r\right)}\frac{R_s+R_r}{2}L$$

(15)

$$P_2=\frac{{\mu }_0}{p\left(R_s-R_r\right)}\frac{R_s+R_r}{2}L\alpha \pi$$

(16)

$$P_3=\frac{2{\mu }_0{\mu }_r{w}_{m}L}{l_m}$$

(17)

$$P_4=\frac{2{\mu }_0\left(l_{bar1}+l_{bar2}\right)L}{w_{bar}}$$

(18)

$$P_5=\frac{2{\mu }_0\mu \left(B_b\right)t_{b}L}{w_b}$$

(19)

$$P_6=\frac{{\mu }_0}{p\left(R_s-R_r\right)}\frac{R_s+R_r}{2}L\frac{\left(\beta -\alpha \right)\pi }{2}$$

(20)

2.2.2. Q-Axis Magnetic Potential

When ϕ = 0, t = 0 and the q-axis overlaps with the a-axis, the flux passes the q-axis path shown in Figure 9. Similarly, the magnetic potential distribution of rotor in the q-axis is shown in Figure 10, and can be expressed in a Fourier series as

$$F_q({\theta }_s)=U_q\frac{4}{\pi }{\displaystyle \sum _j\frac{\sin \left(j\frac{\left(1-\alpha \right)\pi }{2}\right)-\sin \left(j\frac{\left(1-\beta \right)\pi }{2}\right)}{j}}\cos \left(j{\theta }_s\right)$$

(21)

where U_q is the magnetic potential shown in Figure 9.

As shown in Figure 9, the flux is divided into two parts in bridge region. The two parts operate in parallel, and the length of each path is 0.5 w_b. The flux in the q-axis can be calculated by

$${\displaystyle {\int }_{\frac{\left(1-\beta \right)\pi }{2}}^{\frac{\left(1-\alpha \right)\pi }{2}}\left(F_s\left({\theta }_s,0\right)-F_q\left({\theta }_s\right)\right)\frac{{\mu }_0}{p\left(R_s-R_r\right)}\frac{R_s+R_r}{2}Ld{\theta }_s}=U_q\left(\frac{{\mu }_0\mu \left(B_b\right)t_{b}L}{0.5w_b}+\frac{{\mu }_0\mu \left(B_b\right)t_{b}L}{0.5w_b}\right)$$

(22)

From Equation (17), we can get

$$U_q={\displaystyle \sum _v\frac{F{P}_1\left(\sin \left(\frac{v\left(1-\alpha \right)\pi }{2}\right)-sin\left(\frac{v\left(1-\beta \right)\pi }{2}\right)\right)}{v\left(2P_5+P_6\right)}}$$

(23)

2.2.3. D-and Q-Axis Inductances

The armature reaction airgap magnetic fields in d-axis can be obtained by

$$\begin{array}{l}{B}_d=\left(F_s\left({\theta }_s,0\right)-F_d\left({\theta }_s\right)\right)\frac{{\mu }_0}{\left(R_s-R_r\right)}\\ =\left({\displaystyle \sum _{v}F}\cos \left(v{\theta }_s\right)-U_{d1}\frac{4}{\pi }{\displaystyle \sum _j\frac{\sin \left(j\frac{\alpha \pi }{2}\right)}{j}}\cos (j{\theta }_s)-U_{d2}\frac{4}{\pi }{\displaystyle \sum _j\frac{\sin \left(j\frac{\beta \pi }{2}\right)-\sin \left(j\frac{\alpha \pi }{2}\right)}{j}}\cos (j{\theta }_s)\right)\frac{{\mu }_0}{\left(R_s-R_r\right)}\end{array}$$

(24)

The d-axis inductance can be calculated by

$$\{\begin{array}{l}{L}_d=L_{md}+L_0\\ L_{md}=\frac{{\displaystyle {\int }_0^{2\pi }{\displaystyle \sum _{\nu }\frac{2N{k}_{wv}}{vp\pi }}\cos \left(\nu {\theta }_s\right)B_d\frac{R_s+R_r}{2}Ld{\theta }_r}}{I}\end{array}$$

(25)

where L_md is the main inductance in the d-axis. L₀ consists of end-winding leakage inductance, slot leakage inductance and tooth-tip leakage inductance. The detailed computation processes of the leakage inductance are expressed in [24]. The end-winding leakage inductance can be calculated by

$$L_{ew}={\mu }_0{N}^{2}q\left(2l_w{\lambda }_h+w_{ew}{\lambda }_w\right)\frac{4m}{Q}$$

(26)

where q is the number of stator slots per pole and phase, l_w is the average length of the end winding, m is the number of phases, Q is the number of slots, w_ew is the coil span, λ_h is the empirical axial permeance factor and λ_w is the empirical span permeance factor of the end winding.

The slot leakage inductance is

$$L_u={\mu }_0{N}^{2}L\frac{4m}{Q}{\lambda }_u$$

(27)

where λ_w is the slot leakage permeance factor, which is relative to slot dimensions [13,24].

The tooth-tip leakage inductance is

$$L_{tt}={\mu }_0{N}^{2}L\frac{4m}{Q}{k}_{tt}{\lambda }_{tt}$$

(28)

where λ_tt is the tooth-tip leakage permeance factor, and k_tt is a factor that takes into account the presence of different phases in a slot [24].

The armature reaction airgap magnetic fields in the q-axis can be obtained by

$$\begin{array}{l}{B}_q=\left(F_s\left({\theta }_s,0\right)-F_q\left({\theta }_s\right)\right)\frac{{\mu }_0}{\left(R_s-R_r\right)}\\ =\left({\displaystyle \sum _{v}F}\cos \left(v{\theta }_s\right)-U_q\frac{4}{\pi }{\displaystyle \sum _j\frac{\sin \left(j\frac{\left(1-\alpha \right)\pi }{2}\right)-\sin \left(j\frac{\left(1-\beta \right)\pi }{2}\right)}{j}}\cos \left(j{\theta }_s\right)\right)\frac{{\mu }_0}{\left(R_s-R_r\right)}\end{array}$$

(29)

The q-axis inductance can be calculated by

$$\{\begin{array}{l}{L}_q=L_{mq}+L_0\\ L_{mq}=\frac{{\displaystyle {\int }_0^{2\pi }{\displaystyle \sum _{\nu }\frac{2N{k}_{wv}}{vp\pi }}\cos \left(\nu {\theta }_s\right)B_q\frac{R_s+R_r}{2}Ld{\theta }_r}}{I}\end{array}$$

(30)

where L_mq is the main inductance in the q-axis.

3. Results and Analysis

The armature reaction airgap magnetic fields and inductances in the d- and q-axis are calculated by the proposed method, and the validity is verified by FEM. The FEM results are obtained by the commercial software ANSYS (version 16.0, ANSYS, Pittsburgh, PA, USA). The main parameters of the motors are listed in

Table 1. Main parameters of the 8-pole/48-slot motor.

Symbol	Parameter	Results and Unit
p	Number of pole pairs	4
Q	Number of slots	48
I	Amplitude of phase current	1A
N	Amount of winding turns in series of stator phase	32
Br	Remanence of magnet	1.25
μr	Relative permeability of magnet	1.024
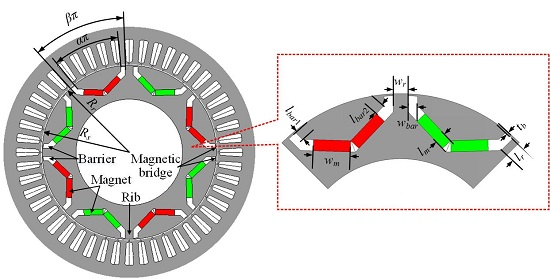
α	Magnet pole-arc to pole-pitch ratio	0.742
β	Barrier arc to pole-pitch ratio	0.886
Rs	Stator bore radius	91 mm
Rr	Rotor outer radius	90 mm
tb	Bridge thickness	1 mm
wbar	Barrier width	5 mm
lbar1	Barrier 1 length	5 mm
lbar2	Barrier 2 length	5.9 mm
wm	PM width	20 mm
lm	PM length in magnetization direction	6 mm
wr	Rib width	8 mm
lr	Rib length	8.8 mm

. Based on these parameters, the saturation of bridge is firstly investigated.

Table 2. Permeability of bridge.

Method	Value	Unit
Proposed method	4.40 × 10−5	H/m
Finite element method (FEM)	4.52 × 10−5	H/m

depicts the results of the analytical method and FEM. The comparison shows that the proposed method is very effective for bridge saturation.

Taking into account the influence of the armature-reaction magnetic field on saturation, a very small current is employed to calculate no-load d- and q-axis inductances. Freeze permeability is adopted to calculate the armature-reaction magnetic field. Figure 11 shows the waveforms of airgap flux density in the d- and q-axes. It is observed that the analytical results match well with that of FEM. Based on Equations (25) and (30), the d- and q-axis inductances in the no-load condition can be obtained shown in

Table 3. The inductances of the two methods.

Item	Proposed Method	FEM	Unit
D-axis inductance	0.524	0.513	mH
Q-axis inductance	1.267	1.271	mH

. The analytical data and simulation data tally well, which indicates that the proposed method is quite accurate for d- and q-axis inductance calculations.

4. Conclusions

In this paper, a novel analytical method of d- and q-axis inductance calculation in a no-load condition is proposed and applied to IPM motors with V-shaped rotors. Taking bridge saturation into consideration, the rotor is divided into two pieces: saturation regions with a constant permeability and non-saturation regions with infinite permeability. The LPMCM and iterative method effectively solve the saturation and nonlinearity of the bridge. The rotor magnetic potentials in the d- and q-axis are investigated according to the flux paths. Based on the WFT, the influence of magnetic field distribution on inductance is considered. The analytical results of bridge permeability, armature-reaction magnetic field and d- and q-axis inductances match well with the ones obtained by FEM, which confirms the validity of the proposed model.