Dispatching of Wind/Battery Energy Storage Hybrid Systems Using Inner Point Method-Based Model Predictive Control
Abstract
:1. Introduction
2. The Wind/Battery Energy Storage Hybrid System Modeling
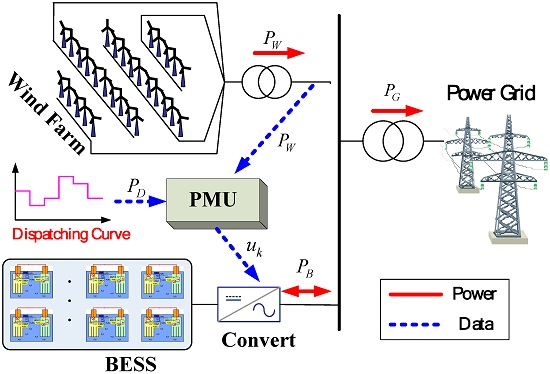
2.1. System Configuration
2.2. System Modeling
3. Dispatching Strategy for Wind/Battery Energy Storage Hybrid System Based on MPC
3.1. Wind Power Predicting and Dispatch Curve
3.2. Design for MPC Contoller for Dispatching
3.3. Rolling Optimization Using Inner Point Method
- Step 1: Select the initial condition (x(0), s(0), z(0)) satisfying s(0) > 0, z(0) > 0.
- Step 2: Obtain the Δu and Δz satisfying the following equation:where:
- Step 3: Update the variable through increment.
- Step 4: Judge the convergence. If it converges, the procedure would stop and the optimal control values are obtained, otherwise, the value are treated as initial value and sent into step 2 to solve iteratively.
4. Simulation Results
4.1. Capacity of BESS in 4.5 MWh
4.2. Capacity of BESS in 9 MWh
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Symbol | Description |
| PG/x1 | Total output of the wind/battery energy storage hybrid system |
| PB/u | The action of the BESS/control value |
| PW/d | Actual wind power/disturbance |
| EB/x2 | The remaining energy in a BESS |
| SOC | State of Charge of a BESS |
| ΔTB | Sampling time |
| CB | Rate capacity of a BESS |
| Smin | Lower limits of a BESS |
| Smax | Upper limit of a BESS |
| Pmax_ch | Maximum of charging power of a BESS |
| Pmax_f | Maximum of discharging power of a BESS |
| Pc | Maximum available charging power of a BESS |
| Pd | Maximum available discharging power of a BESS |
| at | White noise time series |
| zt | Time series |
| ϕ, θ | Constants in ARMA |
| F | Backward difference operator |
| Td | Dispathcing interval |
| PD/yref | Dispatching power |
| α | Balance coefficient of the tracking performance and control action |
| mp/p | Prediction horizon |
| mc | Control horizon |
| y | Predicted system response |
| A/B1/B2/C | Model parameter for expression (2) |
| Y | Predicted output in matrix form |
| U | Control value in matrix form |
| D | Disturbance in matrix form |
| G/K/L/Ψ/W | The matrices after being processed |
| Q/R | Weight matrices |
| H/f | Matrices in standardquadratic programming |
| Aineq | Liner inequality matrix |
| bineq | Liner inequality vetor |
| β | Interation variable |
| σ | Diminish interation variable |
| s | Slack variable |
| z | Lagrange multipliers corresponding to s |
| m | The number of inequality constraints |
| r1 | Dual residual |
| r2 | Inequality constraint residual |
| a | Iterative coefficient |
References
- The World Sets New Wind Installations Record: 63,7 GW New Capacity In 2015. Available online: http://www.wwindea.org/the-world-sets-new-wind-installations-record-637-gw-new-capacity-in-2015/ (accessed on 9 August 2016).
- Fox, B. Introduction. In Wind Power Integration: Connection and System Operational Aspects; IET Power and Energy Series: Stevenage, UK, 2007; Volume 50, pp. 77–85. [Google Scholar]
- Bouffard, F.; Galiana, F.D. Stochastic security for operation planning with significant wind power generation. IEEE Trans. Power Syst. 2007, 23, 306–316. [Google Scholar] [CrossRef]
- Liu, J.Z. Basic issues of utilization of large-scale renewable power with high security and efficiency. Proc. CSEE 2013, 33, 1–9. [Google Scholar]
- Barton, J.P.; Infield, D.G. Energy storage and its use with intermittent renewable energy. IEEE Trans. Energy Convers. 2004, 19, 441–448. [Google Scholar] [CrossRef]
- Divya, K.C.; Østergaard, J. Battery energy storage technologies for power system—An overview. Electr. Power Syst. Res. 2008, 79, 511–520. [Google Scholar] [CrossRef]
- Ru, Y.; Kleissl, J.; Martinez, S. Storage size determination for grid-connected photovoltaic systems. IEEE Trans. Sustain. Energy 2013, 4, 68–81. [Google Scholar] [CrossRef]
- Bindner, H.; Lundsager, P. Integration of wind power in the power system. In Proceedings of the 28th Annual Conference of the Industrial Electronics Society, Sevilla, Spain, 5–8 November 2002.
- Teleke, S.; Baran, M.E.; Bhattacharya, S. Optimal Control of Battery Energy Storage for Wind Farm Dispatching. IEEE Trans. Energy Convers. 2010, 25, 787–794. [Google Scholar] [CrossRef]
- Jia, H.X.; Zhang, Y.; Wang, Y.F. Application of Energy storage technology in wind power systems. Renew. Energy 2009, 27, 10–15. [Google Scholar]
- Nguyen, T.T.; Yoo, H.J.; Kim, H.M. A Flywheel Energy Storage System Based on a Doubly Fed Induction Machine and Battery for Microgrid Control. Energies 2015, 8, 5074–5089. [Google Scholar] [CrossRef]
- Teleke, S.; Baran, M.E.; Huang, A. Control strategies for battery storage for wind farm dispatching. IEEE Trans. Energy Convers. 2009, 24, 725–732. [Google Scholar] [CrossRef]
- Wang, X.Y.; Vilathgamuwa, D.M.; Choi, S.S. Determination of battery storage capacity in energy buffer for wind farm. IEEE Trans. Energy Convers. 2008, 23, 868–878. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, H. Two-time-scale coordination control for a battery energy storage system to mitigate wind power fluctuations. IEEE Trans. Energy Convers. 2013, 28, 52–61. [Google Scholar] [CrossRef]
- Nguyen, C.L.; Lee, H.H.; Chun, T.W. Cost-optimized battery capacity and short-term power dispatch control for wind farm. IEEE Trans. Ind. Appl. 2015, 51, 595–606. [Google Scholar] [CrossRef]
- Arulampalam, A.; Barnes, M.; Jenkins, N. Power quality and stability improvement of a wind farm using STATCOM supported with hybrid battery energy storage. IEE Proc.-Gener. Transm. Distrib. 2006, 153, 701–710. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, B.; Mao, C. Use of battery energy storage system to improve the power quality and stability of wind farms. In Proceedings of the 26th International Conference on Power system Technology, Chongqing, China, 22–26 October 2006.
- Trung, T.T.; Ahn, S.J.; Choi, J.H. Real-Time Wavelet-Based Coordinated Control of Hybrid Energy Storage Systems for Denoising and Flattening Wind Power Output. Energies 2014, 7, 6620–6644. [Google Scholar] [CrossRef]
- Yoshimoto, K.; Nanahara, T.; Koshimizu, G. New control method for regulating state-of-charge of a battery in hybrid wind power/battery energy storage system. In Proceedings of the Power System Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006.
- Hong, H.S.; Jiang, Q.Y.; Yan, Y.T. An optimization control method of battery smoothed in real time. Autom. Electr. Power Syst. 2012, 37, 103–109. [Google Scholar]
- Vahidi, A.; Stefanopoulou, A.; Peng, H. Current management in a hybrid fuel cell power system: A model-predictive control approach. IEEE Trans. Control Syst. Technol. 2006, 14, 1047–1057. [Google Scholar] [CrossRef]
- Kassem, A.M.; Yousef, A.M. Voltage and frequency control of an autonomous hybrid generation system based on linear model predictive control. Sustain. Energy Technol. Assess. 2013, 4, 52–61. [Google Scholar]
- Torreglosa, J.P.; García, P.; Fernández, L.M.; Jurado, F. Energy dispatching based on predictive controller of an off-grid wind turbine/photovoltaic/hydrogen/battery hybrid system. Renew. Energy 2015, 74, 326–336. [Google Scholar] [CrossRef]
- Wu, W.; Xu, J.P.; Hwang, J.J. Multi-loop nonlinear predictive control scheme for a simplistic hybrid energy system. Int. J. Hydrog. Energy, 2009, 34, 3953–3964. [Google Scholar] [CrossRef]
- Kou, P.; Gao, F.; Guan, X.H. Stochastic predictive control of battery energy storage for wind farm dispatching: Using probabilistic wind power forecasts. Renew. Energy 2015, 80, 286–300. [Google Scholar] [CrossRef]
- Roy, B.; Bipul, K.; Rajesh, K. Unit Commitment Risk Analysis of Wind Integrated Power Systems. IEEE Trans. Power Syst. 2009, 24, 930–939. [Google Scholar]
- Sodium Sulfur Battery Catalog; NGK Insulators Ltd.: Tokyo, Japan, 2009.












| Method | Max Deviation | Min Deviation (MW) | Mean (MW) | Std. (MW) | |
|---|---|---|---|---|---|
| Value (MW) | Time | ||||
| IN-MPC | 1.478 | 10 | 0 | 0.2047 | 0.1096 |
| QP-MPC | 1.537 | 13 | 0 | 0.4139 | 0.1706 |
| Method | Max Deviation | Min Deviation (MW) | Mean (MW) | Std. (MW) | |
|---|---|---|---|---|---|
| Value (MW) | Time | ||||
| IN-MPC | 0.524 | 21 | 0 | 0.0689 | 0.0142 |
| QP-MPC | 0.537 | 19 | 0 | 0.1529 | 0.0385 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Wen, J.; Chan, K.-w.; Cai, G. Dispatching of Wind/Battery Energy Storage Hybrid Systems Using Inner Point Method-Based Model Predictive Control. Energies 2016, 9, 629. https://doi.org/10.3390/en9080629
Yang D, Wen J, Chan K-w, Cai G. Dispatching of Wind/Battery Energy Storage Hybrid Systems Using Inner Point Method-Based Model Predictive Control. Energies. 2016; 9(8):629. https://doi.org/10.3390/en9080629
Chicago/Turabian StyleYang, Deyou, Jiaxin Wen, Ka-wing Chan, and Guowei Cai. 2016. "Dispatching of Wind/Battery Energy Storage Hybrid Systems Using Inner Point Method-Based Model Predictive Control" Energies 9, no. 8: 629. https://doi.org/10.3390/en9080629
APA StyleYang, D., Wen, J., Chan, K. -w., & Cai, G. (2016). Dispatching of Wind/Battery Energy Storage Hybrid Systems Using Inner Point Method-Based Model Predictive Control. Energies, 9(8), 629. https://doi.org/10.3390/en9080629