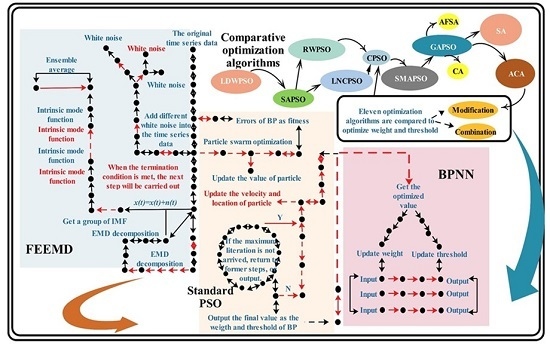
Comparative Study of Hybrid Models Based on a Series of Optimization Algorithms and Their Application in Energy System Forecasting
Abstract
:1. Introduction
1.1. Statistical Forecasting Methods
1.2. Physical Forecasting Methods
1.3. Intelligent Forecasting Methods
1.4. Hybrid Forecasting Methods
1.5. Contribution
- (1)
- Focus on a complex system. From the review above, we know that most researchers focus primarily on the forecasting of a single indicator, whereas this paper explores a new idea and constructs seven hybrid models based on PSO to forecast short-term wind speed, electrical load and electricity price in the electrical power system. The effectiveness of the hybrid models is validated by proving their performance experimentally. The proposed models address the forecasting problems in the complex system, which is of great significance with high practicability.
- (2)
- Address the non-stationary data. One of the main features of the proposed hybrid models is the integration of already existing models and algorithms, which jointly show advances over the current state of the art [44]. The selection of the type of neural network for the best performance depends on the data sources [45]; therefore, we need to compare the proposed models with other well-known techniques by using the same data sets to prove their performance effectively and efficiently. The hybrid models can handle non-stationary data well [46].
- (3)
- High forecasting accuracy. Hybrid models can also help escape a local optimum and search for the global optimum through optimizing the threshold and weight values. In addition, the proposed hybrid models can achieve high forecasting accuracy in multiple-step forecasting, as proven in Experiment IV. This paper develops many types of PSOs: different types of inner modifications of PSO are compared, and combinations of PSO with other artificial intelligence optimization algorithms are analysed. In distinct situations, different types of PSO should be applied.
- (4)
- Fast computing speed. The hybrid models have a fast computing speed, allowing short-term forecasting of the electrical power system with high efficiency.
- (5)
- Scientific evaluation metrics. The forecasting validity degree (FVD) is introduced to evaluate the performance of the model, in addition to the common evaluation metrics, such as the mean absolute percentage error (MAPE), mean absolute error (MAE) and mean square error (MSE). Thus, we can achieve a more comprehensive evaluation of the developed hybrid models.
2. Time Series Decomposition
3. Optimization of Back Propagation Neural Network
3.1. Standard PSO Algorithm
3.2. Modified PSO Algorithm
3.2.1. Linear Decreasing Inertia Weight Particle Swarm Optimization (LDWPSO)
3.2.2. Self-Adaptive Inertia Weight Particle Swarm Optimization (SAPSO)
3.2.3. Random Weight Particle Swarm Optimization (RWPSO)
3.2.4. Constriction Factor Particle Swarm Optimization (CPSO)
3.2.5. Learning Factor Change Particle Swarm Optimization (LNCPSO)
3.3. Combination with Other Intelligent Algorithms
3.3.1. Combination with Simulated Annealing Algorithm (SMAPSO)
- (a)
- Set the initial temperature , and generate the initial solution .
- (b)
- Repeat the following steps at temperature until arrives at a balanced state.
- (c)
- Annealing. ; if the condition of convergence is met, then the annealing process ends. Otherwise, return to (b).
3.3.2. Combination with Genetic Algorithm (GAPSO)
3.4. Back Propagation Neural Network
3.5. The Hybrid Models
- (a)
- One-step forecasting: The forecasted value is obtained based on the historical time series , and t is the sampled time of the time series.
- (b)
- Two-step forecasting: The forecasted value is obtained based on the historical time series and the previously forecasted value .
- (c)
- Three-step forecasting: The forecasted value is calculated based on the historical time series and the previously forecasted values .
4. Experimental Simulation and Results Analysis
4.1. Data Sets
4.2. Evaluation Metrics
4.2.1. Evaluation of Multiple Points
4.2.2. Forecasting Validity Degree
4.2.3. Diebold Mariano Test
4.3. Experimental Setup
4.4. Experiment I
- (a)
- First of all, for the comparison of FE-NPSO-BP, in one-step forecasting, LNCPSO has the best MAPE, MAE and FVD at 2.08%, 85.468 and 0.926, respectively. GAPSO achieves better MSE in one-step forecasting. For three-step forecasting, RWPSO has the lowest MAPE, at 2.72%. The forecasting error between the combined PSO and modified PSO is small. Therefore, in summary, the forecasting result is similar for modified PSO and combined PSO when forecasting electoral load time series.
- (b)
- For BP optimized by different algorithms, in one-step forecasting, FE-CA-BP has the lowest MAPE, which is 2.18%. FE-PSO-BP and FE-ACA-BP have the best MAPE with 2.69% and 2.90%. For the other indexes, different models achieve different values. Therefore, it can be summarized that BP optimized by other single optimization algorithms is less stable, and it is difficult to find a suitable method to forecast the electrical load time series accurately.
- (c)
- Finally, compared to conventional models, GM has the best forecasting performance, and the MAPE is 2.96% and 2.25% in three-step and one-step forecasting, respectively. The MAPE of ARIMA in two-step forecasting is 2.77%. In general, the performance of machine-learning-based methods is better than for traditional statistical models.
4.5. Experiment II
- (a)
- For the short-term wind speed time series and all forecasting steps, the combined PSO algorithms achieve better forecasting accuracy. GAPSO has the best forecasting results, with a MAPE of 3.18% and an FVD of 0.905 in one-step forecasting. In comparison, PSO-BP has the worst performance, and the MAPE increases by 0.57% compared with GAPSO because FEEMD denoises the original time series and makes the processed data smoother. It can be concluded that the combined algorithms are more effective in forecasting the short-term wind speed, which is because GA has a stronger ability to search for the global optimum and achieve a faster rate of convergence.
- (b)
- Among the separate types of optimization algorithms, FE-CA-BP and FE-AFSA-BP have the best forecasting performance. In comparison, the proposed hybrid model, FE-GAPSO-BP, increases the forecasting accuracy by 0.06%, 0.18% and 0.17%. The forecasting differences among different types of optimization algorithms are not significant.
- (c)
- When comparing the proposed hybrid models with traditional forecasting methods, BP, ENN and GM achieve the best MAPE, with 3.31%, 4.55% and 5.31%. Although ARIMA has better MAEs in one- and two-step forecasting, the other indexes such as MSE and FVD are worse. BP has a better FVD, but its forecasting performance is worse than that of GAPSO because the output of the single BP is not stable and has a relatively low capability for fault tolerance.
4.6. Experiment III
- (a)
- For the electricity price time series, SMAPSO has the lowest MAPE and the highest FVD. The MAPE values for GAPSO are similar to the values for SMAPSO, which means that the combined PSO algorithm is more effective in forecasting the electricity price. In one-step forecasting, SMAPSO increases the forecasting accuracy by 0.66%.
- (b)
- When comparing different types of algorithms, the MAPE value of FE-SA-BP is the best, with 5.29% for one-step forecasting, the MAPE of FE-AFSA-BP achieves the best value of 5.68% for two-step forecasting, and FE-PSO-BP has the best MAPE at 6.17%. BP optimized by NPSOs outperforms the other algorithms, including AFSA, CA, GA, PSO, ACA and SA. Therefore, the combination of algorithms can adopt the advantages of the single ones. Both the ability to search for the global optimum and the convergence rate are enhanced.
- (c)
- Finally, consistent with the results of the electrical load and wind speed time series data, the machine-learning-based algorithms have better forecasting performance than the conventional algorithms, such as ARIMA, FAC and SAC, because the indexes of MAE, MSE and FVD are all better as well.
5. Discussion
5.1. Statistical Model
5.2. Artificial Intelligence Neural Network
5.3. Significance of Forecasting Results
5.4. Discussion of the Effectiveness of Fast Ensemble Empirical Mode Decomposition
5.5. Comparison of Different Types of Particle Swarm Optimization Algorithms
5.6. Selection of the Hidden and Input Layers for Back Propagation
5.7. Steps of Forecasting
5.8. Running Time
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ARMA | Auto regressive moving model |
| ENN | Elman neural network |
| ARIMA | Autoregressive integrated moving average model |
| VAR | Vector auto-regressive model |
| RMSE | Root mean square error |
| ANN | Artificial neural networks |
| GARCH | Generalized autoregressive conditional heteroskedasticity |
| MAPE | Mean absolute percentage error |
| CMI | Conditional mutual information |
| MAE | Mean absolute error |
| MSE | Mean square error |
| EEMD | Ensemble empirical model decomposition |
| AFS | Axiomatic fuzzy set |
| FVD | Forecasting validity degree |
| DWT | Discrete wavelet transform |
| FEEMD | Fast ensemble empirical model decomposition |
| NWP | Numerical weather prediction |
| ABC | Artificial bee colony |
| AFS | Axiomatic fuzzy set |
| MEA | Mind evolutionary algorithm |
| STMP | Swarm-based translation-invariant morphological precision |
| MLP | Multi layer perceptron |
| ASA | Ant swarm algorithm |
| CA | Cuckoo algorithm |
| MMNN | Modular morphological neural network |
Appendix A
| Pseudo code of EEMD algorithm |
| Input: |
| —a sequence of sample data |
| Output: |
| —a sequence of forecasting data |
| Parameters: |
| M—the number of ensemble for EEMD algorithm. |
| k—the amplitude of the added white noise in EEMD algorithm. |
| Nstd—ratio of the standard deviation of the added noise and that of |
| itermax—the iterations of the total loop of EEMD algorithm. |
| TNM—the number of intrinsic mode function components. |
| 1: /* Read data, find out standard deviation, divide all data by standard deviation */ |
| 2: Evaluate as total IMF number and assign 0 to TNM2; |
| 3: FOR EACH kk=1:1:TNM2 DO |
| 4: Allmode (ii, kk)=0.0 where ii=1:1:xsize; |
| 5: END FOR |
| 6: Do EEMD, EEMD loop start; |
| 7: /* Add white noise to the original data */ |
| 8: FOR EACH i=1: xsize DO |
| 9: Temp=randn (1,1) * Nstd; |
| 10: END FOR |
| 11: /* Assign original data to the first column */ |
| 12: WHILE nmode <= TNM DO |
| 13: Xstart=xtend; /*last loop value assign to new iteration loop */ |
| 14: END WHILE |
| 15: /* Sift 10 times to get IMF__Sift loop start */ |
| 16: WHILE iter <= 10 DO |
| 17: upper = spline (spmax (:, 1), spmax (:, 2), dd); */ upper spline bound of this sift */ |
| 18: lower = spline (spmin (:, 1), spmin (:, 2), dd); */ lower spline bound of this sift */ |
| 19: Iter = Iter + 1; |
| 20: END WHILE |
| 21: /* After getting all IMFs, the residual is over and put them in the last column */ |
| 22: Decompose according to EMD and Calculate the mean: ; |
| 23: Return |
Appendix B
| Pseudo-code of standard PSO algorithm |
| Input: |
| —a sequence of sample data |
| —a sequence of testing data |
| Output: |
| ___this value can satisfy the best fitness after the global particle searching. |
| Parameters: |
| q__the number of sample data used to construct the network of BPNN model. |
| d__the number of data to be used to perform the forecasting in fitness function. |
| Pop size__the number of populations for the particle swarm. |
| ,__the cognitive and social weight of PSO algorithm. Typically, . |
| Itermax__the maximum number of iterations. |
| 1: /* Initialize pop size with the values between 0 and 1 */ |
| 2: FOR EACH DO |
| 3: ; |
| 4: END FOR |
| 5: /* Initialize the velocity and position of each particle in the population */ |
| 6: /* Initialize the velocity of the particle */ |
| 7: /* Initialize the position of the particle */ |
| 8: /* Find the best value of repeatedly until the maximum iterations are reached */ |
| 9: WHILE DO |
| 10: /* Find the best fitness value for each particle in the population */ |
| 11: FOR EACH DO |
| 12: Build BPNN by applying with the value; |
| 13: Calculate by BPNN; |
| 14: /* Choose the best fitness value of the ith particle in history */ |
| 15: IF gBest > pBesti THEN |
| 16: gBest = pBesti; |
| 17: ; |
| 18: END IF |
| 19: END FOR |
| 20: /* Update the values of all the particles by using PSO’s evolution equations */ |
| 21: FOR EACH DO |
| 22: |
| 23: |
| 24: END FOR |
| 25: iter = iter + 1; /* Until iter arrives at the value of itermax */ |
| 26: END WHILE |
| 27: Return : the best fitness after the global particle searching |
References
- Wang, J.Z.; Hu, J.M.; Ma, K.L.; Zhang, Y.X. A self-adaptive hybrid approach for wind speed forecasting. Renew. Energy 2015, 78, 374–385. [Google Scholar] [CrossRef]
- Ladislav, Z. Wind speed forecast correction models using polynomial neural networks. Renew. Energy 2015, 83, 998–1006. [Google Scholar]
- Lu, X.; Wang, J.Z.; Cai, Y.; Zhao, J. Distributed HS-ARTMAP and its forecasting model for electricity load. Appl. Soft Comput. 2015, 32, 13–22. [Google Scholar] [CrossRef]
- Koprinska, I.; Rana, M.; Agelidis, V.G. Correlation and instance based feature selection for electricity load forecasting. Knowl.-Based Syst. 2015, 82, 29–40. [Google Scholar] [CrossRef]
- Kaytez, F.; Taplamacioglu, M.C.; Cam, E.; Hardalac, F. Forecasting electricity consumption: A comparison of regression analysis, neural networks and least squares support vector machines. Int. J. Electr. Power 2015, 67, 431–438. [Google Scholar] [CrossRef]
- Raviv, E.; Bouwman, K.E.; Dijk, D.V. Forecasting day-ahead electricity prices: Utilizing hourly prices. Energy Econ. 2015, 50, 227–239. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sust. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Seetharaman, K. Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energy 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Wang, J.Z.; Zhao, G.; Dong, Y. Application of residual modification approach in seasonal ARIMA for electricity demand forecasting: A case study of China. Energy Policy 2012, 48, 284–294. [Google Scholar] [CrossRef]
- Shukur, O.B.; Lee, M.H. Daily wind speed forecasting through hybrid KF-ANN model based on ARIMA. Renew. Energy 2015, 76, 637–647. [Google Scholar] [CrossRef]
- Babu, C.N.; Reddy, B.E. A moving-average filter based hybrid ARIMA-ANN model for forecasting time series data. Appl. Soft Comput. 2014, 23, 27–38. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivera, W. Wind speed forecasting in three different regions of Mexico, using a hybrid ARIMA-ANN model. Renew. Energy 2010, 35, 2732–2738. [Google Scholar] [CrossRef]
- Yahyai, S.A.; Charabi, Y.; Gastli, A. Review of the use of numerical weather prediction (NWP) models for wind energy assessment. Renew. Sust. Energy Rev. 2010, 14, 3192–3198. [Google Scholar] [CrossRef]
- Zhang, J.; Draxl, C.; Hopson, T.; Monache, L.D.; Vanvyve, E.; Hodge, B.M. Comparison of numerical weather prediction based deterministic and probabilistic wind resource assessment methods. Appl. Energy 2015, 156, 528–541. [Google Scholar] [CrossRef]
- Giorgi, M.G.; Ficarella, A.; Tarantino, M. Assessment of the benefits of numerical weather predictions in wind power forecasting based on statistical methods. Energy 2011, 36, 3968–3978. [Google Scholar] [CrossRef]
- Felice, M.D.; Alessandri, A.; Ruti, P.M. Electricity demand forecasting over Italy: Potential benefits using numerical weather prediction models. Electr. Power Syst. Res. 2013, 104, 71–79. [Google Scholar] [CrossRef]
- Sile, T.; Bekere, L.; Frisfelde, D.C.; Sennikovs, J.; Bethers, U. Verification of numerical weather prediction model results for energy applications in Latvia. Energy Procedia 2014, 59, 213–220. [Google Scholar] [CrossRef]
- Patterson, D.W. Artificial Neural Networks: Theory and Applications; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. New wind speed forecasting approaches using fast ensemble empirical model decomposition, genetic algorithm, mind evolutionary algorithm and artificial neural networks. Renew. Energy 2015, 83, 1066–1075. [Google Scholar] [CrossRef]
- Lou, C.W.; Dong, M.C. A novel random fuzzy neural networks for tackling uncertainties of electric load forecasting. Int. J. Electr. Power 2015, 73, 34–44. [Google Scholar] [CrossRef]
- Coelho, L.; Santos, A. A RBF neural network model with GARCH errors: Application to electricity price forecasting. Electr. Power Syst. Res. 2011, 81, 74–83. [Google Scholar] [CrossRef]
- Keles, D.; Scelle, J.; Paraschiv, F.; Fichtner, W. Extended forecast methods for day-ahead electricity spot prices applying artificial neural networks. Appl. Energy 2016, 162, 218–230. [Google Scholar] [CrossRef]
- Anbazhagan, S.; Kumarappan, N. A neural network approach to day-ahead deregulated electricity market prices classification. Electr. Power Syst. Res. 2012, 86, 140–150. [Google Scholar] [CrossRef]
- Wang, W.N.; Liu, X.D. Fuzzy forecasting based on automatic clustering and axiomatic fuzzy set classification. Inform. Sci. 2015, 294, 78–94. [Google Scholar] [CrossRef]
- Zhao, F.Q.; Liu, Y.; Zhang, C.; Wang, J.B. A self-adaptive harmony PSO search algorithm and its performance analysis. Expert Syst. Appl. 2015, 42, 7436–7455. [Google Scholar] [CrossRef]
- Chung, S.H.; Chan, H.K.; Chan, F.T.S. A modified genetic algorithm for maximizing handling reliability and recyclability of distribution centers. Expert Syst. Appl. 2013, 40, 7588–7595. [Google Scholar] [CrossRef]
- Arce, T.; Román, P.E.; Velásquez, J.; Parada, V. Identifying web sessions with simulated annealing. Expert Syst. Appl. 2014, 41, 1593–1600. [Google Scholar] [CrossRef]
- Leung, S.Y.S.; Tang, Y.; Wong, W.K. A hybrid particle swarm optimization and its application in neural networks. Expert Syst. Appl. 2012, 39, 395–405. [Google Scholar] [CrossRef]
- Xiao, J.; Ao, X.T.; Tang, Y. Solving software project scheduling problems with ant colony optimization. Comput. Oper. Res. 2013, 40, 33–46. [Google Scholar] [CrossRef]
- Melo, H.; Watada, J. Gaussian-PSO with fuzzy reasoning based on structural learning for training a neural network. Neurocomputing 2016, 172, 405–412. [Google Scholar] [CrossRef]
- Kanna, B.; Singh, S.N. Towards reactive power dispatch within a wind farm using hybrid PSO. Int. J. Electr. Power 2015, 69, 232–240. [Google Scholar] [CrossRef]
- Aghaei, J.; Muttaqi, K.M.; Azizivahed, A.; Gitizadeh, M. Distribution expansion planning considering reliability and security of energy using modified PSO (Particle Swarm Optimization) algorithm. Energy 2014, 65, 398–411. [Google Scholar] [CrossRef]
- Carneiro, T.C.; Melo, S.P.; Carvalho, P.C.; Braga, A.P. Particle swarm optimization method for estimation of Weibull parameters: A case study for the Brazilian northeast region. Renew. Energy 2016, 86, 751–759. [Google Scholar] [CrossRef]
- Bahrami, S.; Hooshmand, R.A.; Parastegari, M. Short-term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization algorithm). Energy 2014, 72, 434–442. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Chen, C.; Li, Y.F. An experimental investigation of two wavelet-MLP hybrid frameworks for wind speed prediction using GA and PSO optimization. Int. J. Electr. Power 2013, 52, 161–173. [Google Scholar] [CrossRef]
- Juang, C.F. A hybrid of genetic algorithm and particle swarm optimization for recurrent network design. IEEE Trans. Syst. Man Cybern B 2004, 34, 997–1006. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Pan, D.F.; Li, Y.F. Forecasting models for wind speed using wavelet, wavelet packet, time series and artificial neural networks. Appl. Energy 2013, 107, 191–208. [Google Scholar] [CrossRef]
- Ghasemi, A.; Shayeghi, H.; Moradzadeh, M.; Nooshyar, M. A novel hybrid algorithm for electricity price and load forecasting in smart grids with demand-side management. Appl. Energy 2016, 177, 40–59. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussion, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sust. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Hu, J.M.; Wang, J.Z.; Zeng, G.W. A hybrid forecasting approach applied to wind speed series. Renew. Energy 2013, 60, 185–194. [Google Scholar] [CrossRef]
- Shi, J.; Guo, J.M.; Zheng, S.T. Evaluation of hybrid forecasting approaches for wind speed and power generation time series. Renew. Sust. Energy Rev. 2012, 16, 3471–3480. [Google Scholar] [CrossRef]
- Velazquez, S.; Carta, J.A.; Matias, J.M. Influence of the input layer signals of ANNs on wind power estimation for a target site: A case study. Renew. Sust. Energy Rev. 2011, 15, 1556–1566. [Google Scholar] [CrossRef]
- Osorio, G.J.; Matias, J.C.; Catalao, J.P. Short-term wind power forecasting using adaptive neuro-fuzzy inference system combined with evolutionary particle swarm optimization, wavelet transform and mutual information. Renew. Energy 2015, 75, 301–307. [Google Scholar] [CrossRef]
- Li, G.; Shi, J. On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 2010, 87, 2313–2320. [Google Scholar] [CrossRef]
- Wang, S.X.; Zhang, N.; Wu, L.; Wang, Y.M. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Li, S.F.; Zhou, W.D.; Yuan, Q.; Geng, S.J.; Cai, D.M. Feature extraction and recognition of ictal EEG using EMD and SVM. Comput. Biol. Med. 2013, 43, 807–816. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Z.; Song, Y.L.; Liu, F.; Hou, R. Analysis and application of forecasting models in wind power integration: A review of multi-step-ahead wind speed forecasting models. Renew. Sust. Energy Rev 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Zhou, Q.P.; Jiang, H.Y.; Wang, J.Z.; Zhou, J.L. A hybrid model for PM2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural network. Sci. Total Environ. 2014, 496, 264–274. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Yeh, C.H.; Young, H.W.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Physica A 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Nieto, P.J.; Fernandez, J.R.; Suarez, V.M.; Muniz, C.D.; Gonzalo, E.G.; Bayon, R.M. A hybrid PSO optimized SVM-based method for predicting of the cyanotoxin content from experimental cyanobacteria concentrations in the Trasona reservoir: A case study in Northern Spain. Appl. Math. Comput. 2015, 260, 170–187. [Google Scholar] [CrossRef]
- Khanna, V.; Das, B.K.; Bisht, D.; Singh, P.K. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- Wang, J.Z.; Jiang, H.; Wu, Y.J.; Dong, Y. Forecasting solar radiation using an optimized hybrid model by cuckoo search algorithm. Energy 2015, 81, 627–644. [Google Scholar] [CrossRef]
- Ren, C.; An, N.; Wang, J.Z.; Li, L.; Hu, B.; Shang, D. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting. Knowl.-Based Syst. 2014, 56, 226–239. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Q.R.; Wang, J.Z.; Liu, M. A rolling grey model optimized by particle swarm optimization in economic prediction. Comput. Intel. 2014, 32, 391–419. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera, V.E.; Chiclana, F. Multiperson decision-making based on multiplicative preference relations. Eur. J. Oper. Res. 2001, 129, 372–385. [Google Scholar] [CrossRef]
- Zhao, W.G.; Wang, J.Z.; Lu, H.Y. Combining forecasts of electricity consumption in China with time-varying weights updated by a high-order Markov chain model. Omega 2014, 45, 80–91. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–265. [Google Scholar]
- Diebold, F.X. Element of Forecasting, 4th ed.; Thomson South-Western: Cincinnati, OH, USA, 2007; pp. 257–287. [Google Scholar]
- Chen, H.; Wan, Q.L.; Wang, Y.R. Refined Diebold-Mariano test methods for the evaluation of wind power forecasting models. Energies 2014, 7, 4185–4198. [Google Scholar] [CrossRef]
- Gao, Y.M. Short-Term Power Load Forecasting Based on BP Neural Network Optimized by GA-PSO Algorithm. Master’s Thesis, Guizhou Normal University, Guiyang, China, 2014. [Google Scholar]





| Models | Variables | Data Set | Ref. |
|---|---|---|---|
| Statistical Forecasting Methods | |||
| Fraction-ARIMA | Wind speed | Hourly data in North Dakota | [9] |
| Fourier and seasonal-ARIMA residual modification model | Electricity demand | 2006–2010 in northwestern China | [10] |
| Kalman filter and ANN based on ARIMA | Wind speed | 2000–2004 in Mosul, Iraq; 2006–2010 in Johor, Malaysia | [11] |
| ARIMA and ANN | Electricity price | 2013 in New South Wales | [12] |
| ARIMA and ANN | Wind speed | Hourly data in California, Zacatecas and Quintana Roo | [13] |
| Physical Forecasting Methods | |||
| MERRA, AnEn based on MERRA and WIND Toolkit | Wind speed | Nine locations in the United States | [15] |
| NWP and ANN | Wind speed; wind power | Three wind turbines in southern Italy | [16] |
| NWP | Electricity load | 2003–2009 in Italy | [17] |
| NWP | Wind speed; wind power | 2013 in Latvia | [18] |
| Intelligent Forecasting Methods | |||
| MLP based on MEA and GA | Wind speed | Stimulated 700 data | [20] |
| RFNN | Electrical load | Hourly data in Macau | [21] |
| RBF | Electricity price | 2008 in Spain | [22] |
| ANN | Electricity price | January to June in 2013 | [23] |
| FFNN and CFNN | Electricity price | 2002 in Spain and 2020 in New York | [24] |
| Clustering and AFS | Electricity price | 2000 in Spain | [25] |
| Evolutionary Algorithms | |||
| PSO for multiobjective optimization | Electrical demand | “Baran and Wu” distribution test system | [33] |
| PSO for Weibull parameter optimization | Wind speed | 2012–2013 in Brazilian northeast region | [34] |
| PSO to optimize the generation coefficient of grey model | Electric load | 2004 in New York and 2010 in Iran | [35] |
| PSO for MLP | Wind speed | 700 data in Qinghai, China | [36] |
| Hybrid Forecasting Methods | |||
| Wavelet-ANNs | Wind speed | 700 data in Qinghai, China | [38] |
| FWPT, CMI, ABC, SVM and ARIMA | Electricity price and load | 2014 In New York and 2010 in Australia | [39] |
| SVM and ANN | Electrical energy consumption | A review of methods | [40] |
| EEMD-SVM | Wind speed | 2001–2006 in Zhangye, China | [41] |
| ARIMA, ANN and SVM | Wind speed; power generation | 2005–2007 in USA | [42] |
| MAPE(%) | Forecasting Degree |
|---|---|
| <10 | Excellent |
| 10–20 | Good |
| 20–50 | Reasonable |
| >50 | Incorrect |
| Different Improved PSO | FE-LDWPSO-BP | FE-SAPSO-BP | FE-RWPSO-BP | FE-CPSO-BP | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 2.97% | 2.75% | 2.38% | 2.90% | 2.71% | 2.28% | 2.72% | 2.70% | 2.31% | 3.06% | 2.72% | 2.46% |
| MAE (m/s) | 103.226 | 98.317 | 89.218 | 97.412 | 94.226 | 88.625 | 108.917 | 96.885 | 86.475 | 98.101 | 95.309 | 86.519 |
| MSE (104 m/s2) | 3.624 | 2.886 | 1.509 | 2.662 | 1.866 | 1.769 | 2.225 | 1.930 | 1.541 | 2.458 | 2.424 | 1.622 |
| FVD | 0.833 | 0.873 | 0.905 | 0.856 | 0.892 | 0.913 | 0.866 | 0.884 | 0.898 | 0.849 | 0.892 | 0.917 |
| Index | FE-LNCPSO-BP | FE-SMAPSO-BP | FE-GAPSO-BP | PSO-BP | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 2.81% | 2.64% | 2.08% | 2.96% | 2.84% | 2.11% | 2.88% | 2.77% | 2.32% | 3.45% | 3.39% | 3.12% |
| MAE (m/s) | 96.698 | 92.473 | 85.468 | 101.383 | 93.627 | 90.127 | 98.732 | 91.486 | 95.237 | 100.245 | 98.706 | 90.008 |
| MSE (104 m/s2) | 2.176 | 1.583 | 1.338 | 2.979 | 1.761 | 1.683 | 2.878 | 1.464 | 1.335 | 3.625 | 3.258 | 1.967 |
| FVD | 0.896 | 0.915 | 0.926 | 0.837 | 0.862 | 0.882 | 0.882 | 0.914 | 0.924 | 0.810 | 0.861 | 0.873 |
| Optimization algorithms | FE-AFSA-BP | FE-CA-BP | FE-GA-BP | FE-PSO-BP | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 2.96% | 2.76% | 2.22% | 3.02% | 2.73% | 2.18% | 2.94% | 2.82% | 2.39% | 3.01% | 2.69% | 2.61% |
| MAE (m/s) | 112.316 | 101.245 | 92.618 | 118.205 | 98.313 | 90.103 | 106.374 | 92.425 | 87.339 | 101.095 | 93.687 | 90.105 |
| MSE (104 m/s2) | 2.437 | 1.896 | 1.728 | 2.416 | 2.128 | 1.624 | 2.289 | 1.826 | 1.655 | 2.316 | 1.774 | 1.614 |
| FVD | 0.851 | 0.884 | 0.914 | 0.842 | 0.893 | 0.921 | 0.862 | 0.881 | 0.909 | 0.847 | 0.892 | 0.911 |
| Index | FE-ACA-BP | FE-SA-BP | ||||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | |||||||
| MAPE | 2.90% | 2.71% | 2.35% | 2.92% | 2.83% | 2.36% | ||||||
| MAE (m/s) | 103.884 | 97.662 | 91.038 | 104.239 | 97.186 | 88.495 | ||||||
| MSE (104 m/s2) | 2.594 | 1.889 | 1.526 | 2.719 | 1.872 | 1.585 | ||||||
| FVD | 0.849 | 0.872 | 0.904 | 0.856 | 0.895 | 0.918 | ||||||
| Conventional algorithms | ARIMA | FAC | SAC | GM | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 3.27% | 2.77% | 2.41% | 3.20% | 2.82% | 2.58% | 3.12% | 2.87% | 2.33% | 2.96% | 2.79% | 2.34% |
| MAE (m/s) | 100.033 | 92.746 | 83.215 | 112.287 | 108.159 | 92.105 | 109.452 | 95.483 | 95.682 | 98.891 | 96.625 | 87.138 |
| MSE (104 m/s2) | 2.416 | 1.924 | 1.661 | 2.339 | 1.876 | 1.579 | 2.748 | 2.059 | 1.624 | 2.354 | 1.776 | 1.496 |
| FVD | 0.802 | 0.853 | 0.886 | 0.789 | 0.842 | 0.873 | 0.819 | 0.855 | 0.894 | 0.830 | 0.857 | 0.881 |
| Index | BP | ENN | ||||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | |||||||
| MAPE | 2.98% | 2.79% | 2.45% | 3.08% | 2.91% | 2.39% | ||||||
| MAE (m/s) | 111.558 | 102.287 | 95.415 | 96.514 | 90.132 | 88.666 | ||||||
| MSE (104 m/s2) | 2.663 | 1.948 | 1.613 | 2.514 | 1.827 | 1.408 | ||||||
| FVD | 0.822 | 0.858 | 0.874 | 0.810 | 0.847 | 0.889 | ||||||
| Different Improved PSO | FE-LDWPSO-BP | FE-SAPSO-BP | FE-RWPSO-BP | FE-CPSO-BP | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 5.38% | 4.38% | 3.25% | 5.35% | 4.52% | 3.33% | 5.44% | 4.49% | 3.27% | 5.28% | 4.71% | 3.29% |
| MAE (m/s) | 1.354 | 0.899 | 0.528 | 1.469 | 0.904 | 0.621 | 1.183 | 0.945 | 0.613 | 1.448 | 1.106 | 0.753 |
| MSE (104 m/s2) | 0.624 | 0.531 | 0.456 | 0.608 | 0.497 | 0.386 | 0.594 | 0.493 | 0.374 | 0.618 | 0.523 | 0.406 |
| FVD | 0.813 | 0.854 | 0.878 | 0.826 | 0.846 | 0.883 | 0.834 | 0.862 | 0.894 | 0.855 | 0.880 | 0.897 |
| Index | FE-LNCPSO-BP | FE-SMAPSO-BP | FE-GAPSO-BP | PSO-BP | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 5.21% | 4.67% | 3.36% | 4.99% | 4.52% | 3.22% | 5.01% | 4.26% | 3.18% | 5.96% | 4.93% | 3.75% |
| MAE (m/s) | 1.443 | 0.824 | 0.529 | 0.912 | 0.614 | 0.505 | 1.154 | 0.718 | 0.417 | 1.689 | 1.441 | 0.820 |
| MSE (104 m/s2) | 0.593 | 0.478 | 0.396 | 0.608 | 0.453 | 0.325 | 0.578 | 0.429 | 0.331 | 0.662 | 0.593 | 0.512 |
| FVD | 0.842 | 0.866 | 0.890 | 0.861 | 0.882 | 0.901 | 0.852 | 0.873 | 0.905 | 0.808 | 0.823 | 0.849 |
| Optimization algorithms | FE-AFSA-BP | FE-CA-BP | FE-GA-BP | FE-PSO-BP | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 5.18% | 4.89% | 3.25% | 5.63% | 4.44% | 3.24% | 5.37% | 4.76% | 3.41% | 5.22% | 4.65% | 3.64% |
| MAE (m/s) | 1.226 | 0.941 | 0.651 | 1.287 | 0.809 | 0.543 | 1.449 | 0.978 | 0.503 | 1.287 | 0.835 | 0.498 |
| MSE (104 m/s2) | 0.612 | 0.513 | 0.376 | 0.582 | 0.453 | 0.374 | 0.605 | 0.583 | 0.426 | 0.557 | 0.429 | 0.351 |
| FVD | 0.841 | 0.866 | 0.872 | 0.837 | 0.859 | 0.894 | 0.826 | 0.861 | 0.902 | 0.837 | 0.865 | 0.888 |
| Index | FE-ACA-BP | FE-SA-BP | ||||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | |||||||
| MAPE | 5.48% | 4.71% | 3.30% | 5.35% | 4.73% | 3.26% | ||||||
| MAE (m/s) | 1.183 | 0.844 | 0.527 | 1.319 | 1.003 | 0.628 | ||||||
| MSE (104 m/s2) | 0.623 | 0.476 | 0.395 | 0.606 | 0.504 | 0.359 | ||||||
| FVD | 0.831 | 0.863 | 0.898 | 0.822 | 0.854 | 0.897 | ||||||
| Conventional algorithms | ARIMA | FAC | SAC | GM | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 5.66% | 4.59% | 3.49% | 5.59% | 4.72% | 3.57% | 5.48% | 4.63% | 3.50% | 5.31% | 4.70% | 3.37% |
| MAE (m/s) | 1.738 | 0.696 | 0.421 | 1.824 | 1.548 | 1.039 | 1.626 | 1.117 | 0.945 | 1.593 | 1.215 | 0.786 |
| MSE (104 m/s2) | 0.683 | 0.626 | 0.519 | 0.662 | 0.594 | 0.417 | 0.602 | 0.517 | 0.385 | 0.599 | 0.452 | 0.378 |
| FVD | 0.802 | 0.812 | 0.845 | 0.826 | 0.844 | 0.876 | 0.845 | 0.855 | 0.883 | 0.826 | 0.858 | 0.880 |
| Index | BP | ENN | ||||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | |||||||
| MAPE | 5.62% | 4.71% | 3.54% | 5.49% | 4.55% | 3.36% | ||||||
| MAE (m/s) | 1.446 | 1.217 | 0.863 | 1.349 | 0.827 | 0.663 | ||||||
| MSE (104 m/s2) | 0.617 | 0.489 | 0.367 | 0.588 | 0.429 | 0.377 | ||||||
| FVD | 0.841 | 0.868 | 0.885 | 0.829 | 0.847 | 0.881 | ||||||
| Different Improved PSO | FE-LDWPSO-BP | FE-SAPSO-BP | FE-RWPSO-BP | FE-CPSO-BP | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 6.26% | 5.75% | 5.12% | 6.33% | 5.79% | 5.26% | 6.27% | 5.66% | 5.08% | 6.21% | 5.77% | 5.08% |
| MAE (m/s) | 4.217 | 3.624 | 2.995 | 4.033 | 3.719 | 2.464 | 3.965 | 3.421 | 2.467 | 3.421 | 3.056 | 2.429 |
| MSE (104 m/s2) | 47.628 | 39.175 | 20.006 | 25.498 | 23.127 | 16.514 | 39.672 | 24.194 | 19.554 | 32.177 | 22.316 | 20.007 |
| FVD | 0.794 | 0.829 | 0.856 | 0.787 | 0.825 | 0.851 | 0.786 | 0.833 | 0.858 | 0.762 | 0.815 | 0.843 |
| Index | FE-LNCPSO-BP | FE-SMAPSO-BP | FE-GAPSO-BP | PSO-BP | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 6.39% | 5.50% | 5.11% | 6.14% | 5.48% | 4.92% | 6.23% | 5.50% | 4.97% | 7.18% | 6.14% | 5.58% |
| MAE (m/s) | 4.116 | 3.547 | 2.469 | 3.858 | 3.129 | 2.318 | 3.964 | 3.252 | 2.179 | 4.665 | 4.193 | 3.217 |
| MSE (104 m/s2) | 41.759 | 30.625 | 22.479 | 35.175 | 21.428 | 18.176 | 30.987 | 23.165 | 18.550 | 56.423 | 44.229 | 30.706 |
| FVD | 0.782 | 0.831 | 0.855 | 0.801 | 0.845 | 0.873 | 0.775 | 0.824 | 0.856 | 0.742 | 0.808 | 0.812 |
| Optimization algorithms | FE-AFSA-BP | FE-CA-BP | FE-GA-BP | FE-PSO-BP | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 6.31% | 5.68% | 5.33% | 6.46% | 5.92% | 5.48% | 6.44% | 5.71% | 5.23% | 6.17% | 5.81% | 5.40% |
| MAE (m/s) | 4.331 | 3.902 | 2.886 | 4.174 | 3.628 | 2.596 | 4.333 | 3.714 | 2.467 | 4.195 | 3.812 | 2.759 |
| MSE (104 m/s2) | 44.138 | 33.965 | 23.004 | 44.239 | 33.547 | 22.695 | 43.996 | 35.368 | 22.510 | 37.474 | 26.615 | 18.691 |
| FVD | 0.774 | 0.815 | 0.832 | 0.789 | 0.830 | 0.837 | 0.762 | 0.829 | 0.836 | 0.760 | 0.824 | 0.852 |
| Index | FE-ACA-BP | FE-SA-BP | ||||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | |||||||
| MAPE | 6.25% | 5.94% | 5.33% | 6.45% | 5.70% | 5.29% | ||||||
| MAE (m/s) | 4.118 | 3.956 | 2.741 | 4.208 | 3.595 | 2.617 | ||||||
| MSE (104 m/s2) | 31.098 | 28.667 | 21.094 | 42.065 | 36.172 | 23.108 | ||||||
| FVD | 0.790 | 0.816 | 0.842 | 0.741 | 0.825 | 0.847 | ||||||
| Conventional algorithms | ARIMA | FAC | SAC | GM | ||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | Three-step | Two-step | One-step | |
| MAPE | 6.57% | 5.92% | 5.67% | 6.62% | 6.08% | 5.41% | 6.31% | 5.94% | 5.35% | 6.41% | 5.68% | 5.47% |
| MAE (m/s) | 4.083 | 3.172 | 2.338 | 4.125 | 3.519 | 2.443 | 4.098 | 3.252 | 2.419 | 4.396 | 3.772 | 2.983 |
| MSE (104 m/s2) | 49.176 | 44.155 | 36.128 | 46.008 | 24.019 | 18.662 | 49.216 | 39.205 | 23.178 | 42.074 | 35.102 | 20.316 |
| FVD | 0.753 | 0.792 | 0.831 | 0.730 | 0.768 | 0.802 | 0.765 | 0.815 | 0.822 | 0.783 | 0.824 | 0.849 |
| Index | BP | ENN | ||||||||||
| Three-step | Two-step | One-step | Three-step | Two-step | One-step | |||||||
| MAPE | 6.33% | 5.96% | 5.60% | 6.25% | 5.84% | 5.21% | ||||||
| MAE (m/s) | 4.275 | 3.628 | 2.416 | 4.226 | 3.823 | 2.796 | ||||||
| MSE (104 m/s2) | 38.429 | 24.108 | 19.337 | 39.219 | 25.441 | 23.053 | ||||||
| FVD | 0.761 | 0.829 | 0.854 | 0.786 | 0.825 | 0.839 | ||||||
| Model | Electrical Load | Wind Speed | Electricity Price | |||
|---|---|---|---|---|---|---|
| DM | p-Value | DM | p-Value | DM | p-Value | |
| FE-LDWPSO-BP | 3.657 | 0.0134 | 0.8984 | 0.8661 | 2.146 | 0.0142 |
| FE-SAPSO-BP | 0.264 | 0.7581 | 2.154 | 0.0000 | 2.135 | 0.0112 |
| FE-RWPSO-BP | 3.448 | 0.0065 | 1.356 | 0.6849 | 2.031 | 0.0234 |
| FE-CPSO-BP | 3.998 | 0.0000 | 1.559 | 0.6594 | 1.983 | 0.0252 |
| FE-SMAPSO-BP | 0.0842 | 0.9283 | 2.185 | 0.0000 | 2.066 | 0.0168 |
| FE-GAPSO-BP | 3.469 | 0.0082 | 0.128 | 0.9164 | 1.359 | 0.7426 |
| PSO-BP | 4.375 | 0.0000 | 2.965 | 0.0000 | 2.836 | 0.0000 |
| FE-AFSA-BP | 0.255 | 0.7076 | 0.731 | 0.8642 | 2.328 | 0.0000 |
| FE-CA-BP | 0.237 | 0.6438 | 0.545 | 0.8776 | 2.736 | 0.0000 |
| FE-GA-BP | 3.718 | 0.0000 | 2.139 | 0.0000 | 2.174 | 0.0155 |
| FE-PSO-BP | 4.092 | 0.0000 | 2.772 | 0.0000 | 2.669 | 0.0000 |
| FE-ACA-BP | 3.613 | 0.0000 | 2.063 | 0.0000 | 2.396 | 0.0000 |
| FE-SA-BP | 3.658 | 0.0000 | 1.242 | 0.7015 | 2.223 | 0.0000 |
| ARIMA | 3.826 | 0.0000 | 2.356 | 0.0000 | 2.979 | 0.0000 |
| FAC | 3.987 | 0.0000 | 2.246 | 0.0000 | 2.647 | 0.0000 |
| SAC | 3.472 | 0.0000 | 2.385 | 0.0000 | 2.528 | 0.0000 |
| GM | 3.566 | 0.0000 | 2.246 | 0.0000 | 2.699 | 0.0000 |
| BP | 3.885 | 0.0000 | 2.417 | 0.0000 | 2.874 | 0.0000 |
| ENN | 3.779 | 0.0000 | 2.209 | 0.0000 | 2.008 | 0.0197 |
| Hidden Layer | Input Layer | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 3 | 4 | 5 | 6 | ||
| Electrical load time series | |||||||||
| 5 | 2.95% | 2.86% | 2.72% | 2.88% | 11 | 2.98% | 2.82% | 3.07% | 2.94% |
| 6 | 2.88% | 2.83% | 2.75% | 2.71% | 12 | 2.76% | 2.75% | 3.11% | 2.93% |
| 7 | 2.76% | 2.68% | 2.79% | 2.88% | 13 | 2.69% | 2.81% | 3.15% | 3.01% |
| 8 | 2.82% | 2.71% | 2.84% | 2.92% | 14 | 2.74% | 2.92% | 2.94% | 2.85% |
| 9 | 2.67% | 2.81% | 2.72% | 3.06% | 15 | 2.88% | 2.95% | 2.83% | 2.89% |
| 10 | 2.92% | 2.90% | 2.89% | 3.09% | 16 | 2.92% | 2.74% | 2.70% | 2.94% |
| Short-term wind speed time series | |||||||||
| 5 | 5.10% | 4.99% | 4.98% | 5.08% | 11 | 5.12% | 5.14% | 5.21% | 5.24% |
| 6 | 5.12% | 4.93% | 5.35% | 5.00% | 12 | 4.99% | 5.24% | 5.31% | 5.11% |
| 7 | 5.04% | 5.00% | 5.42% | 5.09% | 13 | 5.05% | 5.19% | 5.16% | 4.99% |
| 8 | 5.22% | 5.21% | 5.17% | 5.15% | 14 | 5.17% | 5.03% | 5.08% | 5.32% |
| 9 | 4.98% | 5.15% | 5.03% | 5.23% | 15 | 5.21% | 5.06% | 4.99% | 5.20% |
| 10 | 5.17% | 5.14% | 5.16% | 5.14% | 16 | 5.05% | 5.18% | 5.31% | 5.39% |
| Electricity price time series | |||||||||
| 5 | 5.92% | 5.91% | 5.90% | 5.77% | 11 | 5.79% | 5.81% | 6.11% | 5.85% |
| 6 | 5.71% | 5.84% | 5.87% | 5.88% | 12 | 5.84% | 5.94% | 6.03% | 5.80% |
| 7 | 6.11% | 6.06% | 5.89% | 6.09% | 13 | 5.84% | 5.96% | 5.92% | 5.81% |
| 8 | 6.02% | 6.18% | 5.91% | 5.99% | 14 | 5.86% | 5.85% | 5.84% | 5.96% |
| 9 | 5.85% | 5.84% | 5.92% | 5.90% | 15 | 6.07% | 6.08% | 6.18% | 5.97% |
| 10 | 5.78% | 5.81% | 6.12% | 5.83% | 16 | 5.99% | 6.14% | 6.23% | 5.91% |
| One-Step | Two-Step | Improvement | Three-Step | Improvement | |
|---|---|---|---|---|---|
| Electrical load time series | |||||
| MAPE | 2.08% | 2.64% | 0.56% | 2.81% | 0.73% |
| MAE (m/s) | 85.468 | 92.473 | 7.005 | 96.698 | 11.230 |
| MSE (104 m/s2) | 1.338 | 1.583 | 0.245 | 2.176 | 0.838 |
| FVD | 0.926 | 0.915 | 0.011 | 0.896 | 0.03 |
| Short-term wind speed time series | |||||
| MAPE | 3.18% | 4.26% | 1.08% | 5.01% | 1.83% |
| MAE (m/s) | 0.417 | 0.718 | 0.301 | 1.154 | 0.737 |
| MSE (m/s2) | 0.331 | 0.429 | 0.098 | 0.578 | 0.247 |
| FVD | 0.905 | 0.873 | 0.032 | 0.852 | 0.053 |
| Electricity price time series | |||||
| MAPE | 4.92% | 5.48% | 0.56% | 6.14% | 1.22% |
| MAE (m/s) | 2.318 | 3.129 | 0.811 | 3.858 | 1.540 |
| MSE (m/s2) | 18.176 | 21.428 | 3.252 | 35.175 | 16.999 |
| FVD | 0.873 | 0.845 | 0.028 | 0.801 | 0.072 |
| Model | Time (s) | Model | Time (s) |
|---|---|---|---|
| FE-LDWPSO-BP | 84.28 | FE-SMAPSO-BP | 118.73 |
| FE-SAPSO-BP | 114.52 | FE-AFSA-BP | 138.74 |
| FE-RWPSO-BP | 71.33 | FE-CA-BP | 161.49 |
| FE-CPSO-BP | 93.10 | FE-GA-BP | 92.18 |
| FE-LNCPSO-BP | 85.21 | FE-ACA-BP | 107.22 |
| FE-SA-BP | 112.55 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Liu, D. Comparative Study of Hybrid Models Based on a Series of Optimization Algorithms and Their Application in Energy System Forecasting. Energies 2016, 9, 640. https://doi.org/10.3390/en9080640
Ma X, Liu D. Comparative Study of Hybrid Models Based on a Series of Optimization Algorithms and Their Application in Energy System Forecasting. Energies. 2016; 9(8):640. https://doi.org/10.3390/en9080640
Chicago/Turabian StyleMa, Xuejiao, and Dandan Liu. 2016. "Comparative Study of Hybrid Models Based on a Series of Optimization Algorithms and Their Application in Energy System Forecasting" Energies 9, no. 8: 640. https://doi.org/10.3390/en9080640
APA StyleMa, X., & Liu, D. (2016). Comparative Study of Hybrid Models Based on a Series of Optimization Algorithms and Their Application in Energy System Forecasting. Energies, 9(8), 640. https://doi.org/10.3390/en9080640