A New Switching Impulse Generator Based on Transformer Boosting and Insulated Gate Bipolar Transistor Trigger Control

Abstract

To make the switching impulse (SI) generator more compact, portable and feasible in field tests, a new approach based on transformer boosting was developed. To address problems such as triggering synchronization and electromagnetic interference involved with the traditional spark gap, an insulated gate bipolar transistor (IGBT) module with drive circuit was employed as the impulse trigger. An optimization design for the component parameters of the primary winding side of the transformer was realized by numerical calculation and error correction. Experiment showed that the waveform parameters of SI and oscillating switching impulse (OSI) voltages generated by the new generator were consistent with the numerical calculation and the error correction. The generator was finally built on a removable high voltage transformer with small size. Thus the volume of the generator is significantly reduced. Experiments showed that the waveform parameters of SI and OSI voltages generated by the new generator were basically consistent with the numerical calculation and the error correction.

1. Introduction

On account of the frequent failures of high voltage power equipment [1,2,3], more attention has been increasingly focused on the impulse withstand voltage test in the field [4], which has become a more stringent and effective method of evaluating the insulation status of power equipment [5,6,7,8]. The traditional impulse generator is built on a Marx circuit, which has been widely applied in high voltage testing and insulation assess for many years. However, the Marx generator is labor intensive and time consuming in replacing the output waveform, and its multiple spark airgap switches are sometimes triggered out of synchrony, especially when the preset voltage is not very high. In addition, electromagnetic interference [9] that arises from the spark discharge makes partial discharge detection difficult. In this study, we tried to use an impulse transformer to magnify the input impulse voltage. The entire equivalent circuit model was analytically analyzed to accurately control the generator output by adjusting only the circuit connected to the primary winding side, and on this basis, a parameter optimization method was proposed.

In addition, instead of the spark gap of the Marx generator, an insulated gate bipolar transistor (IGBT) was used as a trigger switch owing to its good performance in turning on and cutting off the current with a rapid response time and low noise at the instant of triggering. In this study, the generating circuit of the switching impulse (SI) voltage was initially designed, and its circuit parameters were solved by analytical calculation. Subsequently, the influence of the circuit component parameters on the waveform parameters was analyzed, and an optimized method to select the component parameters was proposed. Finally, aperiodic SI voltage and oscillating switching impulse (OSI) voltage were successfully generated by a 50 kV transformer. Moreover, some technical considerations were discussed for improving the output voltage, increasing output power capacity, as well as generating lightning impulse voltage.

2. Principle of Transformer Boosting-Based Impulse Generation

To establish a guide for designing the primary winding side circuit and determining the circuit parameters based on transformer induction, this section first proposed a fourth-order equivalent circuit to generate a SI According to the solution, waveform parameters in pace with variations of the circuit parameters were obtained by calculation. Subsequently, an optimization method was proposed to select the circuit parameters by considering the waveform error (S) and impulse magnification ratio (IMR).

2.1. Equivalent Circuit Analysis

The basic idea for generating an impulse is to input a small impulse into the primary side of a transformer and thus to obtain an amplified impulse at the secondary (high-voltage) side. To achieve a more effective on-off trigger control, the traditional spark gap is replaced with an IGBT module.

The circuit diagram of the principle for generating SI is sketched as shown in Figure 1. Here, power electronic switch K initially stays in the off state as a trigger switch, U₀ is the voltage on C₁ after charging, and L is the wave-modulating inductor for generating an OSI voltage (it is not adopted to generate SI). As the trigger switch is turned on, main capacitor C₁ discharges to wave-modulating capacitor C₂, which is connected in parallel with the primary side of the transformer, and a high-amplitude SI voltage is induced at the secondary side.

The single-phase transformer shown in Figure 1 can be represented by an equivalent T-type circuit, as shown in Figure 2a. Considering that the winding resistance of the test transformer is relatively smaller than the reactance and that the leakage resistance is much smaller than the excitation reactance, the transformer can be represented by an equivalent Γ-type circuit (Figure 2b) [10].

The entire equivalent discharge circuit of the SI voltage is shown in Figure 3. Here, L is the total equivalent inductance of the wave-modulating and the leakage inductance, and C₂ is the total equivalent capacitance of the load and the wave-modulating capacitance.

2.2. Numerical Calculation

2.2.1. Oscillating Switching Impulse Voltage

According to the equivalent circuit previously mentioned, the equivalent circuit of the entire system configuration during discharge can be drawn as shown in Figure 4.

The loop equation of the equivalent circuit can be expressed by Equation (1) in a fourth-order form:

$$\begin{array}{l}L{L}_{\mathrm{m}}{C}_1{C}_2\frac{{\mathrm{d}}^4{i}_{\mathrm{m}}}{\mathrm{d}{t}^4}+(C_1{C}_2{R}_2{L}_{\mathrm{m}}+\frac{L{C}_2{L}_{\mathrm{m}}}{R_1})\frac{{\mathrm{d}}^3{i}_{\mathrm{m}}}{\mathrm{d}{t}^3}+(L{C}_1+L_{\mathrm{m}}{C}_1+\\ \frac{L_{\mathrm{m}}{C}_2{R}_2}{R_1}+L_{\mathrm{m}}{C}_2)\frac{{\mathrm{d}}^2{i}_{\mathrm{m}}}{\mathrm{d}{t}^2}+(C_1{R}_2+\frac{L}{R_1}+\frac{L_{\mathrm{m}}}{R_1})\frac{\mathrm{d}{i}_{\mathrm{m}}}{\mathrm{d}t}+\frac{R_2+R_1}{R_1}{i}_{\mathrm{m}}=0\end{array}$$

(1)

The initial conditions for Equation (1) are described in Equation (2):

$$\{\begin{array}{l}{i}_{\mathrm{m}}|{}_{t=0}=0\\ \frac{\mathrm{d}{i}_{\mathrm{m}}}{\mathrm{d}t}|{}_{t=0}=0\\ \frac{{\mathrm{d}}^2{i}_{\mathrm{m}}}{\mathrm{d}{t}^2}|{}_{t=0}=0\\ \frac{{\mathrm{d}}^3{i}_{\mathrm{m}}}{\mathrm{d}{t}^3}|{}_{t=0}=\frac{U_0}{L{L}_{\mathrm{m}}{C}_2}\end{array}$$

(2)

Indeed, it is very difficult to obtain the explicit analytical expression for a fourth-order equation [11]. To accurately analyze the relationships between the circuit parameters and waveform parameters, the fourth-order Runge-Kutta method was applied to solve these ordinary differential equations [12,13,14]. For Equation (1), the ordinary differential equations can be solved by introducing an intermediate variable, as expressed in Equation (3):

$$y^{\prime }=\mathit{F}\mathit{y}$$

(3)

here:

$$y^{\prime }={(y_1,y_2,y_3,y_4)}^T,y^{\prime }={(y_1^{\prime },y_2^{\prime },y_3^{\prime },y_4^{\prime })}^T$$

(4)

and the coefficient matrix is expressed in Equations (5) and (6):

$$F=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ -\frac{e}{a}& -\frac{d}{a}& -\frac{c}{a}& -\frac{b}{a}\end{array}\right],y_0={(0,0,0,\frac{U_0}{L{L}_{\mathrm{m}}{C}_2})}^T$$

(5)

$$\{\begin{array}{l}a=L{L}_{\mathrm{m}}{C}_1{C}_2\\ b=C_1{C}_2{R}_2{L}_{\mathrm{m}}+\frac{L{C}_2{L}_{\mathrm{m}}}{R_1}\\ c=L{C}_1+L_{\mathrm{m}}{C}_1+\frac{L_{\mathrm{m}}{R}_1{R}_2}{R_1}+L_{\mathrm{m}}{C}_2\\ d=C_1{R}_2+\frac{L}{R_1}+\frac{L_{\mathrm{m}}}{R_1}\\ e=\frac{R_2+R_1}{R_1}\end{array}\{\begin{array}{l}{y}_1=i_{\mathrm{m}}\\ y_1^{\prime }=\frac{\mathrm{d}{i}_{\mathrm{m}}}{\mathrm{d}t}=y_2\\ y_2^{\prime }=\frac{{\mathrm{d}}^2{i}_{\mathrm{m}}}{\mathrm{d}{t}^2}=y_3\\ y_3^{\prime }=\frac{{\mathrm{d}}^3{i}_{\mathrm{m}}}{\mathrm{d}{t}^3}=y_4\\ y_4^{\prime }=-\frac{b}{a}{y}_4-\frac{c}{a}{y}_3-\frac{d}{a}{y}_2-\frac{e}{a}{y}_1\end{array}$$

(6)

The solution vector y in Equation (3) can be solved by the fourth-order Runge–Kutta equation, and curve u₂ of the OSI waveform can be obtained by Equation (7):

$$u_2=L_{\mathrm{m}}\frac{\mathrm{d}{i}_{\mathrm{m}}}{\mathrm{d}t}=L_{\mathrm{m}}{y}_2$$

(7)

2.2.2. Switching Impulse Voltage

The analysis method for SI is similar to that for the OSI, and the only difference from the consideration of the OSI is that the wave-modulating inductance in the primary side is not needed, i.e., L = 0; hence, the circuit can be described by a group of third-order differential equations.

2.3. Selection and Optimization of the Circuit Parameters

Based on the analytical solution of the circuit parameters, the key parameters of the waveform can be determined with numerical computing, such as peak time T_p, half-peak time T₂, enveloping line, and oscillation frequency f. Assuming that T_p and T₂ of the target impulse voltage are T_p’ and T₂’, respectively, the waveform error S can be calculated by Equation (8):

$$S=\frac{{(T_{\mathrm{p}}-T_{\mathrm{p}}^{\prime })}^2}{{T_{\mathrm{p}}^{\prime }}^2}+\frac{{(T_2-T_2^{\prime })}^2}{{T_2^{\prime }}^2}$$

(8)

Apparently, the smaller S is, the closer is the calculated waveform to the target waveform. Consequently, optimal parameters of the component and their combination within a certain range and a minimum S are expected. In addition, the output efficiency of the generator should be taken into consideration. IMR is thus introduced to generally evaluate the output efficiency of this SI voltage generator, as expressed by Equation (9):

$$IMR=\frac{U_{\mathrm{m}}}{U_1}$$

(9)

Here, U_m is the amplitude of the output voltage, and U₁ is the charging voltage on C₁. In fact, the circuit parameters can hardly meet both the requirements for minimum S and maximum IMR simultaneously. Therefore, the selection of the final circuit parameters is a result of a tradeoff between the two key parameters.

2.3.1. Solving the Circuit Parameters for the Given Target Waveform Parameters

The main program and subprogram flowcharts to calculate the circuit parameters are shown in Figure 5 and Figure 6, respectively. Here, the subprogram is used to calculate the waveform curves and parameters using the given circuit component parameters. Initially, parameters C₁, L_m and R₁ are set to fixed values that can hardly be adjusted in practice, and the specific parameters of the target waveform, such as T_p and T₂, are provided. Then, the expected value ranges for C₂, L and R₂ within a group of parameters such as T_p, T₂, S and IMR can be estimated several times by circular computation using the initial value and step length.

Figure 7 shows an example of the S-IMR distribution which can be used for the parameter optimization. Area I in Figure 7 is composed of parameter combinations with small errors. Area II of the parameter combinations with large IMRs and Area III of the intersection of Areas I and II provides the comprehensive optimal selection area in this distribution. In this area, the circuit parameters are given priority with an optimized combination of larger IMR and small error.

2.3.2. Impulse Waveforms Solution Using the Given Circuit Parameters

To more intuitively describe the influence of the circuit parameters on the impulse waveform, the calculation results are illustrated by discussing the SI and OSI voltages.

• Switching impulse voltage

If the circuit parameters are given as L = 0, C₁ = 10 µF, C₂ = 1 µF, L_m = 0.9 H, R₁ = 1155 Ω, R₂ = 56 Ω and U_c1 = 400 V, the corresponding SI could satisfy the waveform parameters recommended by the IEC 60060-3 standard [4] (i.e., T_p = 250 μs and T₂ = 2500 μs), as shown in Figure 6. By changing a single variable, we can observe the variations in T_p, T₂ and U_m with decreasing L_m and increasing C₁, C₂, R₁ and R₂, as shown in Figure 8. The corresponding parameters are listed in

Table 1. Waveform parameters of SI voltage and their corresponding circuit parameters.

No.	C1 (μF)	C2 (μF)	R1 (Ω)	R2 (Ω)	Lm (H)	Tp (μs)	T2 (μs)	Um (V)	IMR
(1)	10	1	1155	56	0.9	250	2500	351.6	0.879
(2)	10	1	1155	56	0.2	205	1193	341.5	0.854
(3)	50	1	1155	56	0.9	298	4895	384.1	0.960
(4)	10	5	1155	56	0.9	712	3344	246.0	0.615
(5)	10	1	11,550	56	0.9	280	2939	357.1	0.893
(6)	10	1	1155	336	0.9	724	2079	286.7	0.717

.

Figure 8 and Table 1 show that both T_p and T₂ decrease with the decrease in L_m. Meanwhile, T_p, T₂, and IMR increase with the increase in C₁. The increases in T_p, T₂, and IMR are not sensitive to the increase in R₁. T_p and T₂ obviously change along with the changes in R₂ and C₂. Further, a positive correlation exists between T_p and R₂, C₂, whereas T₂ shows a positive correlation with C₂ and a negative correlation with R₂. Therefore, adjusting the element parameters of C₂ and R₂ is preferable in practice. Because L_m is an inherent parameter of the transformer and has a nonlinear characteristic with the magnetizing current, the nonlinear curve of L_m should be introduced in every step of the calculation to obtain a simulation result closer to the real output.

• Oscillating switching impulse voltage

An OSI waveform is generated when the circuit is underdamped (i.e., $R_2<2{[L(C_1+C_2)/C_1{C}_2]}^{-1}$). If the circuit parameters are given as the combination of C₁ = 3 μF, C₂ = 0.22 μF, L_m = 1.3 H, R₁ = 2230 Ω, R₂ = 33 Ω and L = 1.2 mH, the OSI waveform has T_p of 50 μs, T₂ of 1000 μs, U_m of 556.0 V and f of 10 kHz, as shown in Figure 9. As L increases, the waveform oscillation becomes more serious, as shown in Figure 10. Some simulations performed by changing circuit parameters C₁, C₂, R₁ and R₂ are listed in

Table 2. Waveform parameters of OSI voltage and their corresponding circuit parameters.

No.	C1 (μF)	C2 (μF)	R1 (Ω)	R2 (Ω)	L (mH)	Lm (H)	Tp (μs)	T2 (μs)	f (Hz)	Um (V)	IMR
(1)	3	0.22	2.23k	33	1.2	1.3	50	1000	10k	555.0	1.388
(2)	3	0.22	2.23k	33	4.9	1.3	100	855	5.0k	631.4	1.579
(3)	10	0.22	2.23k	33	1.2	1.3	52	1966	9.6k	582.1	1.455
(4)	3	1.12	2.23k	33	1.2	1.3	108	1660	4.6k	353.2	0.883
(5)	3	0.22	2.23k	33	1.2	0.5	50	684	10k	555.0	1.388
(6)	3	0.22	22k	33	1.2	1.3	50	1356	10k	558.0	1.395
(7)	3	0.22	1M	33	1.2	1.3	50	1405	10k	558.2	1.396
(8)	3	0.22	1k	33	1.2	1.3	50	701	10k	553.5	1.384
(9)	3	0.22	2.23k	25	1.2	1.3	50	865	10k	591.3	1.478
(10)	3	0.22	2.23k	120	1.2	1.3	77	1520	-	375.6	0.939
(11)	3	0.22	2.23k	180	1.2	1.3	157	1492	-	359.8	0.900

.

The oscillation frequency of OSI is related to both parameters L, C₁, C₂ and R₂. When R₂ is very small, f is determined by the combination of L, C₁ and C₂, as expressed in Equation (10). T_p is actually half of the oscillation period.

$$f=\frac{1}{2T_{\mathrm{p}}}=\frac{1}{2\mathsf{\pi }}\sqrt{\frac{C_1+C_2}{L{C}_1{C}_2}}$$

(10)

When R₂ increases to a critical damping condition (even to an overdamped condition), the waveform stops oscillating. Therefore, the OSI waveform can be converted to an SI waveform by reducing L or improving R₂. In addition, T₂ increases with the increase in C₁, C₂, R₁ and R₂, and slightly decreases with the increase in L.

Similar to SI, IMR can be improved by increasing C₁ or decreasing C₂. Therefore, changing the values of L, R₂ and C₂ is effective to adjust the waveform parameters of OSI.

3. Loop Design of Switching Impulse Generator Based on Transformer Induction

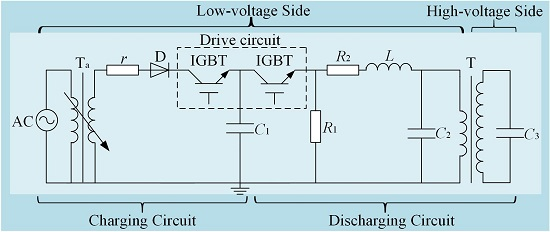
3.1. Insulated Gate Bipolar Transistor Module and Its Drive Circuit

3.1.1. Insulated Gate Bipolar Transistor Module

IGBT acts as a trigger-discharge switch. In the SI voltage generating circuit, the IGBT must withstand the voltage on the primary capacitor before discharge, and the maximum voltage must not exceed the peak voltage of the primary side. Additionally, the switching speed of the IGBT must be sufficiently fast, and its on-off time should be very much lesser than the peak time of the SI voltage. Figure 11 shows that the selected IGBT module in this study is Model FF100R12RT4 (IGBT Module, Infineon, Neubiberg, Germany), which consists of two IGBTs in series and each IGBT has an anti-parallel diode to follow the current and for protection.

3.1.2. Drive Circuit of Insulated Gate Bipolar Transistor

The main function of the IGBT drive circuit is to isolate the control and main circuits. According to the demand, the circuit should not only correctly control the on-off of the IGBT but also provide a certain protection function. In particular, it is supposed to shut off the IGBT when it suffers from overcurrent or overvoltage.

This study designs an IGBT drive circuit, and the schematic diagram is shown in Figure 12. The entire drive circuit consists of a 15 V direct current (DC) power source, channels A and B switches, output channels A and B, a feedback circuit, and a protection circuit. Here, the IGBT drive circuit is powered by the 15 V DC power source. Channels A and B respectively correspond to the left and right IGBTs shown in Figure 11. When the channel switch is closed, the corresponding IGBT tube conducts. According to the design purpose, when the channel A switch is closed and the channel B switch is opened, the left side IGBT tube in Figure 11 conducts, and the power supply begins to charge main capacitor C₁. After the charging is completed, the channel A switch is disconnected. Next, the channel B switch is closed, and the right side IGBT tube conducts. Then, the main capacitor C₁ starts discharging to the primary winding of the transformer. Finally, the secondary side of the transformer induces the desired SI voltage. The output feedback module is mainly used to monitor whether the driver circuit properly works. If abnormal, the driver chip is reset by the protection circuit to protect the driver chip and the IGBT module. Moreover, the driver chip, which mainly completes the control and operation function of the drive circuit, is the core of the entire drive circuit.

3.2. Design of the Main Circuit

3.2.1. Charging Circuit

Because the collector–emitter of the IGBT cannot withstand a negative voltage, it should be connected in series with a diode, which blocks the reverse voltage, or a rectifier. Further, the charging circuits also need a large series resistance r as a current-limiting resistor. However, it extends the charging time of the circuit. The diagram of the charging circuit is shown in Figure 13.

Changing the polarity of the output can be achieved by reversing the connections of diode D and the IGBT. After the IGBT is turned on, main capacitor C₁ can be fully charged within 3–5 time constants (T = rC₁). Before the discharge is triggered, the IGBT should be shut off to ensure that the discharge circuit is isolated from the power supply. The value of the withstand voltage of diode D must be greater than the maximum peak of the output from the power supply, and its through-current capability should exceed the value ωC₁U_m. To determine the value of r, both the maximum current limited by the IGBT parameter and the charging time determined by C₁ should be taken into consideration.

3.2.2. General Circuit

Figure 14 shows the general circuit to generate the SI voltage. The two IGBT module tubes are connected in series and used as switches for the charging and discharging circuits. Secondary voltage of T_a must be matched with the primary voltage of T, i.e., the maximum output of T_a should be greater than the maximum input of T. Considering circuit efficiency, C₁ should be determined by C₃, which is the equivalent capacitance of T or the test sample. Converted into the primary side of T, C₃ and C₂ can be combined into C₂'. Thus, IMR can be estimated by Equation (11):

$$IMR\approx k·\frac{C_1}{C_1+C_2^{\prime }}·\frac{R_1}{R_1+R_2}$$

(11)

4. Experimental Results

Based on the earlier theoretical discussion, each test was implemented according to the following procedures:

i 

Determine the target impulse waveform parameters, such as output voltage, rise time, half peak time and oscillating frequency;

ii 

Define the immutable parameters of the circuit component, such as charging capacitor and transformer;

iii 

Run S-IMR diagram for parameter optimization;

iv 

Adjust the component according to the calculated parameters;

v 

Make a comparison between the actual output and the target impulse waveform.

The voltage waveforms were recorded by a digital oscilloscope (WaveSurfer 64Xs-B, LeCroy, New York, NY, USA) and a high voltage probe (P6015, Tektronix, Beaverton, OR, USA) which is in parallel connection with C₃. Further, the IMR and error sources between the actual and theoretical waveforms are analyzed in this section.

4.1. Experimental Results and Analysis

In the test, a 200 V/50 kV transformer, designated as T, is used, and L_m = 0.8455 H. The leakage inductance is 1.55 mH, which needs to be included in L during the numerical calculation. The value of the total capacitance in parallel with the secondary side of T is 500 pF. In practice, we should minimize the number of the components that need to be adjusted to promote efficiency and cost savings. In our test, all the parameters of the components in the primary side circuit were kept unchanged except for R₂, C₂ and L. Actually, the impulse voltage waveform can be effectively changed by adjusting R₂, C₂ and L.

Figure 15b–d shows the actual waveforms under different circuit parameter combinations. In the presence of leakage inductance with the order of millihenries, OSI waveform can be generated without L but with small damping resistance R₂. The decrease of the damping resistance and increase of L will lead to more intense oscillation of the waveform and larger IMR. Decreasing wave-tail resistor R₁ can significantly reduce T₂ within a limited range, but T₂ will not be endlessly increased by the increase in R₁, i.e., as R₁ increases, T₂ will tend to saturate. If the load capacitance C₃ is converted to the primary circuit by multiplying it with the transformer ratio, the value of equivalent capacitance C₂’ would become very large. Therefore, an insufficient value of C₁ would limit the amplitude of the output impulse and lengthen T_p. The comparison of the actual and calculated waveform parameters are listed in

Table 3. Comparisons of the actual waveform parameters and the numerical results under different circuit parameters.

Subfigure No.	Circuit Parameters						Charging Voltage	Peak Time			Half-Peak Time			Output Voltage Amplitude			Output Efficiency
	L (mH)	C1 (μF)	C2 (μF)	C3 (pF)	R1 (Ω)	R2 (Ω)	UC1 (V)	Tp (μs)	TP’ (μs)	ep (%)	T2 (μs)	T2’ (μs)	e2 (%)	Um (kV)	Um’ (kV)	em (%)	IMR
15a	1.55	10	1	500	1300	56	160	1532	1549	−1.1	6188	6272	−1.3	8.4	8.67	−3.1	52.5
15b	1.55	10	0	500	300	10	170	356	359	−0.84	3224	3442	−6.3	12.0	12.58	−4.6	70.6
15c	1.55	4.7	0	500	130	25	200	310	315	−1.6	2782	2706	2.8	8.16	8.4	−2.9	40.8
15d	1.55	4.7	0	500	1000	4	190	250	251	−0.40	2395	2391	0.18	9.84	10.5	−6.3	51.8
15e	2.9	6.8	0	500	100,000	4	200	396	401	−1.2	3500	3657	−4.3	15.0	15.7	−4.5	75
15f	4.02	6.8	0	500	1000	4	200	471	470	−0.21	3300	3402	−3.0	14.8	15.6	−5.1	74

Note: T_p, T₂ and U_m represent the actual waveform parameters; T_p’, T₂’ and U_m’ represent the calculated waveform parameters; e_p, e₂ and e_m represent error between the actual and calculated waveform parameters.

. It reveals that the influence of each component parameter of the voltage waveform is the same as that in the foregoing theoretical analysis.

It is worth noting that by using the IGBT, the impulse voltages are smoothly produced. The high-frequency oscillation that overlapped on the impulse waveform, which is attributed to the jitter of the traditional spark gap, does not exist in the IGBT-triggered impulses.

4.2. Control of Impulse Magnification Ratio

As analyzed earlier, increasing L or decreasing R₂ can relatively improve IMR in a limited range. Additionally, if the variation in the time parameters of the waveforms (T_p and T₂) is permitted in a certain range, C₁ should be chosen to be as large as possible to enhance the circuit efficiency and IMR. In general, the time parameters and IMR are considered to be a contradictory pair during the adjustment of the waveform and output level. However, our theoretical analysis indicates that decreasing the leakage inductance (L_m) and the equivalent capacitance (part of C₃) of the transformer can effectively reduce waveform parameters T_p and T₂, which may provide an effective solution to the contradiction. In other words, if the leakage inductance, winding resistance, and equivalent capacitance of the transformer are sufficiently small, waveform oscillation would be easier to produce, and the oscillation frequency would be higher; thus, T_p would be smaller. Therefore, choosing a transformer with small leakage inductance, winding resistance, and equivalent capacitance is necessary.

4.3. Error Sources

Table 3 indicates that the main differences between the parameters of the actual and calculated waveforms are T_p and T₂. The results of smaller T_p in most cases are caused by the underestimation of the leakage inductance of the transformer. T₂ is also generally smaller than T₂' when T₂ is relatively small, which may be because the resistance of the magnetizing branch of the transformer is ignored in the calculation.

Generally, the theoretical and practical studies on the technology based on IGBT triggering control and transformer induction proved that generating different types of SI voltage is possible, including SI and OSI recommended by the IEC60060-3 standard [4]. Furthermore, the waveform parameters to output a SI voltage can be easily adjusted by changing the parameters of the primaryside circuit elements.

5. Discussion

5.1. Technical Requirements in Achieving a Higher Amplitude and Larger Capacity Output Voltage

As stated earlier, to achieve higher voltage and larger capacity output of the SI voltage, two methods can be considered. One is that using a voltage doubling circuit or improving the output voltage of the voltage regulator enhances the voltage of the transformer primary side. In this case, the IGBT module is required not only to withstand the working voltage with higher amplitude for a long time but also to have a bigger energy discharge capability. The other is choosing a transformer with a greater transformation ratio. Under the circumstances, the intrinsic parameters of the transformer will also increase with the increase in the transformation ratio, which causes the output waveform to accordingly change. At this time, a T-type equivalent circuit of the transformer should be considered, instead of the Γ-type equivalent circuit. Thus, more accurate numerical analysis result of the output waveform can be obtained.

5.2. Technical Requirements in Achieving Lightning and Oscillating Lightning Impulse Voltage

By the same principle utilized in this paper, lightning impulse voltage can also be realized technically. However, the following technical issues need to be considered.

(1)

Because the peak time of the lightning impulse voltage is much smaller than that of the SI voltage, a faster switch response speed of the IGBT module is correspondingly required.

(2)

The single phase transformer, which is used to generate the lightning impulse voltage, needs to withstand the impulse voltage with a much shorter rise time. Thus, the transformer must guarantee sufficient insulating strength against damage under high impulse work condition, which is a necessary technical premise to output a lightning impulse voltage without failure.

(3)

With regard to lightning impulse voltage with smaller peak time and half-peak time, a tighter match among the circuit parameters (including the transformer parameters) should be ensured to achieve steady and controllable output. Due to the increase of the transformer working frequency, the Γ-type (or T-type) equivalent circuit of the transformer, which is originally applied to generate an SI voltage, cannot be effectively used to analyze the loop of the lightning impulse voltage. Thus, considering the winding capacitances and stray capacitances of transformer [15], a high-frequency equivalent circuit must be utilized (Figure 16). However, this model will certainly increase the complexity of the equivalent circuit of the entire system and makes the numerical analysis theory, which provides guidance in building the actual circuit, more difficult.

6. Conclusions

In this present paper, a new compact and removable SI generator based on transformer boosting was developed with IGBT control. An optimization design method was proposed by considering both of the output efficiency and waveform errors. By numerical calculation and error correction, the component parameters of the primary side of the transformer, such as the magnetic inductance, leakage inductance, winding resistance and equivalent capacitance, were determined for the target SIs. To address the synchronization problem which is usually caused by multiple spark gaps, an IGBT with drive circuit was employed as the impulse trigger. It was proven that the IGBT within the range of the forward withstand voltage can well replace the traditional sphere gap switch. The generator was finally built on a removable high voltage transformer with small size. The experiment showed that the waveform parameters of SI and OSI voltages generated by the new generator were consistent with the numerical calculation and the error estimation.